標本分散![]() は次式で求められる。この
は次式で求められる。この![]() と、母分散
と、母分散![]() の関係を導いてゆく。
の関係を導いてゆく。
(1) 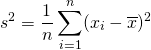
以後、![]() のパラメータを省略する。まず
のパラメータを省略する。まず![]() を母平均として、
を母平均として、![]() を以下のように変形する。
を以下のように変形する。
(2) 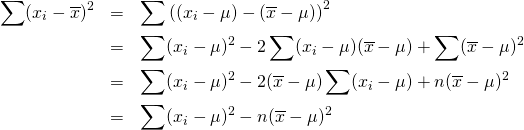
これより、標本分散![]() の期待値は以下のようになる。
の期待値は以下のようになる。
(3) 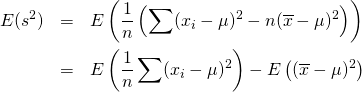
1項目については、
(4) ![]()
また第2項目は標本平均の分散より、
(5) ![]()
これらより、標本分散の期待値は以下のようになる。
(6) ![]()
式(6)より、母分散を得るために以下のように変形。
(7) ![]()
これは、左辺の()の中が母分散![]() の不偏推定量であることを示している。このことから、母分散に対する不偏分散
の不偏推定量であることを示している。このことから、母分散に対する不偏分散![]() は次式で表される。
は次式で表される。
(8) ![]()
不偏分散の分母が![]() となっているのは、母分散なら
となっているのは、母分散なら![]() となるところが、標本の計算では
となるところが、標本の計算では![]() であり、
であり、![]() が他の標本から計算されることから、変数の数(自由度)が1少ないことを表している。自由度が少なければ、目指す値を計算するデータが一つ少なくなり、ばらつきはその分大きくなる。
が他の標本から計算されることから、変数の数(自由度)が1少ないことを表している。自由度が少なければ、目指す値を計算するデータが一つ少なくなり、ばらつきはその分大きくなる。
(8)式の右辺、2乗かと.
ありがとうございます。参考になりました。