scikit-learn – LogisticRegression

2020-05-17 / tau / コメントする

概要

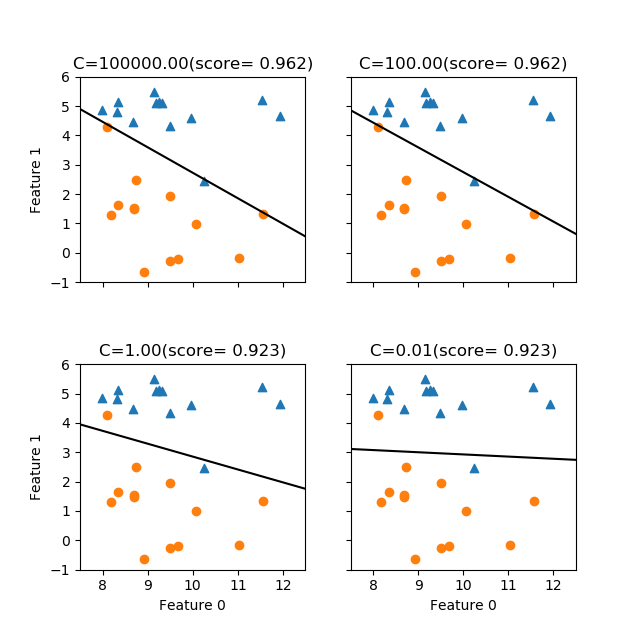
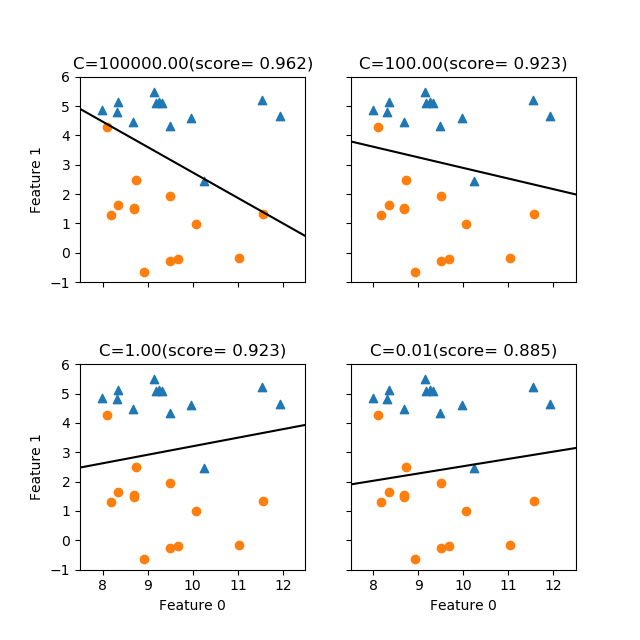
scikit-learnのLogisticRegressionモデルはLogistic回帰のモデルを提供する。利用方法の概要は以下の手順で、LinearRegressionなど他の線形モデルとほぼ同じだが、モデルインスタンス生成時に与える正則化パラメーターCはRidge/Lassoのalphaと逆で、正則化の効果を強くするにはCを小さくする（Cを大きくすると正則化が弱まり、訓練データに対する精度は高まるが過学習の可能性が高くなる）。

また、正則化の方法をL1正則化、L2正則化、Elastic netから選択できる。

LogisticRegressのクラスをインポートする
ハイパーパラメーターC、正則化方法、solver（収束計算方法）などを指定し、モデルのインスタンスを生成する
fit()メソッドに訓練データを与えて学習させる

学習済みのモデルの利用方法は以下の通り。

score()メソッドにテストデータを与えて適合度を計算する
predict()メソッドに説明変数を与えてターゲットを予測
モデルインスタンスのプロパティーからモデルのパラメーターを利用
- 切片はintercept_、重み係数はcoef_(末尾のアンダースコアに注意)

利用例

以下は、breast_cancerデータセットに対してLogisticRegressionを適用した例。デフォルトのsolverは'lbfgs'でデフォルトの最大収束回数(100)では収束しなかったため、max_iter=3000を指定している。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression(max_iter=3000).fit(X_train, y_train)
print("")
print("Training score: {}".format(logreg.score(X_train, y_train)))
print("Test score    : {}".format(logreg.score(X_test, y_test)))
print("Prediction")
for i in range(3):
    print("{} -> {}".format(y_test[i], logreg.predict(X_test[i].reshape(1, -1))))

# Training score: 0.9577464788732394
# Test score    : 0.958041958041958
# Prediction
# 1 -> [1]
# 0 -> [0]
# 1 -> [1]

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression(max_iter=3000).fit(X_train, y_train)

print("")

print("Training score: {}".format(logreg.score(X_train, y_train)))

print("Test score : {}".format(logreg.score(X_test, y_test)))

print("Prediction")

for i in range(3):

print("{} -> {}".format(y_test[i], logreg.predict(X_test[i].reshape(1, -1))))

# Training score: 0.9577464788732394

# Test score : 0.958041958041958

# Prediction

# 1 -> [1]

# 0 -> [0]

# 1 -> [1]

利用方法

LogisticRgressionの主な利用方法はLineaRegressionとほとんど同じで、以下は特有の設定を中心にまとめる。

モデルクラスのインポート

scikit-learn.linear_modelパッケージからLogisticRegressonクラスをインポートする。

from sklearn.linear_model import LogisticRegression

1	from sklearn.linear_model import LogisticRegression

モデルのインスタンスの生成

LogisticRegressionでは、ハイパーパラメーターCによって正則化の強さを指定する。このCはRidge/Lassoのalphaと異なり、正則化の効果を強めるためには値を小さくする。デフォルトはC=1.0。

logreg = LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0,
             fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,
             solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False,
             n_jobs=None, l1_ratio=None)

logreg = LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0,

fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,

solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False,

n_jobs=None, l1_ratio=None)

以下、RidgeとLassoに特有のパラメーターのみ説明。LinearRegressionと共通のパラメーターはLinearRegressionを参照。

penalty: 'l1', 'l2', 'elasticnet', 'none'で正則化項のノルムのタイプを指定する。ソルバーの'newton-cg','sag','lbfgs'はL2正則化のみサポートし、'elasticnet'は'saga'のみがサポートする。デフォルトは'none'で正則化は適用されない('liblinear'は'none'に対応しない)。
tol: 収束計算の解の精度で、デフォルトは1e-4。
C: 正則化の強さの逆数。正の整数で指定し、デフォルトは1.0。
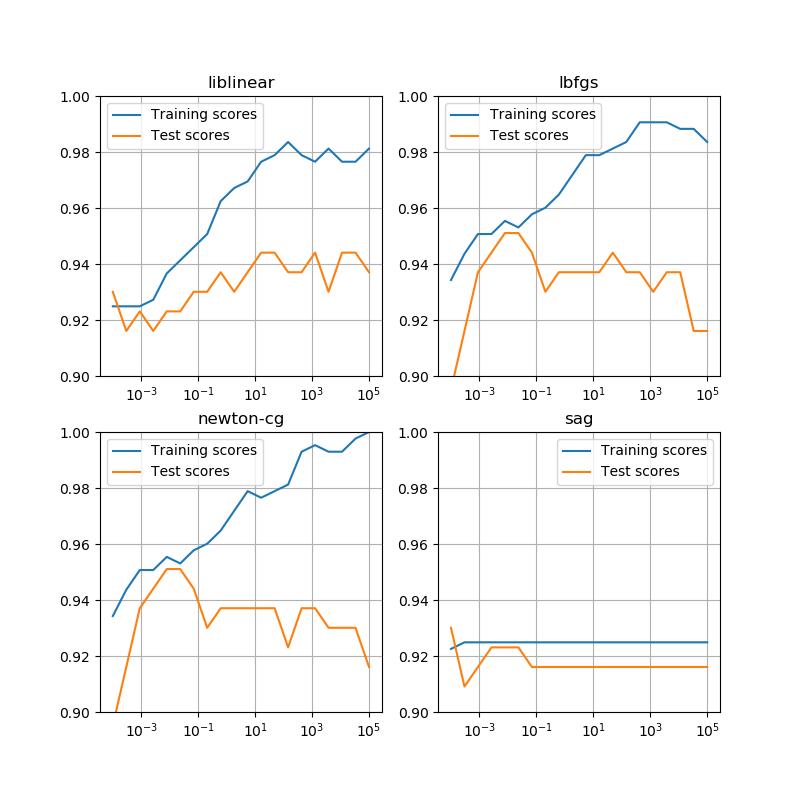
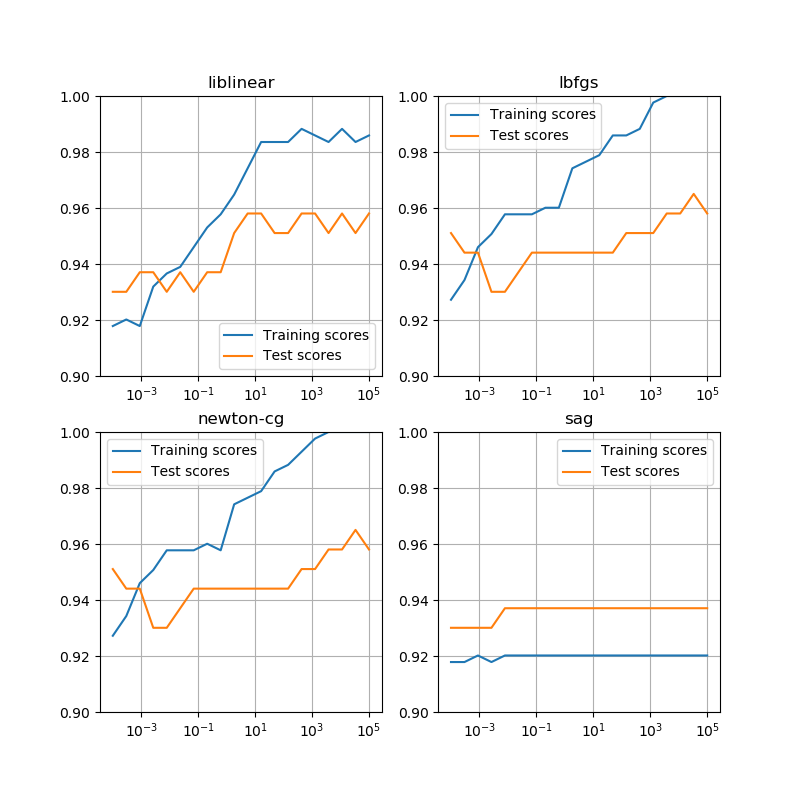
solver: 'newton-cg'、'lbfgs'、'liblinear'、'sag'、'saga'のうちから選択される。デフォルトは'lbfgs'。小さなデータセットには'liblnear'が適し、大きなデータセットに対しては'sag'、'saga'の計算が速い。複数クラスの問題には、'newton-cg'、'sag'、'saga'、'lbfgs'が対応し、'liblinear'は一対他しか対応しない。その他ノルムの種類とソルバーの対応。
max_iter: 収束計算の制限回数を指定する。デフォルト値は100。
random_state: データをシャッフルする際のランダム・シードで、solver='sag'の際に用いる。
l1_ratio: Elastic-Netのパラメーター。[0, 1]の値で、penalty='elasticnet'の時のみ使われる。

モデルの学習

fit()メソッドに特徴量とターゲットの訓練データを与えてモデルに学習させる(回帰係数を決定する)。

lr.fit(X, y)

1	lr.fit(X, y)

X: 特徴量の配列。2次元配列で、各列が各々の説明変数に対応し、行数はデータ数を想定している。変数が1つで1次元配列の時はreshape(-1, 1)かスライス([:, n:n+1])を使って1列の列ベクトルに変換する必要がある。
y: ターゲットの配列で、通常は1変数で1次元配列。

3つ目の引数sample_weightは省略。

適合度の計算

score()メソッドに特徴量とターゲットを与えて適合度を計算する。

lr.score(X, y)

1	lr.score(X, y)

その他のメソッド

decision_function(X)
densiffy()
predict_proba(X)
predict_log_proba()
sparsify()

Logistic回帰～forgeデータ～Pythonではじめる機械学習より

2020-05-17 / tau / コメントする

概要

O’REILLYの書籍”Pythonではじめる機械学習”の2.3.3.5、Logistic回帰でforgeデータの決定境界をトレースしてみたとき、収束計算のソルバーの違いや、元データと書籍のデータの違いなどから再現性に悩んだので記録しておく。

決定境界

mglearnのforgeデータセットに対してLogisticRegressionを適用してみる。

Cがかなり大きい場合、すなわち正則をほとんど行わない場合には、与えられたデータに対して可能な限り適合させようとしており、データに対する適合度は高い。Cが小さくなると正則化が効いてきて、データ全体に対して適合させようとしているように見える。

ここで上の図のC=1のケースは、書籍の図2-15右側と比べると決定境界の勾配が逆になっている。その理由は次のようであることが分かった。

書籍ではLogisticRegression()の収束手法を指定せず、デフォルトのsolver='liblinear'が使用されている
今回指定なしで実行したところ、以下のような警告が発生
- FutureWarning: Default solver will be changed to ‘lbfgs’ in 0.22. Specify a solver to silence this warning.
  FutureWarning)
- デフォルトのソルバーが（現在はliblinearだが）ver 0.22ではlbfgsになる／このwarningを黙らせるためにソルバーを指定せよ
そこでモデルのインスタンス生成時にLogisticRegression(solver='lbfgs')としたところ先の結果となった
指定なし、あるいはsolver='liblinear'とすると書籍と同じ結果になる

liblinearによる結果が以下の通り。正則化の度合いに応じてlbfgsよりも傾きがダイナミックに変わっているように見える。

なお、これらの図の傾きについて、今度は書籍の図2-16と随分違っている。よく見てみると、同図のforgeデータは特に下側の〇印の点でオリジナルにはないデータがいくつか加わっているためと考えられる。

これらのコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
from mglearn.datasets import make_forge
from sklearn.linear_model import LogisticRegression

X, y = make_forge()

xmin, xmax = 7.5, 12.5
ymin, ymax = -1, 6

C_values = [1e5, 1e2, 1e0, 1e-2]

fig, axs = plt.subplots(2, 2, figsize=(6.4, 6.4))
fig.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -1)

for ax, c in zip(axs_1d[0], C_values):
    logreg = LogisticRegression(C=c, solver='liblinear')
    logreg.fit(X, y)

    b = logreg.intercept_[0]
    w0 = logreg.coef_[0][0]
    w1 = logreg.coef_[0][1]

    x_border = np.linspace(xmin, xmax)
    y_border = (-b - w0 * x_border) / w1

    ax.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='^')
    ax.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='o')

    ax.plot(x_border, y_border, 'k')

    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)

    ax.set_title("C={:2.2f}(score={:6.3f})".format(c, logreg.score(X, y)))
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")
    ax.label_outer()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mglearn.datasets import make_forge

from sklearn.linear_model import LogisticRegression

X, y = make_forge()

xmin, xmax = 7.5, 12.5

ymin, ymax = -1, 6

C_values = [1e5, 1e2, 1e0, 1e-2]

fig, axs = plt.subplots(2, 2, figsize=(6.4, 6.4))

fig.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -1)

for ax, c in zip(axs_1d[0], C_values):

logreg = LogisticRegression(C=c, solver='liblinear')

logreg.fit(X, y)

b = logreg.intercept_[0]

w0 = logreg.coef_[0][0]

w1 = logreg.coef_[0][1]

x_border = np.linspace(xmin, xmax)

y_border = (-b - w0 * x_border) / w1

ax.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='^')

ax.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='o')

ax.plot(x_border, y_border, 'k')

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_title("C={:2.2f}(score={:6.3f})".format(c, logreg.score(X, y)))

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

ax.label_outer()

plt.show()

3次元表示

2つのCの値について、二つの特徴量の組み合わせに対する青い点の確率分布を表示してみる(solver='lbfgs')。Cが小さいと確率分布がなだらかになる様子が見て取れるが、データに対する判別の適合度との関係はよくわからない。

import numpy as np
import matplotlib.pyplot as plt
from mglearn.datasets import make_forge
from sklearn.linear_model import LogisticRegression
from mpl_toolkits.mplot3d import Axes3D

X, y = make_forge()

xmin, xmax = 7.5, 12.5
ymin, ymax = -1, 6

gx = np.linspace(xmin, xmax, 40)
gy = np.linspace(ymin, ymax, 40)
gx, gy = np.meshgrid(gx, gy)

C_values = [1e3, 1e-1]

fig = plt.figure(figsize=(12, 4.8))

ax0 = fig.add_subplot(121, projection='3d')
ax1 = fig.add_subplot(122, projection='3d')
axs = [ax0, ax1]

for ax, c in zip(axs, C_values):
    logreg = LogisticRegression(C=c, solver='lbfgs')
    logreg.fit(X, y)

    b = logreg.intercept_[0]
    w0 = logreg.coef_[0][0]
    w1 = logreg.coef_[0][1]
    gz = 1/(1 + np.exp(-b - w0*gx - w1*gy))
    gz05 = np.full_like(gz, 0.5)

    y_border_min = (-b - w0 * xmin) / w1
    y_border_max = (-b - w0 * xmax) / w1

    ax.scatter(X[:, 0][y==1], X[:, 1][y==1], 0.5, color='tab:blue')
    ax.scatter(X[:, 0][y==0], X[:, 1][y==0], 0.5, color='tab:red')
    ax.plot_wireframe(gx, gy, gz, color='tab:green', alpha=0.5)
    ax.plot_surface(gx, gy, gz05, color='k', alpha=0.2)
    ax.plot([xmin, xmax], [y_border_min, y_border_max], 0.5)

    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)

    ax.set_title("C={}".format(c))
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mglearn.datasets import make_forge

from sklearn.linear_model import LogisticRegression

from mpl_toolkits.mplot3d import Axes3D

X, y = make_forge()

xmin, xmax = 7.5, 12.5

ymin, ymax = -1, 6

gx = np.linspace(xmin, xmax, 40)

gy = np.linspace(ymin, ymax, 40)

gx, gy = np.meshgrid(gx, gy)

C_values = [1e3, 1e-1]

fig = plt.figure(figsize=(12, 4.8))

ax0 = fig.add_subplot(121, projection='3d')

ax1 = fig.add_subplot(122, projection='3d')

axs = [ax0, ax1]

for ax, c in zip(axs, C_values):

logreg = LogisticRegression(C=c, solver='lbfgs')

logreg.fit(X, y)

b = logreg.intercept_[0]

w0 = logreg.coef_[0][0]

w1 = logreg.coef_[0][1]

gz = 1/(1 + np.exp(-b - w0*gx - w1*gy))

gz05 = np.full_like(gz, 0.5)

y_border_min = (-b - w0 * xmin) / w1

y_border_max = (-b - w0 * xmax) / w1

ax.scatter(X[:, 0][y==1], X[:, 1][y==1], 0.5, color='tab:blue')

ax.scatter(X[:, 0][y==0], X[:, 1][y==0], 0.5, color='tab:red')

ax.plot_wireframe(gx, gy, gz, color='tab:green', alpha=0.5)

ax.plot_surface(gx, gy, gz05, color='k', alpha=0.2)

ax.plot([xmin, xmax], [y_border_min, y_border_max], 0.5)

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_title("C={}".format(c))

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

plt.show()

scikit-learn – LinearRegression

2020-05-10 / tau / コメントする

概要

scikit-learnのLinearRegressionは、最も単純な多重線形回帰モデルを提供する。

モデルの利用方法の概要は以下の手順。

LinearRegressionのクラスをインポートする
モデルのインスタンスを生成する
fit()メソッドに訓練データを与えて学習させる

学習済みのモデルの利用方法は以下の通り。

score()メソッドにテストデータを与えて適合度を計算する
predict()メソッドに説明変数を与えてターゲットを予測
モデルインスタンスのプロパティーからモデルのパラメーターを利用
- 切片はintercept_、重み係数はcoef_(末尾のアンダースコアに注意)

利用例

配列による場合

以下はscikit-learnのBoston hose pricesデータのうち、2つの特徴量RM(1戸あたり部屋数)とLSTAT(下位層の人口比率)を取り出して、線形回帰のモデルを適用している。

特徴量の一部をとりだすのに、ファンシー・インデックスでリストの要素に2つの変数のインデックスを指定している。また、特徴量データXとターゲットデータyをtrain_test_split()を使って訓練データとテストデータに分けている。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

ds = load_boston()

X = ds.data[:, [5, 12]]
y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))
print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343
# Prediction for (7, 5):[31.14766768]
# Intercept:-0.6047107435077521
# Coefficients:[ 5.01785312 -0.67451869]

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

ds = load_boston()

X = ds.data[:, [5, 12]]

y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))

print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343

# Prediction for (7, 5):[31.14766768]

# Intercept:-0.6047107435077521

# Coefficients:[ 5.01785312 -0.67451869]

DataFrameによる場合

以下の例では、データセットの本体(data)をpandasのDataFrameとして構成し、2つの特徴量RMとLSTATを指定して取り出している。

import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

ds = load_boston()
df = pd.DataFrame(ds.data, columns=ds.feature_names)

X = df[['RM', 'LSTAT']]
y = ds['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))
print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343
# Prediction for (7, 5):[31.14766768]
# Intercept:-0.6047107435077521
# Coefficients:[ 5.01785312 -0.67451869]

import pandas as pd

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

ds = load_boston()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X = df[['RM', 'LSTAT']]

y = ds['target']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))

print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343

# Prediction for (7, 5):[31.14766768]

# Intercept:-0.6047107435077521

# Coefficients:[ 5.01785312 -0.67451869]

利用方法

モデルクラスのインポート

scikit-learn.linear_modelパッケージからLinearRegressionクラスをインポートする。

from sklearn.linear_model import LinearRegression

1	from sklearn.linear_model import LinearRegression

モデルのインスタンスの生成

LinearRegressionの場合、ハイパーパラメーターの指定はない。

lr = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

1	lr = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

fit_intercept: 切片を計算しない場合Falseを指定。デフォルトはTrueで切片も計算されるが、原点を通るべき場合にはFalseを指定する。
normalize: Trueを指定すると、特徴量Xが学習の前に正規化(normalize)される(平均を引いてL2ノルムで割る)。デフォルトはFalse。fit_intercept=Falseにセットされた場合は無視される。説明変数を標準化(standardize)する場合はこの引数をFalseにしてsklearn.preprocessing.StandardScalerを使う。
copy_X: Trueを指定するとXはコピーされ、Falseの場合は上書きされる。デフォルトはTrue。
n_jobs: 計算のジョブの数を指定する。デフォルトはNoneで1に相当。n_targets > 1のときのみ適用される。

モデルの学習

fit()メソッドに特徴量とターゲットの訓練データを与えてモデルに学習させる(回帰係数を決定する)。

lr.fit(X, y)

1	lr.fit(X, y)

X: 特徴量の配列。2次元配列で、各列が各々の説明変数に対応し、行数はデータ数を想定している。変数が1つで1次元配列の時はreshape(-1, 1)かスライス([:, n:n+1])を使って1列の列ベクトルに変換する必要がある。
y: ターゲットの配列で、通常は1変数で1次元配列。

3つ目の引数sample_weightは省略。

適合度の計算

score()メソッドに特徴量とターゲットを与えて適合度を計算する。

lr.score(X, y)

1	lr.score(X, y)

戻り値は適合度を示す実数で、回帰計算の決定係数R²で計算される。

(1) $\begin{equation*} R^2 = 1 - \frac{RSS}{TSS} = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \overline{y})^2} \end{equation*}$

モデルによる予測

predict()メソッドに特徴量を与えて、ターゲットの予測結果を得る。

y_pred = lr.predict(X)

1	y_pred = lr.predict(X)

ここで特徴量Xは複数のデータセットの2次元配列を想定しており、1組のデータの場合でも2次元配列とする必要がある。

y_pred = lr.pred([[x1, x2,..., xm]])

1	y_pred = lr.pred([[x1, x2,..., xm]])

また、結果は複数のデータセットに対する1次元配列で返されるため、ターゲットが1つの場合でも要素数1の1次元配列となる。

切片・係数の利用

fit()メソッドによる学習後、モデルの学習結果として切片と特徴量に対する重み係数を得ることができる。

各々モデル・インスタンスのプロパティーとして保持されており、切片はintercept_で1つの実数、重み係数はcoeff_で特徴量の数と同じ要素数の1次元配列となる(特徴量が1つの場合も要素数1の1次元配列)。

ic = lr.intercept_
cf = lr.coef_

1 2	ic = lr.intercept_ cf = lr.coef_

末尾のアンダースコアに注意。

実行例

waveデータセットに対する単回帰

ndarray – 行・列の抽出

2020-05-09 / tau / コメントする

例示用の配列

以下の配列を例示用に準備する。

import numpy as np

a = np.arange(30).reshape(6, 5)
print(a)

# [[ 0  1  2  3  4]
#  [ 5  6  7  8  9]
#  [10 11 12 13 14]
#  [15 16 17 18 19]
#  [20 21 22 23 24]
#  [25 26 27 28 29]]

import numpy as np

a = np.arange(30).reshape(6, 5)

print(a)

# [[ 0 1 2 3 4]

# [ 5 6 7 8 9]

# [10 11 12 13 14]

# [15 16 17 18 19]

# [20 21 22 23 24]

# [25 26 27 28 29]]

単一の行・列の抽出

単一の行の抽出

単に1つ目のインデックスを指定すると、それに対応する行が抽出される。2つ目の引数を省略すると、全て':'を指定したことになる。

print(a[3])

# [15 16 17 18 19]

print(a[3])

# [15 16 17 18 19]

単一の列の抽出

1つ目の引数を':'とし、2つ目にインデックスを指定すると、対応する列が抽出される。ただし結果は1次元の配列となる。

print(a[:, 2])

# [ 2  7 12 17 22 27]

print(a[:, 2])

# [ 2 7 12 17 22 27]

これを列ベクトルとして取り出すのに2つの方法がある。

1つ目の方法はreshape(-1, 1)とする定石。2つ目の引数1は列数1を指定し、1つ目の引数を−1にすることで、列数とサイズから適切な行数が設定される。

print(a[:, 2].reshape(-1, 1))

# [[ 2]
#  [ 7]
#  [12]
#  [17]
#  [22]
#  [27]]

print(a[:, 2].reshape(-1, 1))

# [[ 2]

# [ 7]

# [12]

# [17]

# [22]

# [27]]

2つ目の方法は、列数を指定するのに敢えて1列のスライスで指定する方法。後述するように、列をスライスで指定した場合は2次元の形状が保持されることを利用している。以下の例では、2列目から2列目までの「範囲」を指定している。

print(a[:, 2:3])

# [[ 2]
#  [ 7]
#  [12]
#  [17]
#  [22]
#  [27]]

print(a[:, 2:3])

# [[ 2]

# [ 7]

# [12]

# [17]

# [22]

# [27]]

連続する複数の行・列の抽出

連続する複数行の抽出

1つ目の引数をスライスで指定して、連続する複数行を抽出。

print(a[2:5])

# [[10 11 12 13 14]
#  [15 16 17 18 19]
#  [20 21 22 23 24]]

print(a[2:5])

# [[10 11 12 13 14]

# [15 16 17 18 19]

# [20 21 22 23 24]]

連続する複数列の抽出

2つ目の引数をスライスで指定して、連続する複数列を抽出。

print(a[:, 1:4])

# [[ 1  2  3]
#  [ 6  7  8]
#  [11 12 13]
#  [16 17 18]
#  [21 22 23]
#  [26 27 28]]

print(a[:, 1:4])

# [[ 1 2 3]

# [ 6 7 8]

# [11 12 13]

# [16 17 18]

# [21 22 23]

# [26 27 28]]

不連続な複数の行・列を抽出

不連続な複数の行を抽出

第1引数をリストで指定すると、その要素をインデックスとする複数の行が抽出される。このような指定方法のインデックスを、ファンシーインデックスと言う。

print(a[[2, 4]])

# [[10 11 12 13 14]
#  [20 21 22 23 24]]

print(a[[2, 4]])

# [[10 11 12 13 14]

# [20 21 22 23 24]]

リストの要素は昇順である必要はなく、要素順に行が取り出される。

print(a[[4, 2]])

# [[20 21 22 23 24]
#  [10 11 12 13 14]]

print(a[[4, 2]])

# [[20 21 22 23 24]

# [10 11 12 13 14]]

不連続な複数の列の抽出

1つ目の引数を':'とし、2つ目の引数をリストで指定して要素に対応する列を取り出せる。

print(a[:, [1, 3]])

# [[ 1  3]
#  [ 6  8]
#  [11 13]
#  [16 18]
#  [21 23]
#  [26 28]]

print(a[:, [1, 3]])

# [[ 1 3]

# [ 6 8]

# [11 13]

# [16 18]

# [21 23]

# [26 28]]

列についても、要素の順番は任意。

print(a[:, [3, 1]])

# [[ 3  1]
#  [ 8  6]
#  [13 11]
#  [18 16]
#  [23 21]
#  [28 26]]

print(a[:, [3, 1]])

# [[ 3 1]

# [ 8 6]

# [13 11]

# [18 16]

# [23 21]

# [28 26]]

matplotlib.patches – 図形の描画

2020-04-30 / tau / コメントする

概要

matplotlib.patchesパッケージに様々な図形クラスが準備されていて、Axesのadd_patch()メソッドでそれらのオブジェクトを加えていく。

import matplotlib.pyplot as plt
import matplotlib.patches as patch

fig, ax = plt.subplots()

circ = patch.Circle(xy=(3, 3), radius=2, ec='b', fc='gray')
elli = patch.Ellipse(xy=(2, 1), width=2, height=1, ec='g', fill=False, angle=10)
rect = patch.Rectangle(xy=(1, 2), width=3, height=2, ec='b', fc='w', angle=30)

ax.add_patch(circ)
ax.add_patch(elli)
ax.add_patch(rect)

ax.set_xlim(0, 6)
ax.set_ylim(0, 6)
ax.set_aspect('equal')

plt.show()

import matplotlib.pyplot as plt

import matplotlib.patches as patch

fig, ax = plt.subplots()

circ = patch.Circle(xy=(3, 3), radius=2, ec='b', fc='gray')

elli = patch.Ellipse(xy=(2, 1), width=2, height=1, ec='g', fill=False, angle=10)

rect = patch.Rectangle(xy=(1, 2), width=3, height=2, ec='b', fc='w', angle=30)

ax.add_patch(circ)

ax.add_patch(elli)

ax.add_patch(rect)

ax.set_xlim(0, 6)

ax.set_ylim(0, 6)

ax.set_aspect('equal')

plt.show()

各種図形

以下の点は各図形において共通

ほとんどの図形は引数xyで基準点のx座標とy座標をタプルで与える
edgecolor/ecで外枠の色、facecolor/fcで塗りつぶし色を指定する
fill=True/Falseで塗りつぶしの有無を指定する
angleで傾きの角度を指定できる図形がある

Circle(xy[, radius=5]): 中心点を指定して円を描く。
Ellipse(xy, width, height[, angle]): 中心点と幅・高さを指定して楕円を描く。
Rectangle(xy, width, height[, angle]): 左下の点と幅・高さを指定して楕円を描く。
CirclePolygon(x, y, rasius=5, resolution=20): 多角形を描画。辺／頂点の数をresolutionで指定する。
Polygon(xy, closed=True): 複数の点を指定して図形を描画する。xyはNx2配列(xy座標を要素とした2次元配列)。closedをFalseに指定すると図形の最初の点と最後の点を結ばない。
Arc(xy, width, height[, angle, theta1, theta2]): 楕円の一部の弧を描く。扇形に中を塗りつぶすことはできない。
Wedge(center, r, theta1, theta2[, width=None]): 円の一部を切出した図形を描く。widhを指定すると中心からその長さだけ除かれて描かれる。

Arrow(x, y, dx, dy[, width, ...]): 矢印を描画する。
FancyArrow(x, y, dx, dy[, width, ...]): 鏃を片側だけにしたり、鏃の大きさや形を設定したりできる。

waveデータセット – 線形回帰

2020-04-05 / tau / コメントする

O’Reillyの”Pythonではじめる機械学習”に載っている、scikit-learnの線形回帰のwaveデータセットへの適用の再現。

waveデータセットのサンプル数を60、train_test_split()でrandom_satet=42として、書籍と同じグラフを得る。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from mglearn.datasets import make_wave

xmin, xmax = -3, 3
ymin, ymax = -3, 3

X_source, y_source = make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X_source, y_source, random_state=42)

linreg = LinearRegression()
linreg.fit(X_train, y_train)

X_test = np.linspace(xmin, xmax, 2).reshape(-1, 1)
y_test = linreg.predict(X_test)

print(linreg.coef_[0], linreg.intercept_)

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(X_source, y_source, s=20)
ax.plot(X_test, y_test, c="tab:orange")

ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.grid()

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from mglearn.datasets import make_wave

xmin, xmax = -3, 3

ymin, ymax = -3, 3

X_source, y_source = make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X_source, y_source, random_state=42)

linreg = LinearRegression()

linreg.fit(X_train, y_train)

X_test = np.linspace(xmin, xmax, 2).reshape(-1, 1)

y_test = linreg.predict(X_test)

print(linreg.coef_[0], linreg.intercept_)

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(X_source, y_source, s=20)

ax.plot(X_test, y_test, c="tab:orange")

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.grid()

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_aspect('equal')

plt.show()

また、訓練結果の係数、切片とスコアについても同じ結果を得ることができる。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from mglearn.datasets import make_wave

X, y = make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

linreg = LinearRegression()
linreg.fit(X_train, y_train)

print("coef_     : {}".format(linreg.coef_))
print("intercept_: {}".format(linreg.intercept_))

print("training score: {:.3f}".format(linreg.score(X_train, y_train)))
print("test score    : {:.3f}".format(linreg.score(X_test, y_test)))

# coef_     : [0.39390555]
# intercept_: -0.031804343026759746
# training score: 0.670
# test score    : 0.659

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from mglearn.datasets import make_wave

X, y = make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

linreg = LinearRegression()

linreg.fit(X_train, y_train)

print("coef_ : {}".format(linreg.coef_))

print("intercept_: {}".format(linreg.intercept_))

print("training score: {:.3f}".format(linreg.score(X_train, y_train)))

print("test score : {:.3f}".format(linreg.score(X_test, y_test)))

# coef_ : [0.39390555]

# intercept_: -0.031804343026759746

# training score: 0.670

# test score : 0.659

Breast cancer データセット – Logistic回帰による学習率曲線

2020-04-05 / tau / コメントする

概要

breast-cancerデータセットにscikit-learnのLogisticRegressionクラスでLogistic回帰を適用した結果。

手法全般の適用の流れはLogistic回帰～cancer～Pythonではじめる機械学習よりを参照。

ここではハイパーパラメーターを変化させたときの学習率の違いをみている。

学習率曲線

scikit-learnのLogisticRegressionクラスで、正則化のパラメーターを変化させたときの学習率曲線。同クラスにはsolver引数で収束計算のいくつかの手法が選択できるが、収束手法の違いによって意外に学習率曲線に違いが出た。またtrain_test_split()のrandom_stateを変えても違いがある。569のデータセットで訓練データとテストデータを分けてもいるが、その程度では結構ばらつきが出るということかもしれない。

まず、random_state=0とした場合の、4つの収束手法における学習率曲線を示す。L-BFGSは準ニュートン法の1つらしいので、Newton-CGと同じ傾向であるのは頷ける。SAG(Stochastic Average Gradient)はまた違った計算方法のようで、他の手法と随分挙動が異なる。収束回数はmax_iter=10000で設定していて、これくらいでも計算回数オーバーの警告がいくつか出る。回数をこれより2オーダー多くしても、状況はあまり変わらない。

random_state=11としてみると、liblinearでは大きく違わないが、他の3つの手法では傾向が違っていて、特にsagを用いた場合は訓練データの学習率の方がテストデータの学習率よりも低くなっている。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer

ds = load_breast_cancer()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X_train, X_test, y_train, y_test = \
    train_test_split(df, ds.target, stratify=ds.target, random_state=0)

C_sup = np.linspace(5, -4, 20)
C_val = 10**C_sup

solvers = ['liblinear', 'lbfgs', 'newton-cg', 'sag']


fig, axs = plt.subplots(2, 2, figsize=(8, 8))
axs_1d = axs.reshape(-1)

for ax, solver in zip(axs_1d, solvers):
    train_scores = np.empty(0)
    test_scores = np.empty(0)
    for C in C_val:
        logreg = LogisticRegression(C=C, solver=solver, max_iter=10000)
        logreg.fit(X_train, y_train)
        train_scores = np.append(train_scores, logreg.score(X_train, y_train))
        test_scores = np.append(test_scores, logreg.score(X_test, y_test))

    ax.plot(C_val, train_scores, label="Training scores")
    ax.plot(C_val, test_scores, label="Test scores")

    ax.set_xscale('log')
    ax.set_ylim(0.9, 1)
    ax.grid(True)
    ax.legend()
    ax.set_title(solver)

plt.show()

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

from sklearn.datasets import load_breast_cancer

ds = load_breast_cancer()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X_train, X_test, y_train, y_test = \

train_test_split(df, ds.target, stratify=ds.target, random_state=0)

C_sup = np.linspace(5, -4, 20)

C_val = 10**C_sup

solvers = ['liblinear', 'lbfgs', 'newton-cg', 'sag']

fig, axs = plt.subplots(2, 2, figsize=(8, 8))

axs_1d = axs.reshape(-1)

for ax, solver in zip(axs_1d, solvers):

train_scores = np.empty(0)

test_scores = np.empty(0)

for C in C_val:

logreg = LogisticRegression(C=C, solver=solver, max_iter=10000)

logreg.fit(X_train, y_train)

train_scores = np.append(train_scores, logreg.score(X_train, y_train))

test_scores = np.append(test_scores, logreg.score(X_test, y_test))

ax.plot(C_val, train_scores, label="Training scores")

ax.plot(C_val, test_scores, label="Test scores")

ax.set_xscale('log')

ax.set_ylim(0.9, 1)

ax.grid(True)

ax.legend()

ax.set_title(solver)

plt.show()

ndarray.reshape – 配列の形状変更

2020-04-05 / tau / コメントする

基本

配列の形状変更は、reshape()メソッドで行う。reshape()メソッドは、元の配列を破壊せず新たな配列を生成する。

具体のいろいろな使い方は、ndarray.reshapeの使い方を参照

以下の例では6個の要素の1次元配列を2×3の2次元配列に変更し、それをさらに3 ×2の2次元配列に変更している。要素は常に行を上から、各行の列要素を左からネストした形で埋めていく。

import numpy as np

a = np.arange(6)
b = a.reshape(2, 3)
c = b.reshape(3, 2)
print(a)
print(b)
print(c)

# [0 1 2 3 4 5]
# [[0 1 2]
#  [3 4 5]]
# [[0 1]
#  [2 3]
#  [4 5]]

import numpy as np

a = np.arange(6)

b = a.reshape(2, 3)

c = b.reshape(3, 2)

print(a)

print(b)

print(c)

# [0 1 2 3 4 5]

# [[0 1 2]

# [3 4 5]]

# [[0 1]

# [2 3]

# [4 5]]

暗黙指定

サイズ変更の際、ある次元の要素数を-1とすると、他の要素数に合わせて適切に設定してくれる。

以下の例では2×3×2の3次元配列をつくり、それを3×2×2に変形しているが、2次元目を-1として1次元目と3次元目から設定させている。

import numpy as np

a1 = np.arange(10, 16).reshape(3, 2)
a2 = np.arange(20, 26).reshape(3, 2)
b = np.array([a1, a2])
print(b.ndim, b.shape)
print(b)

c = b.reshape(3, -1, 2)
print(c)

# 3 (2, 3, 2)
# [[[10 11]
#   [12 13]
#   [14 15]]
# 
#  [[20 21]
#   [22 23]
#   [24 25]]]
# [[[10 11]
#   [12 13]]
# 
#  [[14 15]
#   [20 21]]
# 
#  [[22 23]
#   [24 25]]]

import numpy as np

a1 = np.arange(10, 16).reshape(3, 2)

a2 = np.arange(20, 26).reshape(3, 2)

b = np.array([a1, a2])

print(b.ndim, b.shape)

print(b)

c = b.reshape(3, -1, 2)

print(c)

# 3 (2, 3, 2)

# [[[10 11]

# [12 13]

# [14 15]]

# [[20 21]

# [22 23]

# [24 25]]]

# [[[10 11]

# [12 13]]

# [[14 15]

# [20 21]]

# [[22 23]

# [24 25]]]

この方法は、たとえば行ベクトルの配列を列ベクトルに変換するときに使われる。以下の例では1次元の配列をつくり、それを列ベクトルとするのに、列数を1で固定し、行数を-1として算出させている。

import numpy as np

a = np.arange(3)
b = a.reshape(-1, 1)
print(b)

# [[0]
#  [1]
#  [2]]

import numpy as np

a = np.arange(3)

b = a.reshape(-1, 1)

print(b)

# [[0]

# [1]

# [2]]

1次元化するときの注意

多次元配列や列ベクトルを1次元化するとき、行数を1、列数を-1で暗黙指定すると求める1次元配列を1つだけ含む2次元の配列になる。こうなってしまのはreshape()の引数で1行×n列の2次元で指定したため。

import numpy as np

a = np.arange(12).reshape(2, 3, 2)
print(a)
print(a.reshape(1, -1))

# [[[ 0  1]
#   [ 2  3]
#   [ 4  5]]
# 
#  [[ 6  7]
#   [ 8  9]
#   [10 11]]]
# [[ 0  1  2  3  4  5  6  7  8  9 10 11]]

b = np.arange(3).reshape(-1, 1)
print(b)
print(b.reshape(1, -1))

# [[0]
#  [1]
#  [2]]
# [[0 1 2]]

import numpy as np

a = np.arange(12).reshape(2, 3, 2)

print(a)

print(a.reshape(1, -1))

# [[[ 0 1]

# [ 2 3]

# [ 4 5]]

# [[ 6 7]

# [ 8 9]

# [10 11]]]

# [[ 0 1 2 3 4 5 6 7 8 9 10 11]]

b = np.arange(3).reshape(-1, 1)

print(b)

print(b.reshape(1, -1))

# [[0]

# [1]

# [2]]

# [[0 1 2]]

そこで、size属性で1つの整数だけを指定すると、1次元でその要素数の配列になってくれる。

import numpy as np

a = np.arange(12).reshape(2, 3, 2)
print(a.reshape(a.size))

b = np.arange(3).reshape(-1, 1)
print(b.reshape(b.size))

# [ 0  1  2  3  4  5  6  7  8  9 10 11]
# [0 1 2]

import numpy as np

a = np.arange(12).reshape(2, 3, 2)

print(a.reshape(a.size))

b = np.arange(3).reshape(-1, 1)

print(b.reshape(b.size))

# [ 0 1 2 3 4 5 6 7 8 9 10 11]

# [0 1 2]

さらには、引数を-1のみで指定すると、配列のサイズを適当に持ってきて適用してくれる。

import numpy as np

a = np.arange(12).reshape(2, 3, 2)
print(a.reshape(-1))

b = np.arange(3).reshape(-1, 1)
print(b.reshape(-1))

# [ 0  1  2  3  4  5  6  7  8  9 10 11]
# [0 1 2]

import numpy as np

a = np.arange(12).reshape(2, 3, 2)

print(a.reshape(-1))

b = np.arange(3).reshape(-1, 1)

print(b.reshape(-1))

# [ 0 1 2 3 4 5 6 7 8 9 10 11]

# [0 1 2]

これは列ベクトルを行ベクトル化するときのほか、pyplotで複数のAxesインスタンスを行×列の形で受け取った時に、全てのインスタンスに同じ設定を適用したいときなどに1次元化してループで回す、といったようなことにも使える。

ndarray – 配列の次元・形状・サイズ

2020-04-05 / tau / コメントする

`ndim`属性～配列の次元

ndim属性は配列の次元を整数で返す。

1次元配列を1つだけ要素に持つ配列や列ベクトルの次元が2となっている点に注意。とにかく[]のネストの数だと考えればよい。

import numpy as np

a = np.array([1, 2, 3])
print(a.ndim)  # 1

b = np.array([
    [1, 2, 3],
    [4, 5, 6]
])
print(b.ndim)  # 2

c = np.array([
    [[1, 2], [3, 4]],
    [[5, 6], [7, 8]]
])
print(c.ndim)  # 3

d = np.array([[1, 2, 3]])
print(d.ndim)  # 2

e = np.array([
    [1],
    [2],
    [3],
])
print(e.ndim)  # 2

import numpy as np

a = np.array([1, 2, 3])

print(a.ndim) # 1

b = np.array([

[1, 2, 3],

[4, 5, 6]

])

print(b.ndim) # 2

c = np.array([

[[1, 2], [3, 4]],

[[5, 6], [7, 8]]

])

print(c.ndim) # 3

d = np.array([[1, 2, 3]])

print(d.ndim) # 2

e = np.array([

[1],

[2],

[3],

])

print(e.ndim) # 2

`shape`属性～配列の形状

shape属性は配列の形状を返す。

1次元1行の単純な配列のときにはshapeが(1, n)とならないのが気になるがこれは結果が常にタプルで返されるためで、1次元とわかっているときには1つの整数が返ってくると考えてよい。

ndim=2となる形状の場合にはタプルも2要素となって、shape=(行数, 列数)となる。より多次元の場合、外側の次元の要素数からの順番になる。

import numpy as np

a = np.array([1, 2, 3])
print(a.shape)  # (3,)

b = np.array([
    [1, 2, 3],
    [4, 5, 6]
])
print(b.shape)  # (2, 3)

c = np.array([
    [[11, 12, 13, 14],
     [15, 16, 17, 18],
     [19, 20, 21, 22]],
    [[51, 52, 53, 54],
     [55, 56, 57, 58],
     [59, 60, 61, 62]]
])
print(c.shape)  # (2, 3, 4)

d = np.array([[1, 2, 3]])
print(d.shape)  # (1, 3)

e = np.array([
    [1],
    [2],
    [3],
])
print(e.shape)  # (3, 1)

import numpy as np

a = np.array([1, 2, 3])

print(a.shape) # (3,)

b = np.array([

[1, 2, 3],

[4, 5, 6]

])

print(b.shape) # (2, 3)

c = np.array([

[[11, 12, 13, 14],

[15, 16, 17, 18],

[19, 20, 21, 22]],

[[51, 52, 53, 54],

[55, 56, 57, 58],

[59, 60, 61, 62]]

])

print(c.shape) # (2, 3, 4)

d = np.array([[1, 2, 3]])

print(d.shape) # (1, 3)

e = np.array([

[1],

[2],

[3],

])

print(e.shape) # (3, 1)

`size`属性～配列のサイズ

size属性で得られる配列のサイズは配列の要素数。

import numpy as np

a = np.array([1, 2, 3])
print(a.size)  # 3

b = np.array([
    [1, 2, 3],
    [4, 5, 6]
])
print(b.size)  # 6

c = np.array([
    [[1, 2], [3, 4]],
    [[5, 6], [7, 8]]
])
print(c.size)  # 8

d = np.array([[1, 2, 3]])
print(d.size)  # 3

e = np.array([
    [1],
    [2],
    [3],
])
print(e.size)  # 3

import numpy as np

a = np.array([1, 2, 3])

print(a.size) # 3

b = np.array([

[1, 2, 3],

[4, 5, 6]

])

print(b.size) # 6

c = np.array([

[[1, 2], [3, 4]],

[[5, 6], [7, 8]]

])

print(c.size) # 8

d = np.array([[1, 2, 3]])

print(d.size) # 3

e = np.array([

[1],

[2],

[3],

])

print(e.size) # 3

Python – file

2020-03-30 / tau / コメントする

osパッケージのgetcwd()を使ってカレントディレクトリーを取得しようとして、Atomからの直接実行などのときにうまくいかなかった。

このような場合、__file__で実行ファイルの位置を得ることができる。また、os.path.dirname(__file__)でファイル名を除いたパスを、os.path.basename(__file__)でファイル名のみを得ることができる。

実行方法によってはエラーとなる。

import os

print("__file__:{}".format(__file__))
print("dirname :{}".format(os.path.dirname(__file__)))
print("basename:{}".format(os.path.basename(__file__)))
print("files   :{}".format(os.listdir(os.path.dirname(__file__))))

import os

print("__file__:{}".format(__file__))

print("dirname :{}".format(os.path.dirname(__file__)))

print("basename:{}".format(os.path.basename(__file__)))

print("files :{}".format(os.listdir(os.path.dirname(__file__))))

Atomから実行した場合

__file__:C:\Users\...\dev\python\packages\os\__file__.py
dirname :C:\Users\...\dev\python\packages\os
basename:__file__.py
files   :[..., '__file__.py']

__file__:C:\Users\...\dev\python\packages\os\__file__.py

dirname :C:\Users\...\dev\python\packages\os

basename:__file__.py

files :[..., '__file__.py']

コマンドラインから実行ファイル(__file__.py)のあるディレクトリーに移動し、直接ファイル名をタイプした場合

C:\Users\...\dev\python\packages\os>__file__.py
__file__:C:\Users\...\dev\python\packages\os\__file__.py
dirname :C:\Users\...\dev\python\packages\os
basename:__file__.py
files   :[..., '__file__.py']

C:\Users\...\dev\python\packages\os>__file__.py

__file__:C:\Users\...\dev\python\packages\os\__file__.py

dirname :C:\Users\...\dev\python\packages\os

basename:__file__.py

files :[..., '__file__.py']

コマンドラインから実行ファイル(__file__.py)のあるディレクトリーに移動し、”python 実行ファイル名”で実行した場合

C:\Users\tomo\...\dev\python\packages\os>python __file__.py
__file__:__file__.py
dirname :
basename:__file__.py
Traceback (most recent call last):
  File "__file__.py", line 6, in <module>
    print("files   :{}".format(os.listdir(os.path.dirname(__file__))))
FileNotFoundError: [WinError 3] 指定されたパスが見つかりません。: ''

C:\Users\tomo\...\dev\python\packages\os>python __file__.py

__file__:__file__.py

dirname :

basename:__file__.py

Traceback (most recent call last):

File "__file__.py", line 6, in <module>

print("files :{}".format(os.listdir(os.path.dirname(__file__))))

FileNotFoundError: [WinError 3] 指定されたパスが見つかりません。: ''

上記と同じだが、実行ファイル名を相対パスで指定した場合

C:\Users\...\dev\python\packages\os>python ./__file__.py
__file__:C:\Users\...\dev\python\packages\os\__file__.py
dirname :C:\Users\...\dev\python\packages\os
basename:__file__.py
files   :[..., '__file__.py']

C:\Users\...\dev\python\packages\os>python ./__file__.py

__file__:C:\Users\...\dev\python\packages\os\__file__.py

dirname :C:\Users\...\dev\python\packages\os

basename:__file__.py

files :[..., '__file__.py']

概要

利用例

利用方法

モデルクラスのインポート

モデルのインスタンスの生成

モデルの学習

適合度の計算

その他のメソッド

概要

決定境界

3次元表示

概要

利用例

配列による場合

DataFrameによる場合

利用方法

モデルクラスのインポート

モデルのインスタンスの生成

モデルの学習

適合度の計算

モデルによる予測

切片・係数の利用

実行例

例示用の配列

単一の行・列の抽出

単一の行の抽出

単一の列の抽出

連続する複数の行・列の抽出

連続する複数行の抽出

連続する複数列の抽出

不連続な複数の行・列を抽出

不連続な複数の行を抽出

不連続な複数の列の抽出

概要

各種図形

概要

学習率曲線

基本

暗黙指定

1次元化するときの注意

ndim属性～配列の次元

shape属性～配列の形状

size属性～配列のサイズ

`ndim`属性～配列の次元

`shape`属性～配列の形状

`size`属性～配列のサイズ