ハノイの塔とは
ハノイの塔とは、以下のような問題。
- 3本の棒があり、そのうちの1本に直径が異なる複数の板が直径順に重ねられている
- 1回の移動で1枚の板を移動するが、移動する板はそれより板がない棒か自身より直径が大きな板がある棒にしか移動できない
- 全ての板が直径順に、異なる棒に移動し終えたら終了
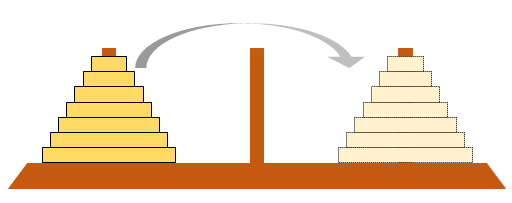
問題例
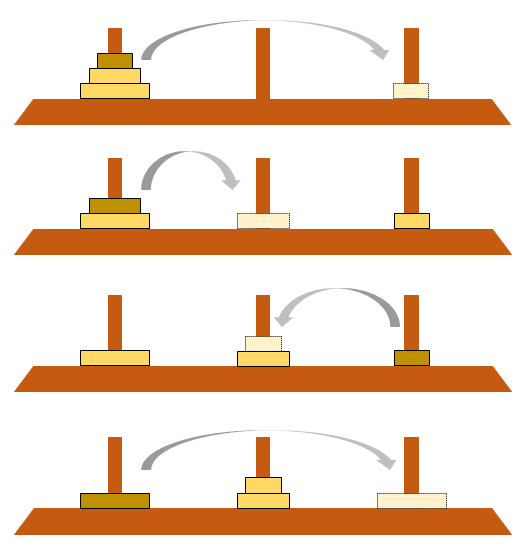
たとえば板が3枚の場合は以下のような手順になる。
まず一番下の板を動かすため、
- 最小の板を他の棒に移動(0→2)
- 次に2番目の板を別の棒に移動(0→1)
- 最小の板を2番目の板の上に移動(2→1)
- 最大の板を空いている棒に移動(0→2)
なお、3つの棒を左から0、1、2としている。
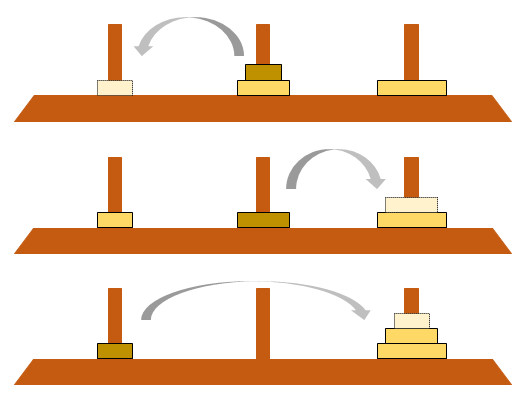
次に2番目に大きい板を動かすため
- 最小の板を空いている棒に移動(1→0)
- 2番目の板を最大の板の上に移動(1→2)
最後に1番目の板を2番目の板の上に移動して終了(0→2)
再帰手続き化
これの手続を、次のように一般化する。
まず、n枚の山を3つの軸(org、tmp、dst)のorgからdstに移動する関数を考える。
move(n, org, tmp, dst)
n動かす山の板の枚数org動かす山がある軸tmp作業用に使う軸dst山を動かす先の軸
この関数は、n枚で受け取った山を軸orgから軸dstへ移動するため、この手続きを次のように再帰的に呼び出す。
Step-1:orgからn-1枚の山をtmpに移動。
move(n-1, org, dst, tmp)
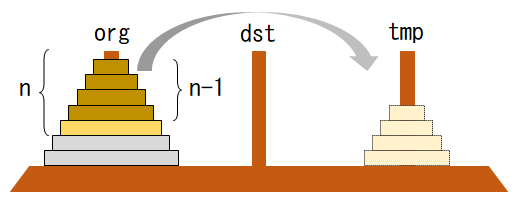
Step-2:orgに残った1枚の板をorgに移動
move(1, org, tmp, dst)
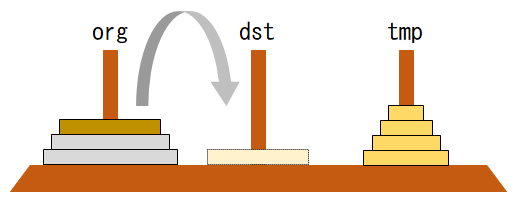
Step-3:tmpに移したn-1枚の山をdstに移動
move(n-1, tmp, org, dst)
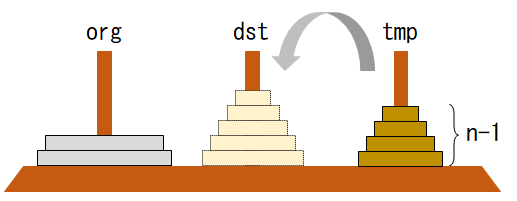
ただし山の板の枚数が1の場合はそれ以上再帰呼び出しはせず、板があった軸orgと動かした先の軸dstを記録して復帰。
プログラム化
移動過程を軸番号で表示するだけの処理
コード
移動過程を記録するだけならシンプルで、再帰関数を以下のように定義。一枚の板の移動の場合に移動軸を記録・蓄積し、その結果をコンソールに表示している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
def move(n, org, tmp, dst, solution): if n == 1: solution.append((org, dst)) return else: move(n-1, org, dst, tmp, solution) move(1, org, tmp, dst, solution) move(n-1, tmp, org, dst, solution) org, tmp, dst = 0, 1, 2 n = 3 solution = [] move(n, org, tmp, dst, solution) for movement in solution: print(movement) |
実行結果
板が3枚の場合の結果。左側の軸にある一番上の板を、右側の軸に移動することを意味している。
|
1 2 3 4 5 6 7 |
(0, 2) (0, 1) (2, 1) (0, 2) (1, 0) (1, 2) (0, 2) |
クラス化・画面表示
ハノイの塔を解いていく過程を表示させる。単純なコンソール表示であっても、盤の状態保持やその表示など、コアのアルゴリズムとは別の部分でコードが増える。クラスを作っていくと更にコードが増えるが、全体の見通しはよくなる。
HanoiShaftクラス
盤上の軸のクラス。板を置いたり取り除くほか、任意の位置(高さ)にある板が何か知ることができる。板は直径の小さい順に1, 2, 3,…と整数で表し、軸上の指定位置に板がない場合は0。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class HanoiShaft: def __init__(self): self.shaft = [] def disk_at(self, layer): return 0 if len(self.shaft) < layer + 1 else self.shaft[layer] def put(self, disk): self.shaft.append(disk) def remove(self): return self.shaft.pop() |
Hanoiクラス
盤の状態を保持し、問題を解き、その結果を表示するクラス。問題を解く部分と、実態の盤の状態保持や表示は別のものだが、それらをまとめている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
class Hanoi: def __init__(self, num_disks): self.num_disks = num_disks self.solution = [] self.shafts = [HanoiShaft() for n in range(3)] org, tmp, dst = 0, 1, 2 for disk in range(num_disks, 0, -1): self.shafts[org].put(disk) def solve(self): self.solution = [] self.move(self.num_disks, 0, 1, 2) def move(self, n, org, tmp, dst): if n == 1: self.solution.append((org, dst)) return else: self.move(n-1, org, dst, tmp) self.move(1, org, tmp, dst) self.move(n-1, tmp, org, dst) def display_solution(self): self.display_status() self.solve() for movement in self.solution: disk = self.shafts[movement[0]].remove() self.shafts[movement[1]].put(disk) self.display_status() def display_status(self): max_width = self.num_disks * 2 - 1 for layer in range(self.num_disks-1, -1, -1): layer_str = '' for shaft in self.shafts: disk = shaft.disk_at(layer) if disk == 0: space_size = (max_width - 1) // 2 layer_str += ' '*space_size + '|' + ' '*space_size + ' ' else: disk_size = disk * 2 - 1 space_size = (max_width - disk_size) // 2 layer_str += \ ' '*space_size + '#'*disk_size + ' '*space_size + ' ' print(layer_str) print('-'*(max_width*3+2)) print() |
実行部分
|
1 2 |
hanoi = Hanoi(3) hanoi.display_solution() |
実行結果
板が3枚の場合の結果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
# | | ### | | ##### | | ----------------- | | | ### | | ##### | # ----------------- | | | | | | ##### ### # ----------------- | | | | # | ##### ### | ----------------- | | | | # | | ### ##### ----------------- | | | | | | # ### ##### ----------------- | | | | | ### # | ##### ----------------- | | # | | ### | | ##### ----------------- |
手続回数
もう一度、以下の再帰手続きを考える。
|
1 2 3 4 5 6 7 8 |
def move(n, org, tmp, dst, solution): if n == 1: solution.append((org, dst)) return else: move(n-1, org, dst, tmp, solution) move(1, org, tmp, dst, solution) move(n-1, tmp, org, dst, solution) |
n個の山の計算でn-1個の山の関数を2つ呼び出し、それらがまたn-2個の山の関数を2つずつ呼び出す。
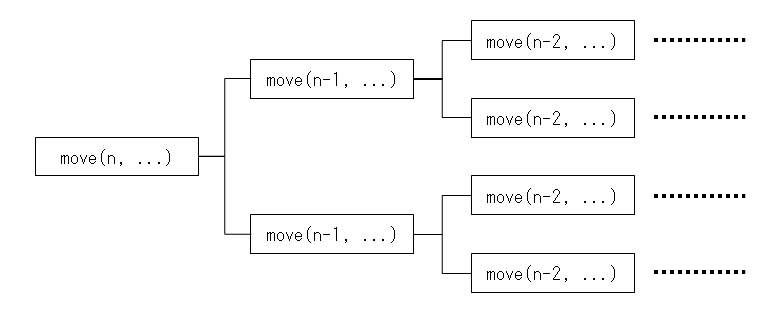
計算回数はこれらの和なので、n個の山における関数の呼び出し回数![]() は以下の通り。
は以下の通り。
![]()
したがって、階乗計算のように一次的な再帰と異なり、nが1増えるごとに計算量が2倍に増えていくことに注意が必要。