概要
waveデータセットは、”Pythonではじめる機械学習”(O’REILLY)中で用いられる架空のデータセットである。
その内容は、引数n_samplesで指定した個数の点について1つの特徴量とターゲットの値を持ち、回帰を扱うのに適している。
利用方法
mglearnパッケージから、たとえば以下のように利用する。
|
1 2 3 |
from mglearn.datasets import make_wave X, y = make_wave(n_samples=40) |
実行するとdeprecatedの警告が出るが、放置してもよいらしい。
内容
waveデータの特徴は以下の通り。
- 引数の
n_samplesには任意の整数を指定できる - 特徴量(x座標の値)は決まっている
n_samplesが増えてもx0, x1, …の値は変わらない- x0, x1, …は実行のたびに同じパターン
- ターゲットの値(y座標の値)は変化するが実行ごとに同じ
n_samplesが変わると同じx0, x1, …の値に対するy0, y1, …の値は変化する- y0, y1, …は実行のたびに同じパターン
このことを、n_samplesの値を変化させたときのX, yの内容で確認してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
import matplotlib.pyplot as plt from mglearn.datasets import make_wave n_samples_list = [1, 2, 3, 4, 5, 6] for n_samples in n_samples_list: X, y = make_wave(n_samples=n_samples) print("\nn_samples={}".format(n_samples)) for u, v in zip(X, y): print("({:6.3f}, {:6.3f})".format(u[0], v)) # n_samples=1 # (-0.7528, -0.9974) # # n_samples=2 # (-0.7528, -0.1176) # ( 2.7043, 1.6216) # # n_samples=3 # (-0.7528, -0.9974) # ( 2.7043, 1.0195) # ( 1.3920, 0.5076) # # n_samples=4 # (-0.7528, -0.5585) # ( 2.7043, 0.7430) # ( 1.3920, 1.1577) # ( 0.5920, 1.0291) # # n_samples=5 # (-0.7528, -0.3020) # ( 2.7043, 1.3653) # ( 1.3920, 0.0776) # ( 0.5920, 0.3828) # (-2.0639, -1.7779) # # n_samples=6 # (-0.7528, 0.3481) # ( 2.7043, 1.2438) # ( 1.3920, 0.1333) # ( 0.5920, 0.9167) # (-2.0639, -1.7239) # (-2.0640, -1.7250) |
このコードは何度実行しても同じ値を返す。x座標のパターンが変わっていないこと、y座標のパターンは実行のたびに変化していることがわかる。ただし異なるn_sampleに対して、同じxに対するyの値は大きくは変化していない。
なお、n_samplesが6の時のxの最後の値とその1つ前の値がかなり近く、対応するyの値も近い。n_samplesが1の時と3の時に、先頭のXとyの値が殆ど等しい。
以上のことから、waveデータセットはXについては毎回同じ系列でランダムな値を返し、yはXに対して一定の計算値に毎回同じ系列の乱数で擾乱を加えていると想像される。
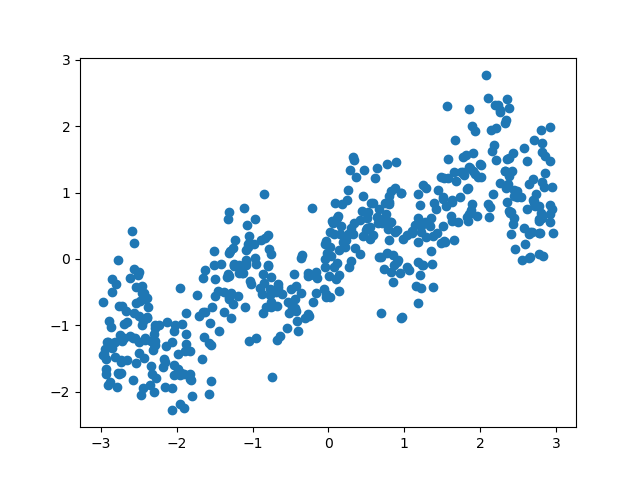
最後に、n_samplesを多くしたときの結果を見てみると明らかに線形で上昇しつつ波打っているのがわかる。おそらく![]() のような式に擾乱を与えていると思われる。
のような式に擾乱を与えていると思われる。
手法の適用