概要
k-最近傍回帰の例として、scikit-learnのwaveデータにKNeighborsRegressorを適用してみた結果。
近傍点数とクラス分類の挙動
訓練データとして10個のwaveデータを訓練データとして与え、2つのテストデータの予測するのに、近傍点数を1, 2, 3と変えた場合の様子を見てみる。
近傍点数=1の場合
2つのテストデータの特徴量の値に最も近い特徴量を持つ訓練データが選ばれ、その属性値がそのままテストデータの属性値となっている。
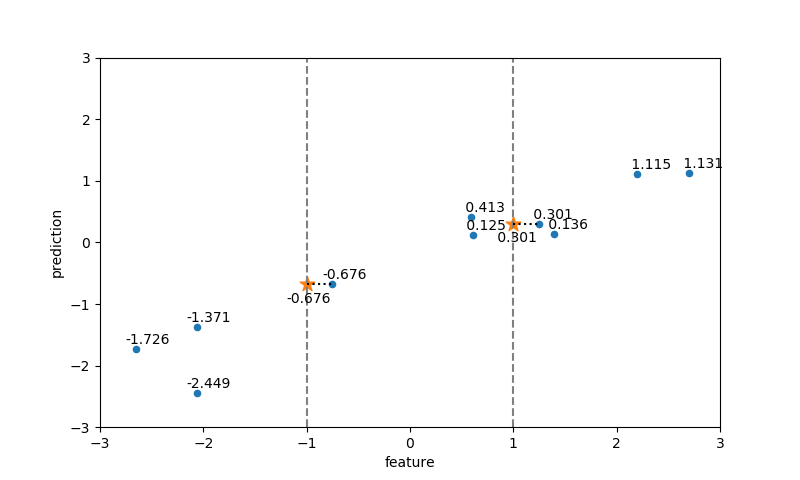
近傍点数=2の場合
テストデータの特徴量に最も近い方から1番目、2番目の特徴量を持つ訓練データが選ばれ、それらの属性値の平均がテストデータの属性値となっている。
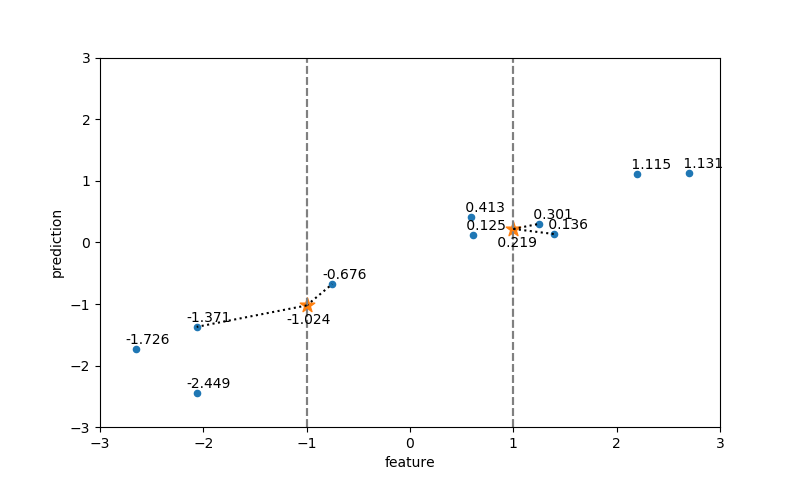
近傍点数=3の場合
同様に、テストデータの特徴量に最も近い3つの訓練データの属性の平均がテストデータの属性値となっている。
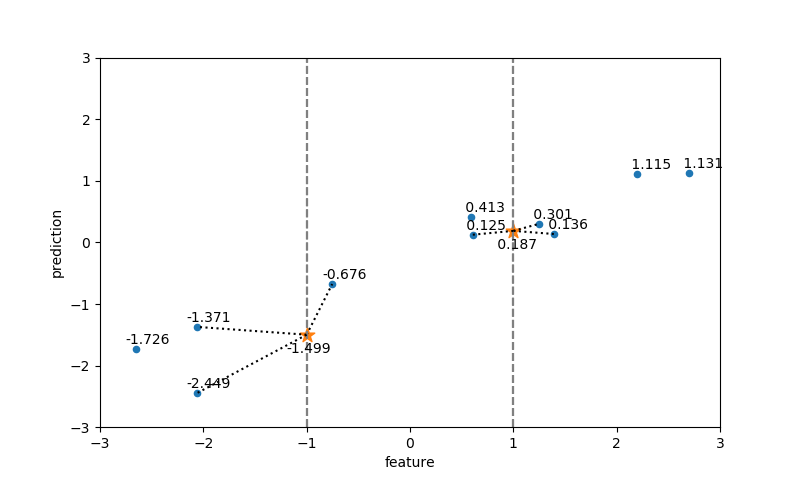
実行コード
上記の計算のコードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
import numpy as np import matplotlib.pyplot as plt from sklearn.neighbors import KNeighborsRegressor from mglearn.datasets import make_wave X_train, y_train = make_wave(n_samples=10) reg = KNeighborsRegressor(n_neighbors=3) reg.fit(X_train, y_train) X_test = np.array([[-1], [1]]) y_pred = reg.predict(X_test) neigh_dist, neigh_ind = reg.kneighbors(X=X_test) print(neigh_ind) fig, ax = plt.subplots(figsize=(8.0, 4.8)) xmin, xmax = -3, 3 ymin, ymax = -3, 3 ax.scatter(X_train, y_train, marker='o', s=20) ax.scatter(X_test, y_pred, marker='*', s=120) for test, pred, ind in zip(X_test, y_pred, neigh_ind): for neigh in ind: ax.plot([test, test], [ymin, ymax], c='gray', linestyle='dashed') ax.plot( [test[0], X_train[neigh, 0]], [pred, y_train[neigh]], color='k', linestyle='dotted') for x, y in zip(X_train, y_train): ax.annotate("{:6.3f}".format(y), xy=(x[0] - 0.1, y + 0.08)) for x, y in zip(X_test, y_pred): ax.annotate("{:6.3f}".format(y), xy=(x[0] - 0.2, y - 0.3)) ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.set_xlabel("feature") ax.set_ylabel("prediction") plt.show() |
knnの精度
O’Reillyの”Pythonではじめる機械学習”中、KNeighborsRegressorのwaveデータに対する精度が計算されている。40サンプルのwaveデータを発生させ訓練データとテストデータに分け、テストデータに対するR2スコアが0.83となることが示されている。実際に計算してみると、確かに同じ値となる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np from sklearn.neighbors import KNeighborsRegressor from sklearn.model_selection import train_test_split from mglearn.datasets import make_wave X_source, y_source = make_wave(n_samples=40) X_train, X_test, y_train, y_test =\ train_test_split(X_source, y_source, random_state=0) reg = KNeighborsRegressor(n_neighbors=3) reg.fit(X_train, y_train) y_pred = reg.predict(X_test) print("R^2 score:{:6.3f}".format(reg.score(X_test, y_test))) # R^2 score: 0.834 |
これを見ると比較的高い精度のように見えるが、train_test_split()の引数random_stateを変化させてみると以下のように精度はばらつく。乱数系列が異なると精度が0.3未満の場合もあるが、全体としてみると0.6~0.7あたりとなりそうである。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
import numpy as np from sklearn.neighbors import KNeighborsRegressor from sklearn.model_selection import train_test_split from mglearn.datasets import make_wave X_source, y_source = make_wave(n_samples=40) reg = KNeighborsRegressor(n_neighbors=3) print("random_state -> R^2") for random_state in range(0, 10): X_train, X_test, y_train, y_test =\ train_test_split(X_source, y_source, random_state=random_state) reg.fit(X_train, y_train) y_pred = reg.predict(X_test) print("{} -> {:6.3f}".format(random_state, reg.score(X_test, y_test))) # random_state -> R^2 # 0 -> 0.834 # 1 -> 0.581 # 2 -> 0.798 # 3 -> 0.281 # 4 -> 0.773 # 5 -> 0.738 # 6 -> 0.554 # 7 -> 0.494 # 8 -> 0.678 # 9 -> 0.801 |
ためしにmake_wave(n_samples=1000)としてみると、結果は以下の通りとなり、精度は0.67程度(平均は0.677)と一定してくる。
|
1 2 3 4 5 6 7 8 9 10 11 |
random_state -> R^2 0 -> 0.679 1 -> 0.662 2 -> 0.682 3 -> 0.672 4 -> 0.680 5 -> 0.697 6 -> 0.712 7 -> 0.682 8 -> 0.661 9 -> 0.641 |
予測カーブ
訓練データが少ない場合
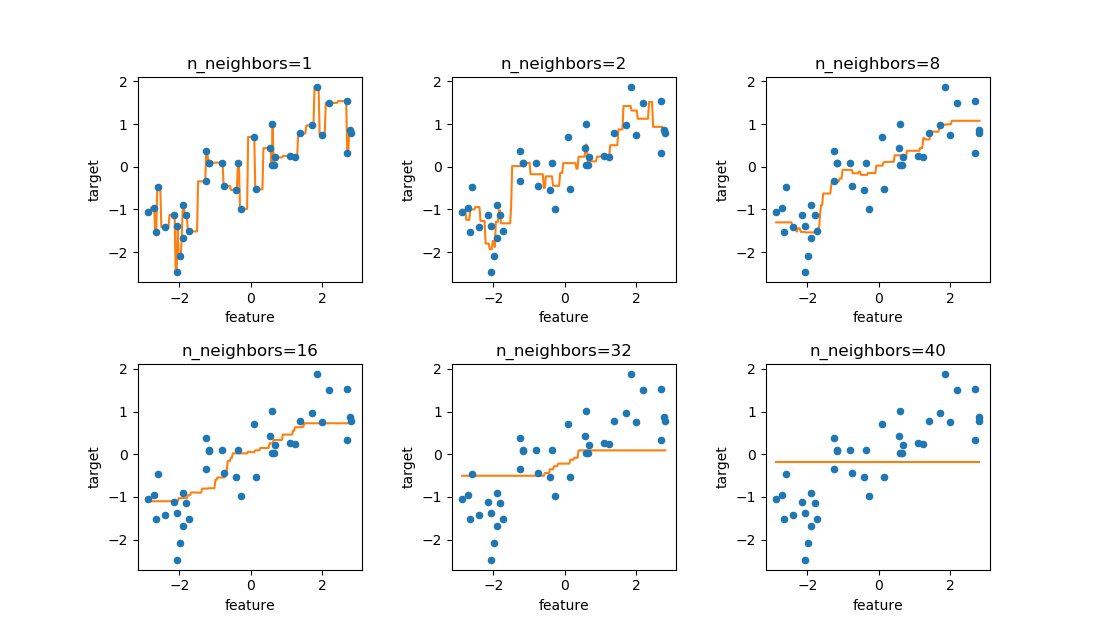
40個のwaveデータに対して、n_neighborsを変化させたときの予測カーブを見てみる。
n_neighbors=1の時は、全ての訓練データを通るような線となるn_neighborsが多くなるほど滑らかになるn_neighborsがかなり大きくなると水平に近くなるn_neighborsが訓練データ数と同じになると、予測線は水平になる(任意の特徴量に対して、全ての点の平均を計算しているため)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import numpy as np import matplotlib.pyplot as plt from sklearn.neighbors import KNeighborsRegressor from mglearn.datasets import make_wave X_train, y_train = make_wave(n_samples=40) xmin = np.min(X_train[:, 0]) xmax = np.max(X_train[:, 0]) X_test = np.linspace(xmin, xmax, 200).reshape(-1, 1) fig, axs = plt.subplots(2, 3, figsize=(11, 6.4)) plt.subplots_adjust(hspace=0.4, wspace=0.4) n_neighbors_list=[1, 2, 8, 16, 32, 40] axs_1d = axs.reshape(1, -1)[0] for ax, n_neighbors in zip(axs_1d, n_neighbors_list): reg = KNeighborsRegressor(n_neighbors=n_neighbors) reg.fit(X_train, y_train) y_pred = reg.predict(X_test) ax.scatter(X_train[:, 0], y_train, zorder=2, s=20, color='tab:blue') ax.plot(X_test, y_pred, zorder=1, color='tab:orange') ax.set_title("n_neighbors={}".format(n_neighbors)) ax.set_xlabel("feature") ax.set_ylabel("target") plt.show() |
訓練データが多い場合
今度はwaveデータでn_samples=200と数を多くしてみる。データ数を多くするとその名の通り、上下に波打ちながら増加している様子が見られる。これに対してn_neighborsを変化させたのが以下の図。
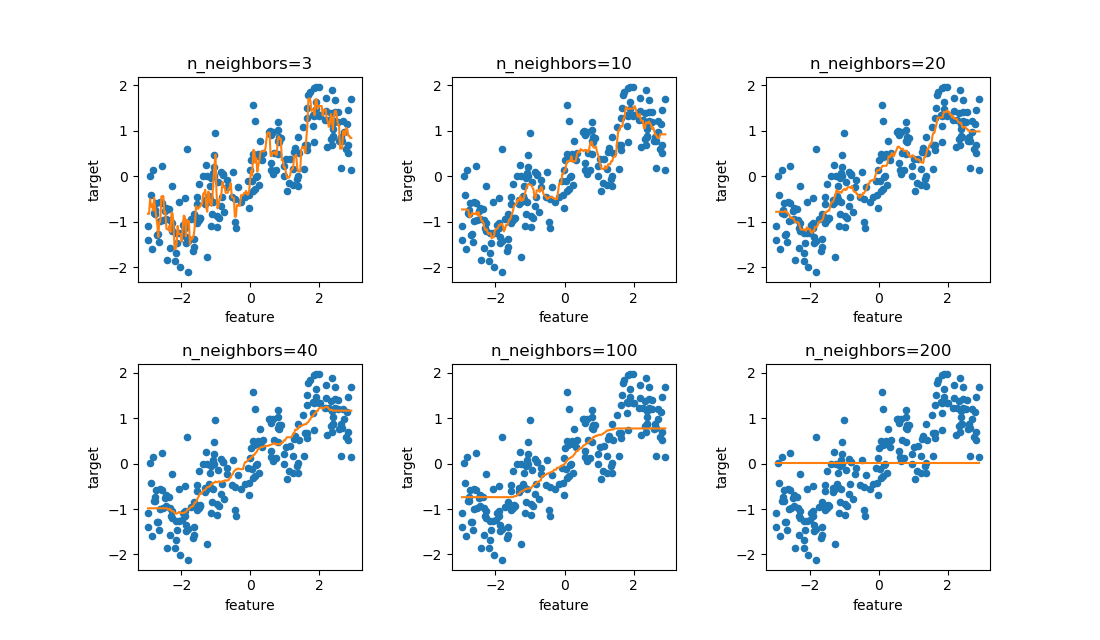
n_neighbors=10~20あたりで滑らかに、かつ波打つ状況が曲線で再現されている。
n_samples=300として訓練データに200を振り分け、n_neighborsを変化させたときのスコアは以下の通り。n_neighbors=20あたりで精度が最もよさそうである。
あるデータが得られたとき、その科学的なメカニズムは置いておいて、とりあえずデータから予測値を再現したいときにはそれなりに使えるかもしれない。
|
1 2 3 4 5 6 7 8 9 |
n_neighbors -> R^2 5 -> 0.754 10 -> 0.788 15 -> 0.789 20 -> 0.792 25 -> 0.777 50 -> 0.737 100 -> 0.613 200 -> -0.022 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np from sklearn.neighbors import KNeighborsRegressor from sklearn.model_selection import train_test_split from mglearn.datasets import make_wave X_source, y_source = make_wave(n_samples=300) X_train, X_test, y_train, y_test =\ train_test_split(X_source, y_source, train_size=200, random_state=0) n_neighbors_list = [5, 10, 15, 20, 25, 50, 100, 200] print("n_neighbors -> R^2") for n_neighbors in n_neighbors_list: reg = KNeighborsRegressor(n_neighbors=n_neighbors) reg.fit(X_train, y_train) y_pred = reg.predict(X_test) print("{} -> {:6.3f}".format(n_neighbors, reg.score(X_test, y_test))) |