イベント制御によるポアソン過程のシミュレーション

2016-09-12 / tau / コメントする

イベント制御による分析

時刻制御(time driven)では微小な時間間隔の間において到着イベントを確率的に発生させた。そこでは結果としての到着時間間隔の指数分布や到着数のPoisson分布は前提にはおかれていない。

イベント制御(event driven)の考え方では、ある到着があった後、次の到着までの時間間隔を指数分布に従う乱数を発生させて計算する。計算にはR言語を使う。

イベント制御の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。

到着イベントの時系列

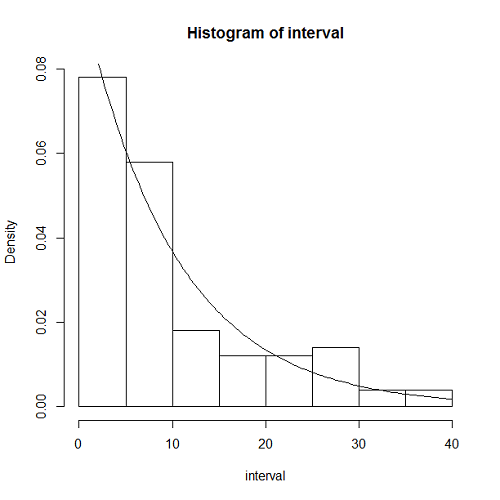
ここでは、到着率はこれまでと同じλ = 1/10として、時刻t = 0からt ≤ 1000秒の間、到着の時間間隔が確率密度 $e^{- \lambda t}$ の指数分布に従うような乱数を発生させていく。

指数分布に従う乱数を生成するには逆関数法を使う。

指数分布の確率分布関数は以下の通り。

(1) $\begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}$

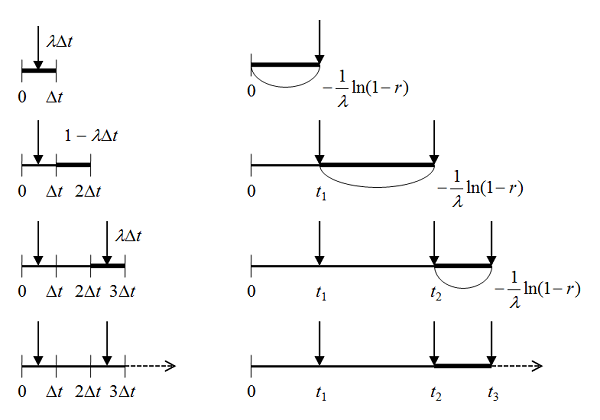
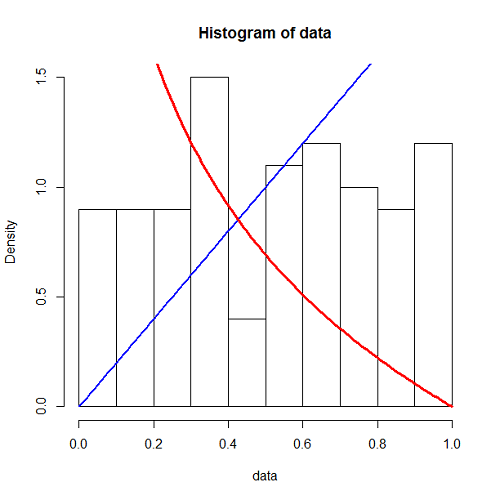
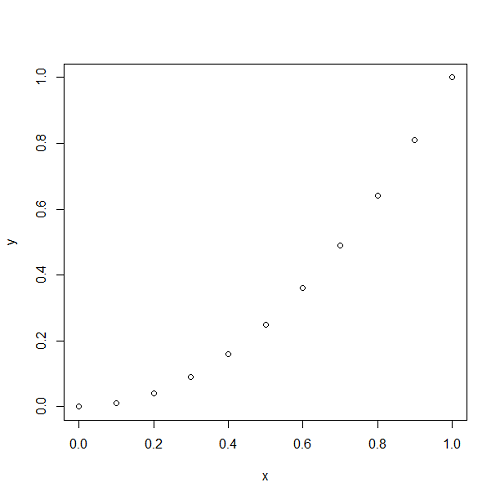
一様乱数runifを与えて指数分布に従う乱数を得るには、一様乱数を分布関数の逆関数に適用すればよい。

(2) $\begin{equation*} F^{-1}(t) = - \frac{1}{\lambda}\ ln(1 - {\rm runif(1)}) \end{equation*}$

lambda <- 1/ 10

data <- c()
for (i in 1:1000) {
  r <- (1 - log(runif(1))) / lambda
  data <- c(data, r)
}

lambda <- 1/ 10

data <- c()

for (i in 1:1000) {

r <- (1 - log(runif(1))) / lambda

data <- c(data, r)

}

時刻0を起点として、1番目の到着時刻をこの指数乱数で決定し、その次の到着時刻も指数乱数で・・・と繰り返して、時刻が上限を超えるまで時系列として記録する。

interval <- function(lambda) return( (1 - log(runif(1))) / lambda )

lambda <- 1/ 10
t.obs <- 5000
rank.width <- 100

t <- 0
arrivals <- c()
while (t < t.obs) {
  arrivals <- c(arrivals, t)
  t <- t + interval(lambda)
}

hist(arrivals, breaks=seq(0, t.obs, rank.width))

interval <- function(lambda) return( (1 - log(runif(1))) / lambda )

lambda <- 1/ 10

t.obs <- 5000

rank.width <- 100

t <- 0

arrivals <- c()

while (t < t.obs) {

arrivals <- c(arrivals, t)

t <- t + interval(lambda)

}

hist(arrivals, breaks=seq(0, t.obs, rank.width))

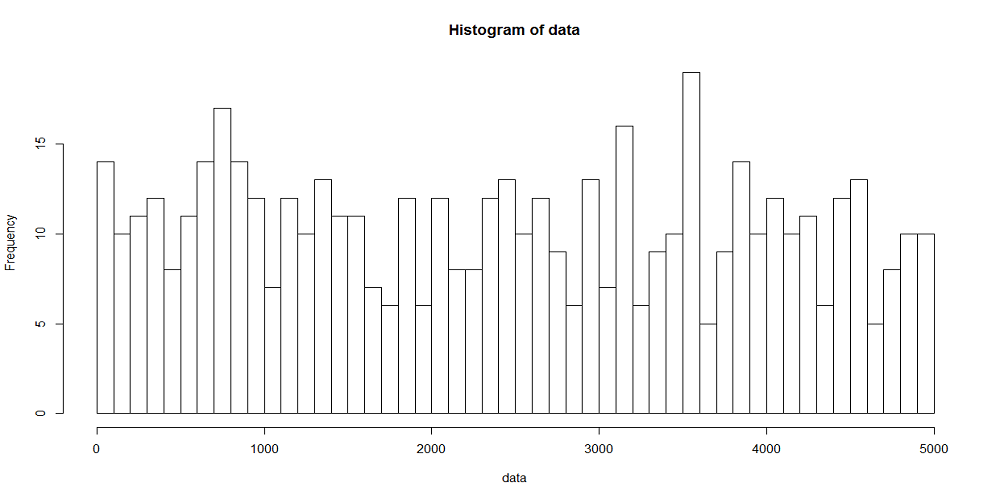
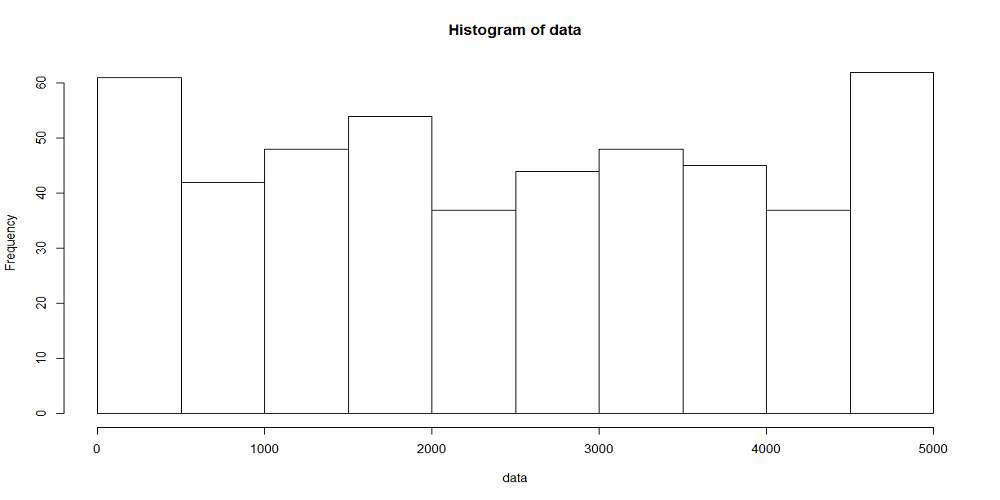
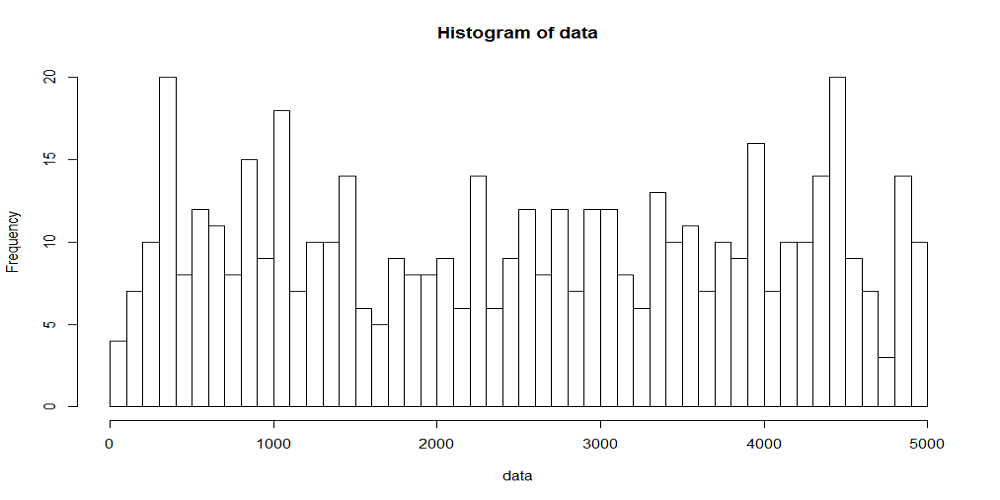
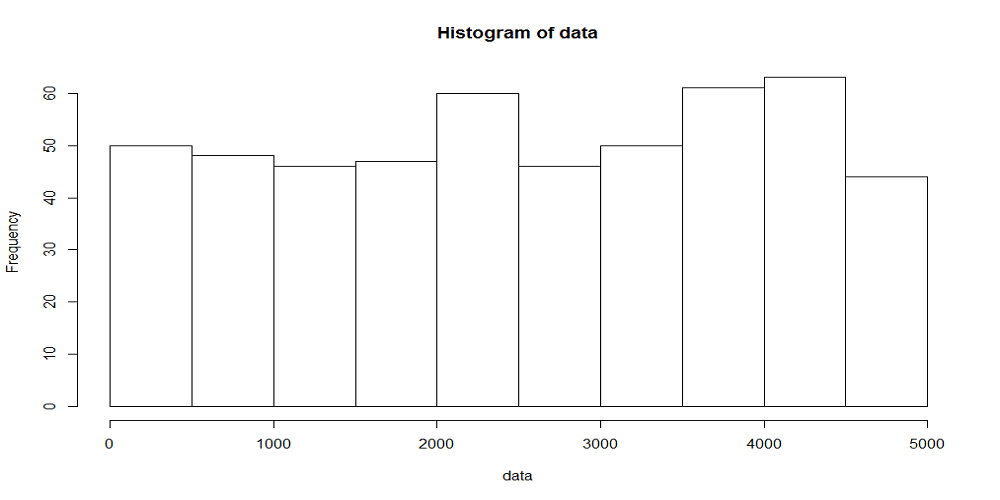
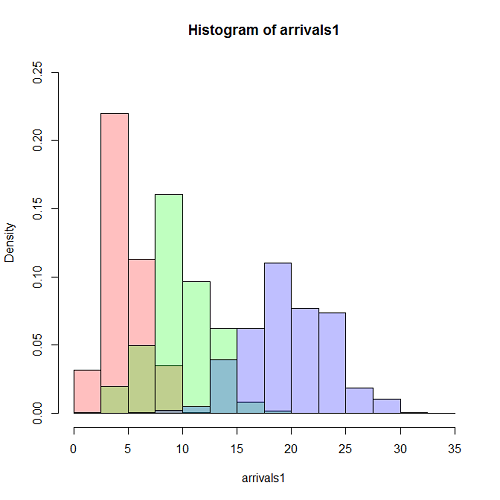
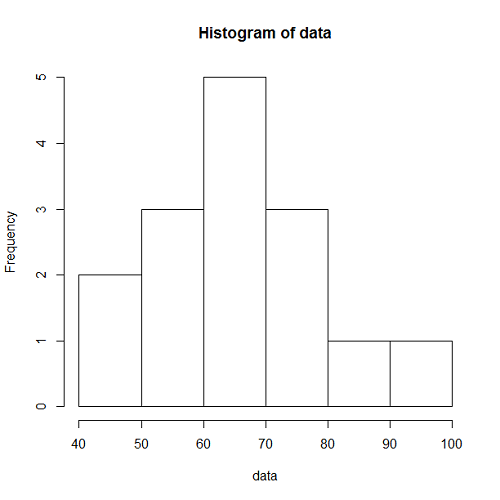
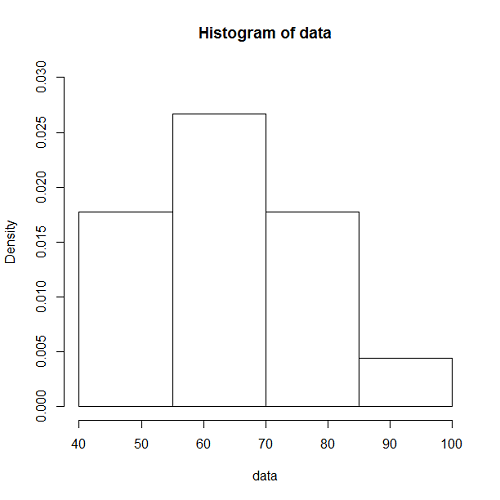
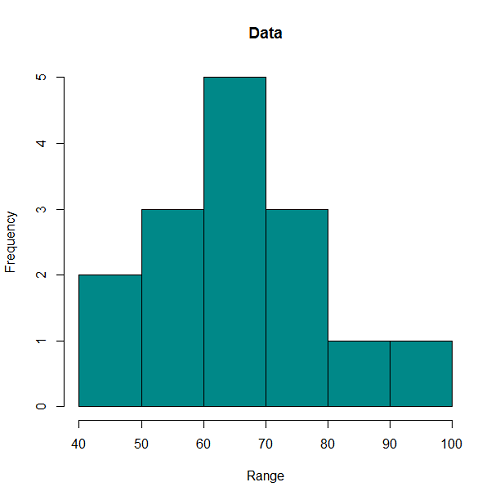
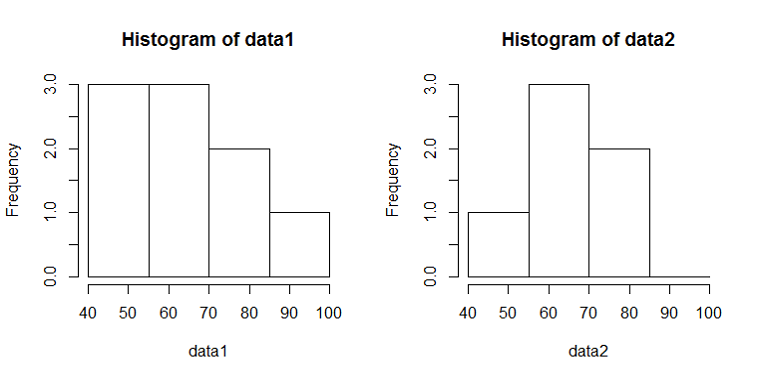
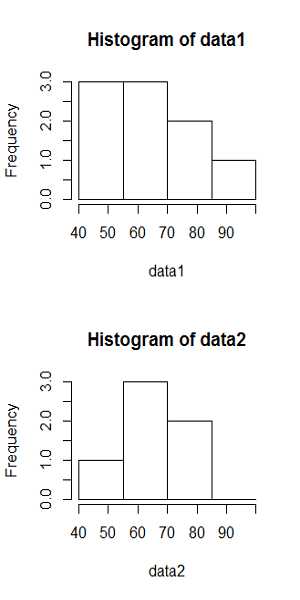
一様乱数による場合と同じく、到着率1/10、観測時間5000秒として、階級幅100秒、500秒の場合の時系列を生成したのが下図。階級あたりのデータ数と分布の平滑さの関係は、一様乱数による場合やtime drivenの場合と同じ。

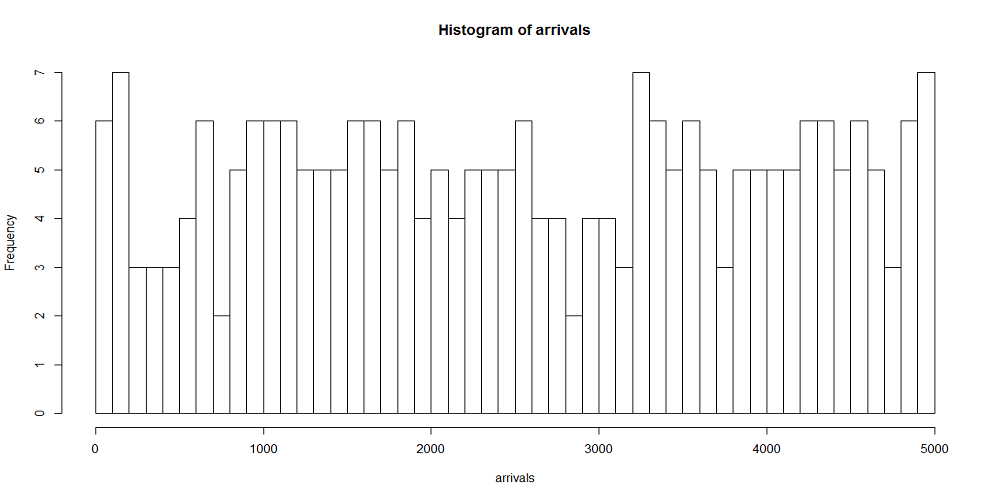
poisson-process-event-driven-arrival100

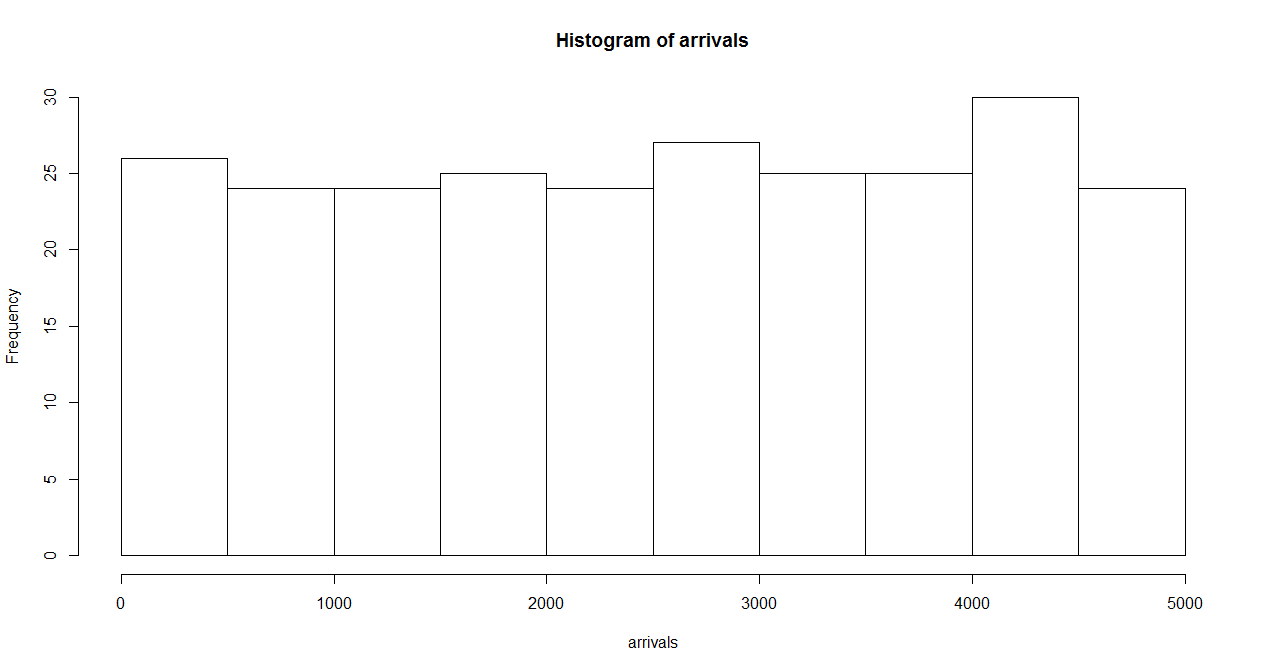
poisson-process-event-driven-arrival500

到着数の分布

到着数の確率分布は、一様乱数による場合やtime drivenと同じように集計する。

interval <- function(lambda) return( -log(1 - runif(1)) / lambda )

generate <- function(t.obs, lambda) {
  t <- 0
  data <- c()
  while (t < t.obs) {
    data <- c(data, t)
    t <- t + interval(lambda)
  }
  return (length(data))
}

lambda <- 1/ 10
t.obs <- 1000
n.loop <- 100

arrivals <- rep(0, n.loop)
for (i in 1:n.loop) arrivals[i] <- (generate(t.obs, lambda))

hist(arrivals, freq=FALSE)
curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE)

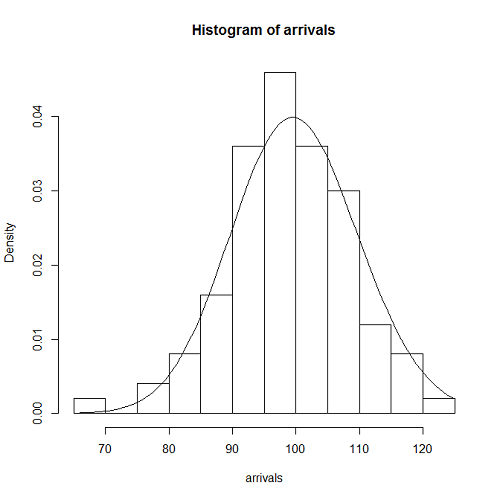
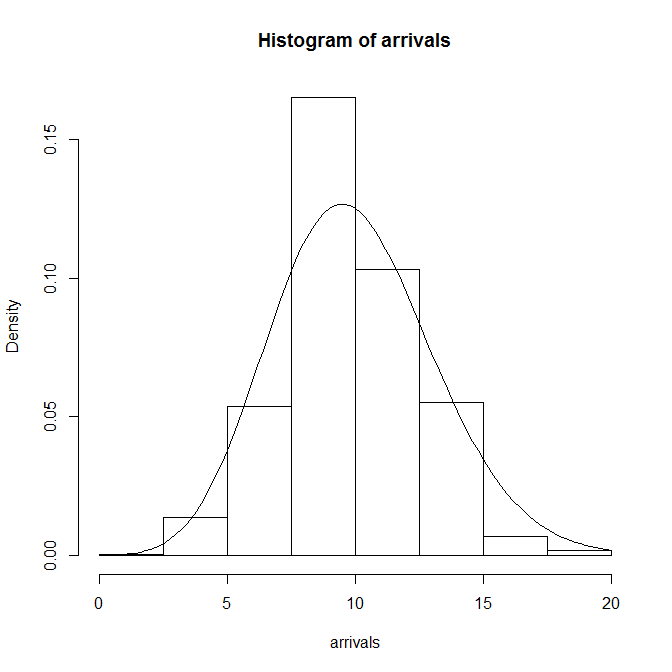
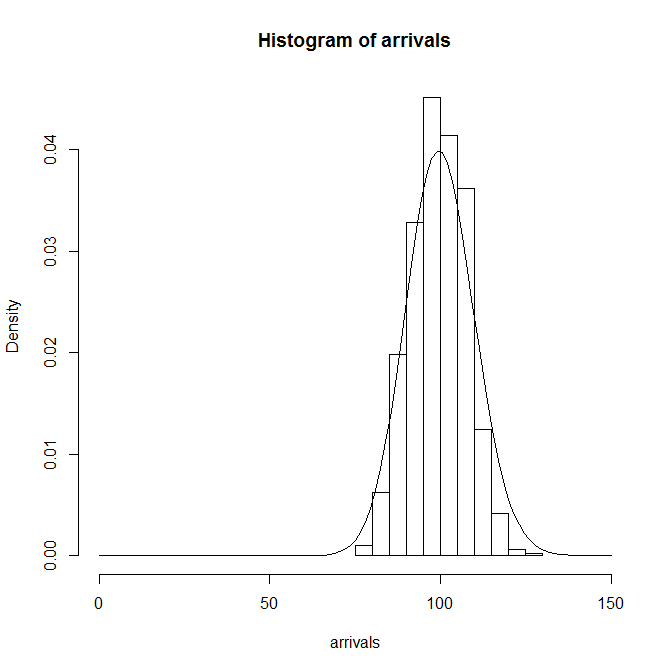
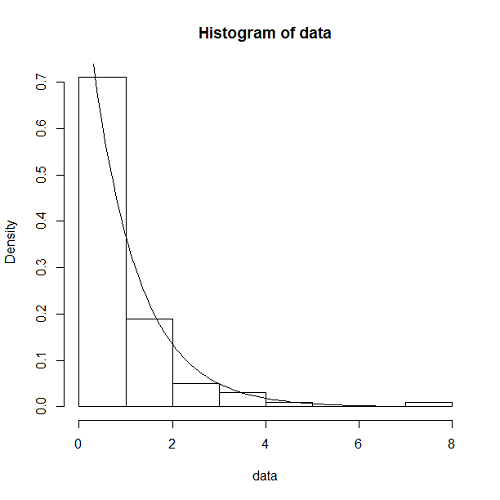
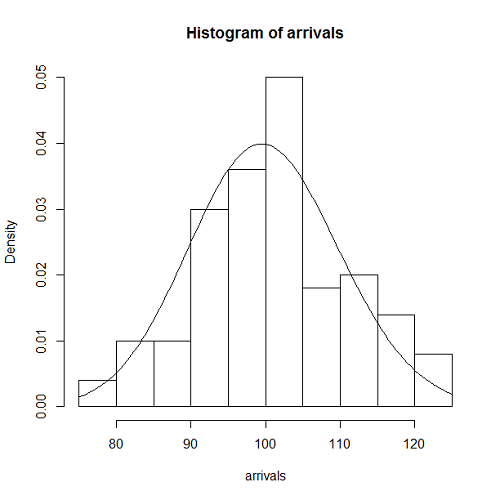
interval <- function(lambda) return( -log(1 - runif(1)) / lambda )

generate <- function(t.obs, lambda) {

t <- 0

data <- c()

while (t < t.obs) {

data <- c(data, t)

t <- t + interval(lambda)

}

return (length(data))

}

lambda <- 1/ 10

t.obs <- 1000

n.loop <- 100

arrivals <- rep(0, n.loop)

for (i in 1:n.loop) arrivals[i] <- (generate(t.obs, lambda))

hist(arrivals, freq=FALSE)

curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE)

結果は、Poisson分布の理論式ともよくあっている。

poisson-process-event-driven-poisson

時刻制御によるポアソン過程のシミュレーション

2016-09-12 / tau / コメントする

時刻制御による分析

時刻制御(time driven)の考え方では、時刻を変化させながら、その都度到着イベントが発生するかどうかを確率的に計算し、到着パターンのデータを生成していく。計算にはR言語を使う。

時刻制御の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。

到着イベントの時系列

上のRのコードでは、到着率λに短い時間間隔dtを掛けた確率でその時間間隔t ～ t + dtの間に到着イベントを発生させている。

lambda <- 1 / 10
t.obs <- 1000
dt = 0.1
nstep = floor(t.obs / dt)
rank.width <- 100

data <- c()
t <- 0
for (i in 1:nstep) {
  t <- dt * i
  if (runif(1) < lambda * dt) data <- c(data, t)
}

hist(data)

lambda <- 1 / 10

t.obs <- 1000

dt = 0.1

nstep = floor(t.obs / dt)

rank.width <- 100

data <- c()

t <- 0

for (i in 1:nstep) {

t <- dt * i

if (runif(1) < lambda * dt) data <- c(data, t)

}

hist(data)

以下に観測時間が5000秒のときの、階級幅が100秒、500秒に対する到着数の時系列分布をヒストグラムを示す。階級当たりのデータ数が多いほど平滑化される傾向は、一様分布によって到着イベントを発生させたときと同じ。

poisson-process-time-driven-arrival100

poisson-process-time-driven-arrival500

到着時間間隔の分布

一様乱数のときと同じく、到着時間間隔の分布をチェックする。期待した通り、指数分布の確率密度関数とよく合っている。

generate <- function(t.obs, lambda, dt) {
  data <- c()
  t <- 0
  for (i in 1:floor(t.obs / dt)) {
    t <- dt * i
    if (runif(1) < lambda * dt) data <- c(data, t)
  }
  return(data)
}

lambda <- 1 / 10
t.obs <- 1000
dt = 0.1

data = generate(t.obs, lambda, dt)
interval <- data[-1] - data[-length(data)]

hist(interval, freq=FALSE)
curve(dexp(x, rate=lambda), add=TRUE)

generate <- function(t.obs, lambda, dt) {

data <- c()

t <- 0

for (i in 1:floor(t.obs / dt)) {

t <- dt * i

if (runif(1) < lambda * dt) data <- c(data, t)

}

return(data)

}

lambda <- 1 / 10

t.obs <- 1000

dt = 0.1

data = generate(t.obs, lambda, dt)

interval <- data[-1] - data[-length(data)]

hist(interval, freq=FALSE)

curve(dexp(x, rate=lambda), add=TRUE)

poisson-process-time-driven-interval

到着数の分布

到着数の分布についても、一様分布のときと同じように調べると、Poisson分布の形状とよく合っている。

なおtime drivenの場合は、細かい時間間隔について到着判定をしているのでループ回数が多くなり、計算時間が少しかかる。

generate <- function(t.obs, lambda, dt) {
  data <- c()
  t <- 0
  for (i in 1:floor(t.obs / dt)) {
    t <- dt * i
    if (runif(1) < lambda * dt) data <- c(data, t)
  }
  return(data)
}

lambda <- 1 / 10
t.obs <- 1000
dt = 0.1
n.loop <- 100

arrivals <- rep(0, n.loop)
for (n in 1:n.loop) {
  data = generate(t.obs, lambda, dt)
  arrivals[n] <- length(data)
}

hist(arrivals, freq=FALSE)
curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE)

generate <- function(t.obs, lambda, dt) {

data <- c()

t <- 0

for (i in 1:floor(t.obs / dt)) {

t <- dt * i

if (runif(1) < lambda * dt) data <- c(data, t)

}

return(data)

}

lambda <- 1 / 10

t.obs <- 1000

dt = 0.1

n.loop <- 100

arrivals <- rep(0, n.loop)

for (n in 1:n.loop) {

data = generate(t.obs, lambda, dt)

arrivals[n] <- length(data)

}

hist(arrivals, freq=FALSE)

curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE)

poisson-process-time-driven-poisson

一様乱数によるポアソン過程のシミュレーション

2016-09-12 / tau / コメントする

一様乱数に基づく分析

R言語を使って、到着率をλ、観測時間をtとしてその間の到着時刻を一様乱数で発生させ、それらの分布や到着時間間隔、到着回数の分布などを確認する。

到着時刻の分布

以下の手順で到着時刻の乱数データを得てヒストグラムを描き、結果の一様性を確認する。

一様分布による到着確率の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。

観測時間tの間の平均到着数はλt
ただしtの間で個数を指定して一様乱数を発生させると、全体の到着数を縛ることになる
そこでtと同じ長さの余裕分をtの前後にとり、区間[–t, 2t)の間で3λt個の乱数を発生させる(到着時間の確率変数)
そのデータから、区間[0, t)の範囲にあるデータを抽出し、ヒストグラムを描く
その際、データの階級のレンジ～1レンジ幅の平均到着数も変化させてみる

到着率λ = 1/10[回/秒]、観測時間5000[秒]、階級レンジ100秒としたときの、Rのコードは以下の通り。このとき各階級の平均的な到着回数は1/10 * 100 = 10回程度と予想される。

lambda <- 1 / 10
t.obs <- 5000
rank.width <- 100
num.data <- lambda * t.obs

org.data <- (runif(floor(num.data * 3)) * 3 - 1) * t.obs
data <- org.data[(org.data >= 0) & (org.data < t.obs)]

ranks <- seq(0, t.obs, rank.width)
hist(data, breaks=ranks)

lambda <- 1 / 10

t.obs <- 5000

rank.width <- 100

num.data <- lambda * t.obs

org.data <- (runif(floor(num.data * 3)) * 3 - 1) * t.obs

data <- org.data[(org.data >= 0) & (org.data < t.obs)]

ranks <- seq(0, t.obs, rank.width)

hist(data, breaks=ranks)

各変数の意味は、

`lambda`	到着率λ
`t.obs`	観測時間t
`rank.width`	ヒストグラムの階級幅(時刻幅)。この幅の中の平均到着数はλ*rank_width回。
`org.data`	前後に余裕幅を持たせた元データ
`data`	t.obsの範囲内だけを切り出したデータ

まず、rank.width = 100すなわち時刻幅あたりの平均到着数が10回の場合の分布をみてみる。

poisson-process-uniform-dist-n010

各時刻幅で到着数が変動していて、平均10回の到着が想定されるところに3～20回とばらついている。

次にrank.width = 500すなわち時刻幅あたりの平均到着数が50回の場合の分布をみてみると、今度は随分と各時刻幅での到着回数が揃ってきているのが確認できる。

poisson-process-uniform-dist-n050

到着時間間隔の分布

到着時間間隔は、時系列上としてソートされた到着データてn番目の要素からn – 1番目の要素を引いて得られる。この計算は、到着データの先頭を除いたベクトルから最後尾のデータを除いたベクトルを引いて行っている。

設定条件は到着率λ = 1/10[回/秒。観測時間は分布形には影響を与えず、データ数にのみ関係する。今回はt = 1000秒で、データ数はλt – 1 = 99個。

また、理論上の指数分布の密度関数の曲線をヒストグラムに重ね合わせている。

lambda <- 1 / 10
t.obs <- 1000
num.data <- lambda * t.obs

org.data <- (runif(floor(num.data * 3)) * 3 - 1) * t.obs
data <- sort(org.data[(org.data >= 0) & (org.data < t.obs)])

interval <- data[-1] - data[-length(data)]

hist(interval, prob=TRUE, freq=FALSE)
curve(dexp(x,rate=lambda), add=TRUE)

lambda <- 1 / 10

t.obs <- 1000

num.data <- lambda * t.obs

org.data <- (runif(floor(num.data * 3)) * 3 - 1) * t.obs

data <- sort(org.data[(org.data >= 0) & (org.data < t.obs)])

interval <- data[-1] - data[-length(data)]

hist(interval, prob=TRUE, freq=FALSE)

curve(dexp(x,rate=lambda), add=TRUE)

この表示結果は以下のようになる。データ数は99だが、比較的よく指数分布の密度関数と整合している。

poisson-process-uniform-dist-interval100

到着数の分布

以下の手順で観測時間tの間の到着数のデータを用意する。

必要回数分、以下を繰り返す
- 観測時間をtとして、区間[–t, 2t)で乱数を発生
- 0以上、t未満のデータを除いたデータを得てソート
- その個数を数える

Rのコードは以下の通り。到着率はこれまでと同じ1/10、観測時間は100秒で、この観測時間内の期待到着数は10回だが、これがどの程度ばらつくかを確認するため、このデータを1000回発生させて、ヒストグラムを描かせている。

lambda <- 1 / 10
t.obs <- 100
num.data <- lambda * t.obs
n.loop <- 1000

arrivals <- rep(0, num.data)

for (i in 1:n.loop) {
  org.data <- (runif(floor(num.data * 3)) * 3 - 1) * t.obs
  data <- org.data[(org.data >= 0) & (org.data < t.obs)]
  arrivals[i] <- length(data)
}

hist(arrivals, prob=TRUE, xlim=c(0,20), breaks=seq(0,20,2.5))

lambda <- 1 / 10

t.obs <- 100

num.data <- lambda * t.obs

n.loop <- 1000

arrivals <- rep(0, num.data)

for (i in 1:n.loop) {

org.data <- (runif(floor(num.data * 3)) * 3 - 1) * t.obs

data <- org.data[(org.data >= 0) & (org.data < t.obs)]

arrivals[i] <- length(data)

}

hist(arrivals, prob=TRUE, xlim=c(0,20), breaks=seq(0,20,2.5))

到着率、観測時間が同じパラメータのPoisson分布もあわせて描いたのが以下のグラフ。

poisson-process-uniform-dist-poisson-n010

到着率を変えずに観測時間tを100→1000秒にした場合の分布は以下のようになる。

poisson-process-uniform-dist-poisson-n100

ここで縦軸に注意。頻度／確率のスケールが初めのものより小さくなっている。つまり、このグラフは最初のグラフに比べて、右の方へずれて、高さはぐっと低くなっている(この傾向はPoisson分布の傾向)。

以下に、パラメータλtのtをj変化させたときのヒストグラムを重ね合わせてみる。

generate <- function(dummy, lambda, t) {
  n <- lambda * t
  org.data <- (runif(floor(n * 3)) * 3 - 1) * t
  data <- org.data[(org.data >= 0) & (org.data < t)]
  return (length(data))
}

lambda <- 1 / 10
t.obs <- 100

arrivals1 <- sapply(rep(0, 1000), generate, lambda, 50)
arrivals2 <- sapply(rep(0, 1000), generate, lambda, 100)
arrivals3 <- sapply(rep(0, 1000), generate, lambda, 200)

xlm <- c(0, 35)
ylm <- c(0, 0.25)
brk <- seq(0, 35, 2.5)
hist(arrivals1, prob=TRUE, col="#ff000040", xlim=xlm, ylim=ylm, breaks=brk)
hist(arrivals2, prob=TRUE, col="#00ff0040", xlim=xlm, ylim=ylm, breaks=brk, add=TRUE)
hist(arrivals3, prob=TRUE, col="#0000ff40", xlim=xlm, ylim=ylm, breaks=brk, add=TRUE)

generate <- function(dummy, lambda, t) {

n <- lambda * t

org.data <- (runif(floor(n * 3)) * 3 - 1) * t

data <- org.data[(org.data >= 0) & (org.data < t)]

return (length(data))

}

lambda <- 1 / 10

t.obs <- 100

arrivals1 <- sapply(rep(0, 1000), generate, lambda, 50)

arrivals2 <- sapply(rep(0, 1000), generate, lambda, 100)

arrivals3 <- sapply(rep(0, 1000), generate, lambda, 200)

xlm <- c(0, 35)

ylm <- c(0, 0.25)

brk <- seq(0, 35, 2.5)

hist(arrivals1, prob=TRUE, col="#ff000040", xlim=xlm, ylim=ylm, breaks=brk)

hist(arrivals2, prob=TRUE, col="#00ff0040", xlim=xlm, ylim=ylm, breaks=brk, add=TRUE)

hist(arrivals3, prob=TRUE, col="#0000ff40", xlim=xlm, ylim=ylm, breaks=brk, add=TRUE)

poisson-process-uniform-dist-poisson-3params

Rによるポアソン過程のシミュレーション

2016-09-12 / tau / コメントする

概要

一様乱数を基にしたポアソン過程のシミュレーションは前にまとめたが、その時には表計算ソフトを使ったので操作性も悪く、限られたケースのみ計算したレベルだった。

その後、統計分析用のソフト”R“を少し勉強したので、より掘り下げた確認をしてみる。

前提条件と手法

平均すると10秒に1回、客が訪れる事象を考える。単位時間を1秒とすると、到着率は $\lambda = 1/10$ となる。この条件下で、以下のことを確認する。

一様乱数によったときの確率分布
- 時系列上での到着時刻の分布～一様分布
- 到着時間間隔の分布～指数分布
- 到着数の分布～Poisson分布
時刻制御(time driven)によったときの各種確率分布
- 同上
イベント制御(event driven)ときの各種確率分布
- 時系列上での到着時刻の分布～一様乱数
- 到着数の分布～Poisson分布

考え方

一様乱数による方法

下図のように、観測時間tの間で一度に一様乱数を発生させ、それを昇順にソートしたものを到着時刻の時系列データとする。

poisson-process-fig-uniform-dist

単に到着率λと観測時間tを掛けた平均到着数で乱数を発生させた場合、観測時間内の到着数が一定となってしまうため、観測時間と同じ時間幅で前後に余裕をとり、その中で一様乱数を発生させたうえで両端を切り落としている。

時刻制御とイベント制御

下図に、時刻制御(time driven)とイベント制御(event driven)の考え方の違いを比較して示している。

poisson-process-fig-time-and-event-driven

時刻制御については、観測時間を小さな時間間隔に区切って、区間ごとに到着確率に沿って到着の有無を決めながら、時刻を前に進めていく。

イベント制御の場合は、ポアソン過程で到着時間間隔が指数分布に従うことを利用して、指数乱数を発生させながら順次に到着時刻を算出していく。

逆関数による乱数の発生

2016-09-12 / tau / コメントする

問題

確率変数 $X$ が確率分布 $F(X)$ に、確率変数 $U$ が $[0, 1)$ 上の一様分布に従うとする。このとき $F^{-1} (U)$ は確率分布 $F$ に従う。

下図にもあるように、確率分布関数が立っているところ、すなわち確率密度の高いところが高くなるような乱数が生成されることになるので、直感的にわかりやすい。

stat-inverse-function-probability-number

証明

Uが一様分布に従うことを以下のように表す。

(1) $\begin{equation*} P(U \le u) = u \quad (0 \le u < 1) \end{equation*}$

確率分布関数 $F(X)$ は単調増加で、その逆関数も単調増加だから、

(2) $\begin{equation*} U \le u \Leftrightarrow F^{-1} (U) \le F^{-1} (u) \end{equation*}$

これより、

(3) $\begin{equation*} P(U \le u) = P(F^{-1}(U) \le F^{-1}(u)) = u \end{equation*}$

ここで $F^{-1}(u) = x$ とおくと、 $u = F(x)$ だから、

(4) $\begin{equation*} P(F^{-1}(U) \le x) = F(x) \end{equation*}$

すなわち確率変数 $F^{-1}$ が確率分布 $F(x)$ に従うことを意味している。

指数分布の例

指数関数の確率分布関数は以下の形をとる。

(5) $\begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}$

これの逆関数系は以下のとおり。

(6) $\begin{equation*} F^{-1}(U) = - \frac{1}{\lambda} \ln( 1 - u) \end{equation*}$

上式の $u$ に一様乱数列を入れることで、計算結果は指数分布に従う乱数列として得られる。

統計分析言語Rで確認したところ、一様乱数からきれいな指数乱数が得られている。

exprand <- function(dummy) return(- 1 * log(1 - runif(1)))

data <- rep(0, 100)
data <- sapply(data, exprand)

hist(data, freq=FALSE)
curve(dexp(x, rate=1), add=TRUE)

exprand <- function(dummy) return(- 1 * log(1 - runif(1)))

data <- rep(0, 100)

data <- sapply(data, exprand)

hist(data, freq=FALSE)

curve(dexp(x, rate=1), add=TRUE)

stat-inverse-function-exponential-random-number

R – sapplyについて

2016-09-11 / tau / コメントする

ベクトル演算とsapplyの違い

ベクトルの各要素に関数を作用させたいとき、普通は次のようにする。

> f <- function(x) x*x
> f(seq(1, 5))
[1]  1  4  9 16 25

> f <- function(x) x*x

> f(seq(1, 5))

[1] 1 4 9 16 25

これを、sapplyを使って次のようにも書ける。

> f <- function(x) x*x
> sapply(seq(1, 5), f)
[1]  1  4  9 16 25

> f <- function(x) x*x

> sapply(seq(1, 5), f)

[1] 1 4 9 16 25

一見すると何ら違いはないように見えるが、次のような場合に違いが出てくる。

> f <- function(x) x * runif(1)
> f(rep(1, 5))
[1] 0.7131735 0.7131735 0.7131735 0.7131735 0.7131735
> sapply(rep(1, 5), f)
[1] 0.56394702 0.71369838 0.09517609 0.72681560 0.47276722

> f <- function(x) x * runif(1)

> f(rep(1, 5))

[1] 0.7131735 0.7131735 0.7131735 0.7131735 0.7131735

> sapply(rep(1, 5), f)

[1] 0.56394702 0.71369838 0.09517609 0.72681560 0.47276722

ベクトル演算の場合は、全ての要素に対して同じ演算結果が適用されるる。このためrunif(1)が1度だけ計算され、各要素にその結果が適用されるので、全要素が同じ値になる。

sapplyの場合は、各要素に対して毎回演算が行われる、このため各要素ごとにrunif(1)が計算されて適用されるので、各要素の値が異なる。

各要素に新規の計算結果を入れたいとき

各要素の初期値と無関係に要素に計算結果を適用したいと意図したとき、関数にダミー変数を書いておいて処理する。

例えば以下の例では、5つの要素に新たな乱数を発生させてセットしようとしている。

> f <- function(dummy) runif(1)
> sapply(rep(0, 5), f)
[1] 0.2031135 0.4134661 0.9572596 0.6462498 0.2886842
> f(rep(0, 5))
[1] 0.4594526
> rep(f(0), 5)
[1] 0.7015942 0.7015942 0.7015942 0.7015942 0.7015942

> f <- function(dummy) runif(1)

> sapply(rep(0, 5), f)

[1] 0.2031135 0.4134661 0.9572596 0.6462498 0.2886842

> f(rep(0, 5))

[1] 0.4594526

> rep(f(0), 5)

[1] 0.7015942 0.7015942 0.7015942 0.7015942 0.7015942

sapplyの場合は期待通りの結果。この場合は関数に引数が要求されるので、dummyという引数を与えている。

関数の引数にベクトルを入れると、その引数に対して1回だけ乱数を発生させるので、結果は1個の数値。

rep()関数の引数にf()を適用すると、1回だけ発生した乱数がすべての要素に適用されている。

複数の引数を持つ関数の場合

次の例は、各要素それぞれに0～2の範囲の乱数をセットしている。

> f <- function(dummy, a) runif(1) * a
> sapply(rep(0, 5), f, 2)
[1] 0.8868690 1.0057694 1.3814147 1.4157728 0.2052112

> f <- function(dummy, a) runif(1) * a

> sapply(rep(0, 5), f, 2)

[1] 0.8868690 1.0057694 1.3814147 1.4157728 0.2052112

sapplyに渡す関数が2つ以上の引数を持つときは、関数に続けて残りの引数を渡せばよい。

CoffeeScript – コマンドライン引数

2016-09-08 / tau / コメントする

process.argv[n]にコマンドラインの入力が格納される。

argv[0]　コマンド(“coffee”)
argv[1]　ファイル名(“パス/ファイル名”)
argv[2]　1つ目の引数
・・・

指定していない引数を参照するとundefined

console.log(process.argv[0]) # coffee
console.log(process.argv[1]) # パス/ファイル名
console.log(process.argv[2]) # 第1引数
console.log(process.argv[3]) # 第2引数

console.log(process.argv[0]) # coffee

console.log(process.argv[1]) # パス/ファイル名

console.log(process.argv[2]) # 第1引数

console.log(process.argv[3]) # 第2引数

Collatzの問題

2016-09-08 / tau / コメントする

ドイツのLothar Collatzという数学者が1937年に提示したとのことで、まだ証明がされていないらしい。予想は以下のようにシンプル。

任意の自然数の初期値nに対して、以下の操作を繰り返すことにより、有限回の操作で必ず1に達する。

nが偶数の場合、2で割る
nが奇数の場合、3倍して1を足す

CoffeeScriptによるコードの例

n = parseInt(process.argv[2])

until n == 1
  console.log(n)
  if n % 2 == 0
    n = n // 2
  else
    n = n * 3 + 1

console.log(n)

n = parseInt(process.argv[2])

until n == 1

console.log(n)

if n % 2 == 0

n = n // 2

else

n = n * 3 + 1

console.log(n)

いくつかの初期値に対するnの変化

1 -> 1
2 -> 2 1
3 -> 3 10 5 16 8 4 2 1
4 -> 4 2 1
5 -> 5 16 8 4 2 1

1 -> 1

2 -> 2 1

3 -> 3 10 5 16 8 4 2 1

4 -> 4 2 1

5 -> 5 16 8 4 2 1

R – ヒストグラム

2016-09-08 / tau / コメントする

基本形

ヒストグラムは、ベクトルでデータと階級を与えて表示させる。

data <- c(42,68,57,48,75,81,65,93,51,66,79,69,63,80,53)
hist(data)

1 2	data <- c(42,68,57,48,75,81,65,93,51,66,79,69,63,80,53) hist(data)

r-hist-ex-smp

オプション

階級値の指定と度数／頻度の選択

breaks属性に指定したベクトルで階級値を指定
ylim属性に指定したベクトルで縦軸の範囲を指定
prob=TRUEを指定することで縦軸を度数から頻度に変更

data <- c(42,68,57,48,75,81,65,93,51,66,79,69,63,80,53)
ranks <- seq(40,100,15)
density <- c(0, 0.03)
hist(data, breaks=ranks, ylim=density, prob=TRUE)

data <- c(42,68,57,48,75,81,65,93,51,66,79,69,63,80,53)

ranks <- seq(40,100,15)

density <- c(0, 0.03)

hist(data, breaks=ranks, ylim=density, prob=TRUE)

r-hist-ex-smp-axis

ラベルや色の指定

main属性とxlab属性に文字列を指定して、表題と横軸のラベルを設定
col属性でヒストグラムの色指定が可能

data <- c(42,68,57,48,75,81,65,93,51,66,79,69,63,80,53)
hist(data, main="Data", xlab="Range", col="#008888")

1 2	data <- c(42,68,57,48,75,81,65,93,51,66,79,69,63,80,53) hist(data, main="Data", xlab="Range", col="#008888")

r-hist-ex-smp-lblcol

複数グラフ

横に並べる

data1 <- c(42,68,57,48,75,81,65,93,51)
data2 <- c(66,79,69,63,80,53)

par(mfrow=c(1,2))

ranks <- seq(40,100,15)
hist(data1, breaks=ranks)
hist(data2, breaks=ranks)

data1 <- c(42,68,57,48,75,81,65,93,51)

data2 <- c(66,79,69,63,80,53)

par(mfrow=c(1,2))

ranks <- seq(40,100,15)

hist(data1, breaks=ranks)

hist(data2, breaks=ranks)

r-hist-ex-col2

縦に並べる

data1 <- c(42,68,57,48,75,81,65,93,51)
data2 <- c(66,79,69,63,80,53)

par(mfrow=c(2,1))

ranks <- seq(40,100,15)
hist(data1, breaks=ranks)
hist(data2, breaks=ranks)

data1 <- c(42,68,57,48,75,81,65,93,51)

data2 <- c(66,79,69,63,80,53)

par(mfrow=c(2,1))

ranks <- seq(40,100,15)

hist(data1, breaks=ranks)

hist(data2, breaks=ranks)

r-hist-ex-row2

関数曲線との重ね合わせ

ヒストグラムの定義域の数値をそのまま使い、関数を渡して描画させることができる。

data <- runif(100)
hist(data, freq=FALSE)
curve(x*2, add=TRUE, col="blue", lwd=2)
curve(-log(x), add=TRUE, col="red", lwd=3)

data <- runif(100)

hist(data, freq=FALSE)

curve(x*2, add=TRUE, col="blue", lwd=2)

curve(-log(x), add=TRUE, col="red", lwd=3)

要点は以下の通り

hist()関数でfreq=FALSEを指定
curve()関数の第一引数で描画したい関数を指定(独立変数をxとする)
curve()関数でadd=TRUEを指定

r-hist-ex-superimpose

これを利用して、ヒストグラムに確率密度関数を重ねて描画することができる。

R – plot()

2016-09-08 / tau / コメントする

概要

Rの高水準作図関数で、タイプ指定で散布図、折れ線グラフなど様々なグラフを描くことができる。

基本形

数字の対を与えて散布図を描く。

x <- seq(0, 1, 0.1)
y <- x ^ 2
plot(x, y)

x <- seq(0, 1, 0.1)

y <- x ^ 2

plot(x, y)

r-plot-basic

タイプ指定

plot()のタイプ

引数	機能
`type="p"`	点プロット(デフォルト)
`type="l"`	折れ線グラフ
`type="b"`	点と線のプロット
`type="c"`	“b”で点を描かないプロット
`type="o"`	点プロットと線プロットの重ね描き
`type="h"`	各点からx軸まで垂線を描く
`type="s"`	左側の値から右にステップ表示
`type="S"`	右側の値から左にステップ表示
`type="n"`	軸だけ描く(その後低水準関数でプロット)

折れ線グラフ

例えばtype指定によって折れ線グラフを描ける。

x <- seq(0, 1, 0.1)
y <- x ^ 2
plot(x, y, type="l")

x <- seq(0, 1, 0.1)

y <- x ^ 2

plot(x, y, type="l")

r-plot-type-l

関数を直接与える場合

関数と定義域を与えて、直接その形を描ける。

plot(sin, -pi, pi)

1	plot(sin, -pi, pi)

r-plot-function-sin

定義した関数を渡すこともできる。

para <- function(x) x^2
plot(para, -1, 1, asp=1, pos=0)

1 2	para <- function(x) x^2 plot(para, -1, 1, asp=1, pos=0)

r-plot-function-user

asp=1は縦軸と横軸のスケール比を1:1に設定する引数
pos=0はゼロで軸が交わるようにする引数

イベント制御による分析

到着イベントの時系列

到着数の分布

関連リンク

時刻制御による分析

到着イベントの時系列

到着時間間隔の分布

到着数の分布

関連リンク

一様乱数に基づく分析

到着時刻の分布

到着時間間隔の分布

到着数の分布

関連リンク

概要

前提条件と手法

考え方

一様乱数による方法

時刻制御とイベント制御

関連リンク

問題

証明

指数分布の例

ベクトル演算とsapplyの違い

各要素に新規の計算結果を入れたいとき

複数の引数を持つ関数の場合

基本形

オプション

階級値の指定と度数／頻度の選択

ラベルや色の指定

複数グラフ

横に並べる

縦に並べる

関数曲線との重ね合わせ

概要

基本形

タイプ指定

plot()のタイプ

折れ線グラフ

関数を直接与える場合