matplotlib.patches – 図形の描画

2020-04-30 / tau / コメントする

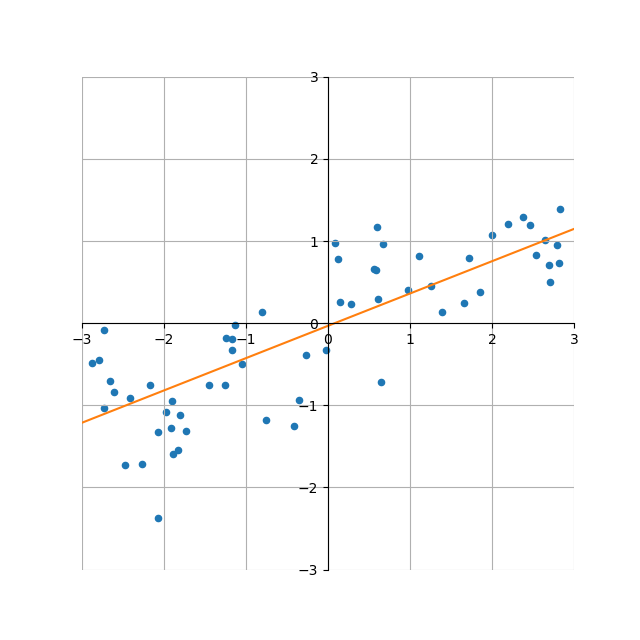
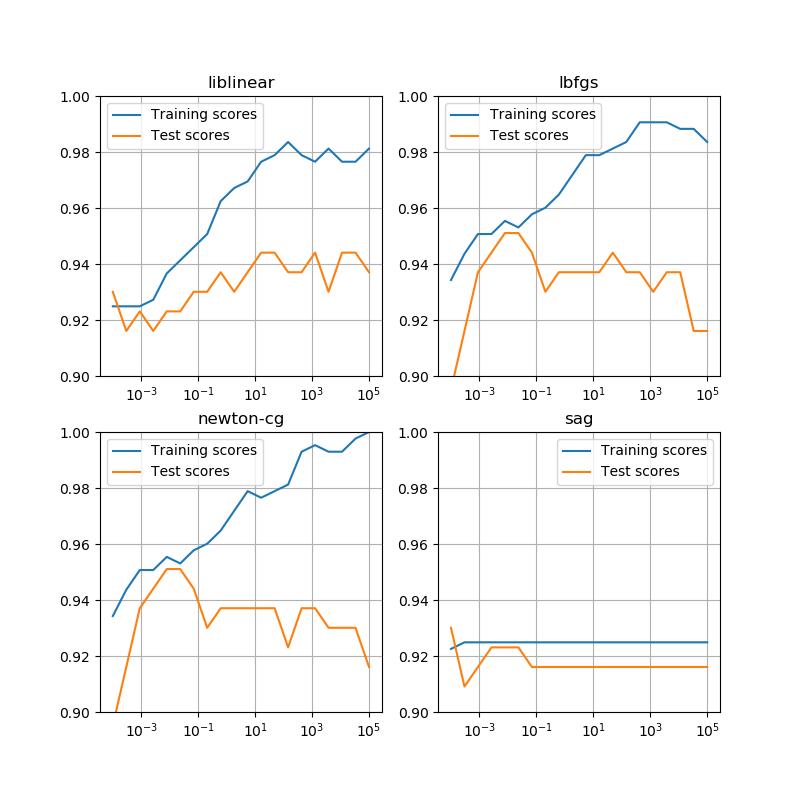
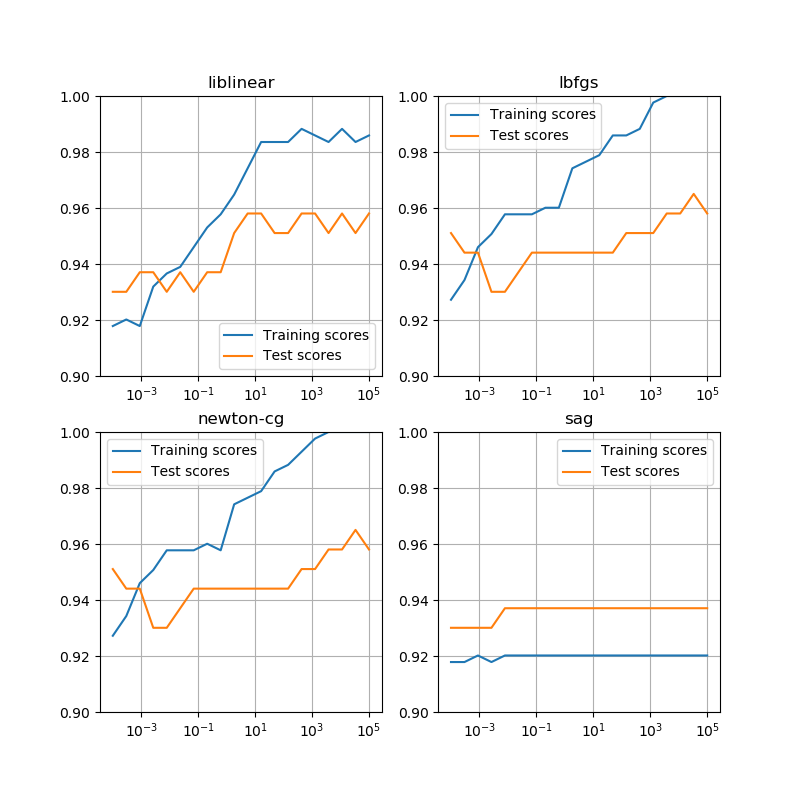
概要

matplotlib.patchesパッケージに様々な図形クラスが準備されていて、Axesのadd_patch()メソッドでそれらのオブジェクトを加えていく。

import matplotlib.pyplot as plt
import matplotlib.patches as patch

fig, ax = plt.subplots()

circ = patch.Circle(xy=(3, 3), radius=2, ec='b', fc='gray')
elli = patch.Ellipse(xy=(2, 1), width=2, height=1, ec='g', fill=False, angle=10)
rect = patch.Rectangle(xy=(1, 2), width=3, height=2, ec='b', fc='w', angle=30)

ax.add_patch(circ)
ax.add_patch(elli)
ax.add_patch(rect)

ax.set_xlim(0, 6)
ax.set_ylim(0, 6)
ax.set_aspect('equal')

plt.show()

import matplotlib.pyplot as plt

import matplotlib.patches as patch

fig, ax = plt.subplots()

circ = patch.Circle(xy=(3, 3), radius=2, ec='b', fc='gray')

elli = patch.Ellipse(xy=(2, 1), width=2, height=1, ec='g', fill=False, angle=10)

rect = patch.Rectangle(xy=(1, 2), width=3, height=2, ec='b', fc='w', angle=30)

ax.add_patch(circ)

ax.add_patch(elli)

ax.add_patch(rect)

ax.set_xlim(0, 6)

ax.set_ylim(0, 6)

ax.set_aspect('equal')

plt.show()

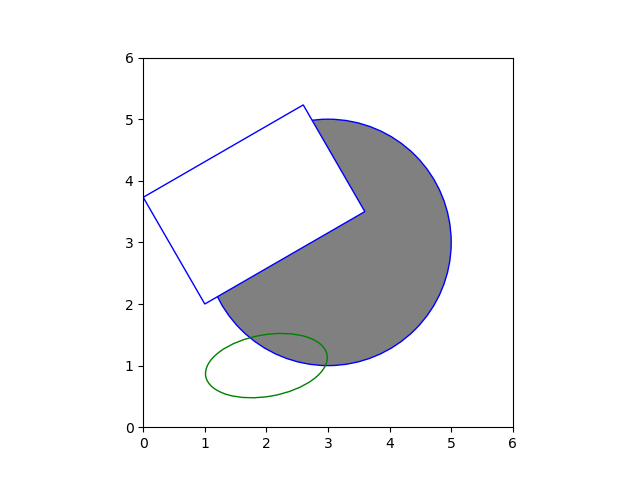
各種図形

以下の点は各図形において共通

ほとんどの図形は引数xyで基準点のx座標とy座標をタプルで与える
edgecolor/ecで外枠の色、facecolor/fcで塗りつぶし色を指定する
fill=True/Falseで塗りつぶしの有無を指定する
angleで傾きの角度を指定できる図形がある

Circle(xy[, radius=5]): 中心点を指定して円を描く。
Ellipse(xy, width, height[, angle]): 中心点と幅・高さを指定して楕円を描く。
Rectangle(xy, width, height[, angle]): 左下の点と幅・高さを指定して楕円を描く。
CirclePolygon(x, y, rasius=5, resolution=20): 多角形を描画。辺／頂点の数をresolutionで指定する。
Polygon(xy, closed=True): 複数の点を指定して図形を描画する。xyはNx2配列(xy座標を要素とした2次元配列)。closedをFalseに指定すると図形の最初の点と最後の点を結ばない。
Arc(xy, width, height[, angle, theta1, theta2]): 楕円の一部の弧を描く。扇形に中を塗りつぶすことはできない。
Wedge(center, r, theta1, theta2[, width=None]): 円の一部を切出した図形を描く。widhを指定すると中心からその長さだけ除かれて描かれる。

Arrow(x, y, dx, dy[, width, ...]): 矢印を描画する。
FancyArrow(x, y, dx, dy[, width, ...]): 鏃を片側だけにしたり、鏃の大きさや形を設定したりできる。

arg max

2020-04-29 / tau / コメントする

maxが関数の最大値を意味するのに対して、arg maxは関数が最大値をとる場合の定義域を意味する。

(1) $\begin{align*} &\max x(4-x) = 4\\ &\arg \max x(4-x) = 2 \end{align*}$

定義域を指定する場合。

(2) $\begin{align*} &{\arg \max}_{-1 \le x \le 0} \, x(x + 1)(x - 1) = -\frac{1}{\sqrt{3}}\\ &\max_{-1 \le x \le 0} x(x + 1)(x - 1) = \frac{2\sqrt{3}}{9} \end{align*}$

本来arg maxは関数が最大値をとる定義域の集合を表す。

(3) $\begin{equation*} {\arg \max}_{0 \le x \le 4\pi} \, \cos x = \{ 0, 2\pi, 4\pi\} \end{equation*}$

Ridge回帰の理解

2020-04-26 / tau / コメントする

定義

Ridge回帰は多重回帰の損失関数に罰則項としてL2正則化項を加味する。正則化の意味についてはこちらに詳しくまとめている。

L2ノルムは原点からのユークリッド距離。

(1) $\begin{equation*} \| \boldsymbol{w} \| _2 = \sqrt{w_1 ^2 + \cdots + w_m^2} \end{equation*}$

ただしリッジ回帰では、根号の中の二乗項で計算する。

(2) $\begin{equation*} \mathrm{minimize} \quad \sum_{i=1}^n (y_i - \hat{y}_i) + \alpha \sum_{j=1}^m w_j^2 \end{equation*}$

定式化

最小化すべき関数は、

(3) $\begin{align*} L &= \sum_{i=1}^n ( \hat{y}_i - y_i )^2 + \alpha ({w_1}^2 + \cdots + {w_2}^2) \\ &= \sum ( w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i )^2 + \alpha ({w_1}^2 + \cdots + {w_m}^2) \end{align*}$

重み係数を計算するために、それぞれで偏微分してゼロとする。

(4) $\begin{align*} \frac{\partial L}{\partial w_0} &= 2 \sum (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) = 0 \\ \frac{\partial L}{\partial w_1} &= 2 \sum x_{1i} (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) + 2 \alpha w_1 = 0 \\ \vdots\\ \frac{\partial L}{\partial w_m} &= 2 \sum x_{mi} (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) + 2 \alpha w_m = 0\\ \end{align*}$

その結果得られる連立方程式は以下の通り。

(5) $\begin{align*} n w_0 + w_1 \sum x_{1i} + \cdots + w_m \sum x_{mi} &= \sum y_i \\ w_0 \sum x_{1i} + w_1 \left( \sum {x_{1i}}^2 + \alpha \right) + \cdots + w_m \sum x_{1i} x_{mi} &= \sum x_{1i} y_i \\ \vdots \\ w_0 \sum x_{mi} + w_1 \sum x_{1i} x_{mi} + \cdots+ w_m \left( \sum {x_{mi}}^2 + \alpha \right) &= \sum x_{mi} y_i \\ \end{align*}$

ここでそれぞれの和を記号Sと添字で表し、さらに行列表示すると以下の通り。

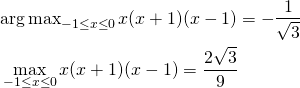
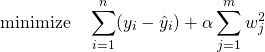
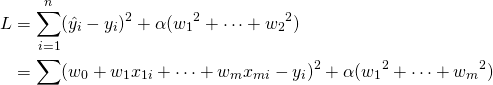
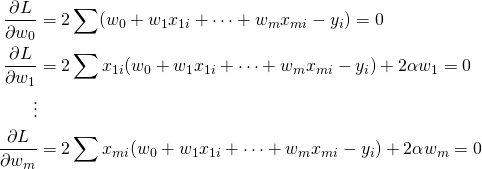
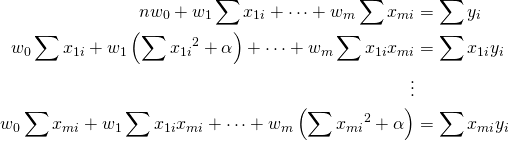
(6) $\begin{equation*} \left[ \begin{array}{cccc} n & S_1 & \cdots & S_m \\ S_1 & S_{11} + \alpha & & S_{1m} \\ \vdots & \vdots & & \vdots \\ S_m & S_{m1} & \cdots & S_{mm} + \alpha \end{array} \right] \left[ \begin{array}{c} w_0 \\ w_1 \\ \vdots \\ w_m \end{array} \right] = \left[ \begin{array}{c} S_y \\S_{1y} \\ \vdots \\ S_{my} \end{array} \right] \end{equation*}$

ここで $w_0$ を消去して、以下の連立方程式を得る。

(7) $\begin{align*} &\left[ \begin{array}{ccc} ( S_{11} + \alpha ) - \dfrac{{S_1}^2}{n} & \cdots & S_{1m} - \dfrac{S_1 S_m}{n} \\ \vdots & & \vdots \\ S_{m1} - \dfrac{S_m S_1}{n} & \cdots & ( S_{mm} + \alpha )- \dfrac{{S_2}^2}{n} \end{array} \right] \left[ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array} \right] \\&= \left[ \begin{array}{c} S_{1y} - \dfrac{S_1 S_y}{n} \\ \vdots \\ S_{my} - \dfrac{S_m S_y}{n} \end{array} \right] \end{align*}$

これを分散・共分散で表すと、

(8) $\begin{equation*} \left[ \begin{array}{ccc} V_{11} + \dfrac{\alpha}{n} & \cdots & V_{1m} \\ \vdots & & \vdots \\ V_{m1} & \cdots & V_{mm} + \dfrac{\alpha}{n} \end{array} \right] \left[ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array} \right] = \left[ \begin{array}{c} V_{1y} \\ \vdots \\ V_{my} \end{array} \right] \end{equation*}$

ここで仮に、x_jiとx_kiが完全な線形関係にある場合を考えてみる。 $x_j = a x_i + b$ とすると、分散・共分散の性質より、

(9) $\begin{equation*} V_{jj} = a^2V_{ii}, \; V_{ji} = V_{ij} = aV_{ii}, \; V_{jk} = V_{kj} = aV_{ji} = aV_{ij} \end{equation*}$

このような場合、通常の線形回帰は多重共線性により解を持たないが、式(8)に適用すると係数行列は以下のようになる。

(10) $\begin{align*} \left[ \begin{array}{ccccccc} V_{11} + \dfrac{\alpha}{n} & \cdots & V_{1i} & \cdots & aV_{1i} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} + \dfrac{\alpha}{n} & \cdots & aV_{ii} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ aV_{i1} & \cdots & aV_{ii} & \cdots & a^2V_{ii} + \dfrac{\alpha}{n} & \cdots & aV_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & aV_{mi} & \cdots & V_{mm} + \dfrac{\alpha}{n} \end{array} \right] \end{align*}$

対角要素にαが加わることで、多重共線性が強い場合でも係数行列の行列式は正則となり、方程式は解を持つ。また正則化の効果より、αを大きな値とすることによって係数の値が小さく抑えられる。

行列による表示

式(3)の損失関数を、n個のデータに対する行列で表示すると以下の通り（重回帰の行列表現はこちらを参照）。

(11) $\begin{align*} L &= \left( \boldsymbol{Xw} - \boldsymbol{y} \right)^T \left( \boldsymbol{Xw} - \boldsymbol{y} \right) + \alpha \boldsymbol{w}^T \boldsymbol{w} \\ &= \boldsymbol{w}^T \boldsymbol{X}^T \boldsymbol{Xw} - 2\boldsymbol{y}^T \boldsymbol{Xw} + \boldsymbol{y}^T \boldsymbol{y} + \alpha \boldsymbol{w}^T \boldsymbol{w} \end{align*}$

これをwで微分してLを最小とする値を求める。

(12) $\begin{gather*} \frac{dL}{d\boldsymbol{w}} = 2\boldsymbol{X}^T \boldsymbol{Xw} - 2 \boldsymbol{X}^T \boldsymbol{y} + 2 \alpha \boldsymbol{w} = \boldsymbol{0} \\ \boldsymbol{w} = \left( \boldsymbol{X}^T \boldsymbol{X} + \alpha \boldsymbol{I} \right)^{-1} \boldsymbol{X}^T \boldsymbol{y} \end{gather*}$

行列式の定義

2020-04-23 / tau / コメントする

定義式

(1) $\begin{align*} |\boldsymbol{A}| &= \sum_{\sigma \in S_n} {\rm sgn}(\sigma) \prod_{i=1}^n a_{i\sigma(i)} \\ &= \sum_{\sigma \in S_n} {\rm sgn}(\sigma) a_{1\sigma(1)} a_{2\sigma(2)} \cdots a_{n\sigma(n)} \end{align*}$

計算例

次数2の場合

(2) $\begin{align*} |\boldsymbol{A}| &= \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \\ &= {\rm sgn}(\sigma_1)a_{1\sigma_1(1)}a_{2\sigma_1(2)} + {\rm sgn}(\sigma_2)a_{1\sigma_2(1)}a_{2\sigma_2(2)} \end{align*}$

ここで、

(3) $\begin{equation*} \sigma_1 = \left( \begin{array}{cc} 1 & 2 \\ 1 & 2 \end{array} \right) ,\quad \sigma_2 = \left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \end{array} \right) \end{equation*}$

(4) $\begin{equation*} {\rm sgn}(\sigma_1) = 1 ,\quad {\rm sgn}(\sigma_2) = -1 \end{equation*}$

(5) $\begin{equation*} \sigma_1(1) = 1 ,\; \sigma_1(2) = 2 ,\; \sigma_2(1) = 2 ,\; \sigma_2(2) = 1 \end{equation*}$

したがって行列式の値は、

(6) $\begin{equation*} |\boldsymbol{A}| = a_{11}a_{22} - a_{12}a_{21} \end{equation*}$

次数3の場合

(7) $\begin{align*} |\boldsymbol{A}| =& \left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| \\ =& {\rm sgn}(\sigma_1)a_{1\sigma_1(1)}a_{2\sigma_1(2)}a_{3\sigma_1(3)} + {\rm sgn}(\sigma_2)a_{1\sigma_2(1)}a_{2\sigma_2(2)}a_{3\sigma_2(3)}\\ &{\rm sgn}(\sigma_3)a_{1\sigma_3(1)}a_{2\sigma_3(2)}a_{3\sigma_3(3)} + {\rm sgn}(\sigma_4)a_{1\sigma_4(1)}a_{2\sigma_4(2)}a_{4\sigma_4(3)}\\ &{\rm sgn}(\sigma_5)a_{1\sigma_5(1)}a_{2\sigma_5(2)}a_{3\sigma_5(3)} + {\rm sgn}(\sigma_6)a_{1\sigma_6(1)}a_{2\sigma_6(2)}a_{4\sigma_6(3)} \end{align*}$

ここで、

(8) $\begin{gather*} \sigma_1 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \end{array} \right) ,\quad \sigma_2 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \end{array} \right) \\ \sigma_3 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \end{array} \right) ,\quad \sigma_4 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array} \right) \\ \sigma_5 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \end{array} \right) ,\quad \sigma_6 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array} \right) \end{gather*}$

(9) $\begin{equation*} \begin{array}{ll} {\rm sgn}(\sigma_1) = \phantom{-}1 ,& {\rm sgn}(\sigma_2) = -1 \\ {\rm sgn}(\sigma_3) = -1 ,& {\rm sgn}(\sigma_4) = \phantom{-}1 \\ {\rm sgn}(\sigma_5) = \phantom{-}1 ,& {\rm sgn}(\sigma_6) = -1 \end{array} \end{equation*}$

(10) $\begin{gather*} \sigma_1(1) = 1 ,\; \sigma_1(2) = 2 ,\; \sigma_1(3) = 3 \\ \sigma_2(1) = 1 ,\; \sigma_2(2) = 3 ,\; \sigma_2(3) = 2 \\ \sigma_3(1) = 2 ,\; \sigma_3(2) = 1 ,\; \sigma_3(3) = 3 \\ \sigma_4(1) = 2 ,\; \sigma_2(2) = 3 ,\; \sigma_4(3) = 1 \\ \sigma_5(1) = 3 ,\; \sigma_5(2) = 1 ,\; \sigma_5(3) = 2 \\ \sigma_6(1) = 3 ,\; \sigma_6(2) = 2 ,\; \sigma_6(3) = 1 \end{gather*}$

したがって行列式の値は、

(11) $\begin{align*} |\boldsymbol{A}| &= a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} \\ &- a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} \\ &+ a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} \end{align*}$

ベクトル・行列を含む微分

2020-04-19 / tau / 20件のコメント

記号の定義

以下の記号で統一的に定義しておく。ベクトルは原則として列ベクトル表示を標準とする。

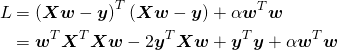
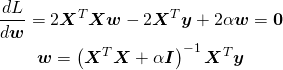
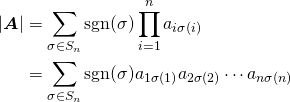
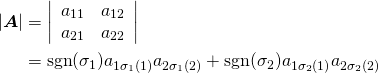
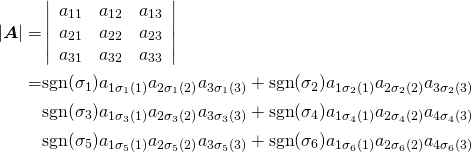
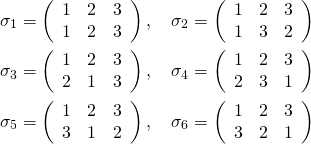
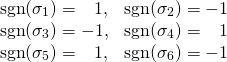
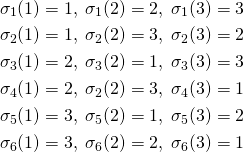
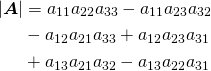
(1) $\begin{equation*} \boldsymbol{x} = \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \\ \end{array} \right] \end{equation*}$

(2) $\begin{equation*} \boldsymbol{X} = \left[ \begin{array}{ccc} x_{11} & \ldots & x_{1n} \\ \vdots & x_{ij} & \vdots \\ x_{m1} & \ldots & x_{mn} \end{array} \right] \end{equation*}$

(3) $\begin{equation*} f(\boldsymbol{x}) = f(x_1, \ldots, x_m) \end{equation*}$

(4) $\begin{equation*} \boldsymbol{f}(x) = \left[ \begin{array}{c} f_1(x) \\ \vdots \\ f_n(x) \end{array} \right] \end{equation*}$

(5) $\begin{equation*} \boldsymbol{f}(\boldsymbol{x}) =\ \left[ \begin{array}{c} f_1(x_1, \ldots, x_n) \\ \vdots \\ f_m(x_1, \ldots, x_n) \end{array} \right] \end{equation*}$

(6) $\begin{equation*} \boldsymbol{F}(x) = \left[ \begin{array}{ccc} F_{11}(x) & \ldots & F_{1n}(x) \\ \vdots & F_{ij} & \vdots \\ F_{m1}(x) & \ldots & F_{mn}(x) \\ \end{array} \right] \end{equation*}$

ベクトル・行列をスカラーで微分

これらは素直にベクトル・行列の要素を微分すればよい。

(7) $\begin{equation*} \frac{d \boldsymbol{f}(x)}{dx} = \left[ \begin{array}{c} \dfrac{d f_1(x)}{dx} \\ \vdots \\ \dfrac{d f_n(x)}{dx} \end{array} \right] \end{equation*}$

(8) $\begin{equation*} \frac{d \boldsymbol{F}(x)}{dx} = \left[ \begin{array}{ccc} \dfrac{dF_{11}(x)}{dx} & \ldots & \dfrac{dF_{1n}(x)}{dx} \\ \vdots & \dfrac{dF_{ij}(x)}{dx} & \vdots \\ \dfrac{dF_{m1}(x)}{dx} & \ldots & \dfrac{dF_{mn}(x)}{dx} \end{array} \right] \end{equation*}$

スカラーをベクトルで微分

スカラーを $\mathbb{R}^n$ のベクトルで微分すると、同じ次数のベクトルになる。

(9) $\begin{equation*} \frac{df(\boldsymbol{x})}{d\boldsymbol{x}} = \left[ \begin{array}{c} \dfrac{\partial f}{\partial x_1} \\ \vdots \\ \dfrac{\partial f}{\partial x_m} \end{array} \right] \end{equation*}$

これは便宜的に偏微分係数を要素とするベクトルを導入して以下のように考えるとよい。

(10) $\begin{equation*} \frac{d}{d\boldsymbol{x}}f(\boldsymbol{x}) = \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_m} \end{array}\right] f(\boldsymbol{x}) \end{equation*}$

スカラーを行列で微分

スカラーを $\mathbb{R}^m\times\mathbb{R}^n$ の行列で微分すると、同じ次元・次数の行列になる。

(11) $\begin{equation*} \frac{df(\boldsymbol{X})}{d\boldsymbol{X}} = \left[ \begin{array}{ccc} \dfrac{\partial f}{\partial x_{11}} & \ldots & \dfrac{\partial f}{\partial x_{1n}} \\ \vdots & \dfrac{\partial f}{\partial x_{ij}} & \vdots \\ \dfrac{\partial f}{\partial x_{m1}} & \ldots & \dfrac{\partial f}{\partial x_{mn}} \\ \end{array} \right] \end{equation*}$

これは便宜的に以下のように考えるとよい。

(12) $\begin{equation*} \frac{d}{d\boldsymbol{X}} f(\boldsymbol{X}) = \\ \left[ \begin{array}{ccc} \dfrac{\partial}{\partial x_{11}} & \ldots & \dfrac{\partial}{\partial x_{1n}} \\ \vdots & \dfrac{\partial}{\partial x_{ij}} & \vdots \\ \dfrac{\partial}{\partial x_{m1}} & \ldots & \dfrac{\partial}{\partial x_{mn}} \\ \end{array} \right] f(\boldsymbol{X}) \end{equation*}$

ベクトルをベクトルで微分

この場合、微分する変数側を行ベクトルとするか、微分される関数側を行ベクトルとするか2通りの表現があるが、ここでは関数側を行ベクトルとする。

(13) $\begin{equation*} \frac{d\boldsymbol{f}(\boldsymbol{x})^T}{d\boldsymbol{x}} = \left[ \begin{array}{ccc} \dfrac{\partial f_1}{\partial x_1} & \ldots & \dfrac{\partial f_n}{\partial x_1} \\ \vdots & \dfrac{\partial f_j}{\partial x_i} & \vdots \\ \dfrac{\partial f_1}{\partial x_m} & \ldots & \dfrac{\partial f_n}{\partial x_m} \\ \end{array} \right] \end{equation*}$

これは(10)で導入した偏微分係数ベクトルを導入して、便宜的に以下のように考えるとよい。

(14) $\begin{equation*} \frac{d}{d\boldsymbol{x}} \boldsymbol{f}(\boldsymbol{x})^T = \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\parial}{\partial x_m} \end{array} \right] [ f_1(\boldsymbol{x}) \; \ldots \; f_n(\boldsymbol{x}) ] = \left[ \begin{array}{ccc} \dfrac{\partial f_1}{\partial x_1} & \cdots & \dfrac{\partial f_n}{\partial x_1} \\ & \dfrac{\partial f_j}{\partial x_i} &\\ \dfrac{\partial f_1}{\partial x_m} & \cdots & \dfrac{\partial f_n}{\partial x_m} \end{array} \right] \end{equation*}$

公式

一般形

単位行列

ベクトルを同じベクトルで微分すると、単位ベクトルではなく単位行列になる。

(15) $\begin{equation*} \frac{d\boldsymbol{x}}{d\boldsymbol{x}} = \boldsymbol{I} \end{equation*}$

合成関数

スカラーの合成関数と似ているが、イメージと積の順番が逆で、この順番は変えられない。

(16) $\begin{align*} \frac{df(\boldsymbol{u}(\boldsymbol{x}))}{d\boldsymbol{x}} = \frac{d\boldsymbol{u}(\boldsymbol{x})^T}{d\boldsymbol{x}} \frac{df(\boldsymbol{u})}{d\boldsymbol{u}} \\ \end{align*}$

これは以下のように確認できる。

(17) $\begin{align*} \frac{df}{dx_i} &= \frac{\partial f}{\partial u_1}\frac{\partial u_1}{\partial x_i} + \cdots + \frac{\partial f}{\partial u_j}\frac{\partial u_j}{\partial x_i} + \cdots + \frac{\partial f}{\partial u_n}\frac{\partial u_n}{\partial x_i} \\ \rightarrow \frac{df(\boldsymbol{u}(\boldsymbol{x}))}{d\boldsymbol{x}} &= \left[ \begin{array}{ccc} \dfrac{\partial u_1}{\partial x_1} & \cdots & \dfrac{\partial u_n}{\partial x_1} \\ \vdots && \vdots \\ \dfrac{\partial u_1}{\partial x_m} & \cdots & \dfrac{\partial u_n}{\partial x_m} \\ \end{array} \right] \left[ \begin{array}{c} \dfrac{\partial f}{\partial u_1} \\ \vdots \\ \dfrac{\partial f}{\partial u_n} \end{array} \right] \\ &= \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_m} \end{array} \right] [u_1 \; \cdots \; u_n] \left[ \begin{array}{c} \dfrac{\partial}{\partial u_1} \\ \vdots \\ \dfrac{\partial}{\partial u_n} \end{array} \right] f(\boldsymbol{u}) \end{align*}$

積の微分

行列の積のスカラーによる微分

(18) $\begin{equation*} \frac{d\boldsymbol{(FG)}}{dx} = \frac{d\boldsymbol{F}}{dx}\boldsymbol{G} + \boldsymbol{F} \frac{d\boldsymbol{G}}{dx} \end{equation*}$

これは素直に次のように確認できる。

(19) $\begin{align*} \frac{d(\boldsymbol{FG})}{dx} &= \frac{d}{dx}\left[\sum_{j=1}^m f_{ij} g_{jk}\right] = \left[\sum_{j=1}^m \left(\frac{df_{ij}}{dx} g_{jk} + f_{ij} \frac{dg_{jk}}{dx} \right)\right] \\ &= \left[ \sum_{j=1}^m \frac{df_{ij}}{dx} g_{jk} \right] + \left[ \sum_{j=1}^m f_{ij} \frac{dg_{jk}}{dx} \right] \end{align*}$

一次～二次形式の微分

Axの形式

ベクトルAxをベクトルxで微分するのに(13)の考え方で計算する。

ベクトルxをn次、行列Aをm×nとすると、ベクトルAx次数はm次となる。微分する際に微分係数ベクトルはn×1の列ベクトル、Axは転置して1×mの行ベクトルとなり、結果はn×mの行列になる。その結果は元のAの転置行列となる。

(20) $\begin{equation*} \frac{d\left( (\boldsymbol{Ax})^T \right)}{d\boldsymbol{x}} = \boldsymbol{A}^T \end{equation*}$

(21) $\begin{equation*} \begin{align} & \frac{d}{d\boldsymbol{x}} \left[ \begin{array}{c} a_{11}x_1 + \cdots + a_{1j}x_j + \cdots + a_{1n}x_n \\ \vdots \\ a_{i1}x_1 + \cdots + a_{ij}x_j + \cdots + a_{in}x_n \\ \vdots \\ a_{m1}x_1 + \cdots + a_{mj}x_j + \cdots + a_{mn}x_n \\ \end{array} \right]^T \\ &= \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_j} \\ \vdots \\ \dfrac{\partial}{\partial x_n} \\ \end{array} \right] \left[ \begin{array}{c} a_{11}x_1 + \cdots + a_{1j}x_j + \cdots + a_{1n}x_n \\ \vdots \\ a_{i1}x_1 + \cdots + a_{ij}x_j + \cdots + a_{in}x_n \\ \vdots \\ a_{m1}x_1 + \cdots + a_{mj}x_j + \cdots + a_{mn}x_n \\ \end{array} \right]^T \\ &= \left[ \begin{array}{ccccc} a_{11} & \cdots & a_{i1} & \cdots & a_{m1} \\ \vdots && \vdots && \vdots \\ a_{1j} & \cdots & a_{ij} & \cdots & a_{mj} \\ \vdots && \vdots && \vdots \\ a_{1n} & \cdots & a_{in} & \cdots & a_{mn} \\ \end{array} \right] = \boldsymbol{A}^T \end{align} \end{equation*}$

x^2の形式

(22) $\begin{equation*} \frac{d(\boldsymbol{x}^T \boldsymbol{x})}{d\boldsymbol{x}} = 2 \boldsymbol{x} \end{equation*}$

［証明］

(23) $\begin{equation*} \left[ \begin{array}{c} \dfrac{\partial}{\partial x_1} \\ \vdots \\ \dfrac{\partial}{\partial x_n} \end{array} \right] [ x_1^2 + \cdots + x_n^2 ] = \left[ \begin{array}{c} 2x_1 \\ \vdots \\ 2x_n \end{array} \right] \end{equation*}$

x^TAxの形式

この場合、 $\boldsymbol{A}$ は正方行列で、 $\boldsymbol{x}$ と同じ次数でなければならない。

(24) $\begin{equation*} \frac{d}{d\boldsymbol{x}} \left(\boldsymbol{x}^T \boldsmbol{A} \boldsymbol{x} \right)= \left( \boldsymbol{A} + \boldsymbol{A}^T \right) \boldsymbol{x} \end{equation*}$

［証明］

(25) $\begin{align*} &\frac{d}{d \boldsymbol{x}} \left( [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{nn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] \right)\\ &=\frac{d}{d \boldsymbol{x}} \left( [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} a_{11} x_1 + \cdots + a_{1n} x_n \\ \vdots \\ a_{n1} x_1 + \cdots + a_{nn} x_n \end{array} \right] \right)\\ &= \frac{d}{d \boldsymbol{x}} \left( \left( a_{11} {x_1}^2 + \cdots + a_{1n} x_1 x_n \right) + \cdots + \left( a_{n1} x_n x_1 + \cdots + a_{nn} {x_n}^2 \right) \right) \end{array}\\ &=\left[ \begin{array}{c} \left( 2 a_{11} x_1 + \cdots + a_{1n} x_n \right) + a_{21} x_2 + \cdots + a_{n1} x_n \\ \vdots \\ a_{1n} x_1 + \cdots + a_{1n-1} x_{n-1} + \left( a_{n1} x_1 + \cdots + 2a_{nn} x_n \right) \end{array} \right] \\ &=\left[ \begin{array}{c} \left( a_{11} x_1 + \cdots + a_{1n} x_1 \right) + \left( a_{11} x_1 + \cdots + a_{n1} x_n \right) \\ \vdots \\ \left( a_{n1} x_1 + \cdots + a_{nn} x_n \right) + \left( a_{1n} x_1 + \cdots + a_{nn} x_n \right) \end{array} \right] \end{align*}$

転置行列

2020-04-18 / tau / コメントする

定義

(1) $\begin{equation*} {\boldsymbol{A}^T}_{ij} = {\boldsymbol{A}}_{ji} \end{equation*}$

性質

単独の行列

転置の転置

(2) $\begin{equation*} \left(\boldsymbol{A}^T\right)^T = \boldsymbol{A} \end{equation*}$

逆行列

(3) $\begin{equation*} \left( \boldsymbol{A}^T \right)^{-1} = \left( \boldsymbol{A}^{-1} \right)^T \end{equation*}$

［証明］

(4) $\begin{align*} &\boldsymbol{AA}^{-1} = \boldsymbol{I} \; \Leftrightarrow \; \left( \boldsymbol{AA}^_{-1} \right)^T = \boldsymbol{I}^T \; \Leftrightarrow \; \left( \boldsymbol{A}^{-1} \right)^T \boldsymbol{A}^T = \boldsymbol{I} \\ &\boldsymbol{A}^{-1} \boldsymbol{A} = \boldsymbol{I} \; \Leftrightarrow \quad \left( \boldsymbol{A}^{-1} \boldsymbol{A} \right)^T = \boldsymbol{I}^T \; \Leftrightarrow \; \boldsymbol{A}^T \left( \boldsymbol{A}^{-1} \right)^T = \boldsymbol{I} \end{align*}$

行列式

(5) $\begin{equation*} \left| \boldsymbol{A}^T \right| = \left| \boldsymbol{A} \right| \end{equation*}$

行列演算

線形性

(6) $\begin{equation*} (\alpha \boldsymbol{A})^T = \alpha \boldsymbol{A}^T \end{equation*}$

(7) $\begin{equation*} \left(\boldsymbol{A} + \boldsymbol{B}\right)^T = \boldsymbol{A}^T + \boldsymbol{B}^T \end{equation*}$

積

交換法則は成り立たない。

(8) $\begin{equation*} (\boldsymbol{AB})^T = \boldsymbol{B}^T \boldsymbol{A}^T \end{equation*}$

［証明］

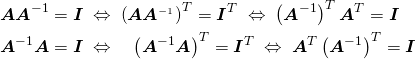
(9) $\begin{align*} \left( [ \boldsymbol{AB} ]_{ij} \right)^T = \left( \sum_k \boldsymbol{A}_{ik} \boldsymbol{B}_{kj} \right)^T = \sum_k \boldsymbol{B}_{jk} \boldsymbol{A}_{ki} =\boldsymbol{B}^T \boldsymbol{A}^T \end{align*}$

行列とベクトル

行列とベクトルの積

(10) $\begin{equation*} (\boldsymbol{Ax})^T = \boldsymbol{x}^T \boldsymbol{A}^T \end{equation*}$

すなわち

(11) $\begin{equation*} \left[ \begin{array}{ccc} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{m1} & \cdots & a_{mn} \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = [x_1 \; \cdots \; x_n] \left[ \begin{array}{ccc} a_{11} & \cdots & a_{m1} \\ \vdots & & \vdots \\ a_{1n} & \cdots & a_{mn} \\ \end{array} \right] \end{equation*}$

内積

(12) $\begin{equation*} \boldsymbol{x}^T \boldsymbol{x} = \langle \boldsymbol{x} , \boldsymbol{x} \rangle \end{equation*}$

すなわち

(13) $\begin{equation*} [x_1 \; \cdots \; x_n] \left[ \begin{array}{c} x_1 \\ \vdots \\ x_n \end{array} \right] = x_1^2 + \cdots + x_n^2 \end{equation*}$

waveデータセット – 線形回帰

2020-04-05 / tau / コメントする

O’Reillyの”Pythonではじめる機械学習”に載っている、scikit-learnの線形回帰のwaveデータセットへの適用の再現。

waveデータセットのサンプル数を60、train_test_split()でrandom_satet=42として、書籍と同じグラフを得る。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from mglearn.datasets import make_wave

xmin, xmax = -3, 3
ymin, ymax = -3, 3

X_source, y_source = make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X_source, y_source, random_state=42)

linreg = LinearRegression()
linreg.fit(X_train, y_train)

X_test = np.linspace(xmin, xmax, 2).reshape(-1, 1)
y_test = linreg.predict(X_test)

print(linreg.coef_[0], linreg.intercept_)

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(X_source, y_source, s=20)
ax.plot(X_test, y_test, c="tab:orange")

ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.grid()

ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from mglearn.datasets import make_wave

xmin, xmax = -3, 3

ymin, ymax = -3, 3

X_source, y_source = make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X_source, y_source, random_state=42)

linreg = LinearRegression()

linreg.fit(X_train, y_train)

X_test = np.linspace(xmin, xmax, 2).reshape(-1, 1)

y_test = linreg.predict(X_test)

print(linreg.coef_[0], linreg.intercept_)

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(X_source, y_source, s=20)

ax.plot(X_test, y_test, c="tab:orange")

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.grid()

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_aspect('equal')

plt.show()

また、訓練結果の係数、切片とスコアについても同じ結果を得ることができる。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from mglearn.datasets import make_wave

X, y = make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

linreg = LinearRegression()
linreg.fit(X_train, y_train)

print("coef_     : {}".format(linreg.coef_))
print("intercept_: {}".format(linreg.intercept_))

print("training score: {:.3f}".format(linreg.score(X_train, y_train)))
print("test score    : {:.3f}".format(linreg.score(X_test, y_test)))

# coef_     : [0.39390555]
# intercept_: -0.031804343026759746
# training score: 0.670
# test score    : 0.659

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from mglearn.datasets import make_wave

X, y = make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

linreg = LinearRegression()

linreg.fit(X_train, y_train)

print("coef_ : {}".format(linreg.coef_))

print("intercept_: {}".format(linreg.intercept_))

print("training score: {:.3f}".format(linreg.score(X_train, y_train)))

print("test score : {:.3f}".format(linreg.score(X_test, y_test)))

# coef_ : [0.39390555]

# intercept_: -0.031804343026759746

# training score: 0.670

# test score : 0.659

Breast cancer データセット – Logistic回帰による学習率曲線

2020-04-05 / tau / コメントする

概要

breast-cancerデータセットにscikit-learnのLogisticRegressionクラスでLogistic回帰を適用した結果。

手法全般の適用の流れはLogistic回帰～cancer～Pythonではじめる機械学習よりを参照。

ここではハイパーパラメーターを変化させたときの学習率の違いをみている。

学習率曲線

scikit-learnのLogisticRegressionクラスで、正則化のパラメーターを変化させたときの学習率曲線。同クラスにはsolver引数で収束計算のいくつかの手法が選択できるが、収束手法の違いによって意外に学習率曲線に違いが出た。またtrain_test_split()のrandom_stateを変えても違いがある。569のデータセットで訓練データとテストデータを分けてもいるが、その程度では結構ばらつきが出るということかもしれない。

まず、random_state=0とした場合の、4つの収束手法における学習率曲線を示す。L-BFGSは準ニュートン法の1つらしいので、Newton-CGと同じ傾向であるのは頷ける。SAG(Stochastic Average Gradient)はまた違った計算方法のようで、他の手法と随分挙動が異なる。収束回数はmax_iter=10000で設定していて、これくらいでも計算回数オーバーの警告がいくつか出る。回数をこれより2オーダー多くしても、状況はあまり変わらない。

random_state=11としてみると、liblinearでは大きく違わないが、他の3つの手法では傾向が違っていて、特にsagを用いた場合は訓練データの学習率の方がテストデータの学習率よりも低くなっている。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer

ds = load_breast_cancer()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X_train, X_test, y_train, y_test = \
    train_test_split(df, ds.target, stratify=ds.target, random_state=0)

C_sup = np.linspace(5, -4, 20)
C_val = 10**C_sup

solvers = ['liblinear', 'lbfgs', 'newton-cg', 'sag']


fig, axs = plt.subplots(2, 2, figsize=(8, 8))
axs_1d = axs.reshape(-1)

for ax, solver in zip(axs_1d, solvers):
    train_scores = np.empty(0)
    test_scores = np.empty(0)
    for C in C_val:
        logreg = LogisticRegression(C=C, solver=solver, max_iter=10000)
        logreg.fit(X_train, y_train)
        train_scores = np.append(train_scores, logreg.score(X_train, y_train))
        test_scores = np.append(test_scores, logreg.score(X_test, y_test))

    ax.plot(C_val, train_scores, label="Training scores")
    ax.plot(C_val, test_scores, label="Test scores")

    ax.set_xscale('log')
    ax.set_ylim(0.9, 1)
    ax.grid(True)
    ax.legend()
    ax.set_title(solver)

plt.show()

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

from sklearn.datasets import load_breast_cancer

ds = load_breast_cancer()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X_train, X_test, y_train, y_test = \

train_test_split(df, ds.target, stratify=ds.target, random_state=0)

C_sup = np.linspace(5, -4, 20)

C_val = 10**C_sup

solvers = ['liblinear', 'lbfgs', 'newton-cg', 'sag']

fig, axs = plt.subplots(2, 2, figsize=(8, 8))

axs_1d = axs.reshape(-1)

for ax, solver in zip(axs_1d, solvers):

train_scores = np.empty(0)

test_scores = np.empty(0)

for C in C_val:

logreg = LogisticRegression(C=C, solver=solver, max_iter=10000)

logreg.fit(X_train, y_train)

train_scores = np.append(train_scores, logreg.score(X_train, y_train))

test_scores = np.append(test_scores, logreg.score(X_test, y_test))

ax.plot(C_val, train_scores, label="Training scores")

ax.plot(C_val, test_scores, label="Test scores")

ax.set_xscale('log')

ax.set_ylim(0.9, 1)

ax.grid(True)

ax.legend()

ax.set_title(solver)

plt.show()

ndarray.reshape – 配列の形状変更

2020-04-05 / tau / コメントする

基本

配列の形状変更は、reshape()メソッドで行う。reshape()メソッドは、元の配列を破壊せず新たな配列を生成する。

具体のいろいろな使い方は、ndarray.reshapeの使い方を参照

以下の例では6個の要素の1次元配列を2×3の2次元配列に変更し、それをさらに3 ×2の2次元配列に変更している。要素は常に行を上から、各行の列要素を左からネストした形で埋めていく。

import numpy as np

a = np.arange(6)
b = a.reshape(2, 3)
c = b.reshape(3, 2)
print(a)
print(b)
print(c)

# [0 1 2 3 4 5]
# [[0 1 2]
#  [3 4 5]]
# [[0 1]
#  [2 3]
#  [4 5]]

import numpy as np

a = np.arange(6)

b = a.reshape(2, 3)

c = b.reshape(3, 2)

print(a)

print(b)

print(c)

# [0 1 2 3 4 5]

# [[0 1 2]

# [3 4 5]]

# [[0 1]

# [2 3]

# [4 5]]

暗黙指定

サイズ変更の際、ある次元の要素数を-1とすると、他の要素数に合わせて適切に設定してくれる。

以下の例では2×3×2の3次元配列をつくり、それを3×2×2に変形しているが、2次元目を-1として1次元目と3次元目から設定させている。

import numpy as np

a1 = np.arange(10, 16).reshape(3, 2)
a2 = np.arange(20, 26).reshape(3, 2)
b = np.array([a1, a2])
print(b.ndim, b.shape)
print(b)

c = b.reshape(3, -1, 2)
print(c)

# 3 (2, 3, 2)
# [[[10 11]
#   [12 13]
#   [14 15]]
# 
#  [[20 21]
#   [22 23]
#   [24 25]]]
# [[[10 11]
#   [12 13]]
# 
#  [[14 15]
#   [20 21]]
# 
#  [[22 23]
#   [24 25]]]

import numpy as np

a1 = np.arange(10, 16).reshape(3, 2)

a2 = np.arange(20, 26).reshape(3, 2)

b = np.array([a1, a2])

print(b.ndim, b.shape)

print(b)

c = b.reshape(3, -1, 2)

print(c)

# 3 (2, 3, 2)

# [[[10 11]

# [12 13]

# [14 15]]

# [[20 21]

# [22 23]

# [24 25]]]

# [[[10 11]

# [12 13]]

# [[14 15]

# [20 21]]

# [[22 23]

# [24 25]]]

この方法は、たとえば行ベクトルの配列を列ベクトルに変換するときに使われる。以下の例では1次元の配列をつくり、それを列ベクトルとするのに、列数を1で固定し、行数を-1として算出させている。

import numpy as np

a = np.arange(3)
b = a.reshape(-1, 1)
print(b)

# [[0]
#  [1]
#  [2]]

import numpy as np

a = np.arange(3)

b = a.reshape(-1, 1)

print(b)

# [[0]

# [1]

# [2]]

1次元化するときの注意

多次元配列や列ベクトルを1次元化するとき、行数を1、列数を-1で暗黙指定すると求める1次元配列を1つだけ含む2次元の配列になる。こうなってしまのはreshape()の引数で1行×n列の2次元で指定したため。

import numpy as np

a = np.arange(12).reshape(2, 3, 2)
print(a)
print(a.reshape(1, -1))

# [[[ 0  1]
#   [ 2  3]
#   [ 4  5]]
# 
#  [[ 6  7]
#   [ 8  9]
#   [10 11]]]
# [[ 0  1  2  3  4  5  6  7  8  9 10 11]]

b = np.arange(3).reshape(-1, 1)
print(b)
print(b.reshape(1, -1))

# [[0]
#  [1]
#  [2]]
# [[0 1 2]]

import numpy as np

a = np.arange(12).reshape(2, 3, 2)

print(a)

print(a.reshape(1, -1))

# [[[ 0 1]

# [ 2 3]

# [ 4 5]]

# [[ 6 7]

# [ 8 9]

# [10 11]]]

# [[ 0 1 2 3 4 5 6 7 8 9 10 11]]

b = np.arange(3).reshape(-1, 1)

print(b)

print(b.reshape(1, -1))

# [[0]

# [1]

# [2]]

# [[0 1 2]]

そこで、size属性で1つの整数だけを指定すると、1次元でその要素数の配列になってくれる。

import numpy as np

a = np.arange(12).reshape(2, 3, 2)
print(a.reshape(a.size))

b = np.arange(3).reshape(-1, 1)
print(b.reshape(b.size))

# [ 0  1  2  3  4  5  6  7  8  9 10 11]
# [0 1 2]

import numpy as np

a = np.arange(12).reshape(2, 3, 2)

print(a.reshape(a.size))

b = np.arange(3).reshape(-1, 1)

print(b.reshape(b.size))

# [ 0 1 2 3 4 5 6 7 8 9 10 11]

# [0 1 2]

さらには、引数を-1のみで指定すると、配列のサイズを適当に持ってきて適用してくれる。

import numpy as np

a = np.arange(12).reshape(2, 3, 2)
print(a.reshape(-1))

b = np.arange(3).reshape(-1, 1)
print(b.reshape(-1))

# [ 0  1  2  3  4  5  6  7  8  9 10 11]
# [0 1 2]

import numpy as np

a = np.arange(12).reshape(2, 3, 2)

print(a.reshape(-1))

b = np.arange(3).reshape(-1, 1)

print(b.reshape(-1))

# [ 0 1 2 3 4 5 6 7 8 9 10 11]

# [0 1 2]

これは列ベクトルを行ベクトル化するときのほか、pyplotで複数のAxesインスタンスを行×列の形で受け取った時に、全てのインスタンスに同じ設定を適用したいときなどに1次元化してループで回す、といったようなことにも使える。

ndarray – 配列の次元・形状・サイズ

2020-04-05 / tau / コメントする

`ndim`属性～配列の次元

ndim属性は配列の次元を整数で返す。

1次元配列を1つだけ要素に持つ配列や列ベクトルの次元が2となっている点に注意。とにかく[]のネストの数だと考えればよい。

import numpy as np

a = np.array([1, 2, 3])
print(a.ndim)  # 1

b = np.array([
    [1, 2, 3],
    [4, 5, 6]
])
print(b.ndim)  # 2

c = np.array([
    [[1, 2], [3, 4]],
    [[5, 6], [7, 8]]
])
print(c.ndim)  # 3

d = np.array([[1, 2, 3]])
print(d.ndim)  # 2

e = np.array([
    [1],
    [2],
    [3],
])
print(e.ndim)  # 2

import numpy as np

a = np.array([1, 2, 3])

print(a.ndim) # 1

b = np.array([

[1, 2, 3],

[4, 5, 6]

])

print(b.ndim) # 2

c = np.array([

[[1, 2], [3, 4]],

[[5, 6], [7, 8]]

])

print(c.ndim) # 3

d = np.array([[1, 2, 3]])

print(d.ndim) # 2

e = np.array([

[1],

[2],

[3],

])

print(e.ndim) # 2

`shape`属性～配列の形状

shape属性は配列の形状を返す。

1次元1行の単純な配列のときにはshapeが(1, n)とならないのが気になるがこれは結果が常にタプルで返されるためで、1次元とわかっているときには1つの整数が返ってくると考えてよい。

ndim=2となる形状の場合にはタプルも2要素となって、shape=(行数, 列数)となる。より多次元の場合、外側の次元の要素数からの順番になる。

import numpy as np

a = np.array([1, 2, 3])
print(a.shape)  # (3,)

b = np.array([
    [1, 2, 3],
    [4, 5, 6]
])
print(b.shape)  # (2, 3)

c = np.array([
    [[11, 12, 13, 14],
     [15, 16, 17, 18],
     [19, 20, 21, 22]],
    [[51, 52, 53, 54],
     [55, 56, 57, 58],
     [59, 60, 61, 62]]
])
print(c.shape)  # (2, 3, 4)

d = np.array([[1, 2, 3]])
print(d.shape)  # (1, 3)

e = np.array([
    [1],
    [2],
    [3],
])
print(e.shape)  # (3, 1)

import numpy as np

a = np.array([1, 2, 3])

print(a.shape) # (3,)

b = np.array([

[1, 2, 3],

[4, 5, 6]

])

print(b.shape) # (2, 3)

c = np.array([

[[11, 12, 13, 14],

[15, 16, 17, 18],

[19, 20, 21, 22]],

[[51, 52, 53, 54],

[55, 56, 57, 58],

[59, 60, 61, 62]]

])

print(c.shape) # (2, 3, 4)

d = np.array([[1, 2, 3]])

print(d.shape) # (1, 3)

e = np.array([

[1],

[2],

[3],

])

print(e.shape) # (3, 1)

`size`属性～配列のサイズ

size属性で得られる配列のサイズは配列の要素数。

import numpy as np

a = np.array([1, 2, 3])
print(a.size)  # 3

b = np.array([
    [1, 2, 3],
    [4, 5, 6]
])
print(b.size)  # 6

c = np.array([
    [[1, 2], [3, 4]],
    [[5, 6], [7, 8]]
])
print(c.size)  # 8

d = np.array([[1, 2, 3]])
print(d.size)  # 3

e = np.array([
    [1],
    [2],
    [3],
])
print(e.size)  # 3

import numpy as np

a = np.array([1, 2, 3])

print(a.size) # 3

b = np.array([

[1, 2, 3],

[4, 5, 6]

])

print(b.size) # 6

c = np.array([

[[1, 2], [3, 4]],

[[5, 6], [7, 8]]

])

print(c.size) # 8

d = np.array([[1, 2, 3]])

print(d.size) # 3

e = np.array([

[1],

[2],

[3],

])

print(e.size) # 3

概要

各種図形

定義

定式化

行列による表示

定義式

計算例

次数2の場合

次数3の場合

記号の定義

ベクトル・行列をスカラーで微分

スカラーをベクトルで微分

スカラーを行列で微分

ベクトルをベクトルで微分

公式

一般形

単位行列

合成関数

積の微分

行列の積のスカラーによる微分

一次～二次形式の微分

Axの形式

x^2の形式

xTAxの形式

定義

性質

単独の行列

転置の転置

逆行列

行列式

行列演算

線形性

積

行列とベクトル

行列とベクトルの積

内積

概要

学習率曲線

基本

暗黙指定

1次元化するときの注意

ndim属性～配列の次元

shape属性～配列の形状

size属性～配列のサイズ

x^TAxの形式

`ndim`属性～配列の次元

`shape`属性～配列の形状

`size`属性～配列のサイズ