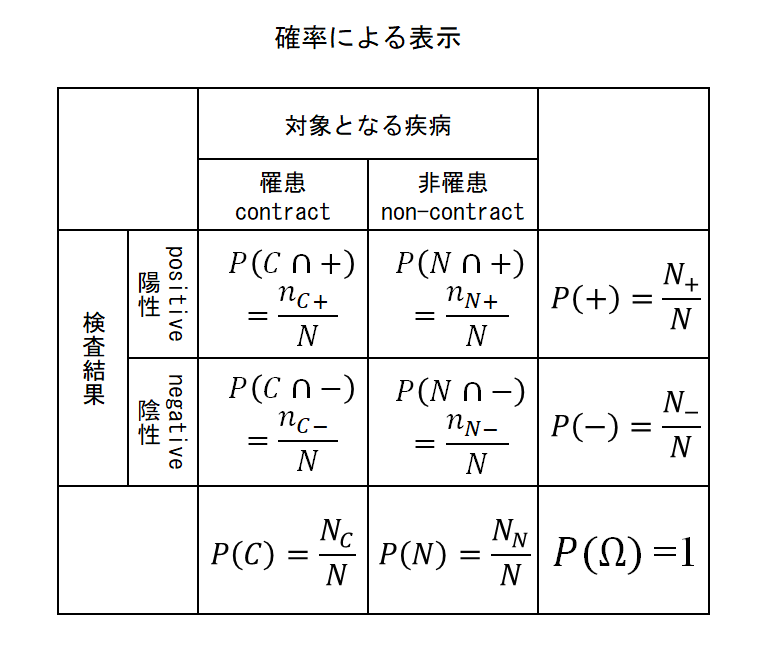
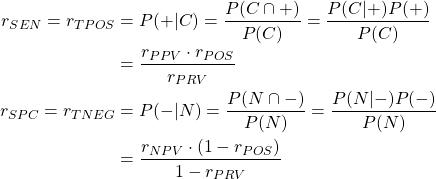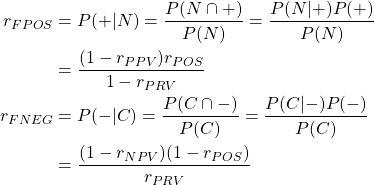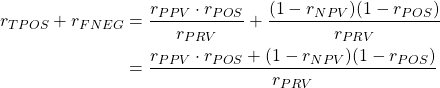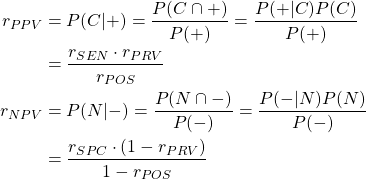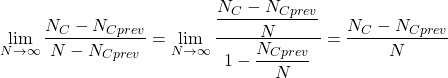Ruby – 基本的なリテラル

2020-09-20 / tau / コメントする

数値

整数

puts 123, -123

# 123
# -123

puts 123, -123

# 123

# -123

基数を指定する場合。

puts 0d255
puts 0b11111111
puts 0o377, 0377

# 255
# 255
# 255
# 255

puts 0d255

puts 0b11111111

puts 0o377, 0377

# 255

先頭がゼロの場合は8進数と解釈される点に注意。8進数と解釈できない場合はエラーになる。

puts 010
puts 08 -> Invalid octal digit

# 8

puts 010

puts 08 -> Invalid octal digit

# 8

実数

puts 123.456   # 固定小数点
puts 1.23456e2 # 浮動小数点

# 123.456
# 123.456

puts 123.456 # 固定小数点

puts 1.23456e2 # 浮動小数点

# 123.456

小数点以下をゼロとすると実数のリテラルになるが、小数点のみを付けるとエラーになる。

puts 123.0
puts 123. -> NoMethodError

# 123.0

puts 123.0

puts 123. -> NoMethodError

# 123.0

0～1の小数点では、先頭のゼロは省略できない。

puts 0.123
puts .123  -> syntax error

# 0.123

puts 0.123

puts .123 -> syntax error

# 0.123

有理数

末尾に'r'を付けると有理数となり、分数形式で保持される。

puts 1.25r
puts 1.414r

# 5/4
# 707/500

puts 1.25r

puts 1.414r

# 5/4

# 707/500

複素数

'i'の直前に数値を並べると虚数となり、複素数形式で保存される。

puts 1 + 2.1i
puts 1i * 1i

# 1+2.1i
# -1+0i

puts 1 + 2.1i

puts 1i * 1i

# 1+2.1i

# -1+0i

文字列

ダブルクォートかシングルクォートで囲む。

puts "Ruby string"
puts 'Ruby string'

# Ruby string
# Ruby string

puts "Ruby string"

puts 'Ruby string'

# Ruby string

ダブルクォートで囲むとバックスラッシュ記法は特殊文字として解釈されるが、シングルクォートで囲むとバックスラッシュが単なる文字として扱われる。

puts "Ruby\nstring"
puts 'Ruby\nstring'

# Ruby
# string
# Ruby\nstring

puts "Ruby\nstring"

puts 'Ruby\nstring'

# Ruby

# string

# Ruby\nstring

空白をはさんで並んだ文字列は結合される。

puts "Ruby" "String"

# RubyString

puts "Ruby" "String"

# RubyString

文字リテラル

'?'に続く一文字は文字列として扱われる。

puts ?字
puts ?\u5b57

# 字
# 字

puts ?字

puts ?\u5b57

# 字

ヒアドキュメント

'<<[識別子]'の次の行から'[識別子]'の直前の行までが複数行にわたる文字列として解釈される。

puts <<EOS
1行目
2行目
EOS

# 1行目
# 2行目

puts <<EOS

1行目

2行目

EOS

# 1行目

# 2行目

論理値

論理値のリテラルとしてtrue、falseが定義されている。

puts true ? "True" : "False"
puts false ? "True" : "False"

# True
# False

puts true ? "True" : "False"

puts false ? "True" : "False"

# True

# False

PCR検査と条件付確率

2020-09-17 / tau / コメントする

概要

2020年9月時点で、COVID-19いわゆる新型コロナウイルス感染症は収束を見ていない。このコロナウイルスについて、PCR検査を増やすべきだ、いや効果はない／医療現場の負担が増えるだけ、といろいろな論が飛び交っている。

不思議なことに、多くの人の目に触れるマスメディアや一般的なネットのソースでは、殆どの場合定性的な、あるいはそれ以前の論拠もないようなものばかりが並んでいる。意図してネットで検索すると確率論を適用しているものも見られるが、残念ながらほとんどの人はこれらのコンテンツはその意義や存在さえ意識しないだろう。

新型コロナウイルスの場合、計算に必要なデータは未詳のようだが、少なくともベイズ理論を適用する教科書的なパターンの問題である。そこで、この機に学んだいくつかの用語や概念、計算過程などをまとめておく。

なお、難病検査を例にした条件付確率の考え方はこちらにまとめている。

基本のデータ

定義

鍵となる指標の定義を確認するとともに、その記号を以下のように定義する。

医学・疫学上の指標

陽性率／陰性率

以下は罹患している／罹患していないことがわかっている人の集合に対する割合。

感度(sensitivity)：r_SEN
真陽性率(true positive rate)：r_TPOS: 罹患している人の検査結果が陽性と判定される割合。
特異度(specificity)：r_SPC
真陰性率(true negative rate)：r_TNEG: 罹患していない人の検査結果が陰性と判定される割合。
偽陽性率(false positive rate)：r_FPOS: 罹患していない人の検査結果が陽性と判定される割合。
偽陰性率(false negative rate)：r_FNEG: 罹患している人の検査結果が陰性と判定される割合。

これらの関係を図にすると以下の通り。真／偽の陽性率／陰性率は罹患者数のみあるいは非罹患者数のみの集団に対して、検査の判定結果を集計して計算される。表から、検査判定の陽性／陰性の割合は問題にしていないことがわかる。

的中率

次に検査結果が判明している集団の実際の罹患状態に関する割合。

陽性的中率(Positive Predictive Value: PPV, PV+)：r_P_PV: 検査で陽性と判定された人のうち、実際に罹患者である割合。
陰性的中率(Negative Predictive Value: NPV, PV-)：r_NPV: 検査で非陽性と判定された人のうち、実際に罹患していない者である割合。

これらは検査の判定結果が陽性あるいは陰性の集団における罹患／非罹患の人の割合で、罹患している（あるいはしていない）人の全体の割合は問題にしていない。

有病率／陽性率など

以下は対象となる集団全体における検査結果の割合や罹患状態の割合。

陽性率(positive rate)：r_pos: 検査で陽性と判定された人の割合。

有病率(Prevalence / Prevalence rate)：r_PRV: ある時点における疾病者数の人口に対する割合。
罹患率(Incidence / Incidence rate)：r_INC: ある期間において、疾病リスクのある人が対象とする疾病に罹患する割合。

これらは対象エリアの全員に対して罹患している人の割合、検査結果が陽性の人の割合である。有病率と罹患率の違いは一般にはあまり伝えられていないようだ。図にすると以下のようになる。

補足：感度と特異度について

「感度(sensitivity)」が「罹患している」という帰無仮説が真なのに検査で陰性と判定してしまう誤り、いわば「第一種の過誤」を起こさない確率と言える。

また「特異度(specificity)」が「罹患していない」という仮説（上の帰無仮説の対立仮説）が真なのに検査で陽性と判定してしまう誤り、すなわち「第二種の過誤」を起こさない確率と言える。

補足：「特異度」という表現について

「特異度」の用語には違和感がある。日本語の「特異な」ならsinglularやpeculiarの方が近く、specificは「明確な」、「特定の」というのが相当する（specifyという動詞もその意味でつかわれる）。「特別な」というニュアンスもあるようだが、「特異」というのは言い過ぎではないか。

specificityは罹患していない人を検査で陰性と正しく判定する割合なので、罹患していない人が大勢だとすると、その明白な事実を支持する割合、「明白度」とすると、ちょっと意味が分からなくなる。あるいは、その人が罹患していないということを特定するなら、せめて「特定度」くらいか。

いずれにしても、「特異度」という表現が使われているのは、英語の単語のニュアンスからしても、そもそもの意味合いからしても気持ちが悪い。

ここで定義する記号

C / N: 罹患している(contract)／罹患していない(non-contract)の人の集合
+ / −: 検査結果が陽性／陰性の人の集合
N: 検査人口
N₊ / N₋: それぞれ検査結果が陽性／陰性の人口
N_C / N_N: 検査を受けた人のうち、それぞれ罹患している(contract)／罹患していない(non-contract)人の人口
n_C₊ / n_C_– , n_N₊ / n_N_–: 検査を受けた人のうち、それぞれ、罹患していてかつ検査結果が陽性(C+)あるいは陰性(C−)、罹患しておらずかつ検査結果が陽性(N+)あるいは陰性(N−)の人の人口

これらを表で整理すると以下の通り。

また、これらから計算される確率は以下の通り。

条件付確率による表示

感度／特異度（真陽性率／真陰性率）

感度や特異度は、ある人が罹患している／罹患していない場合に検査結果が陽性／陰性となる確率ともいえる。これを条件付確率で表示し、的中率による表現に変換すると以下のようになる。

(1) $\begin{align*} r_{SEN} = r_{TPOS} &= P(+|C) = \frac{P(C \cap +)}{P(C)} =\frac{P(C|+)P(+)}{P(C)} \\ &= \frac{r_{PPV} \cdot r_{POS}}{r_{PRV}}\\ r_{SPC} = r_{TNEG} &= P(-|N) = \frac{P(N \cap -)}{P(N)} = \frac{P(N|-)P(-)}{P(N)} \\ &= \frac{r_{NPV} \cdot (1 - r_{POS})}{1 - r_{PRV}} \end{align*}$

偽陽性率／偽陰性率

偽陽性／偽陰性についても条件付確率で表し、これらを的中率による表現に変換すると以下のようになる。

(2) $\begin{align*} r_{FPOS} &= P(+|N) = \frac{P(N \cap +)}{P(N)} = \frac{P(N|+) P(+)}{P(N)}\\ &= \frac{(1 - r_{PPV}) r_{POS}}{1 - r_{PRV}} \\ r_{FNEG} &= P(-|C) = \frac{P(C \cap -)}{P(C)} = \frac{P(C|-) P(-)}{P(C)} \\ &= \frac{(1 - r_{NPV}) (1 - r_{POS})}{r_{PRV}} \end{align*}$

たとえばここで真陽性率と偽陰性率を加えると、

(3) $\begin{align*} r_{TPOS} + r_{FNEG} &= \frac{r_{PPV} \cdot r_{POS}}{r_{PRV}} + \frac{(1 - r_{NPV}) (1 - r_{POS})}{r_{PRV}} \\ &= \frac{r_{PPV} \cdot r_{POS} + (1 - r_{NPV}) (1 - r_{POS})}{r_{PRV}} \end{align*}$

ここで総数Nを仮定して分母分子にかければ、結果は1となることがわかる。

陽性的中率／陰性的中率

的中率は検査の判定陽性／陰性に対して、その対象者が実際に罹患／非罹患である割合を表す。これを条件付確率で表して陽性率や陰性率で表すと以下のようになる。

(4) $\begin{align*} r_{PPV} &= P(C|+) = \frac{P(C \cap +)}{P(+)} =\frac{P(+|C)P(C)}{P(+)}\\ &= \frac{r_{SEN} \cdot r_{PRV}}{r_{POS}} \\ r_{NPV} &= P(N|-) = \frac{P(N \cap -)}{P(-)} = \frac{P(-|N)P(N)}{P(-)} \\ &= \frac{r_{SPC} \cdot (1 - r_{PRV})}{1 - r_{POS}} \end{align*}$

実際の使われ方

多くの場合、検査方法の精度を確認するには、「罹患している人と罹患していない人を連れてきて検査をしてみる」というのが妥当だろう。感染症などで疑いがある人が医療機関に集まるから、そういうところで臨床的に試すのだろう。場合によって臨床例が少ない場合は、とにかく検査方法を適用しながら、実際の罹患状態をトレースするという方法がとられるのかもしれないが。

ただCOVID-19のPCR検査の場合、データが公表されていないのかどうかわからないが、感度については適当に（あるいは他サイトで使われている値を持ってきて）設定したりしているものしか見当たらない。以下のような手順が見られる。

感度と特異度を適当に設定する。感度は70%、特異度は99%というのがほとんど。
対象エリアの陽性者数nと総人口Nを持ってくる。
陽性者数を感度で割って、罹患者数を算出。
罹患者数を総人口で割って有病率を算出。
総人口から有病人口を引いて非罹患者数を算出。
非罹患者数と特異度の定義から偽陽性者数を算出。
以上のパラメーターを使って陽性的中率を算出。

計算された陽性的中率がかなり低いと主張しているものや、オーソリティーがありそうなサイトでも例題みたいな数字を示して有病率10%くらいで設定したりしているものや、結構混乱しているようだ。

ここで陽性的中率を感度で微分して、感度を見てみる（ややこしい）。

(5) $\begin{align*} \frac{d r_{PPV}}{d r_{SEN}} = \frac{r_{PRV}}{r_{POS}} \\ \end{align*}$

有病率が10000人に一人、陽性判定率が100人にひとりくらいなら、1%くらいで、感度（真陽性率）が数十%くらい違っても差は出なさそうだ。それよりも有病率がかなり低いと、いくら高感度の検査方法でも陽性的中率がかなり低くなりそうなことが式から読み取れる。

一方偽陽性率の方は、有病率や陽性的中率が結構低いとすると、陽性判定率の値が効いてくる。これは結構無視できないレベルのように思えるが。

ただ、共通して使えるデータが見当たらないので、数値の信憑性が揺らいでいるように思える。罹患・非罹患を計算するのに母数にエリアの全人口を使ったりするのは、検査をしていない人すべてを非罹患とみているので有病率を過少に見積もることになるだろう。

退院前の検査を含むかどうかなど定義の問題はあるが、そのようなフラグを立てたデータを集約するだけでも有益な情報になると思う。

罹患率と有病率

2020-09-14 / tau / コメントする

概要

2020年、COVID-19（新型コロナウイルス）の感染は続き、PCR検査が毎日のように各都道府県で行われている。これに伴って検査の信頼性がときどき話題になることがある（もっと真面目に議論されてもいいと思うが）。偽陽性／偽陰性などについて、一度Bayes理論などによって自分でトレースしてみようとしたときに、有病率と罹患率の違いがあることがわかってきたので、一度まとめてみる。

有病率

有病率を簡単に言うと、ある時点において、人口に対して疾病にかかっている人の割合、ということになる。Prevalence rateまたは単にPrevelanceと呼ばれることも多い。

より正確には、有病率r_Pは以下のように定義される。

(1) $\begin{equation*} r_P = \frac{N_C}{N_R}} \end{equation*}$

ここでN_Cはある時点における疾病者数(C: Contract)、N_Rは当該疾病のリスクを有する母集団の人数(R: Risk)。

とはいっても、当該疾病リスクを有する人を除外することはなかなか難しいので、対象とするエリアの人口を近似値として用いるのが一般的らしい。

また、ある時期と言っても疾病者数や人口の調査にはそれなりの時間がかかるため、ある期間に調査した結果を「いついつ時点」としたその時点で扱われるだろう。

有病率は0～1の実数だが、通常は対人口千人あたりとか10万人あたりで示されることが多いとのことである。

ここでPrevalenceという言葉は、流行するとか行き渡るといった意味であり、ある疾病がある時点でどれだけ広がっているか、というイメージになるだろう。

罹患率／発生率

罹患率を簡単に言うと、ある期間において対象とする疾病リスクを有する者が罹患する割合、ということになる。有病率はIncidence rateまたは単にIncidenceと言われることが多い。本来の意味で言うと「発生率」の方がより妥当で、実際にその用語も使われている。ちなみにincidentは出来事、incidenceは(望ましくない事象の)発生率・頻度という意味。

より正確には、罹患率r_Iは以下のように定義される。

(2) $\begin{equation*} r_I = \frac{N_I}{N_R}} \end{equation*}$

ここでN_Iはある期間内に新たに罹患した人の数(I: Incidence)、N_Rは観察期間内に当該疾病のリスクを有する集団の延べ人数(R: Risk)。

分子の方は新たに罹患した人の数なので、観察期間より前から罹患している人は含まれない。

有病率と罹患率（発生率）

有病率はある時点tにおける罹患者の数を表し、罹患率はある期間Δtにおける新たな罹患者数を表す。いわば有病率は罹患者の関数値、罹患率は罹患者数の変化率のうち発生による増加率を表すことになる（時間で除していないので罹患が広がるスピードの概念は含まれていない）。

また、罹患率以外に疾病が治癒する人、疾病により死亡する人、観察エリア外に出て行ってしまう人はいずれも負の変化率に相当するが、これらを含めた（あるいはこれらを総括した「罹患減少率」のような）パラメーターはあまり登場しない。

したがって、この2つのデータだけを見ていると、罹患者数が増大しているのに有病率が変化しなかったり減少する場合がある。

なお、有病率にしても罹患率にしても一定の期間で捕捉しなければならないが、一つ違う点は、対象となる期間より前から罹患していた人は罹患率の場合分母・分子の両方から除かれるという点である。一般に中止するエリアの人口に比べてそのような人の数は少ないので、近似的には既罹患者の分だけ率が小さくなる。

(3) $\begin{align*} \lim_{N \rightarrow \infty} \frac{N_C - N_{Cprev}}{N - N_{Cprev}} = \lim_{N \rightarrow \infty} \frac{\dfrac{N_C - N_{Cprev}}{N}}{1 - \dfrac{N_{Cprev}}{N}} = \frac{N_C - N_{Cprev}}{N} \end{align*}$

どういうときにどちらを使うか

以上の点を踏まえると、有病率と罹患率はそれぞれ次のような場合に有用と思われる。

有病率

その時点時点での、疾病への対策を検討する場合。たとえば、

疾病に対する薬品を準備するのにどの程度の総量が必要か検討する場合
地域や国などの対策重点度を判断する場合

罹患率

疾病の発生状況を重視する場合。たとえば、

感染症などの拡大期に、その危険性を判断する場合の一つの指標として
- ここで「一つの指標」としたのは、その他に有病期間、致死率など「単に罹っただけ」で騒ぐのではない判断要素も必要と考えたため。
疾病に対する予防法の効果を検証する場合

PCR検査？

2020年9月時点、COVID-19（新型コロナウイルス）の発症は続いており、PCR検査に関する議論も喧しい。個別の陽性反応に対してどのように対処するかという議論と別に、そもそもPCR検査の偽陽性／偽陰性、陽性／陰性的中率を議論するときは、有病率と罹患率のどちらを使うのが適切だろうか。

まず罹患率の方を考えてみる。

各都道府県でPCR検査が毎日行われているが、陽性率とのセットで考えるなら、PCR検査の結果もリアルタイムに近い形で（少なくともそういう思想で）発生者の全容を捉えるべきだろう。ところがその数は日単位で悉皆の調査というレベルには程遠い（日本に限らずこれはどこの国もそうだ）。一か月程度で各都道府県の全人口の検査ができるなら月単位での罹患者増加状況は捉えられるが、それでも実現性には難があり、スピードが遅すぎる。まして一週間単位で（しかも毎週？）そのようなことをしようとするのも無理だ。したがって、PCR検査に対して罹患率の考えを適用するのは難しいだろう。考えてみれば、罹患率の場合は既発生者が除かれるのだから、ヒアリングか何かで期間前に罹患していた人を除外しなければ分母と分子で意味が違ってしまう。

となると、PCR検査でいろいろとデータをいじるのは、有病率を使って、ということになる。

「期間前の既発生者も除かない」ということと、検査で陽性／陰性になった人の状況からその時点での全容を推測する、という点から見れば、Bayes理論で条件付確率を計算するときなどに用いるのは有病率だろう。

まとめ

罹患率と有病率の区別は、医学・疫学の世界ではあたりまえとされていることが、あまり伝わっていない例の一つだ。違いを説明しようとするとやっかいだが、そういうことを明快に伝えて、受け取る側も腹に落とすことができれば一番いいのだが。

これはIT業界、建設業界でも同じで、説明に関する意識の問題（その前段の必要性を感じるかどうかの問題）であるとともに、門外の専門家や一般の多くの人の側が理解しようとする文化も大切かもしれない。技術・政策や危機管理に関するコミュニケーションの問題（発する側、受ける側のどちらも）に通ずると思う。

scikit-learn – predict_proba

2020-09-09 / tau / コメントする

概要

decision_function()は各データが推測したクラスに属する確信度(confidence)を表すが、超平面のパラメータに依存し、そのレンジや値の大きさと確信度の関係が明確ではない。

これに対してpredict_probaは、それぞれのターゲットが予測されたクラスに属する確率を0～1の実数で表す。2クラス分類では、結果の配列の形状は(n_sumples, 2)となる。

`predict_proba()`の挙動

以下はmake_circles()で生成した2クラスのデータをGradient Boostingによって分類したときの確信度。各データに対応した2要素の配列の1つ目がクラス0(blue)、2つ目がクラス1(orange)に属する確率を表し、2つの和は1となる。なお16行目でsuppress=Trueとすることで、ndarrayの表示を常に固定小数点としている。

import numpy as np
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)
y_named = np.array(["blue", "orange"])[y]

X_train, X_test, y_train, y_test, y_train_named, y_test_named = \
    train_test_split(X, y, y_named, random_state=0)

gbc = GradientBoostingClassifier(random_state=0)
gbc.fit(X_train, y_train_named)

pred_prob = gbc.predict_proba(X_test)
np.set_printoptions(suppress=True)
print(pred_prob)

# [[0.01573626 0.98426374]
#  [0.84575653 0.15424347]
#  [0.98112869 0.01887131]
#  .....
#  [0.06307595 0.93692405]
#  [0.93442475 0.06557525]
#  [0.86619957 0.13380043]]

import numpy as np

from sklearn.ensemble import GradientBoostingClassifier

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

y_named = np.array(["blue", "orange"])[y]

X_train, X_test, y_train, y_test, y_train_named, y_test_named = \

train_test_split(X, y, y_named, random_state=0)

gbc = GradientBoostingClassifier(random_state=0)

gbc.fit(X_train, y_train_named)

pred_prob = gbc.predict_proba(X_test)

np.set_printoptions(suppress=True)

print(pred_prob)

# [[0.01573626 0.98426374]

# [0.84575653 0.15424347]

# [0.98112869 0.01887131]

# .....

# [0.06307595 0.93692405]

# [0.93442475 0.06557525]

# [0.86619957 0.13380043]]

`decision_function()`との比較

先のコードに以下を続けて、predict_proba()による確率、予測されたクラス、decsion_function()の値と、各データの正解クラスを並べて表示する。予測されたクラスの方の確率が大きいこと、その予測結果とdecision_function()の符号が一致していることが確認できる。

prob0 = pred_prob[:, 0]
prob1 = pred_prob[:, 1]

data = DataFrame()
data["prob0"] = prob0
data["prob1"] = prob1
data["pred"] = gbc.predict(X_test)
data["dec_func"] = gbc.decision_function(X_test)
data["correct"] = y_test_named
print(data)

#        prob0     prob1    pred  dec_func correct
# 0   0.015736  0.984264  orange  4.135926  orange
# 1   0.845757  0.154243    blue -1.701699    blue
# 2   0.981129  0.018871    blue -3.951061    blue
# .....
# 22  0.063076  0.936924  orange  2.698263  orange
# 23  0.934425  0.065575    blue -2.656733    blue
# 24  0.866200  0.133800    blue -1.867766    blue

prob0 = pred_prob[:, 0]

prob1 = pred_prob[:, 1]

data = DataFrame()

data["prob0"] = prob0

data["prob1"] = prob1

data["pred"] = gbc.predict(X_test)

data["dec_func"] = gbc.decision_function(X_test)

data["correct"] = y_test_named

print(data)

# prob0 prob1 pred dec_func correct

# 0 0.015736 0.984264 orange 4.135926 orange

# 1 0.845757 0.154243 blue -1.701699 blue

# 2 0.981129 0.018871 blue -3.951061 blue

# .....

# 22 0.063076 0.936924 orange 2.698263 orange

# 23 0.934425 0.065575 blue -2.656733 blue

# 24 0.866200 0.133800 blue -1.867766 blue

このデータをクラス0(blue)に対する確率(prob0)でソートし、decision_function()との関係を見てみると、以下のことがわかる。

blueクラスの確率が高いとdecision_functionの確信度はマイナスで絶対値が大きくなり、orangeクラスの確率が高いと確信度はプラスで絶対値が大きくなる
blueクラスの確率とorangeクラスの確率が同程度の時、確信度の絶対値が同程度になり、符号が逆になる
確率に対して確信度は線形ではない

print(data.sort_values(by="prob0", ascending=False))

#        prob0     prob1    pred  dec_func correct
# 6   0.999543  0.000457    blue -7.690972    blue
# 10  0.998442  0.001558    blue -6.462560    blue
# 15  0.984817  0.015183    blue -4.172312  orange
# .....
# 0   0.015736  0.984264  orange  4.135926  orange
# 11  0.013521  0.986479  orange  4.289866  orange
# 4   0.013521  0.986479  orange  4.289866  orange

print(data.sort_values(by="prob0", ascending=False))

# prob0 prob1 pred dec_func correct

# 6 0.999543 0.000457 blue -7.690972 blue

# 10 0.998442 0.001558 blue -6.462560 blue

# 15 0.984817 0.015183 blue -4.172312 orange

# .....

# 0 0.015736 0.984264 orange 4.135926 orange

# 11 0.013521 0.986479 orange 4.289866 orange

# 4 0.013521 0.986479 orange 4.289866 orange

クラス0(blue)に対する確率とdecision_function()の確信度の関係を図示すると以下のようになり、確率に対して確信度が必ずしも線形になっていないことがわかる。

コードはmatplotlib.pyplotをインポートした上で、以下を追加。

prob = np.array(sorted_data["prob0"])
conf = np.array(sorted_data["dec_func"])
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(prob, conf)
ax.grid()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position(('data', 0.5))
ax.set_xlabel("class-0 probaility", loc='left')
ax.set_ylabel("confidence", loc='bottom')
plt.show()

prob = np.array(sorted_data["prob0"])

conf = np.array(sorted_data["dec_func"])

fig = plt.figure()

ax = fig.add_subplot()

ax.plot(prob, conf)

ax.grid()

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position(('data', 0.5))

ax.set_xlabel("class-0 probaility", loc='left')

ax.set_ylabel("confidence", loc='bottom')

plt.show()

決定境界

以下は、predict_proba()で計算された確率を可視化したもので、decision_function()の場合に比べて、直感的にも分かりやすい分布となっている。

コンターに表す値として、30行目でpredict_proba()の結果の0列目、すなわちClass0の確率を取り出している。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

f0min, f0max = -1.5, 1.5
f1min, f1max = -1.75, 1.5

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

X_train, X_test, y_train, y_test =\
    train_test_split(X, y, random_state=0)

gb = GradientBoostingClassifier(random_state=0)
gb.fit(X_train, y_train)

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))
color0, color1 = 'tab:blue', 'tab:orange'

f0 = np.linspace(f0min, f0max, 200)
f1 = np.linspace(f1min, f1max, 200)
f0, f1 = np.meshgrid(f0, f1)
F = np.hstack((f0.reshape(-1, 1), f1.reshape(-1, 1)))

pred = gb.predict(F).reshape(f0.shape)
axs[0].contour(f0, f1, pred, levels=[0.5])
axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

proba = gb.predict_proba(F)[:, 0].reshape(f0.shape)
print(proba.shape)
axs[1].contourf(f0, f1, proba, alpha=0.5, cmap='RdBu')

for ax in axs:
    ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")
    ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")
    ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")
    ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")

    ax.set_xlim(f0min, f0max)
    ax.set_ylim(f1min, f1max)
    ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

handles, labels = axs[0].get_legend_handles_labels()

fig.legend(handles, labels, ncol=4, loc='upper center')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.ensemble import GradientBoostingClassifier

from sklearn.datasets import make_circles

from sklearn.model_selection import train_test_split

f0min, f0max = -1.5, 1.5

f1min, f1max = -1.75, 1.5

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

X_train, X_test, y_train, y_test =\

train_test_split(X, y, random_state=0)

gb = GradientBoostingClassifier(random_state=0)

gb.fit(X_train, y_train)

fig, axs = plt.subplots(1, 2, figsize=(10, 4.8))

color0, color1 = 'tab:blue', 'tab:orange'

f0 = np.linspace(f0min, f0max, 200)

f1 = np.linspace(f1min, f1max, 200)

f0, f1 = np.meshgrid(f0, f1)

F = np.hstack((f0.reshape(-1, 1), f1.reshape(-1, 1)))

pred = gb.predict(F).reshape(f0.shape)

axs[0].contour(f0, f1, pred, levels=[0.5])

axs[0].contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25)

proba = gb.predict_proba(F)[:, 0].reshape(f0.shape)

print(proba.shape)

axs[1].contourf(f0, f1, proba, alpha=0.5, cmap='RdBu')

for ax in axs:

ax.scatter(X_train[y_train==0][:, 0], X_train[y_train==0][:, 1], marker='o', fc=color0, ec='k', label="Train class 0")

ax.scatter(X_test[y_test==0][:, 0], X_test[y_test==0][:, 1], marker='^', fc=color0, ec='k', label="Test Class 0")

ax.scatter(X_train[y_train==1][:, 0], X_train[y_train==1][:, 1], marker='o', fc=color1, ec='k', label="Train class 1")

ax.scatter(X_test[y_test==1][:, 0], X_test[y_test==1][:, 1], marker='^', fc=color1, ec='k', label="Test class 1")

ax.set_xlim(f0min, f0max)

ax.set_ylim(f1min, f1max)

ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)

handles, labels = axs[0].get_legend_handles_labels()

fig.legend(handles, labels, ncol=4, loc='upper center')

plt.show()

3クラス以上の場合

3クラスのirisデータセットにGradientBoostingClassifierを適用し、predict_proba()の出力を見てみる。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from pandas import DataFrame

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(
    iris.data, iris.target, random_state=42)

gbc = GradientBoostingClassifier(learning_rate=0.01, random_state=0)
gbc.fit(X_train, y_train)

pred_proba = gbc.predict_proba(X_test)
df = DataFrame(pred_proba, columns=iris.target_names)
df["decision"] = np.argmax(pred_proba, axis=1)
df["prediction"] = gbc.predict(X_test)
print(df)

import numpy as np

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.ensemble import GradientBoostingClassifier

from pandas import DataFrame

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(

iris.data, iris.target, random_state=42)

gbc = GradientBoostingClassifier(learning_rate=0.01, random_state=0)

gbc.fit(X_train, y_train)

pred_proba = gbc.predict_proba(X_test)

df = DataFrame(pred_proba, columns=iris.target_names)

df["decision"] = np.argmax(pred_proba, axis=1)

df["prediction"] = gbc.predict(X_test)

print(df)

このコードの出力結果は以下の通り。3つのクラスに対する確率が得られ、合計は1になる。こちらはdecision_function()が2クラスの時だけ配列が1次元となるのと違って、どのような場合でも行数×列数＝データ数×クラス数の配列になる。

なお17行目で、argmaxを使って各データで確率が最大となるクラスを探している。

      setosa  versicolor  virginica  decision  prediction
0   0.102177    0.788400   0.109422         1           1
1   0.783471    0.109367   0.107161         0           0
2   0.098181    0.110059   0.791761         2           2
3   0.102177    0.788400   0.109422         1           1
4   0.103600    0.667239   0.229161         1           1
.....
33  0.783471    0.109367   0.107161         0           0
34  0.783471    0.109367   0.107161         0           0
35  0.101941    0.115024   0.783035         2           2
36  0.102177    0.788400   0.109422         1           1
37  0.783471    0.109367   0.107161         0           0

setosa versicolor virginica decision prediction

0 0.102177 0.788400 0.109422 1 1

1 0.783471 0.109367 0.107161 0 0

2 0.098181 0.110059 0.791761 2 2

3 0.102177 0.788400 0.109422 1 1

4 0.103600 0.667239 0.229161 1 1

.....

33 0.783471 0.109367 0.107161 0 0

34 0.783471 0.109367 0.107161 0 0

35 0.101941 0.115024 0.783035 2 2

36 0.102177 0.788400 0.109422 1 1

37 0.783471 0.109367 0.107161 0 0

Axes.set_xlabel/ylabel～軸のラベル

2020-09-08 / tau / コメントする

概要

Axesに描いたグラフの軸にラベルを付けるには、set_xlabel()やset_ylabel()を使う。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi)
y = np.sin(x * 2)

fig = plt.figure()
ax = fig.add_subplot()
ax.plot(x, y)
ax.set_xlabel("theta")
ax.set_ylabel("sine")
plt.show()

import numpy as np

import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi)

y = np.sin(x * 2)

fig = plt.figure()

ax = fig.add_subplot()

ax.plot(x, y)

ax.set_xlabel("theta")

ax.set_ylabel("sine")

plt.show()

位置等の調整

ラベルの位置はlocパラメーターで調整する。x軸とy軸では設定値が異なる（matplotlibのバージョンが3.1.1ではエラーになるので、3.3.1にアップグレード）。

set_xlabel("labelname", loc='left'/'center'/'right')
set_ylabel("labelname", loc='bottom'/'center'/'top')

以下の例では、set_ylabel()のパラメーターにTextのプロパティーとしてrotationを指定している（そのままだと横にしたラベルがエリア外に切れてしまうので、8行目でsubplots_adjustを指定している）。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi)
y = np.sin(x * 2)

fig, ax = plt.subplots()
fig.subplots_adjust(left=0.2)
ax.plot(x, y)
ax.set_xlabel("theta", loc='right')
ax.set_ylabel("sine", loc='top', rotation='horizontal')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

x = np.linspace(-np.pi, np.pi)

y = np.sin(x * 2)

fig, ax = plt.subplots()

fig.subplots_adjust(left=0.2)

ax.plot(x, y)

ax.set_xlabel("theta", loc='right')

ax.set_ylabel("sine", loc='top', rotation='horizontal')

plt.show()

複利計算

2020-09-05 / tau / コメントする

概要

複利計算でいろいろなサイトを見るが、どれも前提なしで話を始めたりいきなりExcelの関数を使ったりするものばかりで、スタートラインからどう考えているのかを説明するものにあたらなかった（きっとあるのだろうけれど）。

なので、自分なりの頭の整理のために一から組み立ててみる。

預金の複利計算

一時払い

一時払いは、最初に一定金額を預けた後は預金口座に手を触れずに、満期や解約の時にいくらになるかというもので、これは比較的わかりやすい。たとえば年率1%の預金に100万円を預けたら10年後にいくらになっているか、というような計算。表計算で計算すると以下のようになる。

このとき、以下のような仕組みだということを明記しておく。

期首の途中に預けても、期末までに年利率がすべて適用される（日割りなどはされない）
その年利率を適用した利子が期首金額に加えられ、翌期の期首金額となる
毎年の利子の計算の際、小数点以下は切り落としている

これくらいだと、元本に対して利率1%を定額で10年適用した結果と変わらない。ところが50年も置いておくと最終金額は16,443円になり、定額の15,000円との乖離が大きくなってくる。

年利率を2%にすると様相が変わってきて、10年後の利子は2,186円、50年後には利子分で16,873円になる。

50年間の預金額の変化を1%、2%の定額と複利で比較してみると以下のようになる。

所謂指数関数で、利率が大きくなると、あるいは期間が長くなるとカーブの上がり方が急になる。

こういった計算は高校で数列を習うと教えてくれる。たとえば上の例で、預入金額をa、年利率をRとするとn年目の期末残高bは以下のように表される。

(1) $\begin{equation*} b = a (1+R)^n \end{equation*}$

この式に上の金額や利率、年数を入れると同じ結果が出ることが確認できる。式で計算した方が数円額が大きくなるが、これは表計算の際に端数を切り落としたのに対して、数式では丸めずに計算するからである。

積立て

たとえば毎年10万円を積み立てながら年利率1%を適用した時にどうなるか。この場合は、前期末の金額に積立額を加えた額が期首金額となり、以下のような結果になる。

これを定式化するのに次のように考える。毎月a円を積み立てるとして1年目の期末金額b₁は、

(2) $\begin{equation*} b_1 = a (1+R) \end{equation*}$

2年目の期末残高は、この期末残高にa円を加えて利率を適用するので、

(3) $\begin{equation*} b_2 = (b_1 + a) (1+R) = \left( a (1+R) + a \right) (1+R) = a(1+R) + a(1+R)^2 \end{equation*}$

これをn年目まで繰り返すと、最終的な残高は以下のようになる。各月に預けた額ごとに、現在までの利子が複利で適用されて積み重なっているのが表現されている。

(4) $\begin{equation*} b_n = a (1+R) + a (1+R)^2 + \cdots + a(1+R)^n \end{equation*}$

これは初項がa (1 + R)、公比が1 + Rの等比数列の和になるので、預金残高は以下の式で計算できる。

(5) $\begin{align*} b_n &= a (1+R) \frac{1 - (1+R)^n}{1 - (1+R)} = a(1+R) \frac{(1+R)^n - 1}{R} \\ &=a \frac{(1+R)^{n+1} - R - 1}{R} \end{align*}$

借金の複利計算

元利均等返済方式

借金を返す場合、期首に残っている額に利子を掛けた要返済額から各期の返済額を引いた額が翌期首の残額となる。利率は年率表示だが、返済は月ごととし、月利率＝年利率÷12とする。

年利3%で120万円を借り入れて、毎月返済して12か月で返すケースを考え、月ごとの額を同額としたいとする。試みに、120万円に利子がつかないとすると毎月10万円を返せばいいが、この場合は積み重なっていく利子の分だけ返しきれない。

次に120万円に対して12か月間の月利率を複利で適用すると120×1.0025¹²≒123万6500円。これを12か月で割ると、突き当りの返済額は約1万3千円となる。これは毎月の返済を全くしない想定なので、実際に借入残高が減っていくのに対して返しすぎることになる。

この2つの値の間で二分法で答えを探していくと、以下の額に到達する。この時の利子の総額は19,584円で、借り入れの利回りは約1.632%になる。

これを数式で表現してみる。借入額をa、月利をr、返済額pとすると、一月目の借入残額b₁は、

(6) $\begin{equation*} b_1 = a (1+r) - p \end{equation*}$

二月目の借入残額b₂は、一月目の残額に月利を適用してから返済するので、

(7) $\begin{align*} b_2 &= b_1 (1+r) - p = \left( a (1+r) - p \right) (1+r) - p \\ &= a (1+r)^2 - p (1+r) - p \end{align*}$

これは、n月までに借入額に複利で計算した額に対して、返す方も毎月の月数に応じた複利で足し上げて返しますよということになる。これをn月後まで続けた残額b_nは以下のようになる。

(8) $\begin{align*} b_n &= a (1+r)^n - p (1+r)^{n-1} - \cdots - p \\ &= a (1+r)^n - p \frac{1 - (1+r)^n}{1 - (1+r)} \\ &= a (1+r)^n - p \frac{(1+r)^n - 1}{r} \end{align*}$

n月目で残額がゼロとなるようにすると、毎月の返済額pは以下で表される。

(9) $\begin{align*} p = a (1+r)^n \frac{r}{(1+r)^n - 1} \end{align*}$

先ほどの計算では手計算で収束させたが、利率が与えられたときの元利均等の返済額は解析的に求めることができる。表計算ソフトの関数も、この煩雑な関数をシンプルに表現しているに過ぎない。

元本均等方式

元金均等方式は借入額を返済期数で割って均等とし、これに毎期の発生する利子を加えて返済する。この場合の利子総額は19,500円で、借り入れ利回りは1.625%となる。

借入額をa、借り入れ期数をm、月利をr、一月目の借入利子i₁とすると、残額b₁は、

(10) $\begin{equation*} b_1 = a (1+r) - \frac{a}{m} - ar = a - \frac{a}{m} \end{equation*}$

二月目の残額b₂は、

(11) $\begin{equation*} b_2 = b_1 (1+r) - \frac{a}{m} - b_1 r = b_1 - \frac{a}{m} = a - 2 \frac{a}{m} \end{equation*}$

これを繰り返してn月目の残額は、

(12) $\begin{equation*} b_n = a - n \frac{a}{m} \end{equation*}$

n期目の利子額i_nは、n − 1期末の残額に利率を適用して、以下で計算される。

(13) $\begin{equation*} i_n = \left( a - (n - 1) \frac{a}{m} \right) r \end{equation*}$

アドオン方式

この方法は、単利計算に相当し、元本とそれに対する利子の総額を期数で割って均等化した額を返済する。利率は年率を用いて利子を計算し、これを月ごとに均等に割る。これまでの例で計算すると、利子総額は36,000円で、借り入れ利回りは3%。

毎月の返済額pは、借入額aに年利Rをそのまま適用して期数mで割ればよい。

(14) $\begin{equation*} p = \frac{a (1 + R)}{m} \end{equation*}$

比較

元利均等方式は、初期の残額が大きいときの利子を後期に分担させて返済額を均等にする。返済計画が明瞭になるため、一般的なローンに用いられる。

これに対して元本均等方式は初期の残額に対する利子をそのまま負担するので、元利均等方式に比べて初期の利払いが多くなる。逆に早い段階から大きな額で返済していくため、トータルの利払いは元本均等方式の方が元利均等方式よりも少なくなる。企業の資金借入れはこの方法が多い。

アドオン方式は返済中の元利の減少を全く考慮しないため、利払いが最も大きくなる。毎月の返済額が一定で計算も簡単なため、割賦販売の場合に用いられる。

数値

整数

実数

有理数

複素数

文字列

文字リテラル

ヒアドキュメント

論理値

概要

基本のデータ

定義

医学・疫学上の指標

陽性率／陰性率

的中率

有病率／陽性率など

補足：感度と特異度について

補足：「特異度」という表現について

ここで定義する記号

条件付確率による表示

感度／特異度（真陽性率／真陰性率）

偽陽性率／偽陰性率

陽性的中率／陰性的中率

実際の使われ方

概要

有病率

罹患率／発生率

有病率と罹患率（発生率）

どういうときにどちらを使うか

有病率

罹患率

PCR検査？

まとめ

概要

predict_proba()の挙動

decision_function()との比較

決定境界

3クラス以上の場合

概要

位置等の調整

概要

預金の複利計算

一時払い

積立て

借金の複利計算

元利均等返済方式

元本均等方式

アドオン方式

比較

`predict_proba()`の挙動

`decision_function()`との比較