チェビシェフの不等式は何がありがたいかというと、「確率分布がどのようなものであっても、平均と分散の値さえわかっていれば、確率変数の値が平均からはずれる確率がいくら以下か計算できる」ということにある。
たとえばあるデータの平均が![]() 、分散が
、分散が![]() とわかっているとき、データが
とわかっているとき、データが![]() から
から![]() より外れる確率が少なくともどの程度以下か(あるいはその範囲に収まる確率が少なくともどの程度以上か)、というのを教えてくれる。
より外れる確率が少なくともどの程度以下か(あるいはその範囲に収まる確率が少なくともどの程度以上か)、というのを教えてくれる。
チェビシェフの不等式は、以下のようにいくつかの表し方がある
(1) ![]()
ここで![]() とおけば、
とおけば、
(2) ![]()
これを余事象で表すと、
(3) ![]()
ただし、これらの式において![]() 。
。
この不等式の意義は、確率変数がどのような確率分布に従っているとしても成り立つところにある。ただし、その過程で相当の”切り落とし”をしているので実用的な精度ではない。
たとえば母集団が標準正規分布に従う場合、![]() に対して0.9545、0.9973であるのに対して、チェビシェフの不等式では
に対して0.9545、0.9973であるのに対して、チェビシェフの不等式では![]() となる確率は
となる確率は![]() に対して、
に対して、![]() 以上となる。
以上となる。
証明:離散確率
離散確率で、![]() の値に応じて確率変数を以下のように区分する。
の値に応じて確率変数を以下のように区分する。
(4) ![]()
また、以下の確率分布を定義する。
(5) ![]()
このとき、以下が成り立つ。
(6) 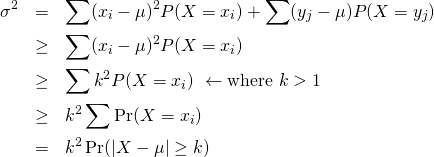
(7) ![]()
証明:連続確率
確率の定義から以下が成り立つ。
(8) ![]()
ここで、以下のように変数を変換する。
(9) ![]()
これより、以下が成り立つ。
(10) 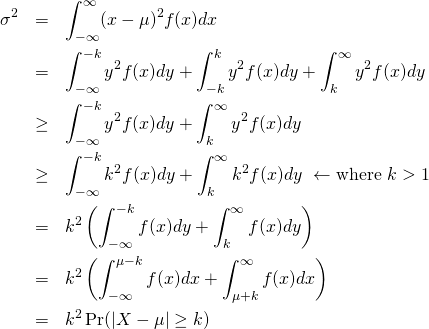
(11) ![]()