Ridge回帰とLasso回帰

1 概要
2 Ridge回帰
3 Lasso回帰
4 Ridge回帰とLasso回帰の挙動
- 4.1 係数の大きさ
- 4.2 学習曲線

概要

回帰は、以下のようなm個の特徴量に関するnセットのデータXとそれらに対するターゲット値yについて、xからyを推定するモデルを決定する。

(1) $\begin{equation*} \boldsymbol{X} = \left[ \begin{array}{ccc} x_{11} & \cdots & x_{m1} \\ \vdots & & \vdots \\ x_{1n} & \cdots & x_{mn} \\ \end{array} \right] \left[ \begin{array}{c} y_1 \\ \vdots \\ y_n \end{array} \right] \quad \Rightarrow \quad y = f(\boldsymbol{x}) \end{equation*}$

線形回帰は、モデルの関数形を以下のような特徴量に関する線形式とする。

(2) $\begin{equation*} \hat{y} = w_0 + w_1 x_1 + \cdots + w_m x_m \end{equation*}$

通常線形回帰（重回帰、多重回帰）の場合、これを以下のような最小化問題として解く。

(3) $\begin{equation*} \mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i)^2 \end{equation*}$

通常線形回帰では、全ての訓練データに対する予測誤差を最小化しようとするが、このことで大きく外れた特徴量に対しても何とか合わせようとすることになる。このような状態を過学習と呼び、訓練データに対する予測精度は高くなるが、モデルが訓練データの状態に過敏に反応して、全般的な特徴に対する精度が却って低くなる（過学習～多項式回帰の場合）。

そこで、通常線形回帰の最適化に対して、全体的に重み係数の影響を小さくするための正則化項（罰金項、ペナルティー項）を考慮する。通常、ペナルティー項としては重み係数のノルムが用いられる（右辺第1項や第2項に分数の係数をつけることがあるが、計算の便宜のためであり本質への影響はない）。

(4) $\begin{equation*} \mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i) + \alpha \sum_j |w_j|^p \end{equation*}$

正則化項が重みの大きさを制限しようとするものであること、この式がこれを制約とした制約条件付き最適化問題であることは正則化の意味にまとめた。

このノルムにおいて、p=1(L1ノルム)の場合をLasso回帰、p=2(L2ノルム)の場合をRidge回帰と呼び、重みに対する制限のほかに以下のような特徴がある。

Ridge回帰: 特徴量間の相関が高い場合～多重共線性(multicolinearity)が強い場合や一時従属な場合、通常線形回帰では解が求まらなかったりモデルが不安定になるが、Ridge回帰は何とか解を求められるようになる。
Lasso回帰: 多数の特徴量のうち効果が小さいものの係数がゼロになり、モデルの複雑さを緩和できる。

Ridge回帰

Ridge回帰は、多重線形回帰の最適化において重み係数のL2ノルムを正則化項として付加する。

(5) $\begin{align*} &\mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i) + \alpha \sum_j |w_j|^2 \\ & \mathrm{where} \quad \hat{y}_i = w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} \end{align*}$

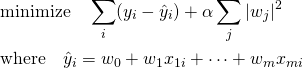
Ridge回帰は、特徴量の重みの強さを制限する（係数の絶対値を小さくする）効果を持つとともに、特徴量間の線形性が強い場合は予測式が不安定になることを防ぐ。

Ridge回帰の解析的な理解

Lasso回帰

Lasso回帰は、多重線形回帰の最適化において重み係数のL1ノルムを正則化項として付加する。

(6) $\begin{align*} &\mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i) + \alpha \sum_j |w_j| \\ & \mathrm{where} \quad \hat{y}_i = w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} \end{align*}$

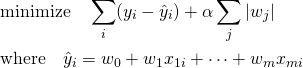
Lasso回帰もRidge回帰と同じく、特徴量の係数の重みを制限するが、正則化を強めるとともに係数がゼロとなり、モデルがシンプルになるという特性がある。

Lasso回帰の解析的な理解

Ridge回帰とLasso回帰の挙動

係数の大きさ

Pythonのscikit-learnで得られる糖尿病に関するdiabetesデータセットを使って、同じくscikit-learnのRidge回帰モデルとLasso回帰モデルの挙動を比べてみる。alphaを大きくして正則化を強めるほど、全体的に係数の絶対値が小さくなっている。Ridgeの場合は必ずしも係数をゼロにしないのでモデルの複雑さが残るのに対して、Lassoの場合、係数は正則化が強いほど多くの係数がゼロになりモデルがシンプルになる。

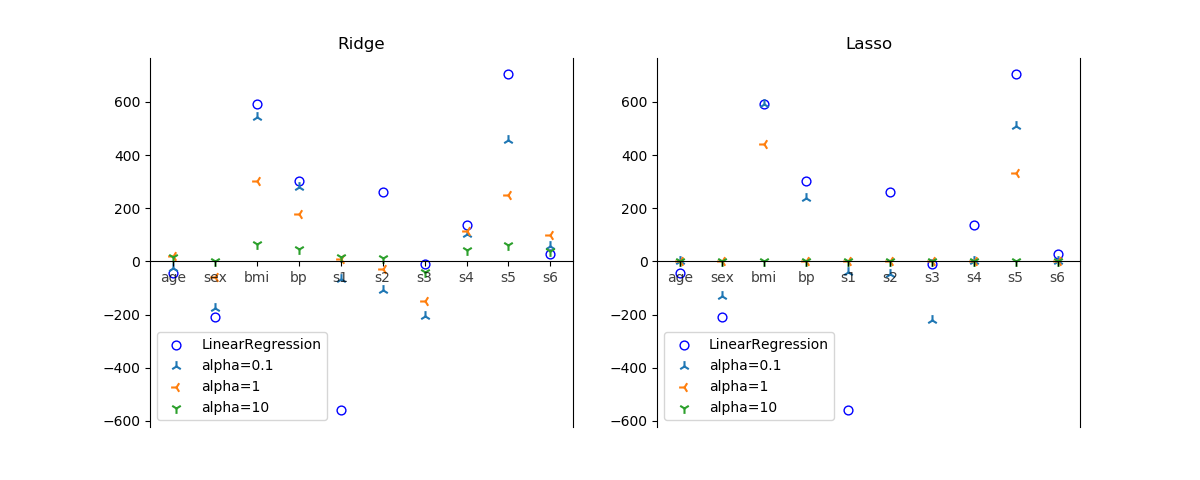
alphaの増加に伴うRidgeのスコアは以下の通りで、そもそも訓練データに対するスコアが低い。もともと10個程度の特徴量ではそれほどの精度が期待できないようだ。

LinearRegression
 training score: 0.555
 test score    : 0.359
Ridge(alpha=0.1)
 training score: 0.550
 test score    : 0.369
Ridge(alpha=1)
 training score: 0.463
 test score    : 0.357
Ridge(alpha=10)
 training score: 0.171
 test score    : 0.143

LinearRegression

training score: 0.555

test score : 0.359

Ridge(alpha=0.1)

training score: 0.550

test score : 0.369

Ridge(alpha=1)

training score: 0.463

test score : 0.357

Ridge(alpha=10)

training score: 0.171

test score : 0.143

Lassoのスコアも同様に低い。alpha=10ではLasso回帰の特性から全ての係数がゼロとなり、相関係数がゼロとなっている。

Lasso(alpha=0.1)
 training score: 0.548
 test score    : 0.355
Lasso(alpha=1)
 training score: 0.414
 test score    : 0.278
Lasso(alpha=10)
 training score: 0.000
 test score    : -0.000

Lasso(alpha=0.1)

training score: 0.548

test score : 0.355

Lasso(alpha=1)

training score: 0.414

test score : 0.278

Lasso(alpha=10)

training score: 0.000

test score : -0.000

この計算に用いたPythonのコードは以下の通り。

import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso

alphas = [0.1, 1, 10]
markers = ['2', '3', '1']

ds = load_diabetes()

X_train, X_test, y_train, y_test =\
    train_test_split(ds.data, ds.target, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)
print("LinearRegression")
print(" training score: {:5.3f}".format(lr.score(X_train, y_train)))
print(" test score    : {:5.3f}".format(lr.score(X_test, y_test)))

fig = plt.figure(figsize=(12, 4.8))
x_scatter = list(range(len(ds.feature_names)))

ax1 = fig.add_subplot(121)
ax1.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',
    label="LinearRegression")
for alpha, marker in zip(alphas, markers):
    rg = Ridge(alpha=alpha)
    rg.fit(X_train, y_train)
    print("Ridge(alpha={})".format(alpha))
    print(" training score: {:5.3f}".format(rg.score(X_train, y_train)))
    print(" test score    : {:5.3f}".format(rg.score(X_test, y_test)))
    ax1.scatter(x_scatter, rg.coef_, marker=marker, s=60,
        label="alpha={}".format(alpha))
    ax1.spines['top'].set_visible(False)
    ax1.spines['bottom'].set_position('zero')
    ax1.set_xticks(x_scatter)
    ax1.set_xticklabels(ds.feature_names, alpha=0.75)
ax1.legend()
ax1.set_title("Ridge")

ax2 = fig.add_subplot(122)
ax2.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',
    label="LinearRegression")
for alpha, marker in zip(alphas, markers):
    ls = Lasso(alpha=alpha)
    ls.fit(X_train, y_train)
    print("Lasso(alpha={})".format(alpha))
    print(" training score: {:5.3f}".format(ls.score(X_train, y_train)))
    print(" test score    : {:5.3f}".format(ls.score(X_test, y_test)))
    ax2.scatter(x_scatter, ls.coef_, marker=marker, s=60,
        label="alpha={}".format(alpha))
    ax2.spines['top'].set_visible(False)
    ax2.spines['bottom'].set_position('zero')
    ax2.set_xticks(x_scatter)
    ax2.set_xticklabels(ds.feature_names, alpha=0.75)
ax2.legend()
ax2.set_title("Lasso")

plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import load_diabetes

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.linear_model import Ridge

from sklearn.linear_model import Lasso

alphas = [0.1, 1, 10]

markers = ['2', '3', '1']

ds = load_diabetes()

X_train, X_test, y_train, y_test =\

train_test_split(ds.data, ds.target, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("LinearRegression")

print(" training score: {:5.3f}".format(lr.score(X_train, y_train)))

print(" test score : {:5.3f}".format(lr.score(X_test, y_test)))

fig = plt.figure(figsize=(12, 4.8))

x_scatter = list(range(len(ds.feature_names)))

ax1 = fig.add_subplot(121)

ax1.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',

label="LinearRegression")

for alpha, marker in zip(alphas, markers):

rg = Ridge(alpha=alpha)

rg.fit(X_train, y_train)

print("Ridge(alpha={})".format(alpha))

print(" training score: {:5.3f}".format(rg.score(X_train, y_train)))

print(" test score : {:5.3f}".format(rg.score(X_test, y_test)))

ax1.scatter(x_scatter, rg.coef_, marker=marker, s=60,

label="alpha={}".format(alpha))

ax1.spines['top'].set_visible(False)

ax1.spines['bottom'].set_position('zero')

ax1.set_xticks(x_scatter)

ax1.set_xticklabels(ds.feature_names, alpha=0.75)

ax1.legend()

ax1.set_title("Ridge")

ax2 = fig.add_subplot(122)

ax2.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',

label="LinearRegression")

for alpha, marker in zip(alphas, markers):

ls = Lasso(alpha=alpha)

ls.fit(X_train, y_train)

print("Lasso(alpha={})".format(alpha))

print(" training score: {:5.3f}".format(ls.score(X_train, y_train)))

print(" test score : {:5.3f}".format(ls.score(X_test, y_test)))

ax2.scatter(x_scatter, ls.coef_, marker=marker, s=60,

label="alpha={}".format(alpha))

ax2.spines['top'].set_visible(False)

ax2.spines['bottom'].set_position('zero')

ax2.set_xticks(x_scatter)

ax2.set_xticklabels(ds.feature_names, alpha=0.75)

ax2.legend()

ax2.set_title("Lasso")

plt.show()

学習曲線

特徴量を増やすために、Boston house-pricesデータセットの特徴量データを拡張して試す。13個の特徴量に加えて、それらの特徴量同士の積から新たな特徴量を生成する。その結果、全体の特徴量数は単独の特徴量13、各特徴量の2乗が13、2つの特徴量の積が₁₃C₂ = 78の合計で104個となる。この特徴量データとターゲットの住宅価格について訓練データとテストデータに分け、Ridge回帰とLasso回帰のハイパーパラメータalphaを変化させてスコアの変化を見たのが以下の図。

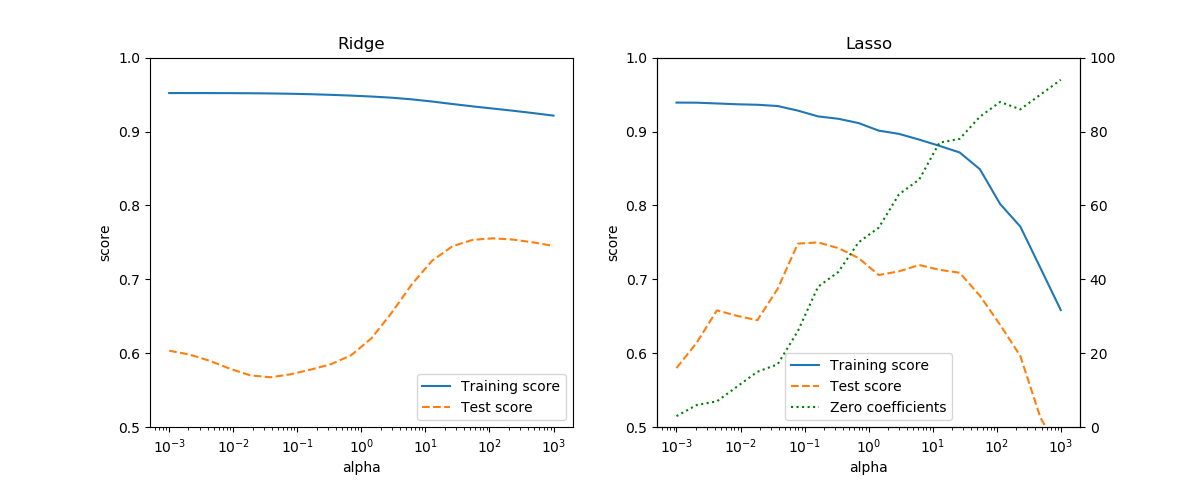
Ridge、Lassoとも訓練データのスコアに対してテストデータのスコアは低く、過学習の様子がわかる。Ridgeではalpha=100程度でテストデータのスコアが最も高く0.75程度となる。Lassoの方はalpha=0.1程度でテストデータのスコアが最も高く、これも0.75を少し上回る程度。またLassoについては、alphaを増やしていくとゼロとなる係数の数が増えていき、それに伴って訓練データのスコアも下がっている。

Boston house-pricesデータに対して、RidgeとLassoの2つのモデルのみを検討するなら、計算コストがより少ないLasso回帰でalpha=0.1程度を選択することになろうかと考えられる。

この計算のコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso

pow_min = -3
pow_max = 3
pow_num = 20
alpha_exp = np.linspace(pow_min, pow_max, pow_num)
alphas = 10**alpha_exp

ds = load_boston()
X_org = ds.data
y = ds.target

cols = X_org.shape[1]
X = X_org.copy()
for j in range(cols):
    for jj in range(j + 1):
        X = np.hstack((X, (X[:, j] * X[:, jj]).reshape(-1, 1)))

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))

trn_scores_ridge = np.empty(0)
tst_scores_ridge = np.empty(0)
for alpha in alphas:
    rg = Ridge(alpha=alpha)
    rg.fit(X_train, y_train)
    trn_scores_ridge = np.append(trn_scores_ridge, rg.score(X_train, y_train))
    tst_scores_ridge = np.append(tst_scores_ridge, rg.score(X_test, y_test))

trn_scores_lasso = np.empty(0)
tst_scores_lasso = np.empty(0)
zero_coef = np.empty(0)
n_zero_coef = np.empty(0)
for alpha in alphas:
    ls = Lasso(alpha=alpha)
    ls.fit(X_train, y_train)
    trn_scores_lasso = np.append(trn_scores_lasso, ls.score(X_train, y_train))
    tst_scores_lasso = np.append(tst_scores_lasso, ls.score(X_test, y_test))
    n_zero_coef = np.append(n_zero_coef, ls.coef_[ls.coef_==0].size)

fig = plt.figure(figsize=(12, 4.8))

ax_ridge = fig.add_subplot(121)
ax_ridge.plot(alphas, trn_scores_ridge, label="Training score")
ax_ridge.plot(alphas, tst_scores_ridge, linestyle='dashed', label="Test score")
ax_ridge.set_xscale('log')
ax_ridge.set_ylim(0.5, 1)
ax_ridge.set_xlabel("alpha")
ax_ridge.set_ylabel("score")
ax_ridge.legend()
ax_ridge.set_title("Ridge")

ax_lasso = fig.add_subplot(122)
ax_lasso_coef = ax_lasso.twinx()
ax_lasso.plot(alphas, trn_scores_lasso, label="Training score")
ax_lasso.plot(alphas, tst_scores_lasso, linestyle='dashed', label="Test score")
hscore, lscore = ax_lasso.get_legend_handles_labels()
ax_lasso_coef.plot(alphas, n_zero_coef, linestyle='dotted',
    label="Zero coefficients", c='g')
hcoef, lcoef = ax_lasso_coef.get_legend_handles_labels()
ax_lasso.set_xscale('log')
ax_lasso.set_ylim(0.5, 1)
ax_lasso_coef.set_ylim(0, 100)
ax_lasso.set_xlabel("alpha")
ax_lasso.set_ylabel("score")
ax_lasso.legend(hscore + hcoef, lscore + lcoef, loc='lower center')
ax_lasso.set_title("Lasso")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.linear_model import Ridge

from sklearn.linear_model import Lasso

pow_min = -3

pow_max = 3

pow_num = 20

alpha_exp = np.linspace(pow_min, pow_max, pow_num)

alphas = 10**alpha_exp

ds = load_boston()

X_org = ds.data

y = ds.target

cols = X_org.shape[1]

X = X_org.copy()

for j in range(cols):

for jj in range(j + 1):

X = np.hstack((X, (X[:, j] * X[:, jj]).reshape(-1, 1)))

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print(lr.score(X_train, y_train))

print(lr.score(X_test, y_test))

trn_scores_ridge = np.empty(0)

tst_scores_ridge = np.empty(0)

for alpha in alphas:

rg = Ridge(alpha=alpha)

rg.fit(X_train, y_train)

trn_scores_ridge = np.append(trn_scores_ridge, rg.score(X_train, y_train))

tst_scores_ridge = np.append(tst_scores_ridge, rg.score(X_test, y_test))

trn_scores_lasso = np.empty(0)

tst_scores_lasso = np.empty(0)

zero_coef = np.empty(0)

n_zero_coef = np.empty(0)

for alpha in alphas:

ls = Lasso(alpha=alpha)

ls.fit(X_train, y_train)

trn_scores_lasso = np.append(trn_scores_lasso, ls.score(X_train, y_train))

tst_scores_lasso = np.append(tst_scores_lasso, ls.score(X_test, y_test))

n_zero_coef = np.append(n_zero_coef, ls.coef_[ls.coef_==0].size)

fig = plt.figure(figsize=(12, 4.8))

ax_ridge = fig.add_subplot(121)

ax_ridge.plot(alphas, trn_scores_ridge, label="Training score")

ax_ridge.plot(alphas, tst_scores_ridge, linestyle='dashed', label="Test score")

ax_ridge.set_xscale('log')

ax_ridge.set_ylim(0.5, 1)

ax_ridge.set_xlabel("alpha")

ax_ridge.set_ylabel("score")

ax_ridge.legend()

ax_ridge.set_title("Ridge")

ax_lasso = fig.add_subplot(122)

ax_lasso_coef = ax_lasso.twinx()

ax_lasso.plot(alphas, trn_scores_lasso, label="Training score")

ax_lasso.plot(alphas, tst_scores_lasso, linestyle='dashed', label="Test score")

hscore, lscore = ax_lasso.get_legend_handles_labels()

ax_lasso_coef.plot(alphas, n_zero_coef, linestyle='dotted',

label="Zero coefficients", c='g')

hcoef, lcoef = ax_lasso_coef.get_legend_handles_labels()

ax_lasso.set_xscale('log')

ax_lasso.set_ylim(0.5, 1)

ax_lasso_coef.set_ylim(0, 100)

ax_lasso.set_xlabel("alpha")

ax_lasso.set_ylabel("score")

ax_lasso.legend(hscore + hcoef, lscore + lcoef, loc='lower center')

ax_lasso.set_title("Lasso")

plt.show()

TauStation

Ridge回帰とLasso回帰

概要

Ridge回帰

Lasso回帰

Ridge回帰とLasso回帰の挙動

係数の大きさ

学習曲線

コメントを残すコメントをキャンセル

概要

Ridge回帰

Lasso回帰

Ridge回帰とLasso回帰の挙動

係数の大きさ

学習曲線

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル