ベクトルの内積の表現には、要素表示を用いたものと幾何的なものの2つがある。
![]()
2つの表現が等価であることを証明するのに、下図のように2つのベクトルで張られた三角形の![]() の長さを考える。
の長さを考える。
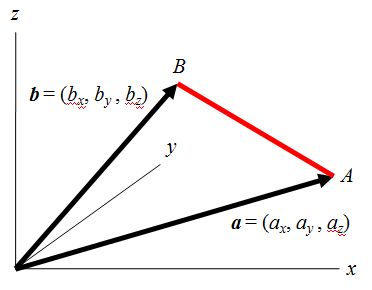
まずベクトルの成分で計算した場合は、
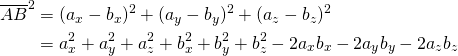
また余弦定理を用いて計算した場合は、![]() として以下のようになる。
として以下のようになる。
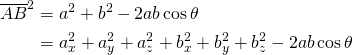
上記2つが等しいことから、以下が得られる。
![]()
2次元の場合は、z成分を0とおいてx成分とy成分のみについて考えればよい。
ベクトルの内積の表現には、要素表示を用いたものと幾何的なものの2つがある。
![]()
2つの表現が等価であることを証明するのに、下図のように2つのベクトルで張られた三角形の![]() の長さを考える。
の長さを考える。

まずベクトルの成分で計算した場合は、
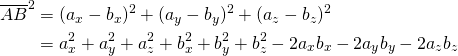
また余弦定理を用いて計算した場合は、![]() として以下のようになる。
として以下のようになる。
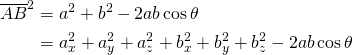
上記2つが等しいことから、以下が得られる。
![]()
2次元の場合は、z成分を0とおいてx成分とy成分のみについて考えればよい。
三角形の2辺a、bとそのなす角θが与えられたとき、3つ目の辺cの長さは以下で求められる。
![]()
下図のように、辺a、bとそのなす角θが与えられているとき、3つ目の辺cとそれらとの関係を考える。
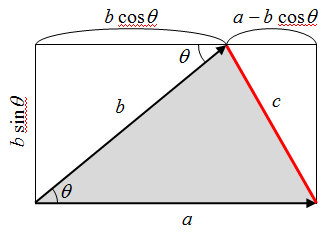
辺cは上図右の直角三角形の斜辺なので、以下の式が成り立つ。
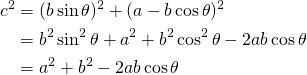
下図のようになす角が鈍角の場合を考える。
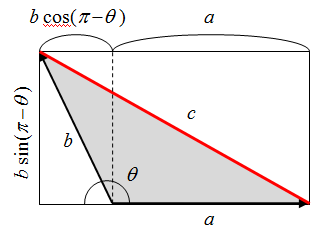
![Rendered by QuickLaTeX.com $$ \begin{align*} c^2 &= \left[ b \sin ( \pi - \theta ) \right]^2 + \left[ b \cos ( \pi - \theta ) + a \right]^2 \\ &= (b \sin \theta )^2 + (-b \cos \theta + a)^2 \\ &= b^2 \sin ^2 \theta + b^2 \cos ^2 \theta + a^2 - 2ab \cos \theta \\ &= a^2 + b^2 - 2ab \cos \theta \end{align} $$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-bbbc758041289d3592c77d7729f346bf_l3.png)
ある点が運動しているとき、着目する他の点が進行方向の前方にあるのか、後方にあるのかを判定したい時があるが、2次元の場合は、ベクトルの内積を使うとこの判定が簡単にできる。
以下の図で、点sがvの方向に進んでいるとき、点pが前方/後方のいずれにあるかを判定する。
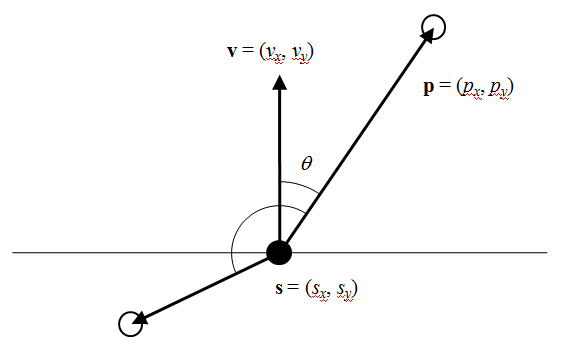
sを起点としたベクトルvと、sから見たpの相対的な位置ベクトルの内積を考えると、
![]()
上式で0≤θ≤90度の範囲であればpはsの前方にあり、このときcosθ≥0。また90度<θ≤180度の範囲ならpはsの後方にあり、cosθ<0となる。
内積を計算する角は、ベクトルvとpのなす角なので、pがsの左右どちらにあるかは問わない。
以上のことから、進行方向のベクトルvと、自身から見た相対的な着目点の位置ベクトルの内積が正なら着目点は前方に、負なら後方にあることになる(ゼロならば真横)。
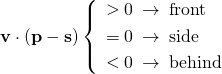
方向ベクトルvを90度回転させた上で上記の前後判定を行うことで左右判定が可能になる。
右へ回転させたベクトルに対して前方なら元の方向ベクトルの右、後方なら元の方向ベクトルの左と判定できる。
2次元の場合、2つのベクトルが平行かどうかを確かめるには、いずれか一方を90度回転させて、それが他のベクトルと直角であるかどうかを確かめるとよい(→ベクトルを90度回転させる方法)。
以下の2つのベクトルが平行かどうかを確認するには、
![]()
たとえば![]() を90度回転させて内積がゼロかどうかを確認する。
を90度回転させて内積がゼロかどうかを確認する。
![]()
なお、この式は、2つのベクトルの外積のx-y平面に垂直な成分(z成分)を計算していることになる。
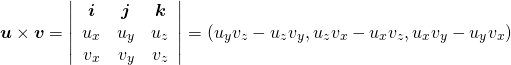
この2次元の2つのベクトルの場合、外積の絶対値はz成分の大きさにほかならず、その値は![]() に対応することから、この値がゼロの場合は
に対応することから、この値がゼロの場合は![]() すなわち平行を意味する。
すなわち平行を意味する。
なお数値計算上は、内積値の絶対値がある小さな値より小さいかどうかを判定することになる。
2つのベクトルが平行な時、そのなす角がゼロとなることから以下が成り立つ。
(1) ![]()
この等式についても、小さな値との比較で判定する。
下図のように互いに直交する2つのベクトルを考える。
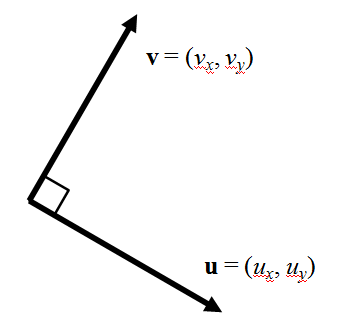
これらのベクトルが直角であるためには、内積がゼロとなればよい。
![]()
成分表示すれば
![]()
これを満足する最もわかりやすいベクトル![]() は、
は、![]() の要素を入れ替えて、何れか片方をマイナスとしたもの。
の要素を入れ替えて、何れか片方をマイナスとしたもの。
![]()
ここで要素を入れ替えた後のy成分をマイナスとしたベクトルは、元のベクトルを90度右に回転させたもので、x成分をマイナスとしたベクトルは、元のベクトルを90度左に回転させたもの。
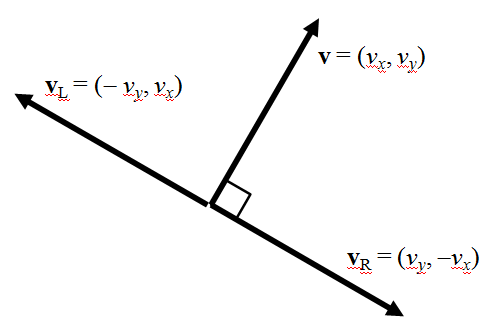
これは回転行列を使って確かめることもできる。ただし以下の式で、+は左回り、-は右回りの回転であることに注意。
![]()
WordPressで整った数式を表示したいとき、MS-Officeの数式エディタの表示を画像として張り付けることを考えたが、探してみると”MathJax-LaTeX”というプラグインがよく紹介されていた。LaTexの書式で書いた数式が整形されて画像として張り付けられるらしい。
MathJax-LaTexはプラグインをインストール後、記事の冒頭にショートコード[mathjax]を書き、そのページ内でLaTexの記述が可能になという手軽なものなので、一度導入して試してみた。
ところが、ショートコードを入れたると$$マークや$マークが数式整形のための記号として認識されてしまう。たとえばjQueryに関する記事中やスクリプトコードで$マークを使うとややこしいことになる。また数式をインラインで書けないとか、テキストモードで複数行にわたる数式を書けないとか、いろいろ制約があるようだ。
そこでほかにもプラグインはないかと探して、以下のサイトに辿り着いた。
“WP QuickLaTex“というプラグインがあるそうで、試しにインストールしてみたところ悪くない。
|
1 |
[latexpage] |
インラインスタイル(![]() のような書き方)の場合は、以下のようにショートコードで囲む。
のような書き方)の場合は、以下のようにショートコードで囲む。
|
1 |
[latex]...[/latex] |
この機能は、冒頭にショートコードを書かなくても使える。
式を別段落で表示させるディスプレイスタイルの書き方には、以下の2つの方法がある。
|
1 |
$$...$$ |
この場合、ショートコード以前の$$マークは無視されるが、ショートコードを書くと記事中の$$マークはQuickLaTexが数式解釈に使う。
|
1 |
[latex]$$...$$[/latex] |
ディスプレイスタイルでは、上記いずれの書き方でも、テキストモードで改行して複数行にわたって記述可能。
結局現在は、ディスプレイスタイルも単に[latex]...[/latex]記号のみで書いている。
|
1 2 3 4 5 |
[latex] \begin{equation} y = a x^2 + b x + c \end{equation} [/latex] |
\begin{align}~\end{align}や\begin{array}{...}~\end[array]で括ると改行される<pre></pre>の場合、表示されない記述例
WP QuickLaTexでLaTex形式の記述がどのように表示されるか列挙する。
{\rm }で斜体を通常書体に、{bf }と\mathbf{}は同じで太字、{\boldmath }は機能しない。いずれもギリシャ文字(小文字)には効かない。
|
1 2 3 4 5 |
abcABC \alpha \beta \gamma \\ {\rm abcABC \alpha \beta \gamma} \\ {\bf abcABC \alpha \beta \gamma} \\ \mathbf{abcABC \alpha \beta \gamma} \\ {\boldmath ab$cABC \alpha$ \beta \gamma} |
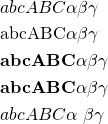
その後、\boldsymbolでアルファベットの大文字・小文字、ギリシャ文字を斜体太字にできることがわかった。
|
1 |
\boldsymbol{abcABC \alpha \beta \gamma} |
![]()
|
1 2 3 4 5 |
a = 1 \\ a \neq 2 \\ a \leq 2 , \: a \leqq 2 \\ a \geq 0 . \: a \geqq 0 \\ a \sim 1.1 , \: a \simeq 1.1 , \: a \approx 1.1 , \:a \fallingdotseq 1.1 |
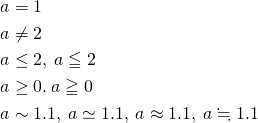
普通の記号
|
1 |
a + b \times c \div d |
![]()
分数の記述は\fracで(分子・分母で\fracを使うと小さくなるので、元のままのサイズにしたいときは\dfracを使う
|
1 |
\frac{\frac{1}{2} + \frac{1}{2}}{\dfrac{1}{3} + \dfrac{1}{3}} |
![]()
分数などに対して背の高い括弧を使うときは、\left(、\right)などを使う。
|
1 |
\left( \frac{1}{2} + \frac{1}{3} \right) \times 6 = 5 |
![]()
|
1 |
z = x \cdot y |
![]()
|
1 2 |
a \pm b a \mp b |
![]()
|
1 2 3 4 |
S = 1 + 2 + \cdots + 100 S = 1 + 2 + \ldots + 100 \vdots \ddots |
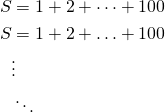
|
1 2 3 4 5 |
\leftarrow \: \Leftarrow \: \longleftarrow \: \Longleftarrow \rightarrow\ \: \Rightarrow \: \longrightarrow \: \Longrightarrow \leftrightarrow \: \Leftrightarrow \: \longleftrightarrow \: \Longleftrightarrow \uparrow \: \Uparrow \: \downarrow \: \Downarrow \nearrow \; \searrow \; \swarrow \: \nwarrow |
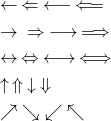
|
1 |
\angle R = 90^\circ |
![]()
latexショートコードだけで囲むと、数式が左詰めになり、式番号なしで数式が表示される。
|
1 2 3 |
[latex] z = x + y [/latex] |
![]()
equation環境では、数式がセンタリングされ、式番号が付けられる。
|
1 2 3 4 5 |
[latex] \begin{equation} z = x + y \end{equation} [/latex] |
![]()
eqnarray環境では、複数式を一つにまとめて扱える。
|
1 2 3 4 5 6 7 8 |
[latex] \begin{eqnarray} (a + b)^2 &=& a(a + b) + b(a + b) \\ &=& a^2 + b^2 + 2ab \\ (a + b)(a - b) &=& a(a - b) + b(a - b) \\ &=& a^2 - b^2 \end{eqnarray} [/latex] |
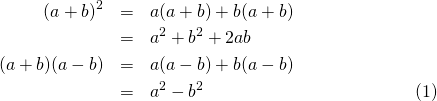
方程式の左を中括弧で囲いたい場合、\left\{とするが、eqnarray環境ではうまくいかない。array環境を使えばよいが、若干の注意点がある。
|
1 2 3 4 5 6 7 8 9 |
[latex] \begin{equation} \left\{ \begin{array}{lll} x + y & = & c \\ x ^2 + y^2 & = & r^2 \right. \end{array} \end{equation} [/latex] |
![]()
単に中央ぞろえで複数行の式を書きたい場合はgather環境が手軽。式番号は自動でつけてくれる(以下の例ではgather*として式番号を抑止している)。
|
1 2 3 4 5 6 7 8 |
[latex] \begin{gather} a x^2 + bx + c = 0 \\ a \left( x + \frac{b}{2a} \right) ^2 - \frac{b^2}{4a} + c = 0\\ x + \frac{b}{2a} = \pm \sqrt{\frac{1}{a} \frac{b^2 - 4ac}{4a}} \\ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \end{gather} [/latex] |
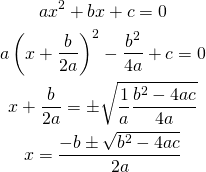
式中の任意の位置でそろえるにはalign環境と&記号を使う。たとえば全体をセンタリングしながらその中で式を左揃えにしたい場合、全ての式の先頭に&記号を置けばけばよい(もちろん、式ごとの揃える位置を変えることもできる)。
|
1 2 3 4 5 6 7 |
[latex] \begin{align} & x^2 + y^2 = r^2 \\ & x = r \cos \theta , y = r \sin \theta \\ & r^2 \cos ^2 \theta + r^2 \sin ^2 \theta = r^2 \end{align} [/latex] |
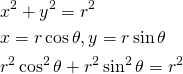
\quad |
|
\qquad |
| \hspace{12pt} | |
| \hspace{1pc} | |
| \hspace{12mm} | |
| \hspace{1.2cm} |
| \! | |
| \, | |
| \: | |
| \; |
\!は負のスペースで、後ろの文字を前へ詰める。
![]() (AとBの間に\!が4つ)
(AとBの間に\!が4つ)
| \phantom{} |
|
1 |
\left| \frac{c+d}{a+b} \right| ^2 = \left( \frac{c+d}{a+d} \right) ^2 = \left\{ \frac{c+d}{a+d} \right\} ^2 |
![]()
|
1 2 |
l = \sqrt{x^2 + y^2} \\ \sqrt[n]{x} |
![]()
\sqrtのn乗根のnは”[n]”と大括弧で、数値xは”{x}”と中括弧で書いている点に注意。
|
1 |
z^n = x^n + y^n |
![]()
|
1 2 3 |
\sin x , \cos x , \tan x \sec x , \csc x , \cot x \arcsin x , \arccos x , \arctan x |
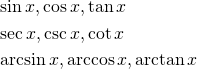
|
1 |
\log_2 x , \log x , \ln x |
![]()
|
1 2 |
S = \sum_{n=1}^{10} n P = \prod_{m=1}^{10} m |
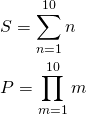
順列・組み合わせのように、記号の前にプレフィックスが付く場合は、ダミーに対してサフィックスを付ける。
|
1 2 3 |
[latex] {}_n P_k , \quad {}_n C_k [/latex] |
![]()
組み合わせを二項係数の形で書く場合は\binomを使う。使い方は\fracと同じで、分数などの中で小さくなるのを避ける場合には\dbinomを使う。
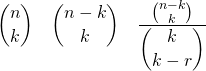
列ベクトルはarray環境でn行1列とする。{c}は各要素を中央ぞろえで、左揃えならl、右揃えならr。
|
1 2 |
\vec{a} = (a_1, \cdots , a_n) {\bf a} = \left( \begin{array}{c} a_1\\ \vdots\\ a_n \end{array} \right) |
![]()
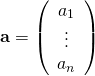
行列はarray環境で
|
1 2 3 4 5 6 7 |
{\bf A} = \left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right] |
![Rendered by QuickLaTeX.com $$ {\bf A} = \left[ \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{array} \right]$$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-385c4a4524601efa3098b5721d3d60a9_l3.png)
QuickLatexでベクトル・行列を太字で表記する方法。
|
1 |
\boldsymbol{Ax} = \lambda \boldsymbol{x} |
![]()
|
1 2 3 4 5 |
[latex] \| \boldsymbol{a} \| \\ \boldsymbol{a} \perp \boldsymbol{b} \\ \boldsymbol{a} \parallel \boldsymbol{b} [/latex] |
![]()
二通りの転置行列の記述方法。
|
1 2 |
{}^t \boldsymbol{A} \\ \boldsymbol{A} ^{\rm T} |
![]()
|
1 |
\frac{dy}{dx} = f'(x) |
![]()
|
1 |
\Delta = \nabla^2 = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} |
![]()
|
1 |
\int_a^b f(x) dx |
![]()
|
1 |
\overbrace{1, 2, 3, 4,}^{\rm over} \underbr = ace{5, 6, 7, 8}_{\rm under} |
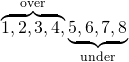
簡単な筆算は、arrayブロックで\hlineを使う。
|
1 2 3 4 5 6 |
\begin{array}{rr} & 12345 \\ + & 678 \\ \hline & 13023 \end{array} |
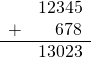
多項式の和になるとちょっとややこしい。
|
1 2 3 4 5 6 |
\begin{array}{rcccccc} A_n &= &a_1 &+ &\cdots &+ &a_n \\ B_n &= &b_1 &+ &\cdots &+ &b_n \\ \hline A_n + B_n &= &(a_1 + b_1) &+ &\cdots &+ &(a_n + b_n) \end{array} |
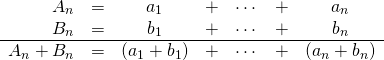
2点間の距離を比較するときに、sqrtといった関数で距離を求める汎用メソッド/関数を使うのに対して、距離の2乗のままで比較して計算スピードを上げることが考えられる。
昔の大型計算機で大きな規模の方程式を解くときなどは、計算スピードを上げるために距離の2乗のままで比較をしていたりしたが、簡単なシミュレーションやアニメーションなどで、それがどれくらい効いてくるのかがよくわからなかった。
そこで、他の関数も含めて、Mathクラスのクラスメソッドとして定義されている浮動小数点系の関数群の実行時間を計ってみた。
加減乗除算の間では実行時間にあまり差はなく、これらを1としたときの各関数の実行時間程度は以下のようになった。
| +-*/ | 1 |
| abs、sqrt、exp、log、random | 1 |
| sin、cos | 2~3 |
| tan、atan | 4~5 |
| atan2 | 5~6 |
| asin、acos | 6~7 |
| pow(**) | 7~8 |
先の結果から、浮動小数点の計算を含むコードに関して、以下のようにまとめられる。
コンソールからテストコードを実行。
ここでa = 1.1、b = -2.2で、各関数の繰り返し回数は100万回。時間の単位はミリ秒。
| a+b | 17 | 17 | 17 |
| a-b | 26 | 26 | 28 |
| a*b | 20 | 18 | 20 |
| a/b | 16 | 17 | 18 |
| a**b | 156 | 157 | 157 |
| abs(a) | 29 | 27 | 30 |
| abs(b) | 30 | 29 | 30 |
| sqrt(a) | 29 | 30 | 31 |
| sin(a) | 71 | 71 | 71 |
| cos(a) | 59 | 61 | 61 |
| tan(a) | 83 | 84 | 84 |
| asin(a) | 125 | 128 | 128 |
| acos(a) | 124 | 127 | 125 |
| atan(a) | 85 | 84 | 87 |
| atan2(a) | 138 | 140 | 146 |
| exp(a) | 15 | 17 | 17 |
| log(a) | 15 | 17 | 18 |
| random(a) | 26 | 27 | 27 |
| a+b | 9 | 10 | 9 |
| a-b | 12 | 11 | 12 |
| a*b | 7 | 9 | 7 |
| a/b | 7 | 7 | 7 |
| a**b | 72 | 71 | 72 |
| abs(a) | 11 | 12 | 17 |
| abs(b) | 12 | 17 | 12 |
| sqrt(a) | 13 | 13 | 13 |
| sin(a) | 27 | 25 | 23 |
| cos(a) | 24 | 25 | 25 |
| tan(a) | 43 | 43 | 42 |
| asin(a) | 53 | 53 | 54 |
| acos(a) | 53 | 50 | 51 |
| atan(a) | 41 | 41 | 41 |
| atan2(a) | 61 | 62 | 58 |
| exp(a) | 7 | 7 | 8 |
| log(a) | 6 | 7 | 7 |
| random(a) | 12 | 13 | 12 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
a = 1.1 b = -2.2 sTime = new Date().valueOf() for i in [1..1000000] x = a + b eTime = new Date().valueOf() console.log("+ #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = a - b eTime = new Date().valueOf() console.log("- #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = a * b eTime = new Date().valueOf() console.log("* #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = a / b eTime = new Date().valueOf() console.log("/ #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = a ** b eTime = new Date().valueOf() console.log("** #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.abs(a) eTime = new Date().valueOf() console.log("abs(+) #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.abs(b) eTime = new Date().valueOf() console.log("abs(-) #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.sqrt(a) eTime = new Date().valueOf() console.log("sqrt() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.sin(a) eTime = new Date().valueOf() console.log("sin() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.cos(a) eTime = new Date().valueOf() console.log("cos() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.tan(a) eTime = new Date().valueOf() console.log("tan() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.asin(a) eTime = new Date().valueOf() console.log("asin() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.acos(a) eTime = new Date().valueOf() console.log("acos() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.atan(a) eTime = new Date().valueOf() console.log("atan() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.atan2(a) eTime = new Date().valueOf() console.log("atan2() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.exp(a) eTime = new Date().valueOf() console.log("exp() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.log(a) eTime = new Date().valueOf() console.log("log() #{eTime - sTime}ms") sTime = eTime for i in [1..1000000] x = Math.random() eTime = new Date().valueOf() console.log("random() #{eTime - sTime}ms") sTime = eTime |
CoffeeScriptで書いたコードが、ローカルでもネット上のWordPressでも動くことを確認したが、Android端末で動かないという事象が発生した。
|
1 |
sgn = Math.sign(val) # Javascript実行時にエラー |
同じ症状がWindowsマシンのExplorerでも起こったので、開発ツールで確認したところ、”Math.signはサポートされていない”とのこと。
調べてみると、JavaScript | MDN(Mozilla Developer Network)のMath.sign()のところでブラウザ実装状況を見ると、
当分、この関数は利用できそうにないので、以下のように値を絶対値で割って取り出すのが手っ取り早い(可読性は悪くなるが)。
|
1 |
sgn = val / Math.abs(val) |
Boidsを構築していくために、以下のような全体構成とした。
個体数をセットするためのinput要素のタイプは”number”とした。こうすることにより、ボックスの右側に値をコントロールする矢印が出たり、最小値の指定などができる。
ボタンはWordPressでonclickを使うと問題が生じるので、HTMLでは単にボタンを表示させるだけとし、リスナについてはコード側で対応する。
canvas要素は書き方によってWordPressで勝手に変更されてしまうので注意。
input要素とcanvasについては、コード側から参照するためのidを付与している。
スクリプトについては、jQueryはWordPress側で読み込まれるとのこと。外部スクリプトファイルは、</body>タグの直前あたりを想定して、WordPressのテキストモードで最後尾にscript要素を書いた。<script type="..." src="..."></script>とテキストモードで書いても、ビジュアルモードを経由すると以下のように書き換えられてしまう。
|
1 2 3 4 5 6 7 8 9 10 |
<!-- Boids 0.5--> <input id="boids05_population" min="1" type="number" value="1" /> <input id="boids05_generate" type="button" value="Generate" /> <canvas id="boids05_canvas" style="background-color: #e0e0e0;" width="400" height="300"> </canvas> <!-- テキストモードで最後尾に以下を追加 --> <script src="../coffee/boids/boids_0_5.js" type="text/javascript">// <![CDATA[ // ]]></script> |
クラスは以下の4つを準備
FieldクラスCreatureクラスClusterクラスControlerクラス異なるバージョンのBoidsを同じページで動かすため、バージョンごとのパッケージに上記4つのクラスを入れることとした。
初めのバージョンに対応したパッケージ名はboids05で、グローバルにアクセスするのはControlerオブジェクトだけとし、Boids05.Controlerを定義している。
そして最後に、このスクリプトファイルが読み込まれたときにボタンに対するリスナを登録するための処理を記述している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# Boidsの準備として、個体を運動させる # Boids 0.5 # 指定した数の個体を発生させ、canvas内のランダムな位置に表示させる Boids05 = {} # パッケージBoids05の本体 do -> # Boidsが活動する空間のクラス # このバージョンでは、canvasオブジェクトの上下左右の座標を持つ長方形 class Field # Boidsの個体を実現するクラス # 位置座標と速度ベクトルの成分を保持する # 自らが活動するFieldクラスのオブジェクトへの参照も保持する class Creature # Boidsの群を管理するクラスで、以下を保持する # ・群を構成する複数の個体 # ・個体を描画するcanvasとそのcontextのオブジェクトを保持する class Cluster # Boidsアプリケーションの動作を統括するクラス # Creatureや class Controler # Boids 0.5で用いるための名前空間を設定 Boids05.Controler = Controler # Boids 0.5に対応したDOMの操作に対応し、このパッケージを操作する # DOMがすべて読み込まれてから以下を実行するよう保証 jQuery ($) -> |
jQueryの構文を用いている。WordPressでjQueryを用いる場合、”$”が別のエイリアスに定義されているらしいので、1行目のように書くとのこと。
1つ目のブロックではcanvas要素のDOMオブジェクトを取得し、controlerオブジェクトを生成して初期値をセットしている。
この段階では速度関係は必要ないが、次のステップの前にとりあえず実装したため、Controler.setVMax()メソッドを読んでいる。
2つ目のブロックでは、ボタンが押されたときの処理を記述しており、numberボックスから値を読み込み、それに基づいて個体生成の指令を出している。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
jQuery ($) -> # Boids0.5のControlerを作成し、canvasオブジェクトを渡す canvas = $("#boids05_canvas")[0] controler = new Boids05.Controler(canvas) controler.setVMax(50) # Generateボタンが押されたとき、指定された個体数で群をつくる $("#boids05_generate").click -> pop = $("#boids05_population").val() if pop < 1 pop = 1 $("#boids05_population").val(pop) controler.generate(pop) |
ブラウザ側からの指令と、スクリプト内の各クラスとの仲立ちを一手に引き受けるクラスで、この段階では以下の機能を提供する。
Controlerオブジェクトを生成する。Constructorオブジェクトを生成する。Constructorオブジェクトにセットする。|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
class Controler constructor: (canvas) -> @vMax = 0 @field = new Field(canvas) @cluster = new Cluster(canvas) @population = 0 # number of creatures # 個体の速度を発生させるときの最大値 setVMax: (@vMax) -> # 一つの個体を発生させるメソッド # 位置はcanvasに収まるよう、速度はvMax/2~vMaxの範囲でランダム createCreature: -> cr = new Creature(@field) x = Math.floor(Math.random() * @field.xMax) y = Math.floor(Math.random() * @field.yMax) v = (Math.random() + 1) * @vMax / 2 a = Math.random() * Math.PI * 2 cr.setPosition(x, y) cr.setVelocity(v * Math.cos(a), v * Math.sin(a)) return cr # 指定した数の個体を発生させ、Clusterオブジェクトに登録する generate: (@population) -> @cluster.clearCreatures() for i in [1..@population] cr = @createCreature() @cluster.addCreature(cr) @cluster.draw() |
将来の拡張も考慮して、一つのクラスとした。現時点では単なる矩形で、上下左右の座標値をプロパティに持つ。
|
1 2 3 4 5 6 |
class Field constructor: (canvas) -> @xMin = 0 @yMin = 0 @xMax = canvas.width @yMax = canvas.height |
Creatureオブジェクトを1~複数保持する「群」のクラス。提供する機能は以下の通り。
canvasを渡してClusterオブジェクトを生成。Creatureオブジェクトを渡し、群に追加する。draw()メソッドを呼び出しているだけ。|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class Cluster constructor: (canvas) -> @creatures = [] @canvas = canvas @context = @canvas.getContext("2d") if @canvas.getContext return # 群の個体をすべてクリアする clearCreatures: -> @creatures = [] # 群に与えられた個体を加える addCreature: (creature) -> @creatures.push(creature) return # 群の善個体を描画する draw: -> @context.fillStyle = "#e0e0e0" @context.fillRect(0, 0, @canvas.width, @canvas.height) for creature in @creatures creature.draw(@context) return |
個々のクラスを表現するクラス。このバージョンでは運動はさせないが、速度関係のプロパティや初期化は行っている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class Creature # 描画の基本となるサイズ # private staticなクラス・プロパティ _drawSize = 4 constructor: (field) -> @x = 0 @y = 0 @vx = 0 @vy = 0 @field = field # 個体の位置をセットするメソッド setPosition: (@x, @y) -> # 個体の速度をセットするメソッド setVelocity: (@vx, @vy) -> # 個体を描画するメソッド # canvasのコンテキストを引数で受け取る draw: (ctx) -> ctx.fillStyle = "black" ctx.beginPath() ctx.arc(@x, @y, _drawSize, 0, Math.PI*2, true) ctx.fill() return |
Boids 1.0用のボックスやボタンを用意し、外部スクリプトファイルを読み込んでいる。
このバージョンから個体の運動をさせるので、Start/Stopボタンを追加している。
|
1 2 3 4 5 6 7 8 9 10 11 |
<input type="number" id="boids10_population" value="1" min="1" /><br /> <input type="button" id="boids10_generate" value="Generate" /> <input type="button" id="boids10_start_and_stop" value="Start/Stop" /> <canvas id="boids10_canvas" width="400" height="300" style="background-color: #e0e0e0"> <!-- テキストモードの最後尾 --> ... <script src="../coffee/boids/boids_1_0.js" type="text/javascript">// <![CDATA[ // ]]></script> |
パッケージについては、パッケージ名やエイリアスを変更。
また、個体の運動を追加するため、以下のメソッドを追加。
Creature.move(interval_sec)Cluster.move()Controler.setIntervalSec(interva._sec)Controler.startAndStop()|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
Boids10 = {} do -> class Field constructor: (canvas) -> class Creature constructor: (field) -> setPosition: (@x, @y) -> setVelocity: (@vx, @vy) -> draw: (ctx) -> move: (interval_sec) -> class Cluster constructor: (canvas) -> clearCreatures: -> draw: -> move: (interval_sec) -> class Controler constructor: (canvas) -> setVMax: (@vMax) -> setIntervalSec: (@interval_sec) -> createCreature: -> generate: (@population) -> startAndStop: () -> Boids10.Controler = Controler jQuery ($) -> |
秒単位のフレームタイムを指定して呼び出される。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class Field ... # Boids 1.0で追加 # interval_msはアニメーションのフレームタイム # 秒単位で与えられることを想定 move: (interval_sec) -> @x += @vx * interval_sec @y += @vy * interval_sec # 壁にぶつかった場合は全反射 if @x <= @field.xMin or @x >= @field.xMax then @vx = -@vx if @y <= @field.yMin or @y >= @field.yMax then @vy = -@vy return |
秒単位のフレームタイムを指定し、群の個体の数の分だけCreature.move()メソッドを呼び出す。
|
1 2 3 4 5 6 7 8 |
class Cluster ... # Boids 1.0で追加 # フレームタイムを秒単位で受け取り、すべての個体を移動させる move: (interval_sec) -> for creature in @creatures creature.move(interval_sec) return |
変更内容は以下の通り。
isRunningフラグintervalタイマを保持するtimerinterval_sec
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
class Controler constructor: (canvas) -> ... # Boids 1.0で追加/アニメーション用 @isRunning = false @timer = undefined @interval_sec = 1 # animation frame interval in seconds ... # Boids 1.0で追加 # フレームタイムのセット setIntervalSec: (@interval_sec) -> ... # Boids 1.0で追加 # この関数を呼び出すたびに、アニメーションの開始と停止が切り替わる # アニメーションにはsetInterval()に以下の引数を渡している # ・アニメーション1フレームの操作 # ・ミリ秒単位の時間間隔 startAndStop: () -> if @isRunning clearInterval(@timer) @isRunning = false else @timer = setInterval => @cluster.move(@interval_sec) @cluster.draw() return , @interval_sec * 1000 @isRunning = true return |
このバージョンでは、個体を壁にぶつかってから全反射させるのではなく、壁が近づくとともに斥力を感じるように壁を避けようとする動作を導入する。
Boids 1.0用のボックスやボタンを用意し、外部スクリプトファイルを読み込んでいる。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
<input type="number" id="boids11_population" value="1" min="1" /><br /> <input type="button" id="boids11_generate" value="Generate" /> <input type="button" id="boids11_start_and_stop" value="Start/Stop" /> <canvas id="boids11_canvas" width="400" height="300" style="background-color: #e0e0e0"> </canvas> <!-- テキストモードの最後尾 --> ... <script src="../coffee/boids/boids_1_1.js" type="text/javascript">// <![CDATA[ // ]]></script> |
クラス構成は特に変わらず、パッケージ名とエイリアスを本バージョンにあったものとする。以下のバージョンでも同じ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Boids11 = {} do -> class Field class Creature class Cluster class Controler Boids11.Controler = Controler jQuery ($) -> |
このバージョンから、速度の最大値をControlerからCreatureのクラスプロパティに変更(6行目)。
また、壁の接近を認識する距離(_detectionLength)と回避加速度計算時のパラメータ(_repulsionParam)を定義。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class Creature # private staticなクラス・プロパティ # 最大速度 # Boids1.0ではControlerクラスに置いていたが、 # Boids1.1からCreatureクラスのクラスプロパティとした _vMax = 0 # 描画の基本となるサイズ _drawSize = 4 # 壁の衝突回避を認識する距離 _detectionLength = 100 # 反発力パラメータ _repulsionParam = 4 |
認識距離以内に壁に近づき始めると、壁からの斥力を想定した加速度を計算し、速度を変更。
加速度は重力加速度をイメージし、距離の2乗に反比例させた。
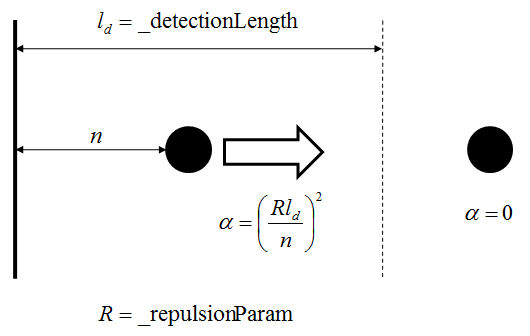
そもそもピクセル単位の計算では最小でも距離の値が”1″となるため、重力モデルでは大きな加速度が出ない。ここでは_detectionLengthを長さの基準としたが、壁との距離に応じて自然に避けるような運動をさせるためにパラメータ(_repulsionParam)を導入しなければならなかった。
なお、速度ベクトルの値のキャップを判定する際に速度成分の符号を用いているが、Math.sign()はほとんどのブラウザで使えないため、「値/絶対値」で符号を得ている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
move: (interval_sec) -> # Boids 1.1から追加 # 壁からの距離に応じた斥力を想定し、x/y方向の加速度を計算 if @x <= _detectionLength ax = (_detectionLength * _repulsionParam / @x) ** 2 else if @x >= @field.xMax - _detectionLength ax = -(_detectionLength * _repulsionParam / (@field.xMax - @x)) ** 2 else ax = 0 if @y <= _detectionLength ay = (_detectionLength * _repulsionParam / @y) ** 2 else if @y >= @field.yMax - _detectionLength ay = -(_detectionLength * _repulsionParam / (@field.yMax - @y)) ** 2 else ay = 0 # Boids 1.1から追加 # 加速度を考慮した速度の変化 # 速度の絶対値が増え続けないようにキャップで抑える # 速度成分の符号を得るのに、Math.signがサポートされていないブラウザが多いため、 # 値/絶対値で符号を得ている @vx += ax * interval_sec @vx = @vx / Math.abs(@vx) * Math.min(Math.abs(@vx), Creature._vMax) @vy += ay * interval_sec @vy = @vy / Math.abs(@vy) * Math.min(Math.abs(@vy), Creature._vMax) # インターバルの間の移動量 @x += @vx * interval_sec @y += @vy * interval_sec # 壁にぶつかった場合は全反射 if @x <= @field.xMin or @x >= @field.xMax then @vx = -@vx if @y <= @field.yMin or @y >= @field.yMax then @vy = -@vy return |
vMaxの変更のみ。
|
1 2 3 4 5 6 7 8 9 10 |
class Controler constructor: (canvas) -> # @vMax = 0 は削除 @field = new Field(canvas) @cluster = new Cluster(canvas) ... # 実際にはCreatureクラスのクラスプロパティにセットしている setVMax: (vMax) -> Creature._vMax = vMax ... |
このバージョンで、以下の点を変更している。
geom2d.Vectorで書き換えCreatureオブジェクトの形状を自由に設定可能にする本体のスクリプトファイルに先立って、独自クラスのパッケージファイル(taustation_geom2d.js)を読み込ませている。
HTMLのscript要素でパラメータ用のグローバル変数を定義する。これらはその後に読み込まれたスクリプトで利用される。
script要素内の変数定義はJavascriptで書くため、行末にコロン(;)をつけている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
<input type="number" id="boids12_population" value="1" min="1" /><br /> <input type="button" id="boids12_generate" value="Generate" /> <input type="button" id="boids12_start_and_stop" value="Start/Stop" /> <canvas id="boids12_canvas" width="400" height="300" style="background-color: #e0e0e0"> </canvas> <!-- テキストモードの最後尾 --> <!-- Boids 1.2用のパラメータ --> <script type="text/javascript">// <![CDATA[ V_MAX = 100; CREATURE_SIZE = 8; WALL_DETECTION_LENGTH = 100; WALL_REPULSION_PARAM = 16; INTERVAL_SEC = 0.05; // ]]></script> <script src="../lib/taustation_geom2d.js" type="text/javascript">// <![CDATA[ // ]]></script> ... <script src="../coffee/boids/boids_1_2.js" type="text/javascript">// <![CDATA[ // ]]></script> |
script要素をWordPressのテキストモードで書くと、ビジュアルモードを経由したときに//<![CDATA[~改行~//]]>が挿入される。
また、Javascriptをscript要素に直接書くと、改行が除かれて一行になってしまう。
独自クラスgeom2d.Vectorを使って、位置・速度・加速度のコーディングを見やすくした。
各オブジェクトの生成と計算時にVectorオブジェクトを生成するnew演算子が介在するが、400個体程度の計算でもパフォーマンスの問題は見られなかった。
これまではdraw()メソッドの中で直接円を描いていたが、今回はヘルパーメソッドdrawShape()を実装。
HTML内のスクリプト要素で定義されたグローバル変数を参照し、パラメータとしてクラス変数に格納。
この操作はControlerクラスに集約した。
@var: valの形式でクラス変数として定義。
|
1 2 3 4 5 6 7 8 9 |
class Creature # 最大速度 @_vMax: 100 # 描画の基本となるサイズ @_drawSize: 8 # 壁の衝突回避を認識する距離 @_wallDetectionLength: 100 # 反発力パラメータ @_wallRepulsionParam: 4 |
これまでx, y, vx, vyのように個別の座標値で扱っていたプロパティを、Vectorクラスで置き換える。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 位置、速度、加速度をプロパティとして持つ constructor: (field) -> @pos = new Vector(0, 0) @v = new Vector(0, 0) @a = new Vector(0, 0) @field = field # 個体の位置をセットするメソッド setPosition: (x, y) -> @pos.x = x @pos.y = y return # 個体の速度をセットするメソッド setVelocity: (vx, vy) -> @v.x = vx @v.y = vy return |
単純な円ではなく、方向を持った細長い三角形を描くように変更。
下図のように、基準点(x, y)から速度ベクトルの方向に頂点を、速度ベクトルと直角な報告に底辺を描く。ここで![]() で、これによって三角形の細長さが決まる。
で、これによって三角形の細長さが決まる。
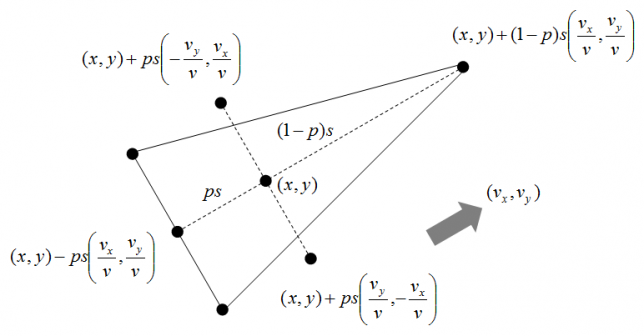
ここで![]() と置くと下図のようになる。
と置くと下図のようになる。
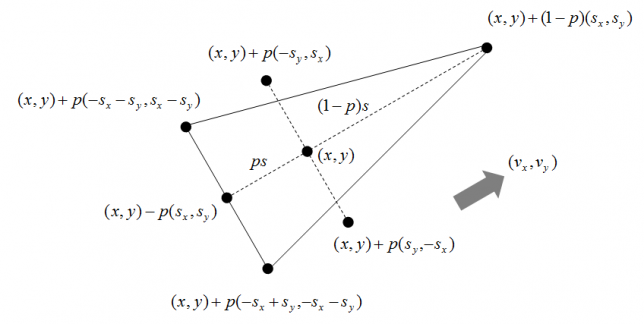
コードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 個体を描画するメソッド # canvasのコンテキストを引数で受け取る draw: (ctx) -> v = @v.abs() sx = Creature._drawSize * @v.x / v sy = Creature._drawSize * @v.y / v p = 0.25 ctx.fillStyle = "black" ctx.beginPath() ctx.moveTo(@pos.x + (1 - p) * sx, @pos.y + (1 - p) * sy) ctx.lineTo(@pos.x + (-sx - sy) * p, @pos.y + (sx - sy) * p) ctx.lineTo(@pos.x + (-sx + sy) * p, @pos.y + (-sx - sy) * p) ctx.closePath() ctx.fill() return |
Vectorオブジェクトの導入に対応して書き直した。
斥力加速度計算のパラメータ(Creature._wallRepulsionParam)は()の外に出した。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
move: (interval_sec) -> # Boids 1.1から追加 # 壁からの距離に応じた斥力を想定し、x/y方向の加速度を計算 if @pos.x <= Creature._wallDetectionLength @a.x = Creature._wallRepulsionParam * (Creature._wallDetectionLength / @pos.x) ** 2 else if @pos.x >= @field.xMax - Creature._wallDetectionLength @a.x = -Creature._wallRepulsionParam * (Creature._wallDetectionLength / (@field.xMax - @pos.x)) ** 2 else @a.x = 0 if @pos.y <= Creature._wallDetectionLength @a.y = Creature._wallRepulsionParam * (Creature._wallDetectionLength / @pos.y) ** 2 else if @pos.y >= @field.yMax - Creature._wallDetectionLength @a.y = -Creature._wallRepulsionParam * (Creature._wallDetectionLength / (@field.yMax - @pos.y)) ** 2 else @a.y = 0 # Boids 1.1から追加 # 加速度を考慮した速度の変化 # 速度の絶対値が増え続けないようにキャップで抑える @v.plusEq(@a.times interval_sec) @v.x = Math.sign(@v.x) * Math.min(Math.abs(@v.x), Creature._vMax) @v.y = Math.sign(@v.y) * Math.min(Math.abs(@v.y), Creature._vMax) # インターバルの間の移動量 @pos.plusEq(@v.times interval_sec) # 壁にぶつかった場合は全反射 if @pos.x <= @field.xMin or @pos.x >= @field.xMax then @v.x = -@v.x if @pos.y <= @field.yMin or @pos.y >= @field.yMax then @v.y = -@v.y return |
変更箇所はない。
以下のメソッド群で整理。Creatureのクラス変数をセットしている。
|
1 2 3 4 |
setVMax: (vMax) -> Creature._vMax = vMax setCreatureSize: (size) -> Creature._drawSize = size setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param |
Controlerオブジェクトのセッター群を呼び出している。
|
1 2 3 4 5 6 7 8 9 |
jQuery ($) -> canvas = $("#boids12_canvas")[0] controler = new Boids12.Controler(canvas) controler.setVMax(V_MAX) controler.setCreatureSize(CREATURE_SIZE) controler.setWallDetectionLength(WALL_DETECTION_LENGTH) controler.setWallRepulsionParam(WALL_REPULSION_PARAM) controler.setIntervalSec(INTERVAL_SEC) |
ここでは、以下のバージョンに沿って、Boidsの準備段階のコードを組み立てていく。
まずスタートアップとして、指定された数の個体を発生・表示させるという簡単な枠組みを作る。
仕様は以下の通り。
発生させた個体を表示させると同時に運動させる。
仕様は以下の通り
各個体が壁をよける動作を導入。壁からの距離に応じた斥力を想定し、それに応じた加速度を計算している。
操作方法はこれまでのものと同じ。
このバージョンでは2つのことを導入している。
操作方法はこれまでのものと同じ。