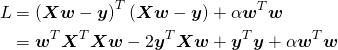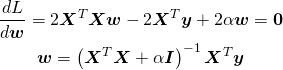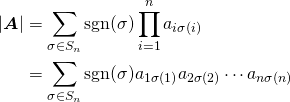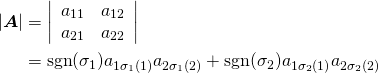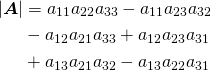scikit-learn – LinearRegression

2020-05-10 / tau / コメントする

概要

scikit-learnのLinearRegressionは、最も単純な多重線形回帰モデルを提供する。

モデルの利用方法の概要は以下の手順。

LinearRegressionのクラスをインポートする
モデルのインスタンスを生成する
fit()メソッドに訓練データを与えて学習させる

学習済みのモデルの利用方法は以下の通り。

score()メソッドにテストデータを与えて適合度を計算する
predict()メソッドに説明変数を与えてターゲットを予測
モデルインスタンスのプロパティーからモデルのパラメーターを利用
- 切片はintercept_、重み係数はcoef_(末尾のアンダースコアに注意)

利用例

配列による場合

以下はscikit-learnのBoston hose pricesデータのうち、2つの特徴量RM(1戸あたり部屋数)とLSTAT(下位層の人口比率)を取り出して、線形回帰のモデルを適用している。

特徴量の一部をとりだすのに、ファンシー・インデックスでリストの要素に2つの変数のインデックスを指定している。また、特徴量データXとターゲットデータyをtrain_test_split()を使って訓練データとテストデータに分けている。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

ds = load_boston()

X = ds.data[:, [5, 12]]
y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))
print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343
# Prediction for (7, 5):[31.14766768]
# Intercept:-0.6047107435077521
# Coefficients:[ 5.01785312 -0.67451869]

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

ds = load_boston()

X = ds.data[:, [5, 12]]

y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))

print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343

# Prediction for (7, 5):[31.14766768]

# Intercept:-0.6047107435077521

# Coefficients:[ 5.01785312 -0.67451869]

DataFrameによる場合

以下の例では、データセットの本体(data)をpandasのDataFrameとして構成し、2つの特徴量RMとLSTATを指定して取り出している。

import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

ds = load_boston()
df = pd.DataFrame(ds.data, columns=ds.feature_names)

X = df[['RM', 'LSTAT']]
y = ds['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))
print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343
# Prediction for (7, 5):[31.14766768]
# Intercept:-0.6047107435077521
# Coefficients:[ 5.01785312 -0.67451869]

import pandas as pd

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

ds = load_boston()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X = df[['RM', 'LSTAT']]

y = ds['target']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))

print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343

# Prediction for (7, 5):[31.14766768]

# Intercept:-0.6047107435077521

# Coefficients:[ 5.01785312 -0.67451869]

利用方法

モデルクラスのインポート

scikit-learn.linear_modelパッケージからLinearRegressionクラスをインポートする。

from sklearn.linear_model import LinearRegression

1	from sklearn.linear_model import LinearRegression

モデルのインスタンスの生成

LinearRegressionの場合、ハイパーパラメーターの指定はない。

lr = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

1	lr = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

fit_intercept: 切片を計算しない場合Falseを指定。デフォルトはTrueで切片も計算されるが、原点を通るべき場合にはFalseを指定する。
normalize: Trueを指定すると、特徴量Xが学習の前に正規化(normalize)される(平均を引いてL2ノルムで割る)。デフォルトはFalse。fit_intercept=Falseにセットされた場合は無視される。説明変数を標準化(standardize)する場合はこの引数をFalseにしてsklearn.preprocessing.StandardScalerを使う。
copy_X: Trueを指定するとXはコピーされ、Falseの場合は上書きされる。デフォルトはTrue。
n_jobs: 計算のジョブの数を指定する。デフォルトはNoneで1に相当。n_targets > 1のときのみ適用される。

モデルの学習

fit()メソッドに特徴量とターゲットの訓練データを与えてモデルに学習させる(回帰係数を決定する)。

lr.fit(X, y)

1	lr.fit(X, y)

X: 特徴量の配列。2次元配列で、各列が各々の説明変数に対応し、行数はデータ数を想定している。変数が1つで1次元配列の時はreshape(-1, 1)かスライス([:, n:n+1])を使って1列の列ベクトルに変換する必要がある。
y: ターゲットの配列で、通常は1変数で1次元配列。

3つ目の引数sample_weightは省略。

適合度の計算

score()メソッドに特徴量とターゲットを与えて適合度を計算する。

lr.score(X, y)

1	lr.score(X, y)

戻り値は適合度を示す実数で、回帰計算の決定係数R²で計算される。

(1) $\begin{equation*} R^2 = 1 - \frac{RSS}{TSS} = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \overline{y})^2} \end{equation*}$

モデルによる予測

predict()メソッドに特徴量を与えて、ターゲットの予測結果を得る。

y_pred = lr.predict(X)

1	y_pred = lr.predict(X)

ここで特徴量Xは複数のデータセットの2次元配列を想定しており、1組のデータの場合でも2次元配列とする必要がある。

y_pred = lr.pred([[x1, x2,..., xm]])

1	y_pred = lr.pred([[x1, x2,..., xm]])

また、結果は複数のデータセットに対する1次元配列で返されるため、ターゲットが1つの場合でも要素数1の1次元配列となる。

切片・係数の利用

fit()メソッドによる学習後、モデルの学習結果として切片と特徴量に対する重み係数を得ることができる。

各々モデル・インスタンスのプロパティーとして保持されており、切片はintercept_で1つの実数、重み係数はcoeff_で特徴量の数と同じ要素数の1次元配列となる(特徴量が1つの場合も要素数1の1次元配列)。

ic = lr.intercept_
cf = lr.coef_

1 2	ic = lr.intercept_ cf = lr.coef_

末尾のアンダースコアに注意。

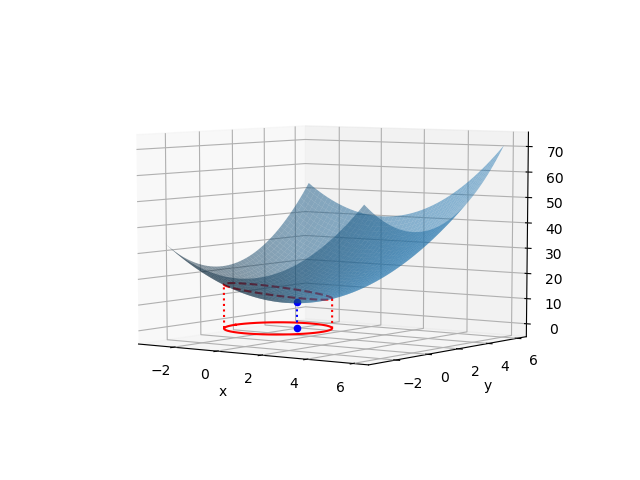
実行例

waveデータセットに対する単回帰

英語 – 機械学習

2020-05-10 / tau / コメントする

説明変数・独立変数

explately variable, regressor, independent variable, designed variable

被説明変数・従属変数: explained variable, regressand, dependent variable, designed variable

ndarray – 行・列の抽出

2020-05-09 / tau / コメントする

例示用の配列

以下の配列を例示用に準備する。

import numpy as np

a = np.arange(30).reshape(6, 5)
print(a)

# [[ 0  1  2  3  4]
#  [ 5  6  7  8  9]
#  [10 11 12 13 14]
#  [15 16 17 18 19]
#  [20 21 22 23 24]
#  [25 26 27 28 29]]

import numpy as np

a = np.arange(30).reshape(6, 5)

print(a)

# [[ 0 1 2 3 4]

# [ 5 6 7 8 9]

# [10 11 12 13 14]

# [15 16 17 18 19]

# [20 21 22 23 24]

# [25 26 27 28 29]]

単一の行・列の抽出

単一の行の抽出

単に1つ目のインデックスを指定すると、それに対応する行が抽出される。2つ目の引数を省略すると、全て':'を指定したことになる。

print(a[3])

# [15 16 17 18 19]

print(a[3])

# [15 16 17 18 19]

単一の列の抽出

1つ目の引数を':'とし、2つ目にインデックスを指定すると、対応する列が抽出される。ただし結果は1次元の配列となる。

print(a[:, 2])

# [ 2  7 12 17 22 27]

print(a[:, 2])

# [ 2 7 12 17 22 27]

これを列ベクトルとして取り出すのに2つの方法がある。

1つ目の方法はreshape(-1, 1)とする定石。2つ目の引数1は列数1を指定し、1つ目の引数を−1にすることで、列数とサイズから適切な行数が設定される。

print(a[:, 2].reshape(-1, 1))

# [[ 2]
#  [ 7]
#  [12]
#  [17]
#  [22]
#  [27]]

print(a[:, 2].reshape(-1, 1))

# [[ 2]

# [ 7]

# [12]

# [17]

# [22]

# [27]]

2つ目の方法は、列数を指定するのに敢えて1列のスライスで指定する方法。後述するように、列をスライスで指定した場合は2次元の形状が保持されることを利用している。以下の例では、2列目から2列目までの「範囲」を指定している。

print(a[:, 2:3])

# [[ 2]
#  [ 7]
#  [12]
#  [17]
#  [22]
#  [27]]

print(a[:, 2:3])

# [[ 2]

# [ 7]

# [12]

# [17]

# [22]

# [27]]

連続する複数の行・列の抽出

連続する複数行の抽出

1つ目の引数をスライスで指定して、連続する複数行を抽出。

print(a[2:5])

# [[10 11 12 13 14]
#  [15 16 17 18 19]
#  [20 21 22 23 24]]

print(a[2:5])

# [[10 11 12 13 14]

# [15 16 17 18 19]

# [20 21 22 23 24]]

連続する複数列の抽出

2つ目の引数をスライスで指定して、連続する複数列を抽出。

print(a[:, 1:4])

# [[ 1  2  3]
#  [ 6  7  8]
#  [11 12 13]
#  [16 17 18]
#  [21 22 23]
#  [26 27 28]]

print(a[:, 1:4])

# [[ 1 2 3]

# [ 6 7 8]

# [11 12 13]

# [16 17 18]

# [21 22 23]

# [26 27 28]]

不連続な複数の行・列を抽出

不連続な複数の行を抽出

第1引数をリストで指定すると、その要素をインデックスとする複数の行が抽出される。このような指定方法のインデックスを、ファンシーインデックスと言う。

print(a[[2, 4]])

# [[10 11 12 13 14]
#  [20 21 22 23 24]]

print(a[[2, 4]])

# [[10 11 12 13 14]

# [20 21 22 23 24]]

リストの要素は昇順である必要はなく、要素順に行が取り出される。

print(a[[4, 2]])

# [[20 21 22 23 24]
#  [10 11 12 13 14]]

print(a[[4, 2]])

# [[20 21 22 23 24]

# [10 11 12 13 14]]

不連続な複数の列の抽出

1つ目の引数を':'とし、2つ目の引数をリストで指定して要素に対応する列を取り出せる。

print(a[:, [1, 3]])

# [[ 1  3]
#  [ 6  8]
#  [11 13]
#  [16 18]
#  [21 23]
#  [26 28]]

print(a[:, [1, 3]])

# [[ 1 3]

# [ 6 8]

# [11 13]

# [16 18]

# [21 23]

# [26 28]]

列についても、要素の順番は任意。

print(a[:, [3, 1]])

# [[ 3  1]
#  [ 8  6]
#  [13 11]
#  [18 16]
#  [23 21]
#  [28 26]]

print(a[:, [3, 1]])

# [[ 3 1]

# [ 8 6]

# [13 11]

# [18 16]

# [23 21]

# [28 26]]

Lasso回帰の理解

2020-05-06 / tau / コメントする

定義

Ridge回帰は単純な多重回帰の損失関数に対してL2正則化項を加え、多重共線性に対する正則化を図った。Lasso解析はこれに対してL1正則化項を加えて最小化する(正則化の意味についてはこちら)。

(1) $\begin{align*} L &= \frac{1}{2} \sum_{i=1}^n ( y_i - \hat{y}_i )^2 + \alpha (|w_1| + \cdots + |w_m|) \\ &= \frac{1}{2} \sum_i ( y_i - w_0 - w_1 x_{1i} - \cdots - w_m x_{mi} )^2 + \alpha (|w_1| + \cdots + |w_m|) \end{align*}$

L1正則化の意味

準備

L2正則化は各重み係数が全体として小さくなるように制約がかかったが、L1正則化では値がゼロとなる重み係数が発生する。このことを確認する。

係数wを求めるためには損失関数Lを最小化すればよいが、Ridge回帰とは異なりL1正則化項は通常の解析的な微分はできない。

(2) $\begin{align*} \frac{\partial L}{\partial w_k} &= - \sum_i x_{ki} ( y_i - w_0 - w_1 x_{1i} - \cdots - w_m x_{mi} ) + \alpha \frac{\partial |w_k|}{\partial w_k} \\ &= - \sum_i x_{ki}y_i + w_0 \sum_i x_{ki} + \sum_{j \ne k} w_j \sum_i x_{ji} x_{ki} + w_k \sum_i {x_{ki}}^2 + \alpha \frac{\partial |w_k|}{\partial w_k} \\ &= 0 \end{align*}$

ここで $\frac{\partial |w_k|}{\partial w_k}=|w_k|'$ と表し、左辺のw_k以外に関わる項をM_k、w_kの係数となっている2乗和をS_kkと表す。

(3) $\begin{equation*} M_k + w_k S_{kk} + \alpha |w_k|' = 0 \end{equation*}$

場合分け

ここで|w_k|’についてはw_kの符号によって以下の値をとる。

(4) $\begin{equation*} |w_k|' = \left\{ \begin{array}{rl} -1 & (w_k < 0) \\ 1 & (w_k > 0) \end{array} \end{equation*}$

これらを式(3)に適用する。まずw_k < 0に対しては

(5) $\begin{gather*} w_k < 0 \quad \rightarrow \quad M_k + w_k S_{kk} - \alpha = 0 \\ -M_k + \alpha < 0 \quad \rightarrow \quad w_k = \frac{-M_k + \alpha}{S_{kk}} \end{gather*}$

またw_k > 0に対しては、

(6) $\begin{gather*} w_k > 0 \quad \rightarrow \quad M_k + w_k S_{kk} + \alpha = 0 \\ -M_k - \alpha > 0 \quad \rightarrow \quad w_k = \frac{-M_k - \alpha}{S_{kk}} \end{gather*}$

以上をまとめると、

(7) $\begin{equation*} w_k = \left\{ \begin{array}{ll} \dfrac{-M_k - \alpha}{S_{kk}} & (M_k < -\alpha) \\ \\ \dfrac{-M_k + \alpha}{S_{kk}} & (M_k > \alpha) \\ \end{array} \right. \end{equation*}$

劣微分の導入

式(7)で−α ≤ M_k ≤ αについては得られていない。M_k → ±αについてそれぞれの側から極限を計算すると0となるのでその間も0でよさそうだが、その保証はない。

ここでこちらのサイトのおかげで”劣微分(subdifferential)”という考え方を知ることができた。|w_k|’についてw_k = 0では解析的に微分不可能だが、その両側から極限をとった微分係数の範囲の集合を微分係数とするという考え方のようだ。

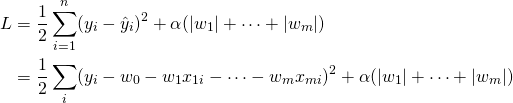
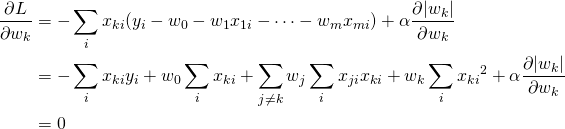
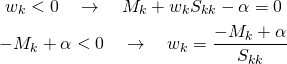
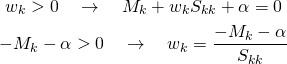
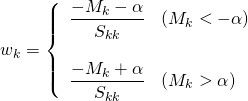
(8) $\begin{equation*} \frac{d |x|}{dx} = \left\{ \begin{array}{cl} -1 & (x < 0) \\ \left[ -1, 1 \right] & (x = 0) \\ 1 & (x > 0) \end{array} \right. \end{equation*}$

そこで、w_k = 0に対してこの劣微分を適用してみる。

(9) $\begin{gather*} w_k = 0 \quad \rightarrow \quad M_k +w_k S_{kk} + \alpha \left[ -1, 1 \right] = \left[ M_k - \alpha , M_k + \alpha \right] = 0\\ M_k - \alpha \le 0 \le M_k + \alpha \quad \rightarrow \quad -\alpha \le M_k \le \alpha \quad \rightarrow \quad w_k = 0 \end{gather*}$

以上のことから、重みw_kについて以下のようになり、−α≤M_k≤αの範囲ではw_k = 0となることがわかる。

(10) $\begin{equation*} w_k = \left\{ \begin{array}{cl} \dfrac{-M_k - \alpha}{S_{kk}} & (M_k < -\alpha \quad)\\ \\ 0 & (-\alpha \le M_k \le \alpha) \\ \\ \dfrac{-M_k + \alpha}{S_{kk}} & (M_k > \alpha) \end{array} \right. \end{equation*}$

すなわちL1正則化の場合、ハイパーパラメータαは重み係数の大きさを制限すると同時に重み係数がゼロとなるような効果も持ち、αが大きいほど多くの重み係数がゼロとなりやすい。

参考サイト

本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。

Lassoを数式から実装まで(理論編)～Miidas Research

正則化の意味～制約条件付最適化

2020-05-05 / tau / コメントする

疑　問

L2ノルムによるRidge回帰やL1ノルムによるLasso回帰に登場する罰則項。Lpノルムで表現すると次のようになる。

(1) $\begin{equation*} L(\boldsymbol{w}) = E(\boldsymbol{w}) + \alpha \sum_i |w_i|^p \end{equation*}$

ここでEは正則化がない場合の下の損失関数、w=(w₁, … , w_m)は特徴量に対する重みでLは正則化考慮後の損失関数。

このLを最小となるようなwを計算していくことになるのだが、多くの文献やサイトでL1正則化やL2正則化を説明するのに次のような図を使って、制約条件付きの最小化問題としている。

確かに式(1)の形はLagrrangeの未定乗数法に似ているのだが、ここで分からなくなるのが、αがハイパーパラメーターとして設定される点である。未定乗数法の場合、wとαを未知数として、Lを偏微分して解いていくが、ここではαは変数としては用いられない。

考え方

まず、以下のように重みwに対する制約を設定する。

(2) $\begin{equation*} \sum_i |w_i|^p \le \frac{1}{\mu} \qquad (\mu > 0) \end{equation*}$

これは、重みのノルムが高々1/μであることを意味している。これを0以下の制約条件として以下のように変形する。

(3) $\begin{equation*} g(\boldsymbol{w}) = \mu \sum_i |w_i|^p - 1 \le 0 \end{equation*}$

一般化すると $a\sum |w_i|^p + b$ の形になるが、不等式の両辺をaで割ることで、このような表現とすることは差し支えない。

これを制約条件として、元々の損失関数E(w)を最小化するため、λを導入して不等式制約条件付きのLagrangeの未定乗数法の問題を立てる。

(4) $\begin{align*} &\mathrm{minimize} \quad E(\boldsymbol{w}) \\ &\mathrm{subject~to} \quad g(\boldsymbol{w}) = \mu \sum_i |w_i|^p - 1 \le 0 \\ &\rightarrow \quad M(\boldsymbol{w}, \lambda) = E(\boldsymbol{w}) - \lambda \left( \mu \sum_i |w_i|^p - 1 \right) \end{align*}$

ここでKKT条件からλ ≤ 0となるので、ξ = −λ ≥ 0を導入して、以下のように表す。

(5) $\begin{align*} M(\boldsymbol{w}, \lambda) = E(\boldsymbol{w}) + \xi \left( \mu \sum_i |w_i|^p - 1 \right) \end{align*}$

以降、冒頭の正則化の式と上記の最小化問題の式を並べる。

(6) $\begin{align*} &L(\boldsymbol{w}) = E(\boldsymbol{w}) + \alpha \sum_i |w_i|^p \\ &M(\boldsymbol{w}, \xi) = E(\boldsymbol{w}) + \xi \left( \mu \sum_i |w_i|^p - 1 \right) \end{align*}$

これらをw_iで偏微分する。

(7) $\begin{align*} &\frac{\partial L}{\partial w_i} = \frac{\partial E}{\partial w_i} + \alpha \frac{d |w_i|^p}{d w_i} \\ &\frac{\partial M}{\partial w_i} = \frac{\partial E}{\partial w_i} + \xi \mu \frac{d |w_i|^p}{d w_i} \end{align*}$

上式から、wに関しては2つの問題は等価と言える。しかしながら、Lの最小化についてはwの解が求まるのに対して、Mの最小化で解を確定するためには、ξを未知数としてこれについても偏微分をとり、未知数と方程式を1つ加えなければならない。どうしてLの最小化だけで最適解が定まるのか。

解　釈

ところで、αはハイパーパラメーターとして外部で設定するのであった。Lに関してはw_iの個数分の未知数と方程式となり、wの解が確定する。すなわち、元の正則化の式を解くだけで「最適化された」係数のセットがw空間において1つに定まる。

ここからがミソで、wが求められるとこれを満たす制約条件の境界が定まり、同時に|w|^pに対する制約も定まるというのがどうもこの計算の仕組みらしい。

そこで、αを設定した後のながれを追ってみる。

αを設定してLを最適化する
w = (w₁, … , w_m)が定まる
点wを通る制約条件の境界g(w) = 0が定まる → Σ|w_i|^p = μ⁻¹

すなわち、αを設定してLを最適化することで制約条件の境界g = 0が決定され、重みに対する制約の強さμも決まることになる。

なお、α = 0として罰則項の効果をなくす場合のほかは必ず制約条件の境界上で解を求めることになる。一般的なLagrangeの未定乗数法のように、与えられた制約条件と目的関数の関係によって純粋な極値問題となるということはない(後述する∇Eと∇gのgradientの向きの関係からも確認できる)。

ξやμはどのように定まるのか

本来なら生真面目に未定乗数法を解いて求めるはずのξはどこへ行ったのか。

式(7)のノルム項の比較よりα = ξμ
αは事前に設定した値で、μはLの計算結果から導出されることから、ξ = μ/αも計算可能
なおMについて、点wにおいては∇E = −ξμ∇gが成り立っており、この点でEとgのgradientが平行(−ξμの符号から、両ベクトルは逆向き)

すなわち、ξはμと組み合わさって、境界条件における目的関数Eと制約条件gのgradientの比となっている。

μについては、α = ξμの関係から、αを大きくするとμも大きくなる傾向になりそうである。それにつれて式(2)から重みをより小さく制約する方向に効きそうである。ただしこの場合、ξも変動するので単純な比例関係にはならず、αの値を試行錯誤で変化させて学習効果を確認することになる。

参考サイト

本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。

過学習を防ぐ「正則化」とは？～○×（まるぺけ）つくろーどっとコム

ラグランジュの未定乗数法～不等式制約条件

2020-05-05 / tau / コメントする

概要

不等式制約条件を持つLagrangeの未定乗数法は以下のように表示される(等式条件の場合はこちらを参照)。

(1) $\begin{align*} & \mathrm{maximize/minimize} \quad f(\boldsymbol{x}) \\ & \mathrm{subject~to} \quad g(\boldsymbol{x}) \le 0 \end{align*}$

この場合、停留点が制約条件の範囲外にあれば等式条件と同じ問題となり、範囲内にあれば制約条件なしの通常の極値問題となる。

例題

停留点が制約条件の範囲内の場合

停留点が制約条件の境界内にある次のような問題を考える。

(2) $\begin{align*} & \mathrm{minimize} \quad f(x, y) = \left(x - \frac{1}{2} \right)^2 + \left(y - \frac{1}{2} \right)^2 +10 \\ & \mathrm{subject~to} \quad g(x, y) =x^2 + y^2 - 4\le 0 \\ &L(x, y, \lambda) = (x - 1)^2 + (y - 1)^2 + 10 - \lambda (x^2 + y^2 - 4) \end{align*}$

この問題を解くのに、まず停留点が制約条件の範囲内にあるかをチェックする。上の式で $\lambda=0$ と置いて最適化問題を解く。

(3) $\begin{gather*} \frac{\partial f}{\partial x} = 2\left(x - \frac{1}{2} \right) = 0 \\ \frac{\partial f}{\partial y} = 2\left(y - \frac{1}{2} \right) = 0 \\ \Downarrow \\ x = y = \frac{1}{2} \end{gather*}$

上記の解は制約条件 $g(x, y) \le 0$ を満足する。この停留点が極値だということが分かっていれば、これが問題の解ということになる。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def f(x, y, a, b):
    return (x - a)**2 + (y - b)**2 + 10

a, b = 1/2, 1/2
x = np.linspace(-3, 6)
y = np.linspace(-3, 6)
x, y = np.meshgrid(x, y)

t = np.linspace(-np.pi, np.pi)
xg = 2 * np.cos(t)
yg = 2 * np.sin(t)

x4min = 6 / np.sqrt(13)
y4min = 4 / np.sqrt(13)
fmin = f(x4min, y4min, a, b)
x4max = - 6 / np.sqrt(13)
y4max = - 4 / np.sqrt(13)
fmax = f(x4max, y4max, a, b)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(x, y, f(x, y, a, b), alpha=0.5)
ax.plot(xg, yg, 0, c='r')
ax.plot(xg, yg, f(xg, yg, a, b), c='r', linestyle='dashed')

ax.scatter(a, b, 10, c='b')
ax.scatter(a, b, 0, c='b')
ax.plot([a, a], [b, b], [0, 10], c='b', linestyle='dotted')

ax.plot([x4min, x4min], [y4min, y4min], [0, fmin], c='r', linestyle='dotted')
ax.plot([x4max, x4max], [y4max, y4max], [0, fmax], c='r', linestyle='dotted')

ax.set_xlabel("x")
ax.set_ylabel("y")

print("f_max={:8.4f}, for x={:7.4f}, y={:7.4f}".format(fmax, x4max, y4max))
print("f_min={:8.4f}, for x={:7.4f}, y={:7.4f}".format(fmin, x4min, y4min))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

def f(x, y, a, b):

return (x - a)**2 + (y - b)**2 + 10

a, b = 1/2, 1/2

x = np.linspace(-3, 6)

y = np.linspace(-3, 6)

x, y = np.meshgrid(x, y)

t = np.linspace(-np.pi, np.pi)

xg = 2 * np.cos(t)

yg = 2 * np.sin(t)

x4min = 6 / np.sqrt(13)

y4min = 4 / np.sqrt(13)

fmin = f(x4min, y4min, a, b)

x4max = - 6 / np.sqrt(13)

y4max = - 4 / np.sqrt(13)

fmax = f(x4max, y4max, a, b)

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(x, y, f(x, y, a, b), alpha=0.5)

ax.plot(xg, yg, 0, c='r')

ax.plot(xg, yg, f(xg, yg, a, b), c='r', linestyle='dashed')

ax.scatter(a, b, 10, c='b')

ax.scatter(a, b, 0, c='b')

ax.plot([a, a], [b, b], [0, 10], c='b', linestyle='dotted')

ax.plot([x4min, x4min], [y4min, y4min], [0, fmin], c='r', linestyle='dotted')

ax.plot([x4max, x4max], [y4max, y4max], [0, fmax], c='r', linestyle='dotted')

ax.set_xlabel("x")

ax.set_ylabel("y")

print("f_max={:8.4f}, for x={:7.4f}, y={:7.4f}".format(fmax, x4max, y4max))

print("f_min={:8.4f}, for x={:7.4f}, y={:7.4f}".format(fmin, x4min, y4min))

plt.show()

停留点が制約条件の範囲外の場合

今度は目的関数の停留点が制約条件の境界の範囲外にある問題を考えてみる。

(4) $\begin{align*} & \mathrm{minimize} \quad f(x, y) = (x - 3)^2 + (y-2)^2 +10 \\ & \mathrm{subject~to} \quad g(x, y) =x^2 + y^2 - 4\le 0 \\ &L(x, y, \lambda) = (x - 3)^2 + (y - 2)^2 + 10 - \lambda (x^2 + y^2 - 4) \end{align*}$

まず停留点が境界条件の範囲内にあるとして、 $\lambda = 0$ として問題を解いてみる。

(5) $\begin{gather*} \frac{\partial f}{\partial x} = 2(x - 3) = 0 \\ \frac{\partial f}{\partial y} = 2(y - 2) = 0 \\ \Downarrow \\ x = 3 , \; y = 2 \end{gather*}$

ところがこの解は制約条件 $g(x, y) \le 0$ を満足しない。解は制約条件の境界上にあることになるので、 $\lambda \ne 0$ の条件でLagrangeの未定乗数法によって解く。

(6) $\begin{gather*} \left\{ \begin{array}{c} \dfrac{\partial L}{\partial x} = 2(x - 3) - 2\lambda x = 0\\ \\ \dfrac{\partial L}{\partial y} = 2(y - 2) - 2\lambda y = 0\\ \\ \dfrac{\partial L}{\partial \lambda} = -(x^2 + y^2 - 4) = 0 \end{array} \right. \quad \Rightarrow \quad \left\{ \begin{array}{c} (1 - \lambda) x = 3\\ (1 - \lambda) y = 2\\ x^2 + y^2 = 4 \end{array} \right. \end{gather*}$

$\lambda \ne 1$ として、

(7) $\begin{gather*} x = \frac{3}{1 - \lambda} , \; y = \frac{2}{1 - \lambda} , \; 1 - \lambda = \pm \frac{\sqrt{13}}{2} \\ \left\{ \begin{array}{rll} \lambda &= 1 \mp \dfrac{\sqrt{13}}{2} & \fallingdotseq -0.8028 , \; 2.8028 \\ x &= \pm \dfrac{6}{\sqrt{13}} & \fallingdotseq 1.6641 , \; -1.6641 \\ y &= \pm \dfrac{4}{\sqrt{13}} & \fallingdotseq 1.1094 , \; -1.1094 \\ f(x, y) &= 17 \pm \dfrac{52}{\sqrt{13}} & \fallingdotseq 12.5778 , \; 41.4222 \end{array} \right. \end{gather*}$

いずれの解も制約条件 $g(x, y)=0$ を満たしており、このうち最小値となる解と目的関数の値は以下の通り。

(8) $\begin{gather*} (x, y, f(x, y)) = \left( \frac{6}{\sqrt{13}} , \frac{4}{\sqrt{13}} , 17 - \dfrac{52}{\sqrt{13}} \right) \fallingdotseq (1,6641, 1.1094, 12.5778) \end{gather*}$

λの符号について

有界でない例

以下、制約条件が $g(x, y) \le 0$ で有界でない場合を考える。

最小化問題でgradientが逆向き(極値が制約条件外)

まず、目的関数を最小化する場合を考える。以下の問題では目的関数fの極値が制約条件の範囲外にあり、fとgのgradientがgの境界上で逆向きになる。

(9) $\begin{align*} &\mathrm{minimize} \quad f(x, y) = (x - 1)^2 + (y - 1)^2 \\ &\mathrm{subject~to} \quad g(x, y) = x + y \le 0 \\ &L(x, y, z) = (x - 1)^2 + (y - 1)^2 - \lambda(x + y) \end{align*}$

停留点は制約条件の境界上となることから、λ≠0として未定乗数法で解いて以下を得る。λ<0となり、gradientが逆向きであることが現れている(∇f = λ∇g)。

(10) $\begin{equation*} x = 0, \; y = 0, \; \lambda = -2 \end{equation*}$

最小化問題でgradientが同じ向き(極値が制約条件内)

次の問題では極値が制約条件の範囲内にあり、fとgのgradientがgの境界上で同じ向きとなる。

(11) $\begin{align*} &\mathrm{minimize} \quad f(x, y) = (x + 1)^2 + (y + 1)^2 \\ &\mathrm{subject~to} \quad g(x, y) = x + y \le 0 \\ &L(x, y, z) = (x + 1)^2 + (y + 1)^2 - \lambda(x + y) \end{align*}$

この場合、fの極値は制約条件(緑色)の範囲内にあり、fとgのgradientがgの境界上で同じ向きになる。停留点は制約条件内にあることから、λ=0として制約条件の効果をなくし、単純にfの極値問題を解いて以下を得る(∇f =0)。

(12) $\begin{equation*} x = -1, \; y = -1, \; \lambda = 0 \end{equation*}$

最大化問題でgradientが同じ向き(極値が制約条件範囲外)

次に目的関数を最大化する場合を考える。以下の問題では目的関数fの極値が制約条件の範囲外にあり、fとgのgradientがgの境界上で同じ向きになる。

(13) $\begin{align*} &\mathrm{minimize} \quad f(x, y) = - (x - 1)^2 - (y - 1)^2 \\ &\mathrm{subject~to} \quad g(x, y) = x + y \le 0 \\ &L(x, y, z) = - (x - 1)^2 - (y - 1)^2 - \lambda(x + y) \end{align*}$

停留点は制約条件の境界上となることから、λ≠0として未定乗数法で解いて以下を得る。λ>0となり、gradientが同じ向きであることが現れている(∇f = λ∇g)。

(14) $\begin{equation*} x = 0, \; y = 0, \; \lambda = 2 \end{equation*}$

最大化問題でgradientが逆向き(極値が制約条件範囲内)

次の問題では極値が制約条件の範囲内にあり、fとgのgradientがgの境界上で逆向きとなる。

(15) $\begin{align*} &\mathrm{minimize} \quad f(x, y) = - (x + 1)^2 - (y + 1)^2 \\ &\mathrm{subject~to} \quad g(x, y) = x + y \le 0 \\ &L(x, y, z) = - (x + 1)^2 - (y + 1)^2 - \lambda(x + y) \end{align*}$

この場合、fの極値は制約条件(緑色)の範囲内にあり、fとgのgradientがgの境界上で逆向きになる。停留点は制約条件内にあることから、λ=0として制約条件の効果をなくし、単純にfの極値問題を解いて以下を得る(∇f =0)。

(16) $\begin{equation*} x = -1, \; y = -1, \; \lambda = 0 \end{equation*}$

λの符号について

以上の4つのパターンをまとめると、以下のようになる。

	∇fと∇gが同方向	∇fと∇gが逆方向
fを最小化	制約条件内 λ = 0, g(x, y) < 0	制約条件外(境界上) λ < 0, g(x, y) = 0
fを最大化	制約条件外(境界上) λ > 0, g(x, y) = 0	制約条件内 λ = 0, g(x, y) < 0

たとえばfを最大化する場合の条件をまとめて書くと、

(17) $\begin{equation*} g(x, y) \le 0 , \quad \lambda \ge 0 , \quad \lambda g(x, y) = 0 \end{equation*}$

これがKKT条件と呼ばれるもの。

ただし上記の場合分けは、最小化問題か最大化問題かによってλの符号が異なっている。さらに未定乗数を求める関数をここではL = f − λgとしたが、L = f + λgとしている場合もあり、このときはまたλの不等号が逆になってややこしい。

KKT条件では、一般にλ ≥ 0とされるが、元の問題が最小化か最大化か、不等式制約条件を正とするか負とするか、未定乗数法の関数形がf − λgかf + λgか、設定条件によってこの符号が反転する。逆に言えば、もともとのKKT条件がλ ≥ 0と示されているので、最小化(あるいは最大化)に対して−∇gとしたり、L = f ± gを使い分けたり、g ⋚ 0の設定を選んだりしている節がある。

KKT条件

不等式制約条件付きの最適化問題において、Lagrangeの未定乗数法を適用する場合の条件は、一般にKKT条件(Karush-Kuhn-Tucker condition)として示されるが、問題設定の形式を明示する必要がある(あるいは最小化問題と最大化問題でλの不等号を反転させた形で示す)。

最大化問題を基本とし、不等式制約条件は0又は負とする。ラグランジュ関数の制約条件項の符号はマイナスとする。

(18) $\begin{align*} &\mathrm{maximize} \quad f(\boldsymbol{x}) \\ &\mathrm{subject~to} \quad g(\boldsymbol{x}) \le 0 \\ &\rightarrow \; \mathrm{maximize} \quad L(\boldsymbol{x}, \lambda) = f(\boldsymbol{x}) - \lambda g(\boldsymbols{x}) \end{align*}$

この時、ラグランジュ関数を最大化するKKT条件は

(19) $\begin{gather*} g(x, y) \le 0 \\ \lambda \ge 0\\ \lambda g(x, y) = 0 \end{gather*}$

最小化問題の場合には、最大化問題となるように目的関数を反転する。

(20) $\begin{align*} &\mathrm{minimize} \quad f(\boldsymbol{x}) \\ &\mathrm{subject~to} \quad g(\boldsymbol{x}) \le 0 \\ &\rightarrow \; \mathrm{maximize} \quad L(\boldsymbol{x}, \lambda) = - f(\boldsymbol{x}) - \lambda g(\boldsymbols{x}) \end{align*}$

あるいは元のままの関数形として、最小化問題とKKT条件を以下のように設定してもよい。

(21) $\begin{gather*} \mathrm{minimize} \quad L(\boldsymbol{x}, \lambda) = f(\boldsymbol{x}) - \lambda g(\boldsymbols{x}) \\ g(x, y) \le 0 \\ \lambda \le 0\\ \lambda g(x, y) = 0 \end{gather*}$

参考サイト

本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。

matplotlib.patches – 図形の描画

2020-04-30 / tau / コメントする

概要

matplotlib.patchesパッケージに様々な図形クラスが準備されていて、Axesのadd_patch()メソッドでそれらのオブジェクトを加えていく。

import matplotlib.pyplot as plt
import matplotlib.patches as patch

fig, ax = plt.subplots()

circ = patch.Circle(xy=(3, 3), radius=2, ec='b', fc='gray')
elli = patch.Ellipse(xy=(2, 1), width=2, height=1, ec='g', fill=False, angle=10)
rect = patch.Rectangle(xy=(1, 2), width=3, height=2, ec='b', fc='w', angle=30)

ax.add_patch(circ)
ax.add_patch(elli)
ax.add_patch(rect)

ax.set_xlim(0, 6)
ax.set_ylim(0, 6)
ax.set_aspect('equal')

plt.show()

import matplotlib.pyplot as plt

import matplotlib.patches as patch

fig, ax = plt.subplots()

circ = patch.Circle(xy=(3, 3), radius=2, ec='b', fc='gray')

elli = patch.Ellipse(xy=(2, 1), width=2, height=1, ec='g', fill=False, angle=10)

rect = patch.Rectangle(xy=(1, 2), width=3, height=2, ec='b', fc='w', angle=30)

ax.add_patch(circ)

ax.add_patch(elli)

ax.add_patch(rect)

ax.set_xlim(0, 6)

ax.set_ylim(0, 6)

ax.set_aspect('equal')

plt.show()

各種図形

以下の点は各図形において共通

ほとんどの図形は引数xyで基準点のx座標とy座標をタプルで与える
edgecolor/ecで外枠の色、facecolor/fcで塗りつぶし色を指定する
fill=True/Falseで塗りつぶしの有無を指定する
angleで傾きの角度を指定できる図形がある

Circle(xy[, radius=5]): 中心点を指定して円を描く。
Ellipse(xy, width, height[, angle]): 中心点と幅・高さを指定して楕円を描く。
Rectangle(xy, width, height[, angle]): 左下の点と幅・高さを指定して楕円を描く。
CirclePolygon(x, y, rasius=5, resolution=20): 多角形を描画。辺／頂点の数をresolutionで指定する。
Polygon(xy, closed=True): 複数の点を指定して図形を描画する。xyはNx2配列(xy座標を要素とした2次元配列)。closedをFalseに指定すると図形の最初の点と最後の点を結ばない。
Arc(xy, width, height[, angle, theta1, theta2]): 楕円の一部の弧を描く。扇形に中を塗りつぶすことはできない。
Wedge(center, r, theta1, theta2[, width=None]): 円の一部を切出した図形を描く。widhを指定すると中心からその長さだけ除かれて描かれる。

Arrow(x, y, dx, dy[, width, ...]): 矢印を描画する。
FancyArrow(x, y, dx, dy[, width, ...]): 鏃を片側だけにしたり、鏃の大きさや形を設定したりできる。

arg max

2020-04-29 / tau / コメントする

maxが関数の最大値を意味するのに対して、arg maxは関数が最大値をとる場合の定義域を意味する。

(1) $\begin{align*} &\max x(4-x) = 4\\ &\arg \max x(4-x) = 2 \end{align*}$

定義域を指定する場合。

(2) $\begin{align*} &{\arg \max}_{-1 \le x \le 0} \, x(x + 1)(x - 1) = -\frac{1}{\sqrt{3}}\\ &\max_{-1 \le x \le 0} x(x + 1)(x - 1) = \frac{2\sqrt{3}}{9} \end{align*}$

本来arg maxは関数が最大値をとる定義域の集合を表す。

(3) $\begin{equation*} {\arg \max}_{0 \le x \le 4\pi} \, \cos x = \{ 0, 2\pi, 4\pi\} \end{equation*}$

Ridge回帰の理解

2020-04-26 / tau / コメントする

定義

Ridge回帰は多重回帰の損失関数に罰則項としてL2正則化項を加味する。正則化の意味についてはこちらに詳しくまとめている。

L2ノルムは原点からのユークリッド距離。

(1) $\begin{equation*} \| \boldsymbol{w} \| _2 = \sqrt{w_1 ^2 + \cdots + w_m^2} \end{equation*}$

ただしリッジ回帰では、根号の中の二乗項で計算する。

(2) $\begin{equation*} \mathrm{minimize} \quad \sum_{i=1}^n (y_i - \hat{y}_i) + \alpha \sum_{j=1}^m w_j^2 \end{equation*}$

定式化

最小化すべき関数は、

(3) $\begin{align*} L &= \sum_{i=1}^n ( \hat{y}_i - y_i )^2 + \alpha ({w_1}^2 + \cdots + {w_2}^2) \\ &= \sum ( w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i )^2 + \alpha ({w_1}^2 + \cdots + {w_m}^2) \end{align*}$

重み係数を計算するために、それぞれで偏微分してゼロとする。

(4) $\begin{align*} \frac{\partial L}{\partial w_0} &= 2 \sum (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) = 0 \\ \frac{\partial L}{\partial w_1} &= 2 \sum x_{1i} (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) + 2 \alpha w_1 = 0 \\ \vdots\\ \frac{\partial L}{\partial w_m} &= 2 \sum x_{mi} (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) + 2 \alpha w_m = 0\\ \end{align*}$

その結果得られる連立方程式は以下の通り。

(5) $\begin{align*} n w_0 + w_1 \sum x_{1i} + \cdots + w_m \sum x_{mi} &= \sum y_i \\ w_0 \sum x_{1i} + w_1 \left( \sum {x_{1i}}^2 + \alpha \right) + \cdots + w_m \sum x_{1i} x_{mi} &= \sum x_{1i} y_i \\ \vdots \\ w_0 \sum x_{mi} + w_1 \sum x_{1i} x_{mi} + \cdots+ w_m \left( \sum {x_{mi}}^2 + \alpha \right) &= \sum x_{mi} y_i \\ \end{align*}$

ここでそれぞれの和を記号Sと添字で表し、さらに行列表示すると以下の通り。

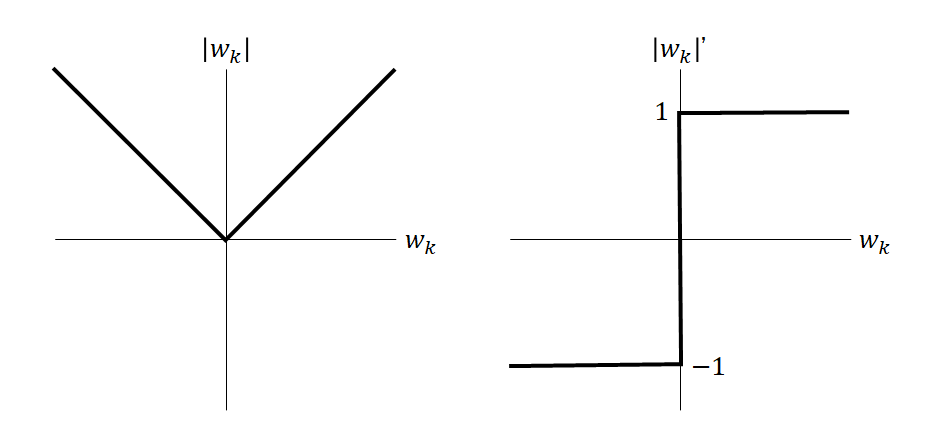
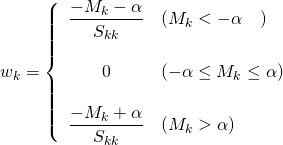
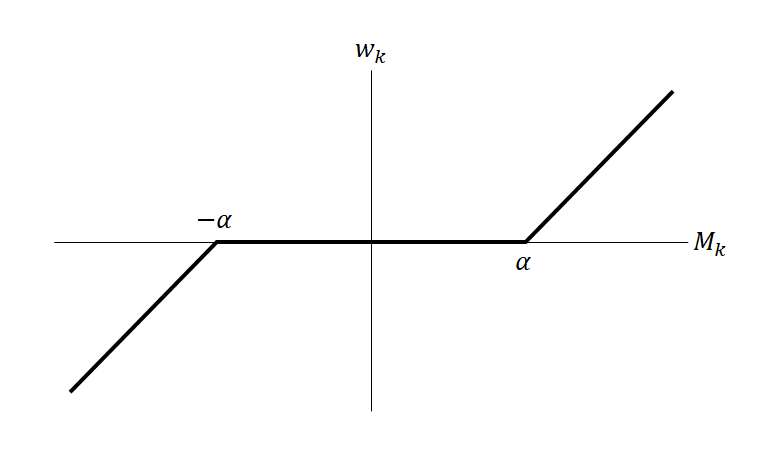
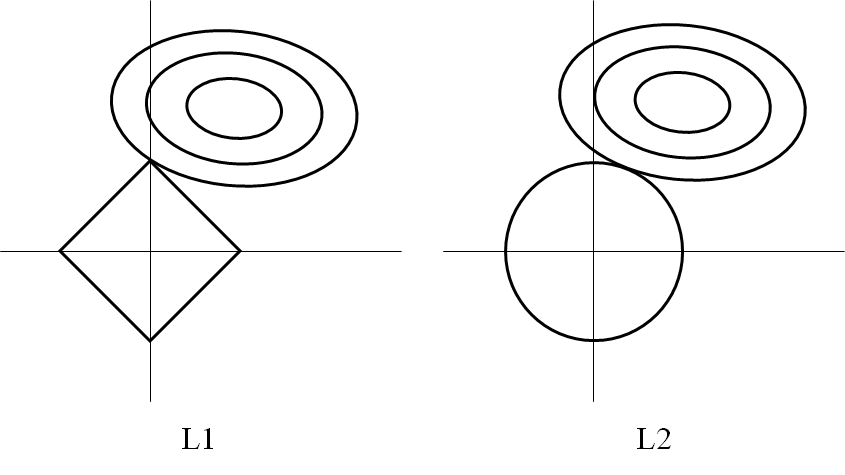
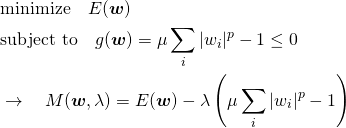
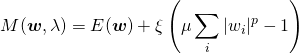
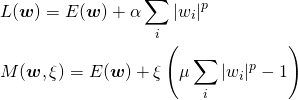
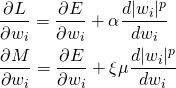
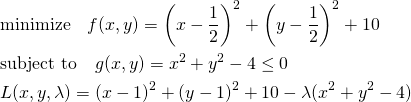
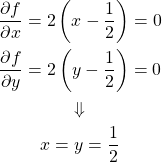
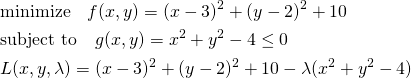
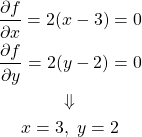
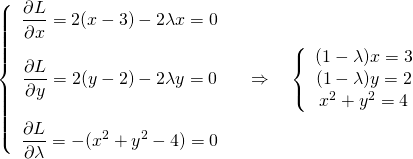
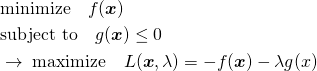
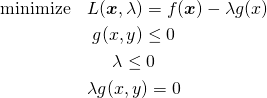
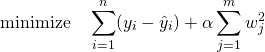
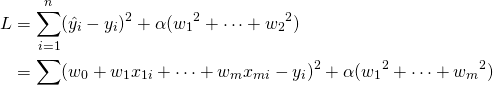
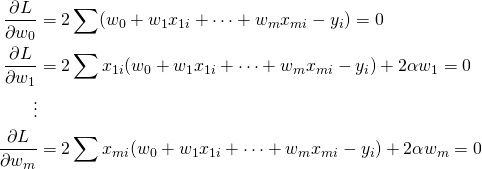
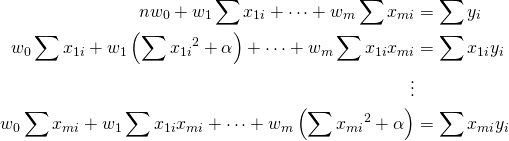
(6) $\begin{equation*} \left[ \begin{array}{cccc} n & S_1 & \cdots & S_m \\ S_1 & S_{11} + \alpha & & S_{1m} \\ \vdots & \vdots & & \vdots \\ S_m & S_{m1} & \cdots & S_{mm} + \alpha \end{array} \right] \left[ \begin{array}{c} w_0 \\ w_1 \\ \vdots \\ w_m \end{array} \right] = \left[ \begin{array}{c} S_y \\S_{1y} \\ \vdots \\ S_{my} \end{array} \right] \end{equation*}$

ここで $w_0$ を消去して、以下の連立方程式を得る。

(7) $\begin{align*} &\left[ \begin{array}{ccc} ( S_{11} + \alpha ) - \dfrac{{S_1}^2}{n} & \cdots & S_{1m} - \dfrac{S_1 S_m}{n} \\ \vdots & & \vdots \\ S_{m1} - \dfrac{S_m S_1}{n} & \cdots & ( S_{mm} + \alpha )- \dfrac{{S_2}^2}{n} \end{array} \right] \left[ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array} \right] \\&= \left[ \begin{array}{c} S_{1y} - \dfrac{S_1 S_y}{n} \\ \vdots \\ S_{my} - \dfrac{S_m S_y}{n} \end{array} \right] \end{align*}$

これを分散・共分散で表すと、

(8) $\begin{equation*} \left[ \begin{array}{ccc} V_{11} + \dfrac{\alpha}{n} & \cdots & V_{1m} \\ \vdots & & \vdots \\ V_{m1} & \cdots & V_{mm} + \dfrac{\alpha}{n} \end{array} \right] \left[ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array} \right] = \left[ \begin{array}{c} V_{1y} \\ \vdots \\ V_{my} \end{array} \right] \end{equation*}$

ここで仮に、x_jiとx_kiが完全な線形関係にある場合を考えてみる。 $x_j = a x_i + b$ とすると、分散・共分散の性質より、

(9) $\begin{equation*} V_{jj} = a^2V_{ii}, \; V_{ji} = V_{ij} = aV_{ii}, \; V_{jk} = V_{kj} = aV_{ji} = aV_{ij} \end{equation*}$

このような場合、通常の線形回帰は多重共線性により解を持たないが、式(8)に適用すると係数行列は以下のようになる。

(10) $\begin{align*} \left[ \begin{array}{ccccccc} V_{11} + \dfrac{\alpha}{n} & \cdots & V_{1i} & \cdots & aV_{1i} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} + \dfrac{\alpha}{n} & \cdots & aV_{ii} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ aV_{i1} & \cdots & aV_{ii} & \cdots & a^2V_{ii} + \dfrac{\alpha}{n} & \cdots & aV_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & aV_{mi} & \cdots & V_{mm} + \dfrac{\alpha}{n} \end{array} \right] \end{align*}$

対角要素にαが加わることで、多重共線性が強い場合でも係数行列の行列式は正則となり、方程式は解を持つ。また正則化の効果より、αを大きな値とすることによって係数の値が小さく抑えられる。

行列による表示

式(3)の損失関数を、n個のデータに対する行列で表示すると以下の通り（重回帰の行列表現はこちらを参照）。

(11) $\begin{align*} L &= \left( \boldsymbol{Xw} - \boldsymbol{y} \right)^T \left( \boldsymbol{Xw} - \boldsymbol{y} \right) + \alpha \boldsymbol{w}^T \boldsymbol{w} \\ &= \boldsymbol{w}^T \boldsymbol{X}^T \boldsymbol{Xw} - 2\boldsymbol{y}^T \boldsymbol{Xw} + \boldsymbol{y}^T \boldsymbol{y} + \alpha \boldsymbol{w}^T \boldsymbol{w} \end{align*}$

これをwで微分してLを最小とする値を求める。

(12) $\begin{gather*} \frac{dL}{d\boldsymbol{w}} = 2\boldsymbol{X}^T \boldsymbol{Xw} - 2 \boldsymbol{X}^T \boldsymbol{y} + 2 \alpha \boldsymbol{w} = \boldsymbol{0} \\ \boldsymbol{w} = \left( \boldsymbol{X}^T \boldsymbol{X} + \alpha \boldsymbol{I} \right)^{-1} \boldsymbol{X}^T \boldsymbol{y} \end{gather*}$

行列式の定義

2020-04-23 / tau / コメントする

定義式

(1) $\begin{align*} |\boldsymbol{A}| &= \sum_{\sigma \in S_n} {\rm sgn}(\sigma) \prod_{i=1}^n a_{i\sigma(i)} \\ &= \sum_{\sigma \in S_n} {\rm sgn}(\sigma) a_{1\sigma(1)} a_{2\sigma(2)} \cdots a_{n\sigma(n)} \end{align*}$

計算例

次数2の場合

(2) $\begin{align*} |\boldsymbol{A}| &= \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| \\ &= {\rm sgn}(\sigma_1)a_{1\sigma_1(1)}a_{2\sigma_1(2)} + {\rm sgn}(\sigma_2)a_{1\sigma_2(1)}a_{2\sigma_2(2)} \end{align*}$

ここで、

(3) $\begin{equation*} \sigma_1 = \left( \begin{array}{cc} 1 & 2 \\ 1 & 2 \end{array} \right) ,\quad \sigma_2 = \left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \end{array} \right) \end{equation*}$

(4) $\begin{equation*} {\rm sgn}(\sigma_1) = 1 ,\quad {\rm sgn}(\sigma_2) = -1 \end{equation*}$

(5) $\begin{equation*} \sigma_1(1) = 1 ,\; \sigma_1(2) = 2 ,\; \sigma_2(1) = 2 ,\; \sigma_2(2) = 1 \end{equation*}$

したがって行列式の値は、

(6) $\begin{equation*} |\boldsymbol{A}| = a_{11}a_{22} - a_{12}a_{21} \end{equation*}$

次数3の場合

(7) $\begin{align*} |\boldsymbol{A}| =& \left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| \\ =& {\rm sgn}(\sigma_1)a_{1\sigma_1(1)}a_{2\sigma_1(2)}a_{3\sigma_1(3)} + {\rm sgn}(\sigma_2)a_{1\sigma_2(1)}a_{2\sigma_2(2)}a_{3\sigma_2(3)}\\ &{\rm sgn}(\sigma_3)a_{1\sigma_3(1)}a_{2\sigma_3(2)}a_{3\sigma_3(3)} + {\rm sgn}(\sigma_4)a_{1\sigma_4(1)}a_{2\sigma_4(2)}a_{4\sigma_4(3)}\\ &{\rm sgn}(\sigma_5)a_{1\sigma_5(1)}a_{2\sigma_5(2)}a_{3\sigma_5(3)} + {\rm sgn}(\sigma_6)a_{1\sigma_6(1)}a_{2\sigma_6(2)}a_{4\sigma_6(3)} \end{align*}$

ここで、

(8) $\begin{gather*} \sigma_1 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \end{array} \right) ,\quad \sigma_2 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \end{array} \right) \\ \sigma_3 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \end{array} \right) ,\quad \sigma_4 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array} \right) \\ \sigma_5 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \end{array} \right) ,\quad \sigma_6 = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array} \right) \end{gather*}$

(9) $\begin{equation*} \begin{array}{ll} {\rm sgn}(\sigma_1) = \phantom{-}1 ,& {\rm sgn}(\sigma_2) = -1 \\ {\rm sgn}(\sigma_3) = -1 ,& {\rm sgn}(\sigma_4) = \phantom{-}1 \\ {\rm sgn}(\sigma_5) = \phantom{-}1 ,& {\rm sgn}(\sigma_6) = -1 \end{array} \end{equation*}$

(10) $\begin{gather*} \sigma_1(1) = 1 ,\; \sigma_1(2) = 2 ,\; \sigma_1(3) = 3 \\ \sigma_2(1) = 1 ,\; \sigma_2(2) = 3 ,\; \sigma_2(3) = 2 \\ \sigma_3(1) = 2 ,\; \sigma_3(2) = 1 ,\; \sigma_3(3) = 3 \\ \sigma_4(1) = 2 ,\; \sigma_2(2) = 3 ,\; \sigma_4(3) = 1 \\ \sigma_5(1) = 3 ,\; \sigma_5(2) = 1 ,\; \sigma_5(3) = 2 \\ \sigma_6(1) = 3 ,\; \sigma_6(2) = 2 ,\; \sigma_6(3) = 1 \end{gather*}$

したがって行列式の値は、

(11) $\begin{align*} |\boldsymbol{A}| &= a_{11}a_{22}a_{33} - a_{11}a_{23}a_{32} \\ &- a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} \\ &+ a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} \end{align*}$

概要

利用例

配列による場合

DataFrameによる場合

利用方法

モデルクラスのインポート

モデルのインスタンスの生成

モデルの学習

適合度の計算

モデルによる予測

切片・係数の利用

実行例

例示用の配列

単一の行・列の抽出

単一の行の抽出

単一の列の抽出

連続する複数の行・列の抽出

連続する複数行の抽出

連続する複数列の抽出

不連続な複数の行・列を抽出

不連続な複数の行を抽出

不連続な複数の列の抽出

定義

L1正則化の意味

準備

場合分け

劣微分の導入

参考サイト

疑 問

考え方

解 釈

ξやμはどのように定まるのか

参考サイト

概要

例題

停留点が制約条件の範囲内の場合

停留点が制約条件の範囲外の場合

λの符号について

有界でない例

最小化問題でgradientが逆向き(極値が制約条件外)

最小化問題でgradientが同じ向き(極値が制約条件内)

最大化問題でgradientが同じ向き(極値が制約条件範囲外)

最大化問題でgradientが逆向き(極値が制約条件範囲内)

λの符号について

KKT条件

参考サイト

概要

各種図形

定義

定式化

行列による表示

定義式

計算例

次数2の場合

次数3の場合

疑　問

解　釈