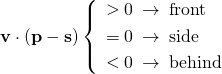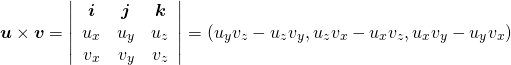直線のパラメータ表示
たとえば2次元の直線のパラメータ表示は、以下のように一つのパラメータtに対してxとyが計算される方法。
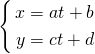
直線の決定
通過点と方向が与えられた場合
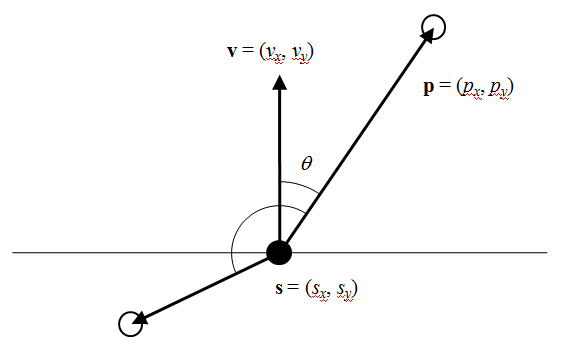
直線が通過すべき点(px, py)と、直線の方向(vx, vy)が与えられた場合のパラメータ表示を決定する。
通過点でパラメータがt = 0とすればpxとpyが定まり、tが1単位増えた時のxとyの増分が直線の方向に対応することから、以下のように表される。
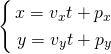
なおこれらを、パラメータtに対応した直線状の点の位置ベクトル 、通過点の位置ベクトル
、通過点の位置ベクトル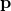 、方向ベクトル
、方向ベクトル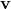 で表示すると下記のようになる。
で表示すると下記のようになる。
![Rendered by QuickLaTeX.com \[{\bf x} = {\bf v} t + {\bf p}\]](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-22c1580abd77b8da854839168a009dd3_l3.png)
2つの通過点が与えられた場合
2つの点p(px, py)とq(qx, qy)が与えられた場合の直線のパラメータ表示を決定する。
点pでt = 0、点qでt = 1とすれば、以下の式が得られる。
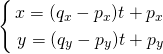
これをベクトル表示すれば以下の通り。
![Rendered by QuickLaTeX.com \[{\bf x} = ( {\bf q} - {\bf p} ) t + {\bf p}\]](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-bffc99ae09f11b5003cef976da3b7e6f_l3.png)
直線の式との関係
一般に直線の式は以下で与えられる。
![Rendered by QuickLaTeX.com \[ax + by + c = 0\]](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d6669e1ae42cc660f08ff567578c9ff2_l3.png)
一方で媒介変数された直線の式からパラメーターを消去すると以下のようになる。
![Rendered by QuickLaTeX.com \[\frac{x - p_x}{v_x} = \frac{y - p_y}{v_y}\]](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-4c6865f412510ed62db5fee6baa9ee20_l3.png)
これを変形すると、先の直線の式との対応関係がわかる。
![Rendered by QuickLaTeX.com \[v_y x - v_x y -v_x p_x + v_y p_y = 0\]](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-d6043e5cde797239480f7848c88440a2_l3.png)
交点の特定
以下の2つの直線の交点を求める。
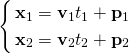
これを要素表示に展開する。
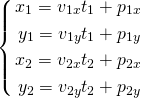
ここでx1 = x2、y1 = y2と置いて、t1、t2を未知数とした以下の方程式を得る。
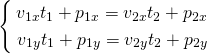
この方程式を行列で表示すると以下の通り。
![Rendered by QuickLaTeX.com \[\left[ \begin{array}{cc} v_{1x} & -v_{2x} \\ v_{1y} & -v_{2y} \end{array} \right] \left[ \begin{array}{c} t_1 \\ t_2 \end{array} \right] = \left[ \begin{array}{c} p_{2x} - p_{1x} \\ p_{2y} - p_{1y} \end{array} \right] = \left[ \begin{array}{c} \Delta p_x \\ \Delta p_y \end{array} \right]\]](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-ef97098a78b1acd2e392dd0142a0e07e_l3.png)
これを解いて以下を得る。
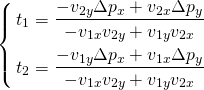
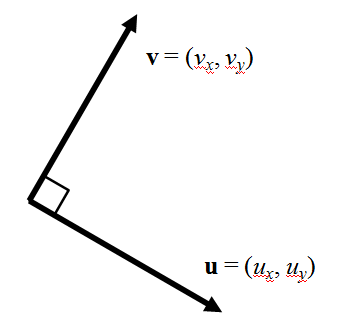
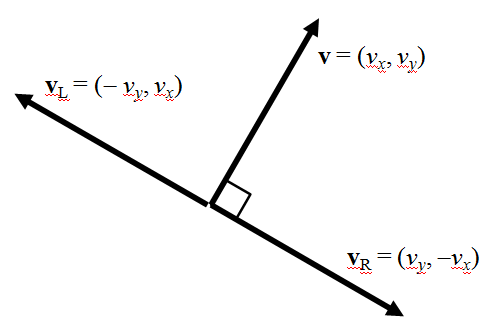
これらの式は分母がゼロのときは解をもたないが、これは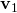 と
と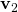 を90度回転させたベクトルが直角であること、すなわち2つの直線の方向が平行であることを示している。
を90度回転させたベクトルが直角であること、すなわち2つの直線の方向が平行であることを示している。
さらに2つの直線がまったく一致するときは、分母・分子ともゼロとなり、解は不定となる。
ここで、交点の座標を確認する。
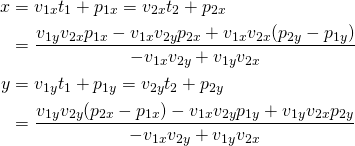
当然この結果は、パラメータ表示の2直線からパラメータt1、t2を消去して陰関数表示をした以下の方程式の解と一致する。
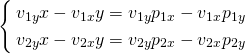
交点の位置
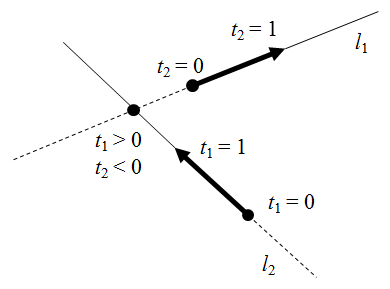
パラメータ表示の場合、基準点においてt = 0とし、方向ベクトルの先、あるいはそれに相当する2つ目の点においてt = 1などとすれば、基準点から方向ベクトルの先のtは正の値、逆方向ではtが負の値になる。
これを利用して、二つの直線の交点が基準点より前方/後方どちらの側にあるか、あるいは半直線に交点が存在するか、といった判定が容易に可能となる。
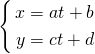
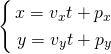
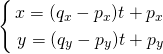
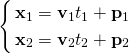
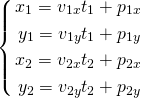
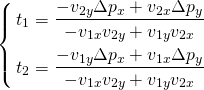
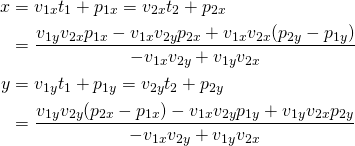
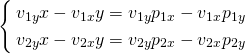

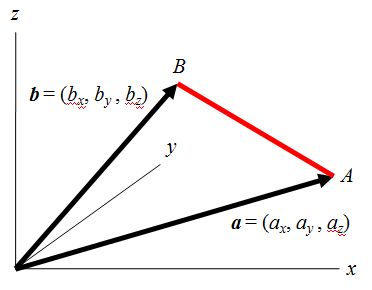
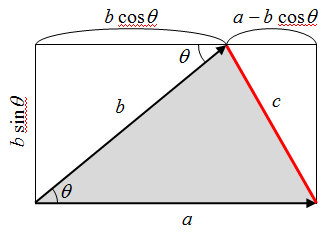
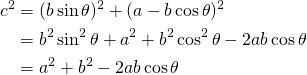
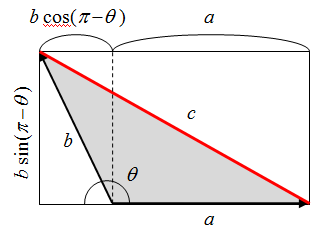
![Rendered by QuickLaTeX.com $$ \begin{align*} c^2 &= \left[ b \sin ( \pi - \theta ) \right]^2 + \left[ b \cos ( \pi - \theta ) + a \right]^2 \\ &= (b \sin \theta )^2 + (-b \cos \theta + a)^2 \\ &= b^2 \sin ^2 \theta + b^2 \cos ^2 \theta + a^2 - 2ab \cos \theta \\ &= a^2 + b^2 - 2ab \cos \theta \end{align} $$](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-bbbc758041289d3592c77d7729f346bf_l3.png)