カイ二乗分布～χ2分布

概要

独立に標準正規分布に従う確率変数X₁, …, X_kがあるとき、以下の統計量は自由度kのカイ二乗分布に従う。

(1) $\begin{equation*} Z = \sum_{i=1}^k {X_i}^2 \end{equation*}$

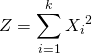
確率密度関数

x ≥ 0に対して、以下の形をとる。Γはガンマ関数。

(2) $\begin{equation*} f(x; k) = \frac{1}{2^{\frac{k}{2}} \Gamma \left(\dfrac{k}{2} \right)} x^{\frac{k}{2} - 1} e^{-\frac{x}{2}} \end{equation*}$

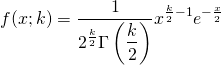
自由度kのカイ二乗分布の平均はk、分散は2k。

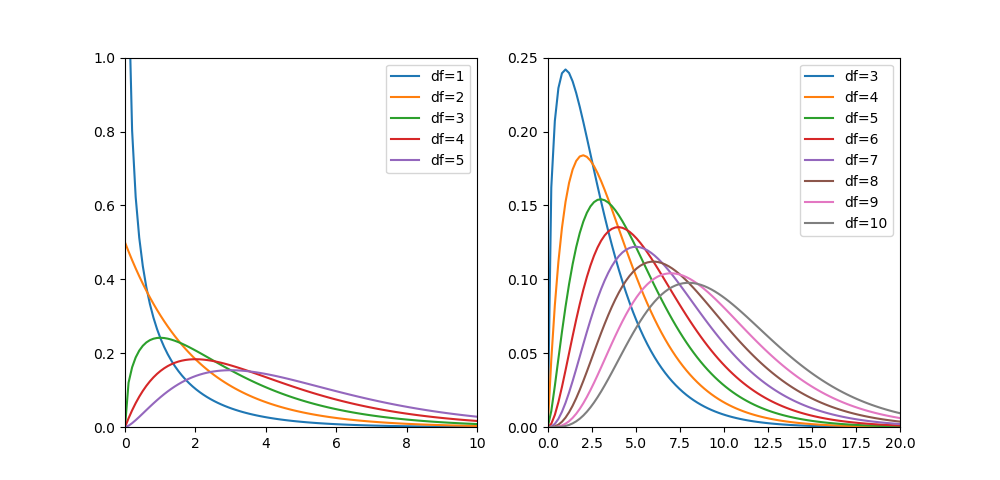
自由度と確率分布の関係

自由度kを変化させたときのカイ二乗分布の確率密度は以下の通り。

χ²分布表

カイ二乗分布は左右非対称なため、左側と右側それぞれの確率値に対するzの値を得る必要がある。以下の計算は、scipy.stats.chi2.ppf()の計算に準拠して、最上段の確率以下となるzの値を示している。

	0.005	0.01	0.025	0.05	0.1	0.9	0.95	0.975	0.99	0.995
5	0.412	0.554	0.831	1.145	1.610	9.236	11.070	12.833	15.086	16.750
6	0.676	0.872	1.237	1.635	2.204	10.645	12.592	14.449	16.812	18.548
7	0.989	1.239	1.690	2.167	2.833	12.017	14.067	16.013	18.475	20.278
8	1.344	1.646	2.180	2.733	3.490	13.362	15.507	17.535	20.090	21.955
9	1.735	2.088	2.700	3.325	4.168	14.684	16.919	19.023	21.666	23.589
10	2.156	2.558	3.247	3.940	4.865	15.987	18.307	20.483	23.209	25.188
11	2.603	3.053	3.816	4.575	5.578	17.275	19.675	21.920	24.725	26.757
12	3.074	3.571	4.404	5.226	6.304	18.549	21.026	23.337	26.217	28.300
13	3.565	4.107	5.009	5.892	7.042	19.812	22.362	24.736	27.688	29.819
14	4.075	4.660	5.629	6.571	7.790	21.064	23.685	26.119	29.141	31.319
15	4.601	5.229	6.262	7.261	8.547	22.307	24.996	27.488	30.578	32.801
16	5.142	5.812	6.908	7.962	9.312	23.542	26.296	28.845	32.000	34.267
17	5.697	6.408	7.564	8.672	10.085	24.769	27.587	30.191	33.409	35.718
18	6.265	7.015	8.231	9.390	10.865	25.989	28.869	31.526	34.805	37.156
19	6.844	7.633	8.907	10.117	11.651	27.204	30.144	32.852	36.191	38.582
20	7.434	8.260	9.591	10.851	12.443	28.412	31.410	34.170	37.566	39.997
30	13.787	14.953	16.791	18.493	20.599	40.256	43.773	46.979	50.892	53.672
40	20.707	22.164	24.433	26.509	29.051	51.805	55.758	59.342	63.691	66.766
50	27.991	29.707	32.357	34.764	37.689	63.167	67.505	71.420	76.154	79.490
60	35.534	37.485	40.482	43.188	46.459	74.397	79.082	83.298	88.379	91.952
70	43.275	45.442	48.758	51.739	55.329	85.527	90.531	95.023	100.425	104.215
80	51.172	53.540	57.153	60.391	64.278	96.578	101.879	106.629	112.329	116.321
90	59.196	61.754	65.647	69.126	73.291	107.565	113.145	118.136	124.116	128.299
100	67.328	70.065	74.222	77.929	82.358	118.498	124.342	129.561	135.807	140.169

なお、これらの値はPythonのscipy.stats.chi2を用いて計算した。

import numpy as np
import scipy.stats as stats

probs = np.array([0.005, 0.01, 0.025, 0.05, 0.1, 0.9, 0.95, 0.975, 0.99, 0.995])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}" \
                   "{1[5]:>7}{1[6]:>7}{1[7]:>7}{1[8]:>7}{1[9]:>7}"
fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}" \
                 "{1[5]:7.3f}{1[6]:7.3f}{1[7]:7.3f}{1[8]:7.3f}{1[9]:7.3f}"

print(fmt_header.format(" ", probs))
for df in range(5, 21):
    print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))
for df in range(30, 101, 10):
    print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))

import numpy as np

import scipy.stats as stats

probs = np.array([0.005, 0.01, 0.025, 0.05, 0.1, 0.9, 0.95, 0.975, 0.99, 0.995])

fmt_header = "{0:>2}{1[0]:>7}{1[1]:>7}{1[2]:>7}{1[3]:>7}{1[4]:>7}" \

"{1[5]:>7}{1[6]:>7}{1[7]:>7}{1[8]:>7}{1[9]:>7}"

fmt_data = "{0:2d}{1[0]:7.3f}{1[1]:7.3f}{1[2]:7.3f}{1[3]:7.3f}{1[4]:7.3f}" \

"{1[5]:7.3f}{1[6]:7.3f}{1[7]:7.3f}{1[8]:7.3f}{1[9]:7.3f}"

print(fmt_header.format(" ", probs))

for df in range(5, 21):

print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))

for df in range(30, 101, 10):

print(fmt_data.format(df, stats.chi2.ppf(probs, df=df)))

4件のコメント

コメント失礼します。
カイの二乗分布表をscipy.stats.chi2を使い計算されたと思うのですが、この結果をそのままエクセルに出力することは可能でしょうか？今試行錯誤しているのですがなかなかうまくいかず解決策が思いつきません。もしよろしければご教授頂きたいです。よろしくお願いします

返信

tau より:

2022-10-18 06:05

コメントいただいてありがとうございました。
返信が遅くなってすみません。
付け焼刃ですが、以下の方法で読み込んでみました。
(1) fmt_dataを以下のように変更
　fmt_data = “{1[0]:7.3f},{1[1]:7.3f},{1[2]:7.3f},{1[3]:7.3f},{1[4]:7.3f},” \
　 “{1[5]:7.3f},{1[6]:7.3f},{1[7]:7.3f},{1[8]:7.3f},{1[9]:7.3f}”
　※先頭の数を削除してデータ間にカンマを入れる
　※先頭の数を残すかどうかは好みで
(2) fmt_headerの出力をさせない
　#print(fmt_header.format(” “, probs))
　※これも好みで
(3) コンソールの出力をテキストエディタにコピーして、test.csvなどのファイル名で保存
(4) Excelから上記のファイルをCSVで読み込み（区切り文字はカンマを指定）
繰り返して作業するならファイル出力するのがいいでしょうか。
わざわざカンマを入れなくてもスペース区切りでCSV読み込みの方がいいですね。
ただし最初のコードが手抜きで最後の数行にスペースが入っていないので、7.3f→10.3fなどとする必要があります。

返信
1. 大学生 より:
  
  2022-10-29 02:26
  
  返信いただきありがとうございます。
  いろいろ試行錯誤して
  df = pd.DataFrame(data = [ stats.chi2.ppf(probs, df=i) for i in range(1, 101)], index = range(1,101),
  このような形でdataframeに入れることで解決しました。
  
  返信
  1. tau より:
    
    2022-10-30 20:00
    
    お知らせのコメントをいただいてありがとうございました。
    ライブラリーをインストールしてtoExcelを使われたのでしょうか。
    すっきりした方法ですね。
    
    返信

TauStation

カイ二乗分布～χ2分布

概要

自由度と確率分布の関係

χ²分布表

4件のコメント

コメントを残すコメントをキャンセル

概要

自由度と確率分布の関係

χ2分布表

4件のコメント

コメントを残す コメントをキャンセル

χ²分布表

コメントを残すコメントをキャンセル