母分散・標準偏差の信頼区間～カイ二乗分布

1 概要
2 手順
3 例題
4 サンプルサイズに対する信頼区間の傾向

概要

母集団が母分散σ²の正規分布に従うとき、そこから抽出されたサンプルのサンプルサイズをn、不偏分散をs²とすると、以下のχ²は自由度n−1のカイ二乗分布に従う。

(1) $\begin{equation*} \chi^2 = \frac{(n - 1) s^2}{\sigma^2} \end{equation*}$

このことを利用して、母分散の信頼区間を推定する。

手順

母集団から取り出したn個のサンプルから不偏分散s²を計算する。

(2) $\begin{equation*} s^2 = \frac{1}{n - 1} \sum_{i=1}^n (x_i - \overline{x} )^2 \end{equation*}$

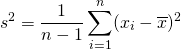
意図する確率αを定め、自由度n−1に対するχ²値を求める。両側の境界を持つ信頼区間の場合、χ²分布は左右非対称なので、左側・右側についてχ²((1−α)/2; n−1)とを算出する。

(3) $\begin{align*} {\chi^2}_- &= \chi^2\left(\frac{1 - \alpha}{2}; n - 1 \right) \\ {\chi^2}_+ &= \chi^2\left(\frac{1 + \alpha}{2}; n - 1 \right) \end{align*}$

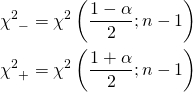
これらを用いて信頼区間を設定する。

(4) $\begin{equation*} {\chi^2}_- \le \frac{(n - 1) s^2}{\sigma^2} \le {\chi^2}_+ \end{equation*}$

これをについて以下のように変形して母分散の信頼区間を得る。

(5) $\begin{equation*} \frac{(n - 1) s^2}{{\chi^2}_+} \le \sigma^2 \le \frac{(n - 1) s^2}{{\chi^2}_-} \end{equation*}$

例題

e-statの身長・体重に関する国民健康・栄養調査2017年のデータから、40歳代の日本国民の身長の平均171.2cm及び標準偏差6.0cmを母集団のパラメーターとして用いる（データ数は374人）。

このパラメーターから、正規分布に従う10個の乱数を発生させた結果が以下の通り。

180.9 167.5 168.  164.8 176.4 157.4 181.7 166.6 173.1 169.7

1	180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7

これらのデータの不偏分散は56.73であり、これとサンプルサイズ10から以下のχ²統計量を準備する。

(6) $\begin{equation*} \chi^2 = \frac{(n - 1) s^2}{\sigma^2} = \frac{9 \times 56.73}{\sigma^2} = \frac{510.57}{\sigma^2} \end{equation*}$

一方、95%確率に対するカイ二乗分布の両側の値は以下のように得られる。

(7) $\begin{align*} {\chi^2}_- &= \chi^2(0.025; 9) = 2.7\\ {\chi^2}_+ &= \chi^2(0.975; 9) = 19.02 \end{align*}$

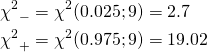
これらからχ²統計量の信頼区間を設定。

(8) $\begin{equation*} 2.7 \le \frac{510.57}{\sigma^2} \le 19.02 \end{equation*}$

移項してσ²及びσの信頼区間を得る。

(9) $\begin{gather*} \frac{510.57}{19.02} \le \sigma^2 \le \frac{510.57}{2.7} \\ 26.84 \le \sigma^2 \le 189.1 \\ 5.18 \le \sigma \le 13.75 \end{gather*}$

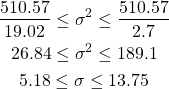
ところで、不偏分散s² = 56.73やその平方根s = 7.53は、信頼区間の中央ではなくかなり左に寄っていることがわかる。

(10) $\begin{align*} &\frac{56.73 - 26.84}{189.1 - 26.84} \approx 0.184 \\ &\frac{7.53 - 5.2}{13.7 - 5.2} \approx 0.274 \end{align*}$

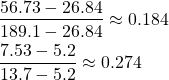
これはカイ二乗分布の確率密度が左右非対称であることに由来している。もし同じ不偏分散が100個のデータから得られたものだとするとカイ二乗分布の確率密度関数は左右対称に近づき、推定値は信頼区間の中央に近くなることが予想される。まずn = 100に対するχ²値は以下のようになる。

(11) $\begin{equation*} \chi^2 = \frac{99 \times 56.73}{\sigma^2} \approx \frac{5616}{\sigma^2} \end{equation*}$

また、95%確率に対するカイ二乗分布の両側の値は以下のように得られる。

(12) $\begin{align*} {\chi^2}_- &= \chi^2(0.025; 99) = 72.50\\ {\chi^2}_+ &= \chi^2(0.975; 99) = 127.28 \end{align*}$

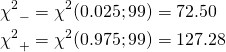
σ²およびσの信頼区間は以下のようになる。

(13) $\begin{gather*} 72.50 \le \frac{5616}{\sigma^2} \le 127.28 \\ \frac{5616}{127.28} \le \sigma^2 \le \frac{5616}{72.50} \\ 44.12 \le \sigma^2 \le 77.46 \\ 6.64 \le \sigma \le 8.80 \end{gather*}$

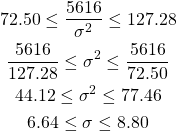
不偏分散s² = 56.73やその平方根s = 7.53の信頼区間の中での位置を見てみると、中央に近くなっていることがわかる。

(14) $\begin{align*} &\frac{56.73 - 44.12}{77.46 - 44.12} \approx 0.378 \\ &\frac{7.53 - 6.64}{8.80 - 6.64} \approx 0.412 \end{align*}$

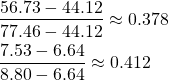
サンプルサイズに対する信頼区間の傾向

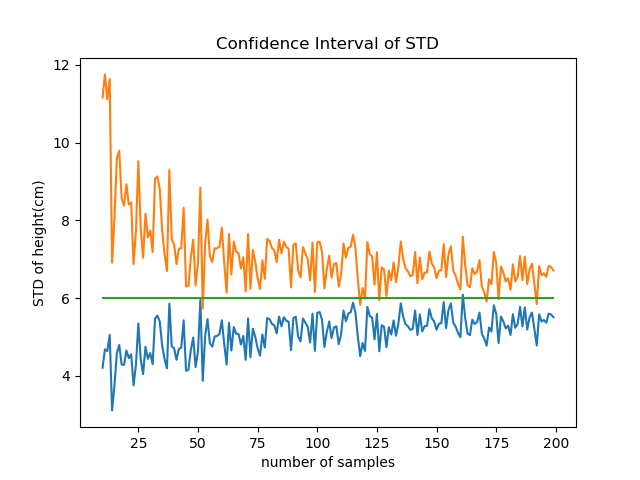
サンプルサイズを大きくしていったときの標準偏差の信頼区間の傾向は以下の通り。母集団の標準偏差に対して上側区間の方が広く、下側区間の方が狭くなっている。サンプルサイズが大きくなるとこの差は小さくなるが、それでも若干のインバランスは残っている。

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

np.random.seed(0)

h_pop_mean = 171.2
h_pop_std = 6
h_pop_var = h_pop_std**2

sample_size_list = range(10, 200)
prob_lower = 0.025
prob_upper = 0.975

fig, ax = plt.subplots()

std_cil_list = []
std_cir_list = []
for n in sample_size_list:
    h_smp = stats.norm.rvs(loc=h_pop_mean, scale=h_pop_std, size=n)
    uvar = np.var(h_smp, ddof=1)
    chil = stats.chi2.ppf(prob_lower, df=n-1)
    chir = stats.chi2.ppf(prob_upper, df=n-1)
    std_cil_list.append(np.sqrt((n - 1) * uvar / chir))
    std_cir_list.append(np.sqrt((n - 1) * uvar / chil))

ax.plot(sample_size_list, std_cil_list)
ax.plot(sample_size_list, std_cir_list)
ax.plot(sample_size_list, [h_pop_std]*len(sample_size_list))

ax.set_xlabel("number of samples")
ax.set_ylabel("STD of height(cm)")
ax.set_title("Confidence Interval of STD")

plt.show()

import numpy as np

import scipy.stats as stats

import matplotlib.pyplot as plt

np.random.seed(0)

h_pop_mean = 171.2

h_pop_std = 6

h_pop_var = h_pop_std**2

sample_size_list = range(10, 200)

prob_lower = 0.025

prob_upper = 0.975

fig, ax = plt.subplots()

std_cil_list = []

std_cir_list = []

for n in sample_size_list:

h_smp = stats.norm.rvs(loc=h_pop_mean, scale=h_pop_std, size=n)

uvar = np.var(h_smp, ddof=1)

chil = stats.chi2.ppf(prob_lower, df=n-1)

chir = stats.chi2.ppf(prob_upper, df=n-1)

std_cil_list.append(np.sqrt((n - 1) * uvar / chir))

std_cir_list.append(np.sqrt((n - 1) * uvar / chil))

ax.plot(sample_size_list, std_cil_list)

ax.plot(sample_size_list, std_cir_list)

ax.plot(sample_size_list, [h_pop_std]*len(sample_size_list))

ax.set_xlabel("number of samples")

ax.set_ylabel("STD of height(cm)")

ax.set_title("Confidence Interval of STD")

plt.show()

TauStation

母分散・標準偏差の信頼区間～カイ二乗分布

概要

手順

例題

サンプルサイズに対する信頼区間の傾向

コメントを残すコメントをキャンセル

概要

手順

例題

サンプルサイズに対する信頼区間の傾向

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル