概要
母集団の分散がわかっている場合の、母平均の信頼区間の推定について。
信頼区間の推定の考え方は以下の通り。
- サンプルを抽出し、標本平均
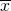 を求める
を求める - 既知の分散σ2から標本平均は正規分布N(μ, σ2/n)に従う
- 標本平均をμ, σ2/nで標準化し、標準正規分布の信頼確率αに対する信頼区間を設定
- 母平均μの信頼区間を計算
手順
まず、母集団からn個のサンプルx1, …, xnを抽出し、その平均を求める。
(1) 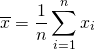
次に平均と分散で標準化した変数に対して、意図する確率値αに対する標準正規分布の確率変数値zを使って信頼区間を設定。両側の境界を持つ信頼区間の場合は以下のようになる。
(2) ![]()
これを移項してμの信頼区間として表示。
(3) ![]()
信頼確率αに対応する標準正規分布のzを設定してμの信頼区間を算出する。たとえば両側95%信頼区間なら、片側2.5%確率に対応する1.96など、標準正規分布のzの値はこちらを参照。
(4) ![]()
例題
e-statの身長・体重に関する国民健康・栄養調査2017年のデータから、40歳代の日本国民の身長の平均171.2cm及び標準偏差6.0cmを母集団のパラメーターとして用いる(データ数は374人)。
このパラメーターから、正規分布に従う10個の乱数を発生させた結果が以下の通り。
|
1 |
180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7 |
これらのデータの平均は170.6となり、これとσ2 = 36、サンプル数10、両側95%に対する1.96を用いて、信頼区間は以下のように計算される。
(5) 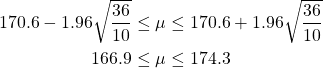
【注】上記のデータはPythonでseed(1)として発生させた。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import numpy as np np.random.seed(1) pop_mean = 171.2 pop_std = 6 n_sample = 10 x_sample = np.random.normal(pop_mean, pop_std, n_sample) np.set_printoptions(precision=1) print(x_sample) print("mean = {:5.1f}".format(np.mean(x_sample))) # [180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7] # mean = 170.6 |
当初seed(0)で発生させた際には以下のようになり、95%信頼区間が母集団の平均を含まなくなった。
|
1 2 |
[181.8 173.6 177.1 184.6 182.4 165.3 176.9 170.3 170.6 173.7] mean = 175.6 |
(6) 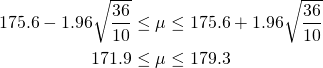
seed(0)はよく使う系列だが、このようなこともあるので乱数系列を複数変えて試すのが望ましい。
サンプルサイズに対する信頼区間の傾向
サンプルサイズを大きくしていったときの平均身長の95%信頼区間は以下の通りで、かなりばらつきながら徐々に区間幅は小さくなるが、ある程度サンプルサイズを大きくしてもあまり顕著な区間幅の減少はみられない。
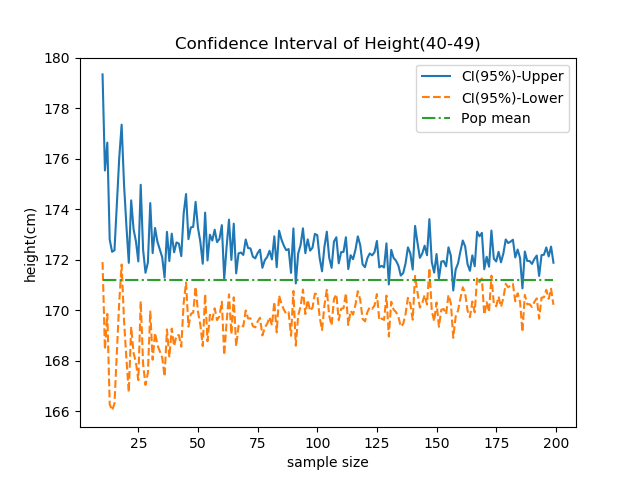
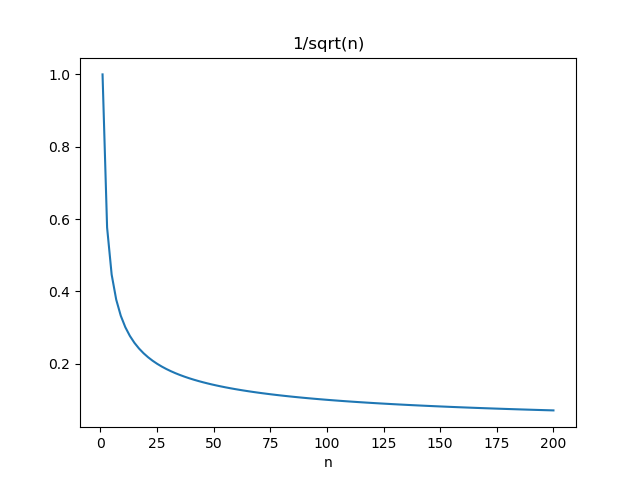
これは信頼区間に現れる![]() のグラフを描いてみると分かるが、n=20程度まで急激に小さくなり、その後の減少スピードはかなり遅いことがわかる。したがって、信頼区間を狭めようとしても、効果があるのはせいぜいデータ数50程度までということになる。
のグラフを描いてみると分かるが、n=20程度まで急激に小さくなり、その後の減少スピードはかなり遅いことがわかる。したがって、信頼区間を狭めようとしても、効果があるのはせいぜいデータ数50程度までということになる。
【補足】
本記事にいただいたコメントの通り、これの考え方は適切ではない。正しくは、![]() などのグラフを描くべき。ご指摘に感謝します。
などのグラフを描くべき。ご指摘に感謝します。
なお、1つ目のグラフの計算手順は以下の通り。
- 母集団の平均・標準偏差から、サンプルサイズを変えながら正規乱数を発生させる
- サンプルごとにサンプル平均を計算する
- サンプル平均と母分散から母平均推定の信頼区間の上限値と下限値を計算してリストに追加する
- 結果をグラフに表示する
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import numpy as np import numpy.random as rnd import matplotlib.pyplot as plt rnd.seed(0) # height of Japanese in 2017(40-49, #374) hpop_mean = 171.2 hpop_std = 6.0 hpop_var = hpop_std ** 2 sample_size_list = range(10, 200) z95 = 1.96 fig, ax = plt.subplots() hsmp_mean_conf_lower95 = [] hsmp_mean_conf_upper95 = [] for nsmp in sample_size_list: hsmp = rnd.normal(loc=hpop_mean, scale=hpop_std, size=nsmp) hsmp_mean = np.mean(hsmp) hsmp_mean_conf_lower95.append(hsmp_mean - z95 * np.sqrt(hpop_var / nsmp)) hsmp_mean_conf_upper95.append(hsmp_mean + z95 * np.sqrt(hpop_var / nsmp)) ax.plot(sample_size_list, hsmp_mean_conf_upper95, linestyle='solid', label="CI(95%)-Upper") ax.plot(sample_size_list, hsmp_mean_conf_lower95, linestyle='dashed', label="CI(95%)-Lower") ax.plot(sample_size_list, [hpop_mean]*len(sample_size_list), linestyle='dashdot', label="Pop mean") ax.set_xlabel("sample size") ax.set_ylabel("height(cm)") ax.set_title("Confidence Interval of Height(40-49)") ax.legend() plt.show() |
データの解析上とても有益な記事を拝見しています。
当方の浅学のためですが、記事中にある「信頼区間に現れる1/sqrt(n)のグラフ」の意味がよく理解できません。この値はnのみで決まっていますので、母集団の分散が異なっている場合でも共通ということですか。また、「信頼区間を挟めようと」という意味についてもご教示いただければ幸いです。
コメントありがとうございます。
ご指摘の通りです。
上の考え方は正しくなくて、本来ならσ^2/nの平方根で考えなければいけないですね。
信頼区間を狭めることについては、平均±平方根の項のレンジが信頼区間の幅なので、平方根の項が小さいほど信頼区間の幅が小さくなる=より確度の高い推定になる、と考えました。
ですので、平方根の項の減少が緩やかになって、以後あまりデータ数を増やす効果がなさそうな50程度を(これはご指摘の通り正しくないですが)を目安と考えました。
俗世の統計もので「データ数が少ないのであてにならない」として幾千ものデータを集めたりしていますが、それが過剰なのでは?との問題意識から考えてみたものです。
ご丁寧にありがとうございました。
データ数は多ければいいというものではなく、試験コストにも跳ね返ってきます。まったく同感の問題意識です。
(5)のμの値が166.9ぐらいになるように思います。
勘違いであったら申し訳ありませ。
おっしゃる通りです。
168.7としていましたが、正しくは166.88…なので166.9とするのが正しいですね。
この式はPCの電卓で計算した記憶があり、その際のミスです。
また、右側の方も値が違っていました。
172.5としていましたが、正しくは174.31…なので174.3が正でした。
ご指摘いただいてありがとうございました。