母平均の信頼区間～母分散が未知の場合

/ tau / コメントする

概要

母集団の分散がわからない場合の、母平均の信頼区間の推定について。

サンプルの平均値、不偏分散、母平均から計算されるt値がt分布に従うことを利用している。信頼区間の推定の考え方は以下の通り。

  1. サンプルを抽出し、標本平均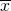\overline{x}と不偏分散s2を求める
  2. サンプルの各データを標本平均と不偏分散で標準化したt値は、サンプル数をnとすると、自由度n−1のt分布に従う
  3. t分布の自由度n−1、信頼確率αに対する値を用いて信頼区間を設定
  4. 母平均の信頼区間を計算

手順

まず、母集団からn個のサンプルx1, …, xnを抽出し、その平均と不偏分散を求める。

(1)   \begin{align*} \overline{x}_n &= \frac{1}{n}\sum_{i=1}^n x_i \\ {s^2}_n &= \frac{1}{n - 1}\sum_{i=1}^n \left( x_i - \overline{x} \right) \end{align*}

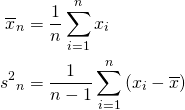
次に、これらの値から以下のt値を構成する。

(2)   \begin{equation*} t = \frac{\overline{X}_n - \mu}{\sqrt{{s^2}_n / n}} \end{equation*}

このt値が自由度n−1のt分布に従うことから、意図する確率値αに対する信頼区間を設定。両側に境界を持つ信頼区間の場合は以下のようになる。

(3)   \begin{equation*} t\left( p \le \frac{1 - \alpha}{2}; n-1 \right) \le \frac{\overline{X}_n - \mu}{\sqrt{{s^2}_n / n}} \le t\left( p \le \frac{1 + \alpha}{2}; n-1 \right) \end{equation*}

これを移項して、平均μに対する信頼区間として表示。

(4)   \begin{equation*} \overline{X}_n - t_{n-1}^{\frac{1-\alpha}{2}} \sqrt{\frac{{s^2}_n}{n}} \le \mu \le \overline{X}_n + t_{n-1}^{\frac{1+\alpha}{2}} \sqrt{\frac{{s^2}_n}{n}} \end{equation*}

tに関する値は、自由度と意図する確率の値から計算され、こちらに例示した。

例題

e-statの身長・体重に関する国民健康・栄養調査2017年のデータから、40歳代の日本国民の身長の平均171.2cm及び標準偏差6.0cmを母集団のパラメーターとして用いる（データ数は374人）。

このパラメーターから、正規分布に従う10個の乱数を発生させた結果が以下の通り。

これらのデータの平均は170.6、不偏分散は56.73。自由度10 − 1 = 9に対する両側確率95%（片側2.5%）のt値はこちらの表から2.262となることから、μの信頼区間は以下のように計算される。

(5)   \begin{gather*} 170.6 - 2.262 \sqrt{\frac{56.73}{10}} \le \mu \le 170.6 + 2.262 \sqrt{\frac{56.73}{10}} \\ 165.2 \le \mu \le 176.0 \end{gather*}

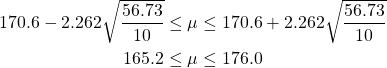
この結果は、母分散が既知の場合（168.7～172.5）に比べて区間幅が広くなっている。母分散が未知で情報が少ないのでこれは自然な結果で、式でいえば同じ確率に対するt値が標準正規分布のz値より大きいことと、不偏分散が標準偏差より大きくなることからも確認できる。

 

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です