2次元の場合
直線![]() 、点
、点![]() の距離を考える。直線と各点の記号、座標を以下のように定義する。
の距離を考える。直線と各点の記号、座標を以下のように定義する。
(1) ![]()
Step-1:直線に直交するベクトル
まず、ベクトル![]() が直線
が直線![]() に直交することを示す。直線は以下のように媒介変数表示できて、ベクトル
に直交することを示す。直線は以下のように媒介変数表示できて、ベクトル![]() は直線に平行なベクトル。
は直線に平行なベクトル。
(2) ![]()
これを直線の式に代入して、
(3) ![]()
ここで任意の![]() に対して上式が成り立つことから、
に対して上式が成り立つことから、![]() となり、ベクトル
となり、ベクトル![]() は直線に垂直であることが示された。
は直線に垂直であることが示された。
別解:点と直線の距離をパラメーター(媒介変数)によって愚直に求める方法
Step-2:法線ベクトルとの平行条件による導出
与えられた点![]() から直線
から直線![]() への垂線の足を
への垂線の足を![]() とすると、
とすると、![]() なので、以下が成り立つ。
なので、以下が成り立つ。
(4) ![]()
ここで![]() は直線
は直線![]() 上にあることを考慮し、上式の左辺を以下のように変形できる。
上にあることを考慮し、上式の左辺を以下のように変形できる。
(5) 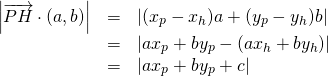
これより
(6) ![]()
3次元の場合
3次元平面の式
3次元空間内の平面は、たとえば以下のように表すことができる。
(7) ![]()
一方、3次元平面上の点と法線ベクトル![]() との直行条件から、以下のようにも表現できる。
との直行条件から、以下のようにも表現できる。
(8) 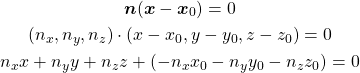
上記2つの式より、ベクトル![]() は平面に対する法線ベクトルであることがわかる。
は平面に対する法線ベクトルであることがわかる。
法線ベクトルとの平行条件
この法線ベクトルがベクトル![]() と平行であることから、
と平行であることから、
(9) ![]()
上式の左辺は以下のように変形できる。
(10) 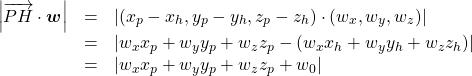
以上のことから、点![]() から三次元平面
から三次元平面![]() への距離については、以下で表される。
への距離については、以下で表される。
(11) ![]()
多次元の場合
n次元の超平面を以下の式で与える。
(12) ![]()
このとき、これまでと同様の考え方により、点![]() と上記の超平面との距離は以下で表される。
と上記の超平面との距離は以下で表される。
(13) ![]()
一番最後の計算はどのようにして行われているのでしょうか
ありがとうございます。
n次元でも理屈は同じと考えて、式(10)~(11)で単純に3成分をn成分としました。
数学的に「距離」を定義したりして導く方法もあるかと思います。