概要
k平均法(k-means clustering)はクラスタリングの手法の1つで、与えられたデータ群の特徴と初期値に基づいて、データを並列(非階層)のクラスターに分類する。
ここではk平均法の簡単な例を実装したKMeansClusteringクラスによって、その挙動を確認する。
テストケース
基本形
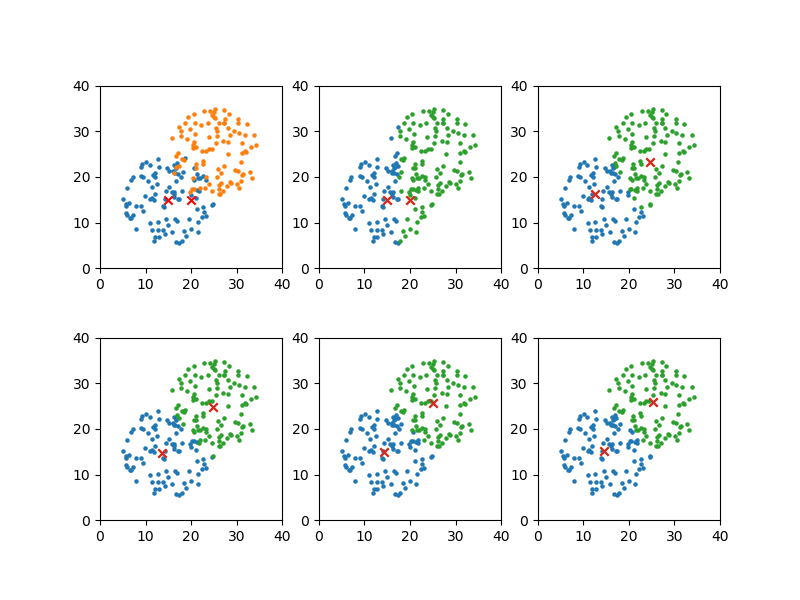
2つのクラスターがある程度明確なケースで試してみる。一定の円内にランダムに点を発生させ、そのグループを2つ近づけた例。
|
1 2 3 4 |
x_means[0], y_means[0] = 15, 15 x_means[1], y_means[1] = 20, 15 plot_steps = [0, 1, 2, 4, 6] |
以下のように、重なった部分は仕方がないが、かなり元のグループに近い分類となっている。
|
1 2 3 |
convergion times = 7 [14.567003574164632, 15.215775486294216] [25.31190419286806, 25.871321239241027] |
初期値を変えた場合
代表点の初期値を変えて実行してみる。
|
1 2 3 4 |
x_means[0], y_means[0] = 25, 25 x_means[1], y_means[1] = 25, 30 plot_steps = [0, 1, 2, 4, 8] |
上記とはかなり離れた初期値を設定しても、解は同じになる。
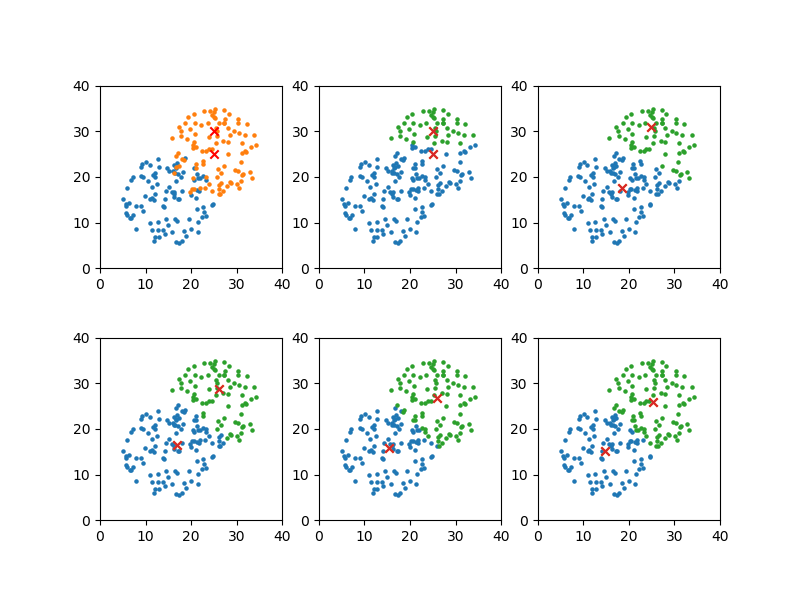
収束解も上記と全く同じ値になる。
|
1 2 3 |
convergion times = 9 [14.567003574164632, 15.215775486294216] [25.31190419286806, 25.871321239241027] |
クラスターが不明確な場合
先の結果だけを見ると、かなり初期値がずれてもクラス分類は安定なように見える。
そこで次に、元々の分布に明確なクラス分けが見えない場合に3つのクラスターに分ける例を考える。
初期値1
|
1 2 3 4 5 |
x_means[0], y_means[0] = 10, 18 x_means[1], y_means[1] = 18, 18 x_means[2], y_means[2] = 25, 18 plot_steps = [0, 1, 4, 8, 12] |
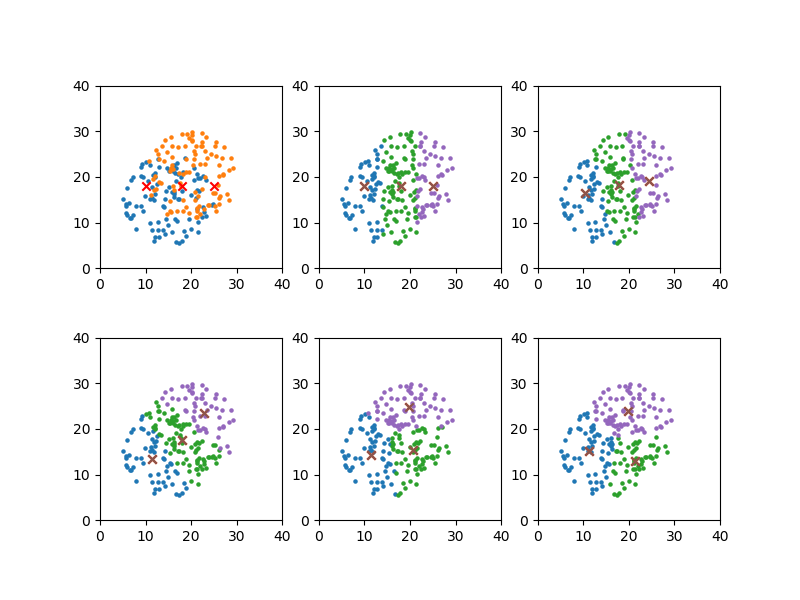
|
1 2 3 4 |
convergion times = 13 [11.359345006841108, 15.215511281942952] [21.33481062455269, 13.05930376628775] [19.777630465074534, 23.850681586725297] |
初期値2
上記に対して初期値を変更。
|
1 2 3 4 5 |
_means[0], y_means[0] = 18, 10 x_means[1], y_means[1] = 18, 18 x_means[2], y_means[2] = 18, 25 plot_steps = [0, 1, 4, 8, 10] |
データは同じだが、クラスター分けは違ってきている。
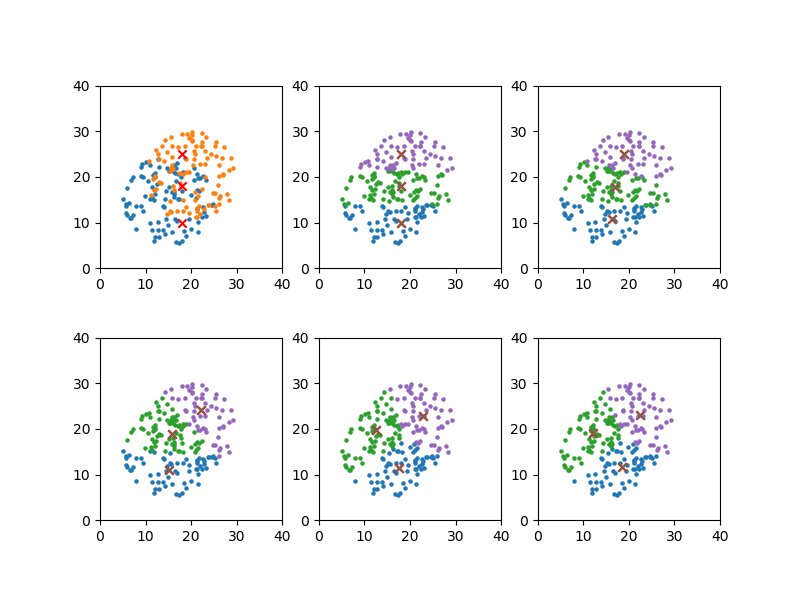
|
1 2 3 4 |
convergion times = 11 [18.43160436224161, 11.596987217637075] [12.210575780454143, 19.032933149086162] [22.418606246186307, 23.158839350112153] |
極端な例
次に、元の分布でクラスターが見いだせないような極端な場合を考える。
初期値1
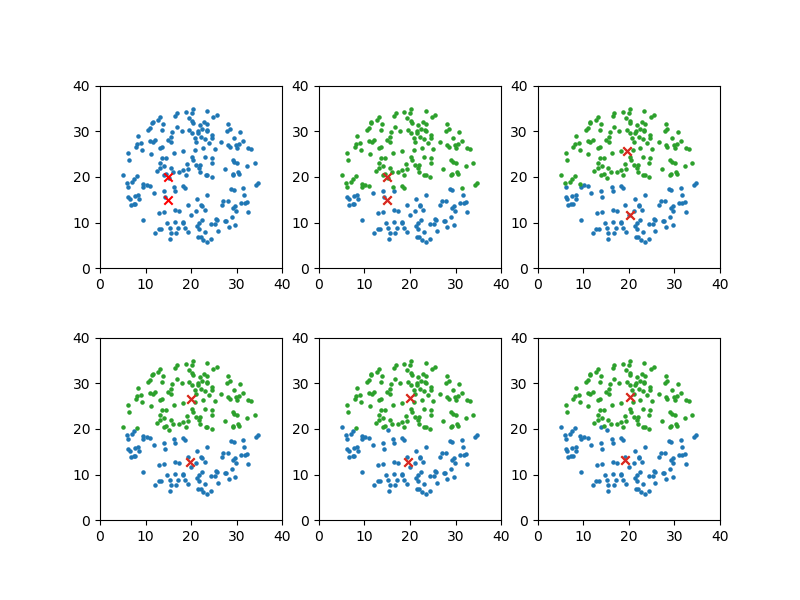
代表点の初期値は縦に並んでおり、クラスターも縦方向に分割されている。
|
1 2 3 4 |
x_means[0], y_means[0] = 15, 15 x_means[1], y_means[1] = 15, 20 plot_steps = [0, 1, 3, 5, 8] |
|
1 2 3 |
convergion times = 9 [19.1770479839392, 13.104941433078057] [20.361677232475646, 26.9785132838531] |
初期値2
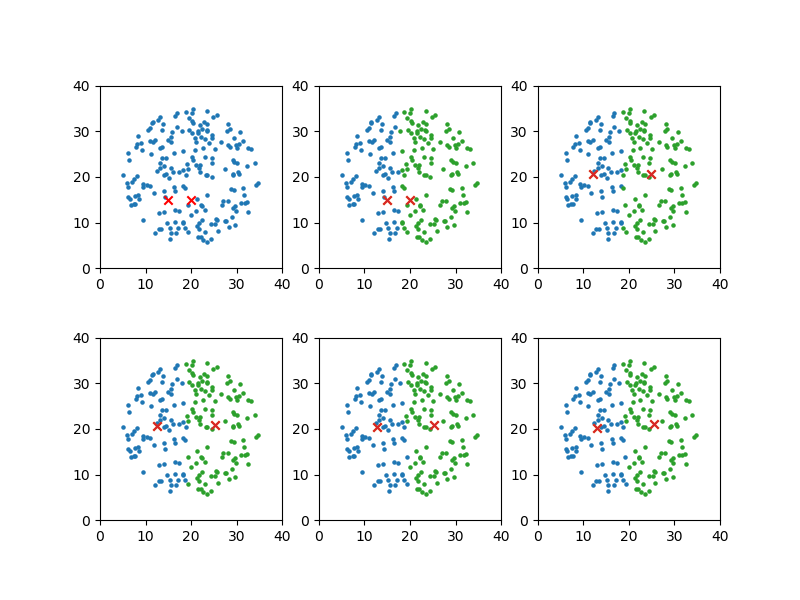
全く同じデータで代表点の初期値を横に並べた場合、クラスター分けは大きく異なっている。
|
1 2 3 4 5 6 7 |
x_means[0], y_means[0] = 15, 15 x_means[1], y_means[1] = 20, 15 x_lim = 40 y_lim = 40 plot_steps = [0, 1, 2, 4] |
|
1 2 3 |
convergion times = 5 [12.933983667295676, 20.22594500107436] [25.46963894609307, 21.15223763731067] |
3クラスター
最後に、元のデータでクラスターがかなり明確な場合を試してみる。
初期値1
|
1 2 3 4 5 |
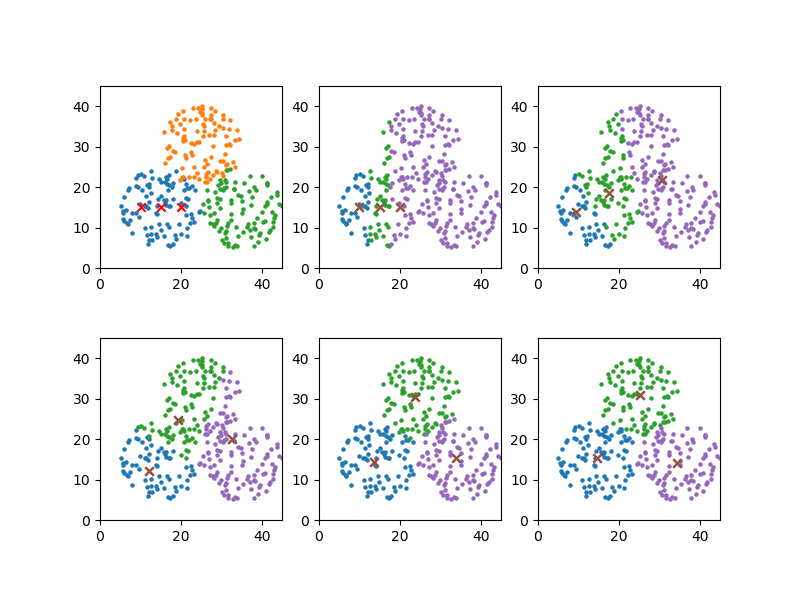
_means[0], y_means[0] = 10, 15 x_means[1], y_means[1] = 15, 15 x_means[2], y_means[2] = 20, 15 plot_steps = [0, 2, 4, 6, 9] |
初期値が隅の方から始まっていても、3つのクラスターによく分かれている。
|
1 2 3 4 |
convergion times = 10 [14.610459971900003, 15.428114490958492] [25.252313933530775, 30.84369233062165] [34.43506243558404, 14.084017148769334] |
初期値2
|
1 2 3 4 5 |
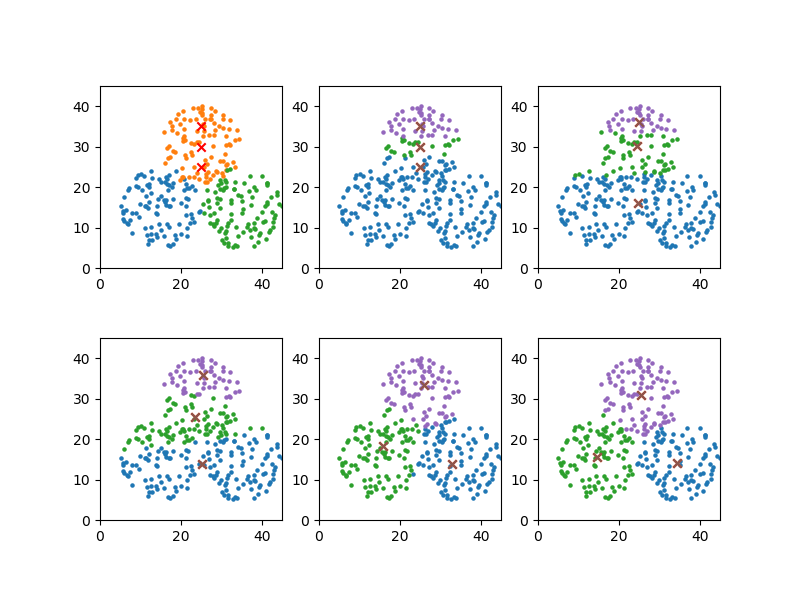
x_means[0], y_means[0] = 25, 25 x_means[1], y_means[1] = 25, 30 x_means[2], y_means[2] = 25, 35 plot_steps = [0, 1, 3, 6, 10] |
初期値の場所や並びがかなり異なっていても、クラスター分けは安定している。
|
1 2 3 4 |
convergion times = 11 [34.43506243558404, 14.084017148769334] [14.665546643275666, 15.615970568228104] [25.413807412324008, 30.963999916166244] |
まとめ
k平均法は初期値によって解が変動するとされているが、明らかにクラスターが明確な場合には解は安定している。
ただしそのようなケースは、特徴量の数が少なく分布が一目瞭然の場合に相当するので、特徴量が多く一目ではそのクラスターがわかりにくいような場合には、やはり初期値の取り方に大きく影響されるものと考えられる。