定義
Ridge回帰は単純な多重回帰の損失関数に対してL2正則化項を加え、多重共線性に対する正則化を図った。Lasso解析はこれに対してL1正則化項を加えて最小化する(正則化の意味についてはこちら)。
(1) 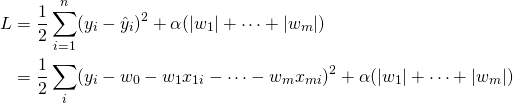
L1正則化の意味
準備
L2正則化は各重み係数が全体として小さくなるように制約がかかったが、L1正則化では値がゼロとなる重み係数が発生する。このことを確認する。
係数wを求めるためには損失関数Lを最小化すればよいが、Ridge回帰とは異なりL1正則化項は通常の解析的な微分はできない。
(2) 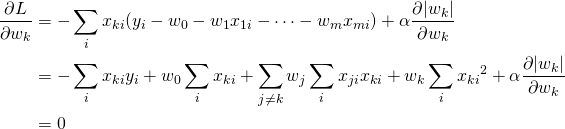
ここで![]() と表し、左辺のwk以外に関わる項をMk、wkの係数となっている2乗和をSkkと表す。
と表し、左辺のwk以外に関わる項をMk、wkの係数となっている2乗和をSkkと表す。
(3) ![]()
場合分け
ここで|wk|’についてはwkの符号によって以下の値をとる。
(4) ![]()
これらを式(3)に適用する。まずwk < 0に対しては
(5) 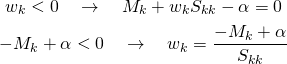
またwk > 0に対しては、
(6) 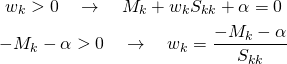
以上をまとめると、
(7) 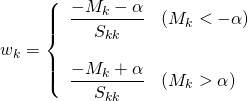
劣微分の導入
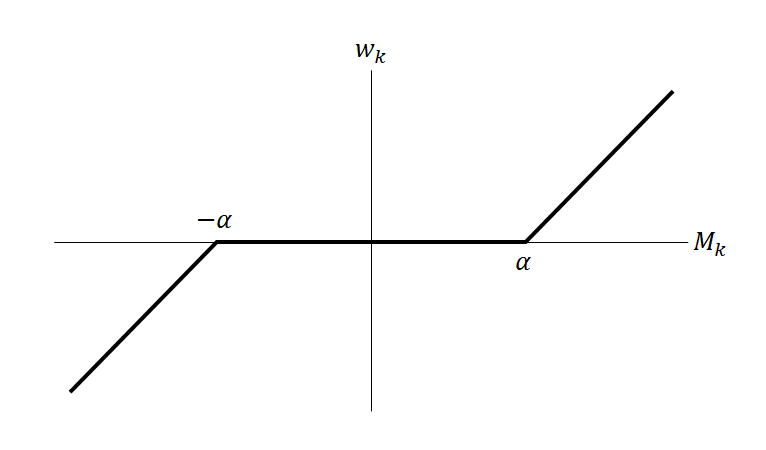
式(7)で−α ≤ Mk ≤ αについては得られていない。Mk → ±αについてそれぞれの側から極限を計算すると0となるのでその間も0でよさそうだが、その保証はない。
ここでこちらのサイトのおかげで”劣微分(subdifferential)”という考え方を知ることができた。|wk|’についてwk = 0では解析的に微分不可能だが、その両側から極限をとった微分係数の範囲の集合を微分係数とするという考え方のようだ。
(8) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{d |x|}{dx} = \left\{ \begin{array}{cl} -1 & (x < 0) \\ \left[ -1, 1 \right] & (x = 0) \\ 1 & (x > 0) \end{array} \right. \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-1aadd0e8e3a8da8daf0db2c69a068fd7_l3.png)
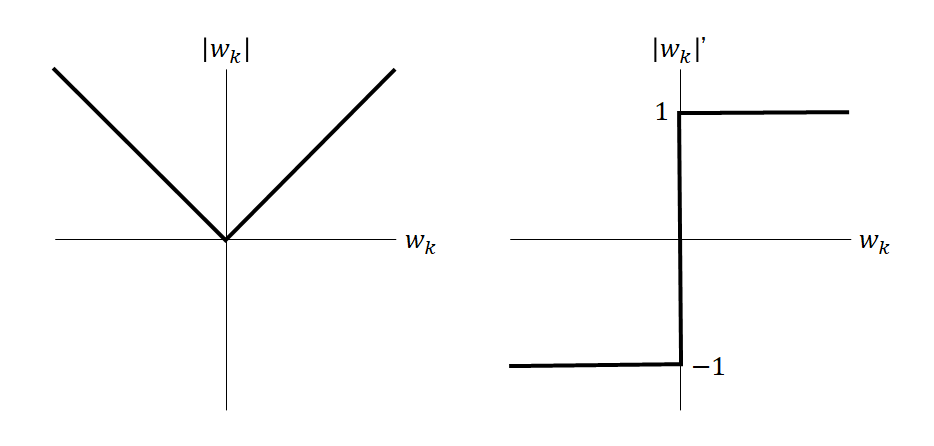
そこで、wk = 0に対してこの劣微分を適用してみる。
(9) ![]()
以上のことから、重みwkについて以下のようになり、−α≤Mk≤αの範囲ではwk = 0となることがわかる。
(10) 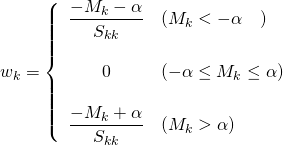
すなわちL1正則化の場合、ハイパーパラメータαは重み係数の大きさを制限すると同時に重み係数がゼロとなるような効果も持ち、αが大きいほど多くの重み係数がゼロとなりやすい。
参考サイト
本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。
Lassoを数式から実装まで(理論編)~Miidas Research