線形モデルの多層化
“Pythonではじめる機械学習”の写経。多層パーセプトロン(Multilayer perceptron : MLP)はフィードフォワード・ニューラルネットワークとも呼ばれる。
まず、線形モデルを以下の式で表す。
(1) ![]()
n = 3の場合について図示すると、以下のように表せる。左側のノードの特徴量xiに対して、wiによる重み付き和を計算している。
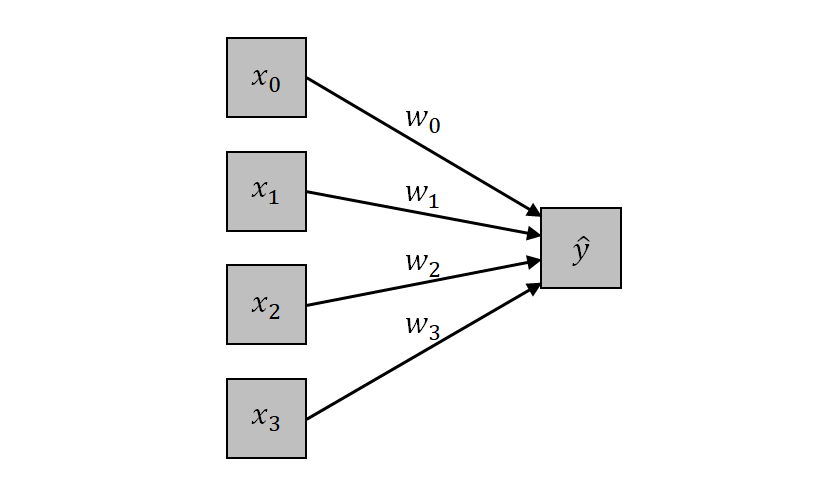
MLPは、この構造に中間層を導入し、中間層に隠れユニット(hidden units)を配置する。特徴量入力はまず隠れユニットに対して重み付き線形和を計算し、その後に隠れユニットの出力の重み付き線形和を出力とする。
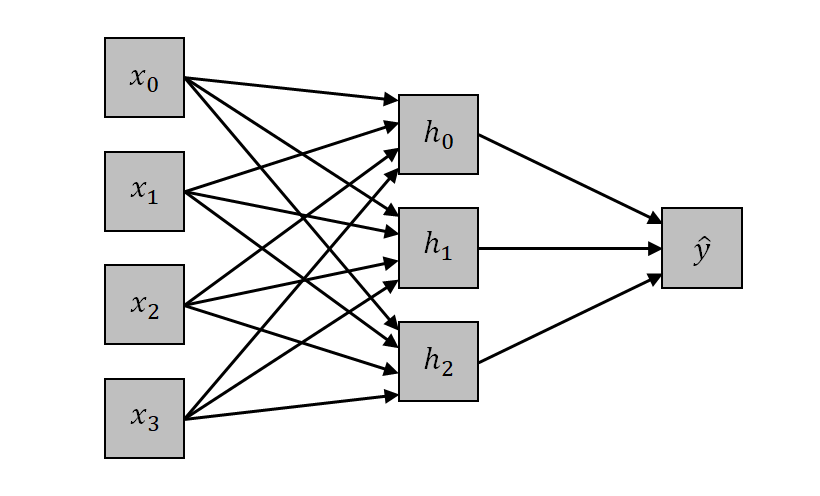
特徴量xi (i = 0~n)の隠れユニットhj (j = 0~m)に対する重みをwij、切片をbjとすると、hjへの入力となる重み付き線形和は以下のようになる。
(2) ![]()
また、隠れユニットhjの出力![]() に対する重みをvj、切片をcとすると、出力への重み付き線形和は以下のようになる。
に対する重みをvj、切片をcとすると、出力への重み付き線形和は以下のようになる。
(3) 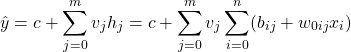
これは結局、xiに対する重み付き線形和となる。たとえば特徴量0~3、隠れユニット0~2の場合は以下のとおり。
(4) 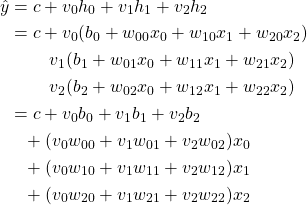
非線形活性化関数
単純な線形和をいくら多層化しても、結果は特徴量の線形和にしかならない。そこで、隠れユニットの入力に対して非線形関数を適用して出力とし、複雑・柔軟な動作を可能とする。
このような関数を活性化関数(activation function)あるいは伝達関数(transfer function)と呼び、様々な種類がある。書籍では、このうちReLU (Rectified linear unit)とtanh (hyperbolic tangent)が紹介されている。ReLUは以下の式で表され、負の値が採用しえない(計算過程での)ノイズであるような場合に好都合らしい。tanhは(−∞, +∞)の入力に対して(−1, +1)の出力を返す。
(5) 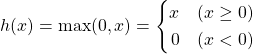
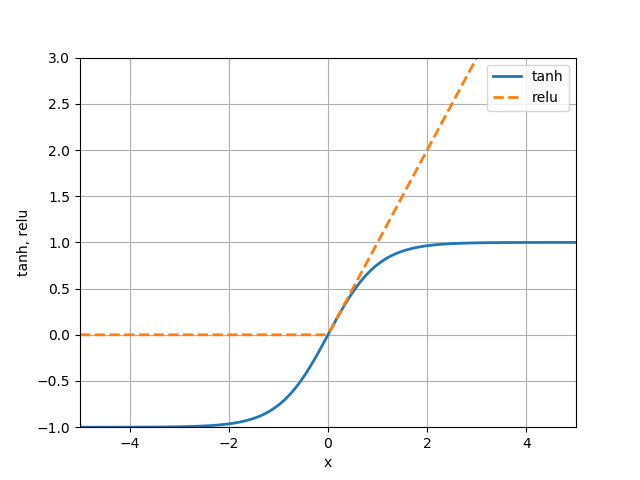
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np import matplotlib.pyplot as plt xmin, xmax = -5, 5 ymin, ymax = -1, 3 x = np.linspace(xmin, xmax, 100) tanh = np.tanh(x) relu = np.maximum(x, 0) fig, ax = plt.subplots() ax.plot(x, tanh, label="tanh", linewidth=2,) ax.plot(x, relu, label="relu", linewidth=2, linestyle='dashed') ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.set_xlabel("x") ax.set_ylabel("tanh, relu") ax.grid(True) ax.legend() plt.show() |
ニューラルネットワークのチューニング
two moonsデータでの確認
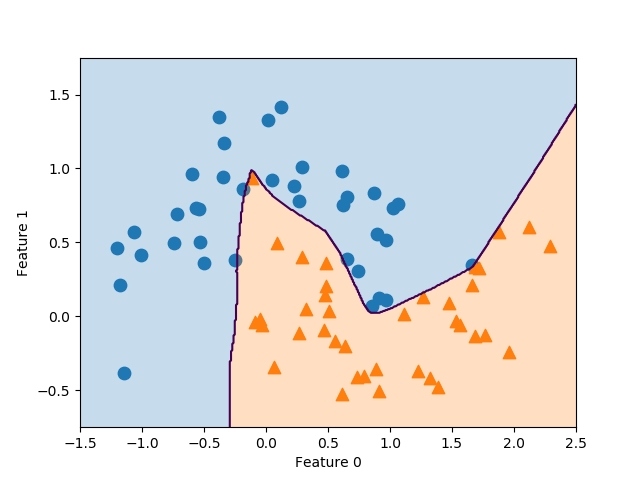
two moonsデータセットに対してMLPを適用する。隠れユニットの数はデフォルトの100としている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_moons from sklearn.model_selection import train_test_split from sklearn.neural_network import MLPClassifier xmin, xmax = -1.5, 2.5 ymin, ymax = -0.75, 1.75 X, y = make_moons(n_samples=100, noise=0.25, random_state=3) X_train, X_test, y_train, y_test = \ train_test_split(X, y, stratify=y, random_state=42) mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train) f0 = np.linspace(xmin, xmax, 400) f1 = np.linspace(ymin, ymax, 400) f0, f1 = np.meshgrid(f0, f1) pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape) fig, ax = plt.subplots() color0, color1 = 'tab:blue', 'tab:orange' Xtr0 = X_train[y_train==0] Xtr1 = X_train[y_train==1] ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=80, color=color0) ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=80, color=color1) ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25) ax.contour(f0, f1, pred, levels=[0.5]) ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.set_xlabel("Feature 0") ax.set_ylabel("Feature 1") plt.show() |
隠れユニット数と決定境界
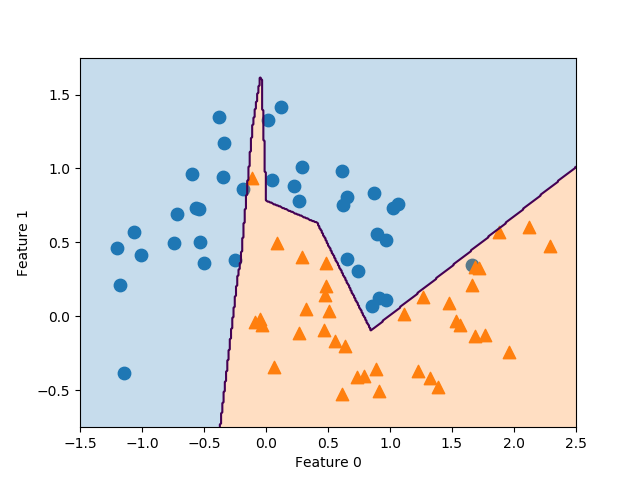
隠れユニット数を10とした場合の結果は数の通り。先のユニット数100の場合に比べて、決定境界が折れ線になっている。
隠れユニット数の指定はhidden_layer_sizes=[10]のように指定する。複数の隠れ層を表現するためにリストとなっていて、1層の場合でも1要素のリストとする。また、収束計算回数の最大値がデフォルトのmax_iter=200では収束しきれないという警告が出るため、この値を1000に引き上げている。
結果は書籍のものと少し異なっていて、上方の▲の点より上に鋭く境界が突き抜けている。いくつかパラメーターを変えてみたが、書籍のような境界の形状は再現できなかった。
|
1 2 |
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10], max_iter=1000).fit(X_train, y_train) |
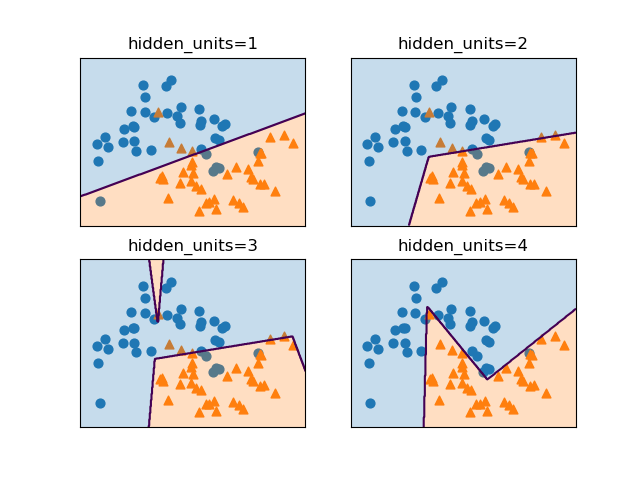
隠れユニットの数を[1]~[4]と変化させたときの決定境界の様子は以下の通りで、ユニット数が増えるにしたがって決定境界を構成する線分の数が増えている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
for i, ax in enumerate(axs.reshape(-1)): ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=40, color=color0) ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=40, color=color1) mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[i+1]).fit(X_train, y_train) pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape) ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25) ax.contour(f0, f1, pred, levels=[0.5]) ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False) ax.set_title("hidden_units={}".format(i + 1)) plt.show() |
隠れ層の数
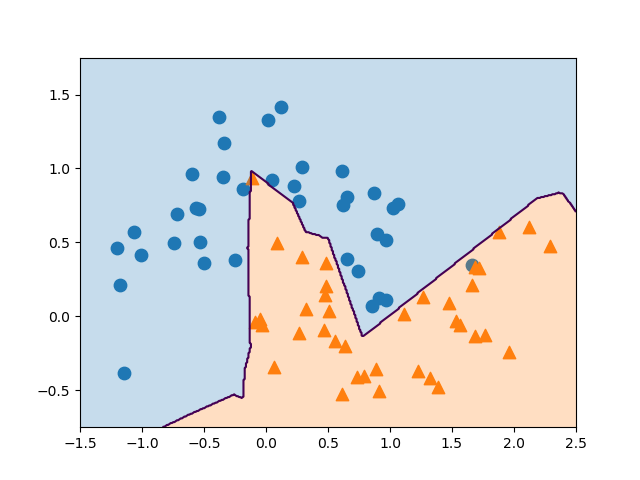
隠れユニット数が10程度でも、隠れ層の数を増やすと決定境界は滑らかになる。
|
1 2 |
mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[10, 10]).fit(X_train, y_train) |
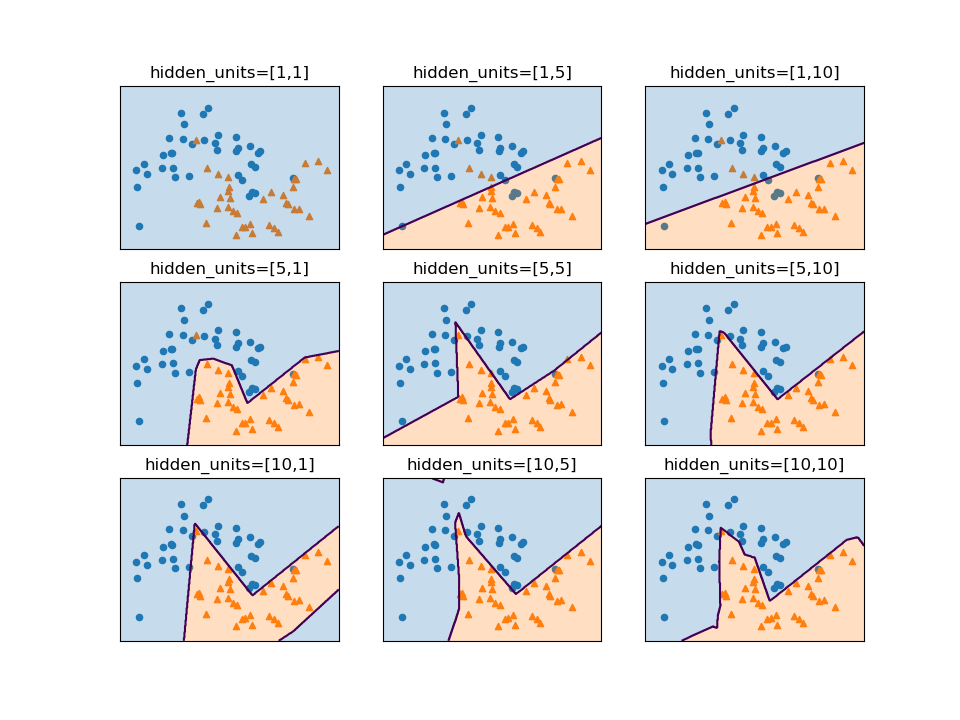
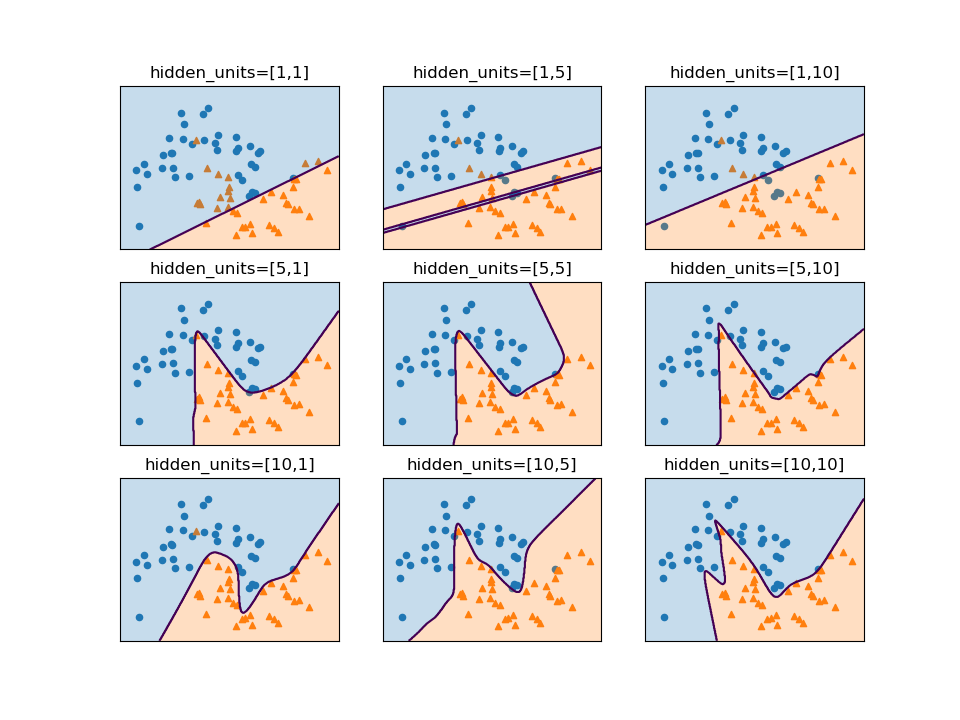
隠れ層が2層の場合に、各層のユニット数を変化させたときの決定境界の変化を見てみる。1層目のユニット数が大まかな形に影響し、2層目のユニットは決定境界の滑らかさに影響していると言えそうだ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
units0_list = [1, 5, 10] units1_list = [1, 5, 10] for row, units0 in enumerate(units0_list): for col, units1 in enumerate(units1_list): ax = axs[row, col] ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=20, color=color0) ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=20, color=color1) mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[units0, units1]).fit(X_train, y_train) pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape) ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25) ax.contour(f0, f1, pred, levels=[0.5]) ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False) ax.set_title("hidden_units=[{},{}]".format(units0, units1)) plt.show() |
活性化関数tanh
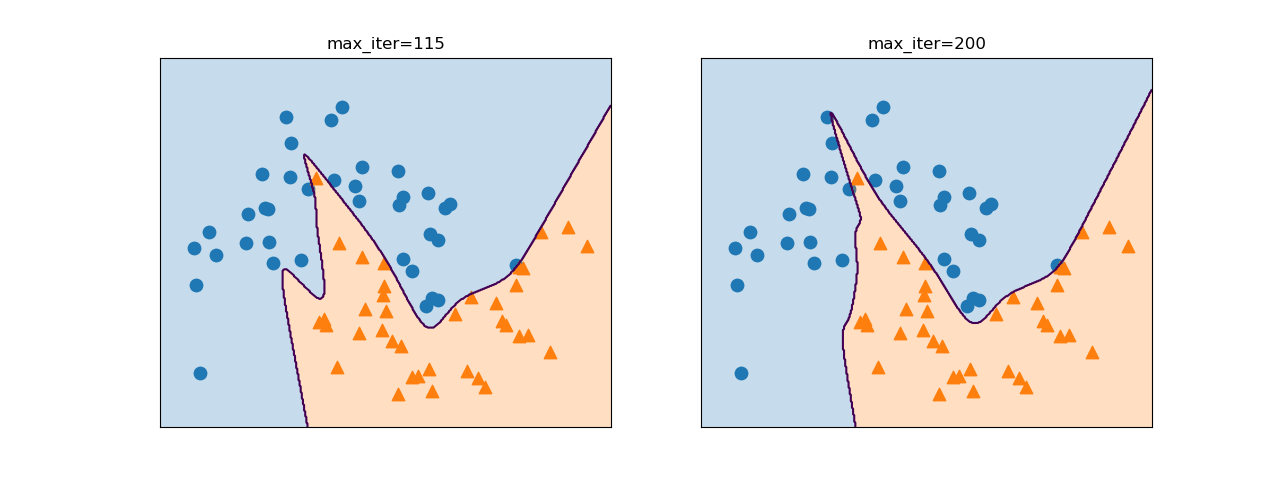
デフォルトでは非線形活性化関数にReLUが用いられるが、これをtanhとすることで下図のように決定境界が滑らかになる。デフォルトのまま(右)だと書籍のような形にならないが、最大計算回数max_iter=115と制限すると大体似たような形になる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
max_iter_list = [115, 200] for max_iter, ax in zip(max_iter_list, axs_1d): ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=80, color=color0) ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=80, color=color1) mlp = MLPClassifier(solver='lbfgs', activation='tanh', random_state=0, hidden_layer_sizes=[10, 10], max_iter=max_iter).fit(X_train, y_train) pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape) ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25) ax.contour(f0, f1, pred, levels=[0.5]) ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False) ax.set_title("max_iter={}".format(max_iter)) plt.show() |
ここでも2つの隠れ層のユニット数を変化させてみると、第1層が大まかな形、第2層が細部の表現に影響していると言えそうだ。
正則化
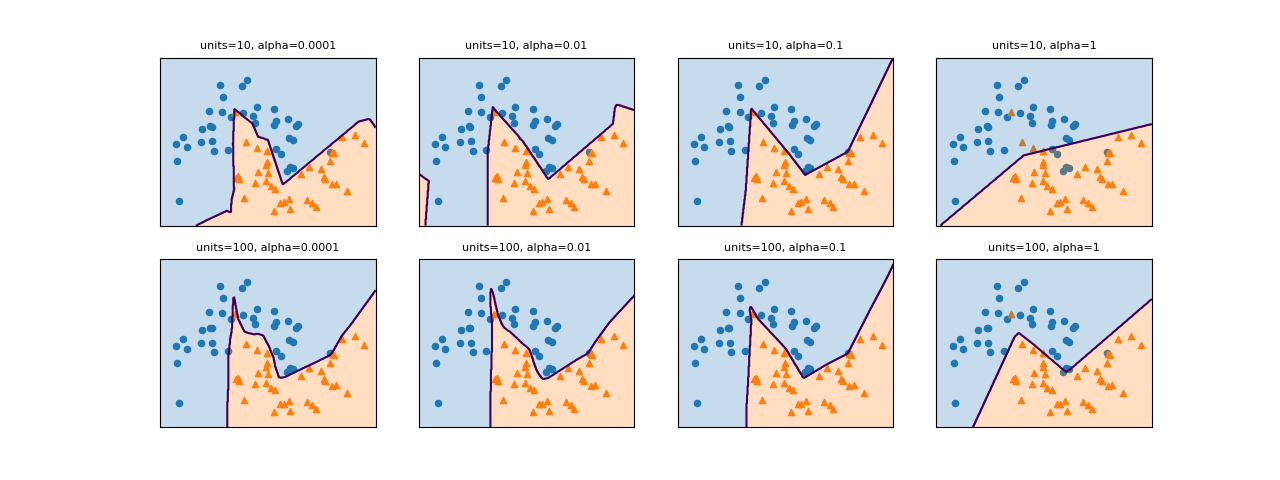
MLPClassifierはL2正則化が可能で、パラメーターalphaに大きな値を設定すると正則化を強くできる。デフォルトはalpha=0.0001で正則化が効いていない状態。
以下に、2層のユニット数[10, 10]と[100, 100]に対してalphaをデフォルトの0.0001から1.0まで変化させたときの様子を示す。ただしmax_iter=500として未収束の警告が出ないようにしている。alphaを大きくするにしたがって正則化が強くなり、決定境界がシンプルなものになっていく様子が見られる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
units = [10, 100] alphas = [0.0001, 0.01, 0.1, 1] for axr, unit in zip(axs, units): for ax, alpha in zip(axr, alphas): ax.scatter(Xtr0[:, 0], Xtr0[:, 1], marker='o', s=20, color=color0) ax.scatter(Xtr1[:, 0], Xtr1[:, 1], marker='^', s=20, color=color1) mlp = MLPClassifier(solver='lbfgs', random_state=0, hidden_layer_sizes=[unit, unit], alpha=alpha, max_iter=500).fit(X_train, y_train) pred = mlp.predict(np.vstack([f0.ravel(), f1.ravel()]).T).reshape(f0.shape) ax.contourf(f0, f1, pred, levels=1, colors=[color0, color1], alpha=0.25) ax.contour(f0, f1, pred, levels=[0.5]) ax.set_title("units={}, alpha={}".format(unit, alpha), fontsize=8) ax.set_xlim(xmin, xmax) ax.set_ylim(ymin, ymax) ax.tick_params(bottom=False, left=False, labelbottom=False, labelleft=False) plt.show() |
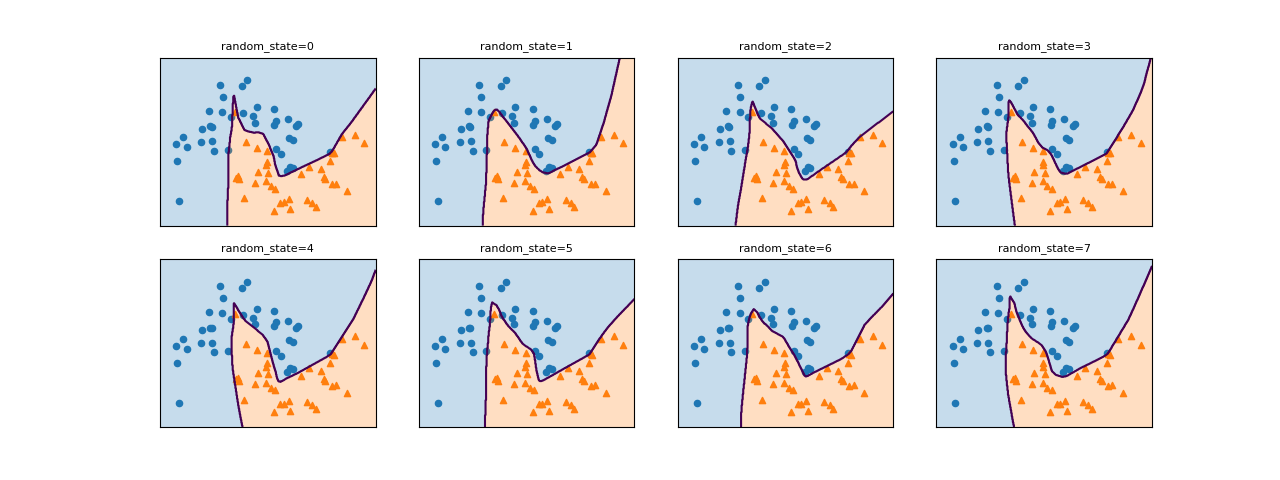
ランダムな重みづけの影響
ニューラルネットワークでは、学習開始前に各重み係数がランダムに割り当てられるため、その初期値がモデルに影響を与える。以下は同じパラメーター設定に対してrandom_stateのみを変化させたもので、決定境界の形が異なっている。
データの前処理等
MLPのBreast cancerデータセットへの適用例で、データの標準化や重み係数の分布の確認等を行っている。
今後の課題
- 総数・ユニット数と計算量の関係
- パラメーター調整のパターン
- scikit-learn以外のライブラリー(
keras,lasagna,tensor-flow) - GPUのサポート
- 収束計算のアルゴリズム(
lbfgs,adam,sgd)