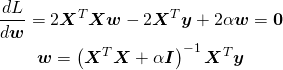Ridge回帰の理解

/ tau / コメントする

定義

Ridge回帰は多重回帰の損失関数に罰則項としてL2正則化項を加味する。正則化の意味についてはこちらに詳しくまとめている。

L2ノルムは原点からのユークリッド距離。

(1)   \begin{equation*} \| \boldsymbol{w} \| _2 = \sqrt{w_1 ^2 + \cdots + w_m^2} \end{equation*}

ただしリッジ回帰では、根号の中の二乗項で計算する。

(2)   \begin{equation*} \mathrm{minimize} \quad \sum_{i=1}^n (y_i - \hat{y}_i) + \alpha \sum_{j=1}^m w_j^2 \end{equation*}

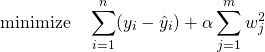
定式化

最小化すべき関数は、

(3)   \begin{align*} L &= \sum_{i=1}^n ( \hat{y}_i - y_i )^2 + \alpha ({w_1}^2 + \cdots + {w_2}^2) \\ &= \sum ( w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i )^2 + \alpha ({w_1}^2 + \cdots + {w_m}^2) \end{align*}

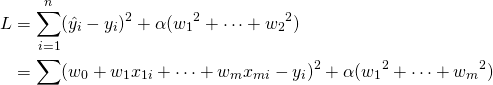
重み係数を計算するために、それぞれで偏微分してゼロとする。

(4)   \begin{align*} \frac{\partial L}{\partial w_0} &= 2 \sum (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) = 0 \\ \frac{\partial L}{\partial w_1} &= 2 \sum x_{1i} (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) + 2 \alpha w_1 = 0 \\ \vdots\\ \frac{\partial L}{\partial w_m} &= 2 \sum x_{mi} (w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} - y_i) + 2 \alpha w_m = 0\\ \end{align*}

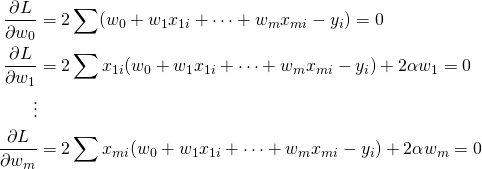
その結果得られる連立方程式は以下の通り。

(5)   \begin{align*} n w_0 + w_1 \sum x_{1i} + \cdots + w_m \sum x_{mi} &= \sum y_i \\ w_0 \sum x_{1i} + w_1 \left( \sum {x_{1i}}^2 + \alpha \right) + \cdots + w_m \sum x_{1i} x_{mi} &= \sum x_{1i} y_i \\ \vdots \\ w_0 \sum x_{mi} + w_1 \sum x_{1i} x_{mi} + \cdots+ w_m \left( \sum {x_{mi}}^2 + \alpha \right) &= \sum x_{mi} y_i \\ \end{align*}

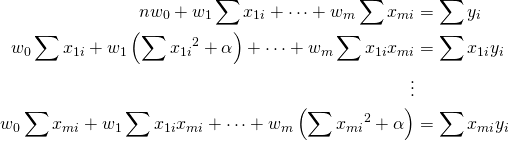
ここでそれぞれの和を記号Sと添字で表し、さらに行列表示すると以下の通り。

(6)   \begin{equation*} \left[ \begin{array}{cccc} n & S_1 & \cdots & S_m \\ S_1 & S_{11} + \alpha & & S_{1m} \\ \vdots & \vdots & & \vdots \\ S_m & S_{m1} & \cdots & S_{mm} + \alpha \end{array} \right] \left[ \begin{array}{c} w_0 \\ w_1 \\ \vdots \\ w_m \end{array} \right] = \left[ \begin{array}{c} S_y \\S_{1y} \\ \vdots \\ S_{my} \end{array} \right] \end{equation*}

ここでw_0を消去して、以下の連立方程式を得る。

(7)   \begin{align*} &\left[ \begin{array}{ccc} ( S_{11} + \alpha ) - \dfrac{{S_1}^2}{n} & \cdots & S_{1m} - \dfrac{S_1 S_m}{n} \\ \vdots & & \vdots \\ S_{m1} - \dfrac{S_m S_1}{n} & \cdots & ( S_{mm} + \alpha )- \dfrac{{S_2}^2}{n} \end{array} \right] \left[ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array} \right] \\&= \left[ \begin{array}{c} S_{1y} - \dfrac{S_1 S_y}{n} \\ \vdots \\ S_{my} - \dfrac{S_m S_y}{n} \end{array} \right] \end{align*}

これを分散・共分散で表すと、

(8)   \begin{equation*} \left[ \begin{array}{ccc} V_{11} + \dfrac{\alpha}{n} & \cdots & V_{1m} \\ \vdots & & \vdots \\ V_{m1} & \cdots & V_{mm} + \dfrac{\alpha}{n} \end{array} \right] \left[ \begin{array}{c} w_1 \\ \vdots \\ w_m \end{array} \right] = \left[ \begin{array}{c} V_{1y} \\ \vdots \\ V_{my} \end{array} \right] \end{equation*}

ここで仮に、xjiとxkiが完全な線形関係にある場合を考えてみる。x_j = a x_i + bとすると、分散・共分散の性質より、

(9)   \begin{equation*} V_{jj} = a^2V_{ii}, \; V_{ji} = V_{ij} = aV_{ii}, \; V_{jk} = V_{kj} = aV_{ji} = aV_{ij} \end{equation*}

このような場合、通常の線形回帰は多重共線性により解を持たないが、式(8)に適用すると係数行列は以下のようになる。

(10)   \begin{align*} \left[ \begin{array}{ccccccc} V_{11} + \dfrac{\alpha}{n} & \cdots & V_{1i} & \cdots & aV_{1i} & \cdots & V_{1m}\\ \vdots && \vdots && \vdots && \vdots\\ V_{i1} & \cdots & V_{ii} + \dfrac{\alpha}{n} & \cdots & aV_{ii} & \cdots & V_{im}\\ \vdots && \vdots && \vdots && \vdots\\ aV_{i1} & \cdots & aV_{ii} & \cdots & a^2V_{ii} + \dfrac{\alpha}{n} & \cdots & aV_{im}\\ \vdots && \vdots && \vdots && \vdots\\ V_{m1} & \cdots & V_{mi} & \cdots & aV_{mi} & \cdots & V_{mm} + \dfrac{\alpha}{n} \end{array} \right] \end{align*}

対角要素にαが加わることで、多重共線性が強い場合でも係数行列の行列式は正則となり、方程式は解を持つ。また正則化の効果より、αを大きな値とすることによって係数の値が小さく抑えられる。

行列による表示

式(3)の損失関数を、n個のデータに対する行列で表示すると以下の通り（重回帰の行列表現はこちらを参照）。

(11)   \begin{align*} L &= \left( \boldsymbol{Xw} - \boldsymbol{y} \right)^T \left( \boldsymbol{Xw} - \boldsymbol{y} \right) + \alpha \boldsymbol{w}^T \boldsymbol{w} \\ &= \boldsymbol{w}^T \boldsymbol{X}^T \boldsymbol{Xw} - 2\boldsymbol{y}^T \boldsymbol{Xw} + \boldsymbol{y}^T \boldsymbol{y} + \alpha \boldsymbol{w}^T \boldsymbol{w} \end{align*}

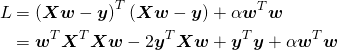
これをwで微分してLを最小とする値を求める。

(12)   \begin{gather*} \frac{dL}{d\boldsymbol{w}} = 2\boldsymbol{X}^T \boldsymbol{Xw} - 2 \boldsymbol{X}^T \boldsymbol{y} + 2 \alpha \boldsymbol{w} = \boldsymbol{0} \\ \boldsymbol{w} = \left( \boldsymbol{X}^T \boldsymbol{X} + \alpha \boldsymbol{I} \right)^{-1} \boldsymbol{X}^T \boldsymbol{y} \end{gather*}

 

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です