概要
sklearn.preprocessingモジュールのStandardScalerは、各特徴量の標本平均と標本分散を用いて特徴量を標準化する。
具体的には、特徴量Fiの標本平均(mi)と標本分散(vi)から以下の式により各特徴量FiをFi*に変換する。
(1) ![]()
挙動
それぞれ異なる正規分布に従う2つの特徴量について、StandardScalerを適用したときの挙動を以下に示す。異なる大きさとレンジの特徴量が、変換後には原点を中心としてほぼ同じような広がりになっているのがわかる。
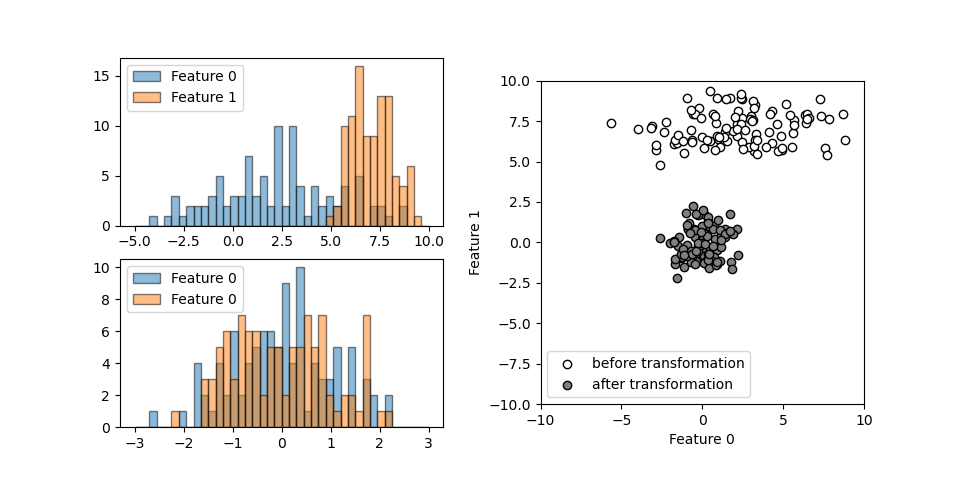
コードは以下の通りで、データに対してfit()メソッドでスケールパラメーターを決定し、transform()メソッドで変換を行うところを、これらを連続して実行するfit_transform()メソッドを使っている。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import numpy as np import numpy.random as rnd import matplotlib.pyplot as plt from sklearn.preprocessing import StandardScaler rnd.seed(0) x1 = rnd.normal(loc=2, scale=3, size=100) x2 = rnd.normal(loc=7, scale=1, size=100) X = np.hstack((x1.reshape(-1, 1), x2.reshape(-1, 1))) scaler = StandardScaler() X_transformed = scaler.fit_transform(X) fig = plt.figure(figsize=(9.6, 4.8)) fig.subplots_adjust(wspace=0.3) ax1 = fig.add_subplot(2, 2, 1) ax2 = fig.add_subplot(2, 2, 3) ax3 = fig.add_subplot(1, 2, 2) ax1.hist(X[:, 0], ec='k', range=(-5, 10), bins=40, alpha=0.5, label="Feature 0") ax1.hist(X[:, 1], ec='k', range=(-5, 10), bins=40, alpha=0.5, label="Feature 1") ax1.legend(loc='upper left') ax2.hist(X_transformed[:, 0], range=(-3, 3), bins=40, ec='k', alpha=0.5, label="Feature 0") ax2.hist(X_transformed[:, 1], range=(-3, 3), bins=40, ec='k', alpha=0.5, label="Feature 0") ax2.legend(loc='upper left') ax3.scatter(X[:, 0], X[:, 1], ec='k', fc='w', label="before transformation") ax3.scatter(X_transformed[:, 0], X_transformed[:, 1], ec='k', fc='gray', label="after transformation") ax3.set_aspect('equal') ax3.set_xlim(-10, 10) ax3.set_ylim(-10, 10) ax3.set_xlabel("Feature 0") ax3.set_ylabel("Feature 1") ax3.legend() plt.show() |
簡単なデータでStandardScalerの計算過程を確認しておく。以下の例では5個のデータにStandardScalerを適用している。これは1つの特徴量を持つ5個のデータを模していることになる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np from sklearn.preprocessing import StandardScaler x = np.array([1, 2, 3, 4, 5]) scaler = StandardScaler() x_transformed = scaler.fit_transform(x.reshape(-1, 1)) print(x_transformed.reshape(-1)) print("mean_ :{}".format(scaler.mean_)) print("var_ :{}".format(scaler.var_)) print("scale_:{}".format(scaler.scale_)) # [-1.41421356 -0.70710678 0. 0.70710678 1.41421356] # mean_ :[3.] # var_ :[2.] # scale_:[1.41421356] |
インスタンス内に保持されたパラメーターのうち、mean_は特徴量の標本平均、var_は標本分散(不偏分散ではない)となっている。scale_はvar_の平方根。
各データの特徴量は次式で標準化されているのが計算で確認できる。
(2) ![]()
特徴
StandardScalerは異常値の影響に対して比較的頑健である。