SVMの定式化

1 SVMの定式化

SVMのクラス分類の条件

2つの特徴量を持つデータが2つのクラスに分かれているとする。ここで下図のように、1つの直線によって、2つのクラスを完全に分離できるとする。

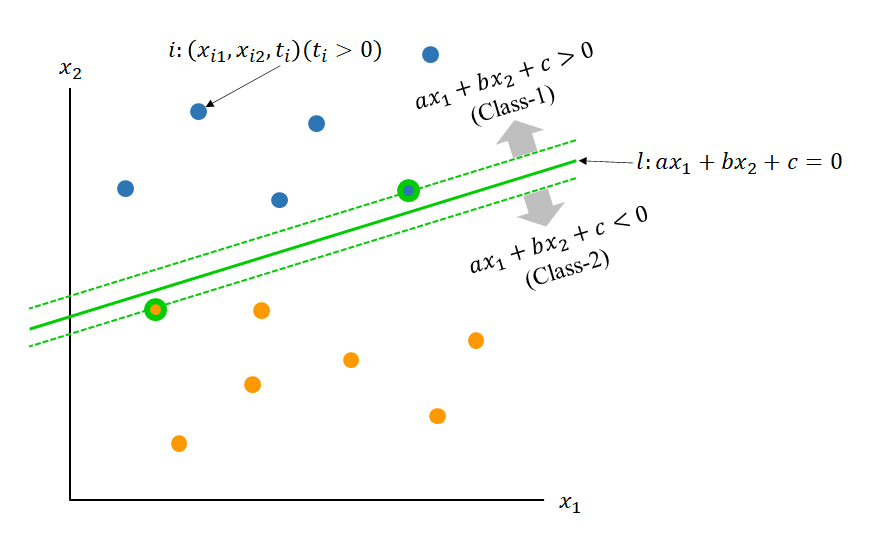
このとき、直線lによって分割したとして、以下の符号によってクラスを分離する。

(1) $\begin{equation*} \left\{ \begin{align} a x_1 + b x_2 + c > 0 &\rightarrow \rm{Class1} \\ a x_1 + b x_2 + c < 0 & \rightarrow \rm{Class2} \end{align} \right. \end{equation*}$

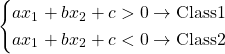
ここでラベル変数t_iを導入する。t_iはデータiがClass1/2のいずれに属するかを示す変数で、Class1ならt_i > 0、Class2ならt_i < 0と定義する。

(2) $\begin{equation*} \left\{ \begin{array}{lll} t_i = 1 & x_i \in \rm{Class1} & (a x_{i1} + b x_{i2} + c > 0) \\ t_i = -1 & x_i \in \rm{Class2} & (a x_{i1} + b x_{i2} + c < 0) \\ \end{array} \right. \end{equation*}$

このラベル変数を用いて、クラスの条件式は以下のように統一される。

(3) $\begin{equation*} t_i (a x_{i1} + b x_{i2} + c) > 0 \end{equation*}$

SVMにおいては、すべてのデータについてこの式が満足されるようにa, b, cを決定する。これらはすべてa, b, cに対する制約条件だが、どのようにこれらの値を求めるべきか、その目的関数が必要になる。SVMでは、これをマージン最大化により行う。

マージン最大化

ある直線l₁によって、下図のようにデータセットがClass1/2に分類できるとする。このときl₁に対してClass1/2の最も直線に近いデータを”サポートベクター”と呼ぶ。また、これらのサポートベクターに対応するl₁と平行な直線間の距離を”マージン”と呼ぶ。

ところで、l₁とは異なる別の直線l₂を選ぶと、異なるサポートベクターに対してより大きなマージンを得ることができる。SVMでは、式(3)のもとでこのマージンを最大化するような直線lを探すこととなる。

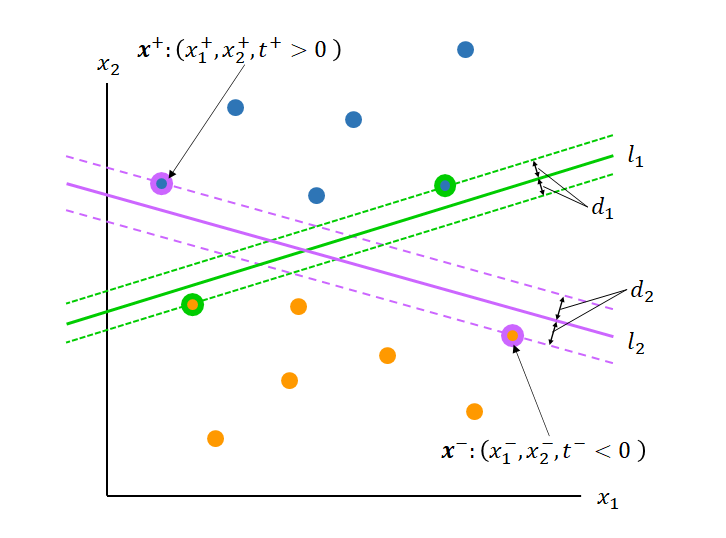
直線lに対するサポートベクターの対を(x⁺, x⁻)とすると、それぞれからlへの距離dは以下のように表現される。

(4) $\begin{equation*} d = \frac{|a x^+_1 + b x^+_2 + c|}{a^2 + b^2} = \frac{|a x^-_1 + b x^-_2 + c|}{a^2 + b^2} \end{equation*}$

ここで直線lはマージンの端にある平行な2つの直線の中央にあることから、上式の分子は同じ値となる。この値でdを除したものを改めて $\tilde{d}$ と置くと、dの最大化問題は $1/\tilde{d}=\sqrt{a^2+b^2}$ の最小化問題となる。これに式(3)の制約条件を加味して、問題は以下の制約条件付き最小化問題となる。

(5) $\begin{align*} \min a^2 + b^2 \quad {\rm s.t.} \; t_i (a x_{i1} + b x_{i2} + c) > 0 \; (i=1~n) \end{align*}$

今後の課題

ここから先の定式化
ソフトマージンの導出