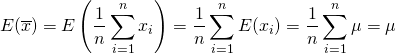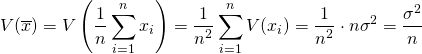概要
母集団から得られたサンプルから標本をつくり、それに対して統計的な検討を加える方法。限られたサンプルデータから異なる再標本を大量に作り(resampling)、母集団パラメーターの推定、アンサンブル機械学習のデータなどに用いる。
以下は、1次元配列に対してnumpy.random.choice()で並べ替えた再標本を複数生成している例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np np.random.seed(0) a = np.arange(10) for n in range(5): print(np.random.choice(a, len(a))) # [5 0 3 3 7 9 3 5 2 4] # [7 6 8 8 1 6 7 7 8 1] # [5 9 8 9 4 3 0 3 5 0] # [2 3 8 1 3 3 3 7 0 1] # [9 9 0 4 7 3 2 7 2 0] |
ブートストラップ(bootstrap)とはブーツの後ろについているつまみ/輪っかのことで、ここを持ったりフックをかけてブーツを引っ張り上げる。19世紀にはブートストラップを引っ張って自分自身を引っ張り上げる、という不可能なことの比喩に使われていたが、20世紀に入って自分自身で何とかすることや自己完結の仕組みなどの比喩に使われるようになったとのこと。コンピューターの起動を指すブートもbootstrapを略。
ブートストラップ法による信頼区間の推定
再標本を大量に生成することで、パラメーターの信頼区間などの統計量を直接得ることができる。
e-statの身長・体重に関する国民健康・栄養調査2017年のデータから、40歳代の日本国民の身長の平均171.2cm及び標準偏差6.0cmを母集団のパラメーターとして用いる(データ数は374人)。
このパラメーターから、正規分布に従う10個の乱数を発生させる。
|
1 |
180.9 167.5 168. 164.8 176.4 157.4 181.7 166.6 173.1 169.7 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats np.random.seed(1) pop_mean = 171.2 pop_std = 6 sample_size = 10 resample_size = sample_size n_boots = 1000 conf_prob = np.array([0.025, 0.975]) sample = np.random.normal(pop_mean, pop_std, sample_size) sample_mean = np.mean(sample) sample_uvar = np.var(sample, ddof=1) sample_std = np.sqrt(sample_uvar) |
次に、サンプルデータセットからブートストラップサンプリングで再標本を多数発生させ、それらの平均を一つのデータセットとする。
|
1 2 3 4 |
resample_means = [] for i in range(n_boots): resample = np.random.choice(sample, resample_size) resample_means.append(np.mean(resample)) |
numpy.percentile()で95 %信頼区間(2.5%~97.5%)を計算。
|
1 |
resample_conf = np.percentile(resample_means, conf_prob*100) |
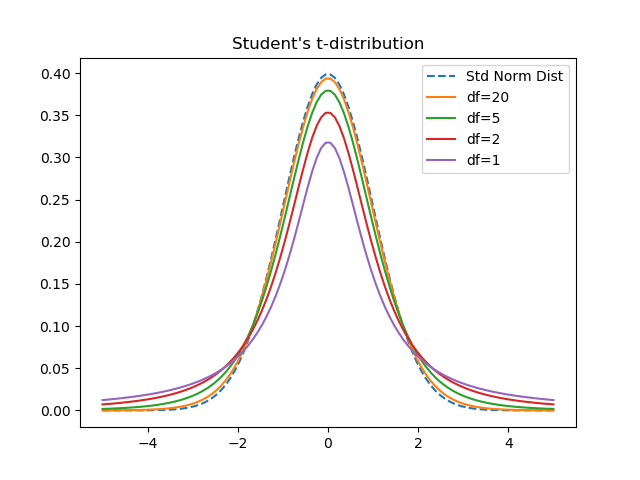
比較のため、元のサンプルについてt分布による平均の信頼区間も計算。scipy.stats.tのinterval()でも求められるが、ここでは愚直に元の計算式から計算した。
|
1 2 3 4 |
sample_conf = \ sample_mean + \ stats.t.ppf(conf_prob, df=sample_size-1) * \ np.sqrt(sample_uvar / sample_size) |
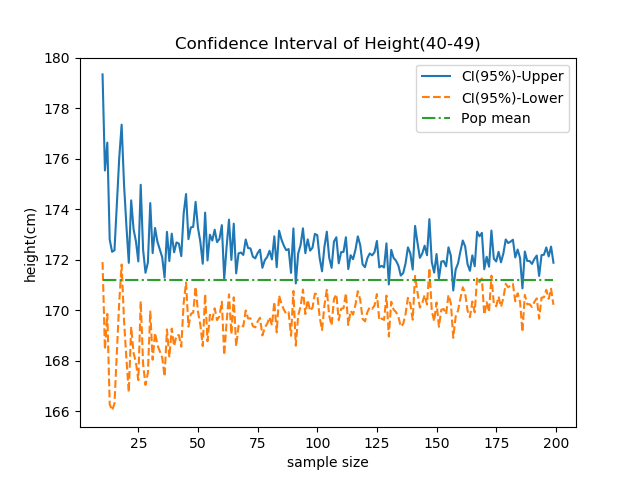
これらの結果、元の10個のサンプルの分布と1000個の再標本の平均の分布は以下のとおりで、釣り鐘状のきれいな分布となっている。
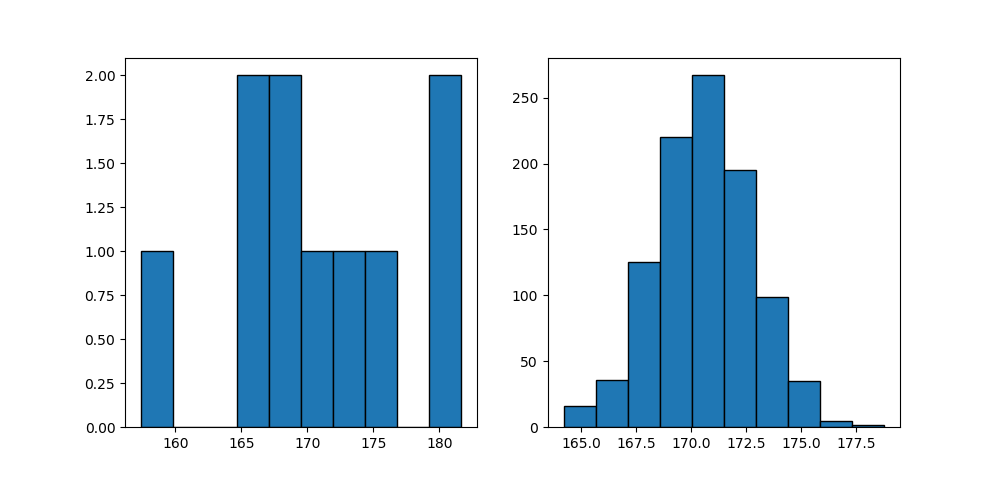
この時の各種データは以下の通り。
再標本の分散(不偏分散)は2.186と母集団やサンプルの分散より小さいが、これは多数の再標本の平均値の分散であり、母集団や元のサンプルの分散とは意味が違う。
また、10個のデータからt分布で推定した信頼区間よりも、ブートストラップで得られた信頼区間の方が狭くなっている。この傾向は乱数系列によって変わらず、一般的な傾向のようである。
|
1 2 3 4 5 6 7 |
Mean and STD population : 171.2, 6.000 sample : 170.6, 7.532 resample mean: 170.6, 2.186 Confidence interval sample : 165.23 - 176.01 (10.78) resample mean: 166.34 - 174.96 ( 8.62) |
以下は再標本数を1000から100にした場合だが、分布形状は整っていて信頼区間もt分布による推定より狭い。なお、再標本数を10万、100万と増やしても、これ以上分散は小さくならず、信頼区間も変化しない。
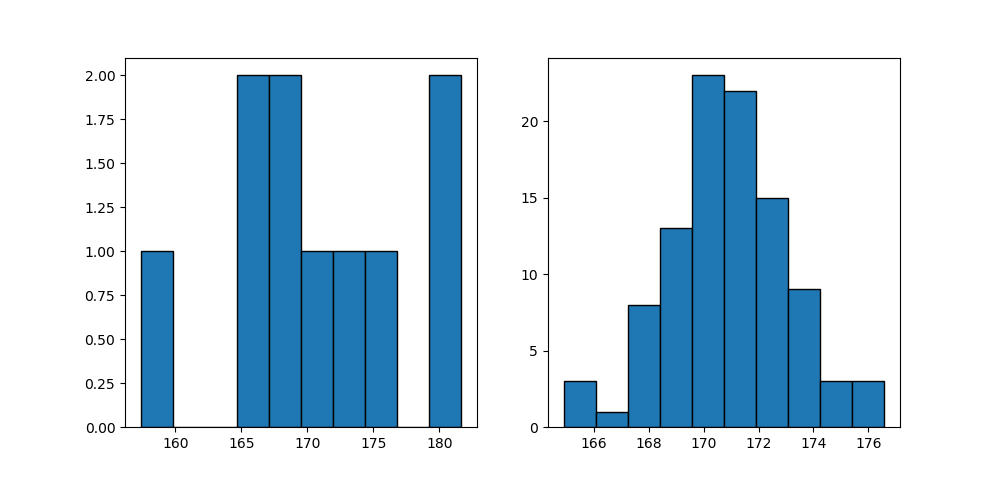
|
1 2 3 4 5 6 7 |
Mean and STD population : 171.2, 6.000 sample : 170.6, 7.532 resample mean: 170.9, 2.220 Confidence interval sample : 165.23 - 176.01 (10.78) resample mean: 166.21 - 175.32 ( 9.11) |
異常の計算・表示のコードは以下の通り。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats np.random.seed(1) pop_mean = 171.2 pop_std = 6 sample_size = 10 resample_size = sample_size n_boots = 1000 conf_prob = np.array([0.025, 0.975]) sample = np.random.normal(pop_mean, pop_std, sample_size) sample_mean = np.mean(sample) sample_uvar = np.var(sample, ddof=1) sample_std = np.sqrt(sample_uvar) resample_means = [] for i in range(n_boots): resample = np.random.choice(sample, resample_size) resample_means.append(np.mean(resample)) resample_means_mean = np.mean(resample_means) resample_means_std = np.sqrt(np.var(resample_means, ddof=1)) resample_conf = np.percentile(resample_means, conf_prob*100) sample_conf = \ sample_mean + \ stats.t.ppf(conf_prob, df=sample_size-1) * \ np.sqrt(sample_uvar / sample_size) print ("Mean and STD") print("population : {:5.1f}, {:5.3f}".format(pop_mean, pop_std)) print("sample : {:5.1f}, {:5.3f}".format(sample_mean, sample_std)) print("resample mean: {:5.1f}, {:5.3f}". format(resample_means_mean, resample_means_std)) print("Confidence interval") print("sample : {:6.2f} - {:6.2f} ({:5.2f})". format(sample_conf[0], sample_conf[1], sample_conf[1] - sample_conf[0])) print("resample mean: {:6.2f} - {:6.2f} ({:5.2f})". format(resample_conf[0], resample_conf[1], resample_conf[1] - resample_conf[0])) fig, axs = plt.subplots(1, 2, figsize=(10, 4.8)) axs[0].hist(sample, ec='k') axs[1].hist(resample_means, bins=10, ec='k') plt.show() |
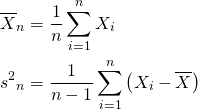
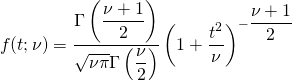
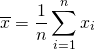
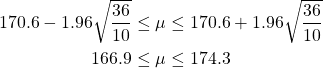
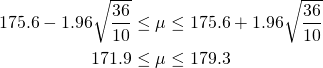
![Rendered by QuickLaTeX.com \begin{alignat*}{1} V(X) &= E(X^2) - [E(X)]^2 \\ &= \sum_{k=0}^n k^2 {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ &= \sum_{k=0}^n \left( k(k-1) + k \right) {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ &= \sum_{k=2}^n k(k-1) {}_n C_k p^k (1-p)^{n-k} + \sum_{k=1}^n k {}_n C_k p^k (1-p)^{n-k} - (np)^2 \\ \end{alignat*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-443e6acf6b414d16761dcd5f2a012a8d_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} r &=& \frac{{\rm Cov}(X, Y)}{\sqrt{V(X) \cdot V(Y)}} \\ &=& \frac{E(X - \overline{X})(Y - \overline{Y})} {\sqrt{ ( E\left[ (X - \overline{X})^2 \right] E\left[ (Y - \overline{Y})^2 \right] }} \\ &=& \frac{\displaystyle \sum_{i=1}^{n}(x_i - \overline{x})(y_i - \overline{y})} {\left[ \displaystyle \sum_{i=1}^{n} (x_i - \overline{x})^2 \displaystyle \sum_{i=1}^{n} (y_i - \overline{y})^2 \right]^{1/2}} \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-b9969ab54d441dc3797aad03fd503747_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} r &=& \frac{ {\rm Cov}(X, aX+b) } { \left[ V(X) \cdot V(aX+b) \right]^{1/2} } \\ &=& \frac{ a {\rm Cov}(X, X) } { \left[ V(X) \cdot a^2 V(X) \right]^{1/2} } \\ &=& \frac{a}{\sqrt{a^2}} \cdot \frac{ {\rm Cov}(X, X) } { \left[ V(X) \cdot V(X) \right]^{1/2} } \\ &=& \frac{a}{|a|} \cdot \frac{ V(X) } { V(X) } \\ &=& 1 \; {\rm or} \; -1 \end{eqnarray*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-0d7ce9a0442d3932b94aab482cf5e5d2_l3.png)