Lifegame Mobile (CoffeeScript)

2016-08-11 / tau / コメントする

初期パターン：

サイズ：
10　15　20　30　40

表示間隔：
0.1sec　0.2sec　0.5sec　1.0sec　1.5sec

Boids – 群の行動

2016-08-11 / tau / コメントする

動物の群の行動をシミュレートする”Boids”という考え方をCoffeeScriptで組んでみたもの。個体がそれぞれ独立して一定のルールに従って行動する結果、群としての整然とした行動をとるようになる。

スマートフォン用はこちら

個体数　　：
個体の速さ：
敵の数　　：
敵の速さ　：

Boidsの考え方や開発過程はこちら

このアプリケーションのコード説明はこちら

Boids 2.3 – コード説明

2016-08-11 / tau / コメントする

概要

Boids 2.3では、分離(Separation)、結合(Cohesion)に加えて「整列(Alignment)」のルールを導入する。整列行動の考え方は、ここでは以下の通りとした。

前方視野内に個体が存在する場合、それらの個体の平均速度を求める
進行方向を、群の平均速度の方へ向けて少し変更する

なおこのバージョンで、個体生成時にランダムに与える速度の計算方法を変更した。

速度計算の変更

これまで、個体を生成したときに与える速さは、上限値V_MAXを定数としておいて、V_MAX～VMAX/2の範囲で一様乱数を発生させていた。

  class Controler
    .....
    createCreature: ->
      .....
      v = (Math.random() + 1) * Creature._vMax / 2
      .....

class Controler

.....

createCreature: ->

.....

v = (Math.random() + 1) * Creature._vMax / 2

.....

Boids 2.3では、速さの上限値vMAXに加えて下限値vMINをCreatureクラスのクラス変数に持たせて、この間の一様乱数で速さを設定する。

  class Controler
    .....
    createCreature: ->
      .....
      v = Math.random() * (Creature._vMax - Creature._vMin) + Creature._vMin
      .....

class Controler

.....

createCreature: ->

.....

v = Math.random() * (Creature._vMax - Creature._vMin) + Creature._vMin

.....

これに伴って、以下を追加

HTMLの<script>要素に定数V_MINを追加
ControlerクラスにvMinのセッターを追加
セッターを通してV_MINの値をCreature._vMinにセット

  <script>
  //<![CDATA[
  BD23_V_MAX = 100;
  BD23_V_MIN = 0;
  .....
  //]]>
  </script>

//<![CDATA[

BD23_V_MAX = 100;

BD23_V_MIN = 0;

.....

//]]>

</script>

  class Controler
    .....
    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setVMin: (vMin) -> Creature._vMin = vMin
    .....

class Controler

.....

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setVMin: (vMin) -> Creature._vMin = vMin

.....

jQuery ($) ->
  .....
  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD23_V_MAX)
  controler.setVMin(BD23_V_MIN)
  .....

jQuery ($) ->

.....

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD23_V_MAX)

controler.setVMin(BD23_V_MIN)

.....

整列のアルゴリズム

平均速度の算出

次図において、先方視野内に個体が存在する場合、それらの平均速度v_meanを計算する。

${\bf v}_{\rm mean} = \frac{1}{n} \sum^n_{i=1} {\bf v}_i$

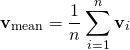
なお視野内の判定は、ベクトルの前後判定と個体との距離計算によっている。

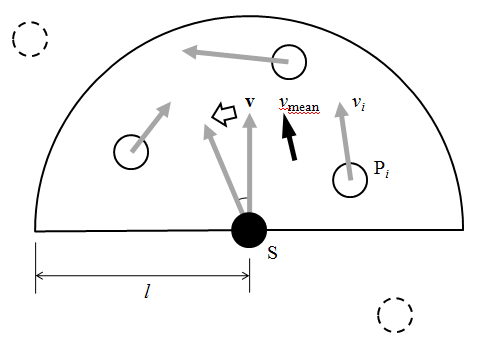
boid2x_alignment_vmean

進路変更

先の図のように、自身の進行方向に対する平均速度の方向によって、以下の手順で進路を変更する。

平均速度ベクトルの向きが自身の進行方向より左右どちらに向いているかを判定
平均速度ベクトルが進行方向より右に向いているなら右へ、左に向いているなら左へ方向を少し変化させる。

これらの考え方はBoids 2.1の分離行動における回避動作と同じ。

コード内容

初期パラメータ定義

HTMLで定義する初期パラメータに、整列に関する以下の変数を追加する。

整列判定の視野の深さ(BD23_ALIGNMENT_FIELD_DEPTH)
整列行動における速度の変更角(BD23_ALIGNMENT_ANGLE)

なお、このバージョンで分離行動の視野の深さの変数名を変更している。

  <script>
  //<![CDATA[
  BD23_V_MAX = 100;
  BD23_V_MIN = 0;
  BD23_CREATURE_SIZE = 10;
  BD23_WALL_DETECTION_LENGTH = 100;
  BD23_WALL_REPULSION_PARAM = 16;
  // boIDS2.3で名前変更：分離行動の視野の深さ
  BD23_SEPARATION_FIELD_DEPTH = 50;
  BD23_SEPARATION_ANGLE = 10 * Math.PI / 180;
  BD23_COHESION_ANGLE = 5 * Math.PI / 180;
  // Boids 2.3で追加：整列行動の視野の深さと速度変更角
  BD23_ALIGNMENT_FIELD_DEPTH = 250;
  BD23_ALIGNMENT_ANGLE = 5 * Math.PI / 180;
  BD23_INTERVAL_SEC = 0.05;
  //]]>
  </script>

//<![CDATA[

BD23_V_MAX = 100;

BD23_V_MIN = 0;

BD23_CREATURE_SIZE = 10;

BD23_WALL_DETECTION_LENGTH = 100;

BD23_WALL_REPULSION_PARAM = 16;

// boIDS2.3で名前変更：分離行動の視野の深さ

BD23_SEPARATION_FIELD_DEPTH = 50;

BD23_SEPARATION_ANGLE = 10 * Math.PI / 180;

BD23_COHESION_ANGLE = 5 * Math.PI / 180;

// Boids 2.3で追加：整列行動の視野の深さと速度変更角

BD23_ALIGNMENT_FIELD_DEPTH = 250;

BD23_ALIGNMENT_ANGLE = 5 * Math.PI / 180;

BD23_INTERVAL_SEC = 0.05;

//]]>

</script>

クラス変数

初期パラメータの保存のため、Creatureクラスのクラス変数を追加する。

  class Creature extends MovingAgent
    # private ｓtaticなクラス・プロパティ
    # ランダムに速度を発生させるときの最大速度と最小速度
    @_vMax: 100
    @_vMin: 50
    # 描画の基本となるサイズ
    @_drawSize: 8
    # 壁の衝突回避を認識する距離
    @_wallDetectionLength:  100
    # 反発力パラメータ
    @_wallRepulsionParam: 4
    # 視野の長さ(奥行)
    @_separationFieldDepth: 100
    # 分離行動の回避角
    @_separationAngle: 0
    # 結合行動の回避角
    @_cohesionAngle: 0
    # 整列高度の視野の長さ(奥行)
    @_alignmentFieldDepth: 100
    # 整列行動の変化角
    @_alignmentAngle: 0
    .....

class Creature extends MovingAgent

# private ｓtaticなクラス・プロパティ

# ランダムに速度を発生させるときの最大速度と最小速度

@_vMax: 100

@_vMin: 50

# 描画の基本となるサイズ

@_drawSize: 8

# 壁の衝突回避を認識する距離

@_wallDetectionLength: 100

# 反発力パラメータ

@_wallRepulsionParam: 4

# 視野の長さ(奥行)

@_separationFieldDepth: 100

# 分離行動の回避角

@_separationAngle: 0

# 結合行動の回避角

@_cohesionAngle: 0

# 整列高度の視野の長さ(奥行)

@_alignmentFieldDepth: 100

# 整列行動の変化角

@_alignmentAngle: 0

.....

パラメータのセッター

Controlerクラスに、Creatureクラス変数へのセッターを定義する。

  class Controler
    .....
    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setVMin: (vMin) -> Creature._vMin = vMin
    setCreatureSize: (size) -> Creature._drawSize = size
    setWallDetectionLength: (pix) -> Creature._wallDetectionLength =  pix
    setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param
    setSeparationFieldDepth: (length) -> Creature._separationFieldDepth = length
    setSeparationAngle: (angle) -> Creature._separationAngle = angle
    setCohesionAngle: (angle) -> Creature._cohesionAngle = angle
    setAlignmentFieldDepth: (length) -> Creature._alignmentFieldDepth = length
    setAlignmentAngle: (angle) -> Creature._alignmentAngle = angle
    setIntervalSec: (@interval_sec) ->
    .....

class Controler

.....

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setVMin: (vMin) -> Creature._vMin = vMin

setCreatureSize: (size) -> Creature._drawSize = size

setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix

setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param

setSeparationFieldDepth: (length) -> Creature._separationFieldDepth = length

setSeparationAngle: (angle) -> Creature._separationAngle = angle

setCohesionAngle: (angle) -> Creature._cohesionAngle = angle

setAlignmentFieldDepth: (length) -> Creature._alignmentFieldDepth = length

setAlignmentAngle: (angle) -> Creature._alignmentAngle = angle

setIntervalSec: (@interval_sec) ->

.....

パラメータのセット

HTMLで定義されたパラメータをControlerオブジェクトのセッターによってセットする。

# スクリプトが読み込まれた時の実行部分
jQuery ($) ->
  # Controlerを作成し、canvasオブジェクトを渡す
  canvas = $("#Boids23_canvas")[0]
  controler = new Boids23.Controler(canvas)
  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD23_V_MAX)
  controler.setVMin(BD23_V_MIN)
  controler.setCreatureSize(BD23_CREATURE_SIZE)
  controler.setWallDetectionLength(BD23_WALL_DETECTION_LENGTH)
  controler.setWallRepulsionParam(BD23_WALL_REPULSION_PARAM)
  controler.setSeparationFieldDepth(BD23_SEPARATION_FIELD_DEPTH)
  controler.setSeparationAngle(BD23_SEPARATION_ANGLE)
  controler.setCohesionAngle(BD23_COHESION_ANGLE)
  controler.setAlignmentFieldDepth(BD23_ALIGNMENT_FIELD_DEPTH)
  controler.setAlignmentAngle(BD23_ALIGNMENT_ANGLE)
  controler.setIntervalSec(BD23_INTERVAL_SEC)
  .....

# スクリプトが読み込まれた時の実行部分

jQuery ($) ->

# Controlerを作成し、canvasオブジェクトを渡す

canvas = $("#Boids23_canvas")[0]

controler = new Boids23.Controler(canvas)

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD23_V_MAX)

controler.setVMin(BD23_V_MIN)

controler.setCreatureSize(BD23_CREATURE_SIZE)

controler.setWallDetectionLength(BD23_WALL_DETECTION_LENGTH)

controler.setWallRepulsionParam(BD23_WALL_REPULSION_PARAM)

controler.setSeparationFieldDepth(BD23_SEPARATION_FIELD_DEPTH)

controler.setSeparationAngle(BD23_SEPARATION_ANGLE)

controler.setCohesionAngle(BD23_COHESION_ANGLE)

controler.setAlignmentFieldDepth(BD23_ALIGNMENT_FIELD_DEPTH)

controler.setAlignmentAngle(BD23_ALIGNMENT_ANGLE)

controler.setIntervalSec(BD23_INTERVAL_SEC)

.....

Ceatureクラスの変更 – alignment()メソッドの追加

Creatureクラスのmove()メソッドがalignment()メソッドを呼び出すようにする。

  class Creature extends MovingAgent

    .....

    move: (interval_sec) ->
      # 壁を避ける
      @wallAvoidance()

      # 分離行動(separation)
      @separation()

      # 結合行動(cohesion)
      @cohesion()

      # 整列行動(alignment)
      @alignment()

      .....

class Creature extends MovingAgent

.....

move: (interval_sec) ->

# 壁を避ける

@wallAvoidance()

# 分離行動(separation)

@separation()

# 結合行動(cohesion)

@cohesion()

# 整列行動(alignment)

@alignment()

.....

alignment()メソッドを新たに定義する。

速度の方向を変化させる回転行列のcos、sinに対応したローカル変数cs、snを定義している
平均速度の参照がvMeanプロパティに保存されるが、視野内に個体が存在しないときはnullとなる
速度の回転方向は、右がマイナス方向、左がプラス方向となることに注意

    # Boids2.3
    # 整列行動(alignment)
    # 分離行動と同じ視野内の個体群の平均速度に合わせるよう速度の方向を変更
    alignment: ->
      # 平均速度計算用
      vMean = null
      n = 0
      # 整列行動の方向転換計算用cos/sin
      cs = Math.cos(Creature._alignmentAngle)
      sn = Math.sin(Creature._alignmentAngle)

      # 自分以外の群のすべての個体についてサーチ
      for other in @cluster.creatures
        if other != this
          # その個体が自分の前方にいるなら
          if other.isInFrontOf(this)
            d = Vector.distance(this.pos, other.pos)
            # その個体が視野の中にいるなら
            if d <= Creature._alignmentFieldDepth
              # 既に個体が視野内にあれば平均速度の計算を続行
              n++
              if vMean?
                vMean.plusEq(other.v)
              else
                vMean = new Vector(0, 0)
      # 視野内に個体がいたなら速度変更の計算へ
      if vMean?
        vMean.divEq(n)
        ###
        @v.plusEq(vMean)
        newV = @v.abs()
        if newV >= Creature._vMax
          @v.timesEq(vMean.abs() / newV)
        ###
        if vMean.isHeadingToRightOf(@v)
          vx =  @v.x * cs + @v.y * sn
          vy = -@v.x * sn + @v.y * cs
        else
          vx = @v.x * cs - @v.y * sn
          vy = @v.x * sn + @v.y * cs
        @v.x = vx
        @v.y = vy

# Boids2.3

# 整列行動(alignment)

# 分離行動と同じ視野内の個体群の平均速度に合わせるよう速度の方向を変更

alignment: ->

# 平均速度計算用

vMean = null

n = 0

# 整列行動の方向転換計算用cos/sin

cs = Math.cos(Creature._alignmentAngle)

sn = Math.sin(Creature._alignmentAngle)

# 自分以外の群のすべての個体についてサーチ

for other in @cluster.creatures

if other != this

# その個体が自分の前方にいるなら

if other.isInFrontOf(this)

d = Vector.distance(this.pos, other.pos)

# その個体が視野の中にいるなら

if d <= Creature._alignmentFieldDepth

# 既に個体が視野内にあれば平均速度の計算を続行

n++

if vMean?

vMean.plusEq(other.v)

else

vMean = new Vector(0, 0)

# 視野内に個体がいたなら速度変更の計算へ

if vMean?

vMean.divEq(n)

###

@v.plusEq(vMean)

newV = @v.abs()

if newV >= Creature._vMax

@v.timesEq(vMean.abs() / newV)

###

if vMean.isHeadingToRightOf(@v)

vx = @v.x * cs + @v.y * sn

vy = -@v.x * sn + @v.y * cs

else

vx = @v.x * cs - @v.y * sn

vy = @v.x * sn + @v.y * cs

@v.x = vx

@v.y = vy

全コード

以下に、分離、結合、整列の3ルールすべてを適用したBoids 2.3の全コードを示す。

# Boids 2.3
# Boids 2.2に整列行動(alignment)を加える
Boids23 = {}

# パッケージBoids23の本体
do ->
  # 独自クラスのエイリアス
  # パッケージtaustation_geom2d.jsが必要。
  Vector = taustation_geom2d.Vector
  MovingAgent = taustation_geom2d.MovingAgent

  # Boidsが活動する空間のクラス
  # このバージョンでは、canvasオブジェクトの上下左右の座標を持つ長方形
  class Field
    constructor: (canvas) ->
      @xMin = 0
      @yMin = 0
      @xMax = canvas.width
      @yMax = canvas.height


  # Boidsの個体を実現するクラス
  # 位置座標と速度ベクトルの成分を保持する
  # 自らが活動するFieldクラスのオブジェクトへの参照も保持する
  class Creature extends MovingAgent
    # private ｓtaticなクラス・プロパティ
    # ランダムに速度を発生させるときの最大速度と最小速度
    @_vMax: 100
    @_vMin: 50
    # 描画の基本となるサイズ
    @_drawSize: 8
    # 壁の衝突回避を認識する距離
    @_wallDetectionLength:  100
    # 反発力パラメータ
    @_wallRepulsionParam: 4
    # 視野の長さ(奥行)
    @_separationFieldDepth: 100
    # 分離行動の回避角
    @_separationAngle: 0
    # 結合行動の回避角
    @_cohesionAngle: 0
    # 整列高度の視野の長さ(奥行)
    @_alignmentFieldDepth: 100
    # 整列行動の変化角
    @_alignmentAngle: 0

    # コンストラクタの引数にはFieldオブジェクトを渡す
    # 位置、速度、加速度、自分が属する群、Fieldをプロパティとして持つ
    constructor: (cluster, field) ->
      super()
      @a = new Vector(0, 0)
      @cluster = cluster
      @field = field
      @nearestCreature = null

    # 個体を描画するメソッド
    # canvasのコンテキストを引数で受け取る
    draw: (ctx) ->
      v = @v.abs()
      sx = Creature._drawSize * @v.x / v
      sy = Creature._drawSize * @v.y / v
      p = 0.25

      ctx.fillStyle = "black"
      ctx.beginPath()
      ctx.moveTo(@pos.x + (1 - p) * sx, @pos.y + (1 - p) * sy)
      ctx.lineTo(@pos.x + (-sx - sy) * p, @pos.y + (sx - sy) * p)
      ctx.lineTo(@pos.x + (-sx + sy) * p, @pos.y + (-sx - sy) * p)
      ctx.closePath()
      ctx.fill()
      return

    # 個体を動かすメソッド
    # 「群れ」を表すClusterクラスのmove()メソッドから呼ばれる
    # interval_secは秒単位のアニメーション・フレームのインターバル
    move: (interval_sec) ->
      # 壁を避ける
      @wallAvoidance()

      # 分離行動(separation)
      @separation()

      # 結合行動(cohesion)
      @cohesion()

      # 整列行動(alignment)
      @alignment()

      # 加速度を考慮した速度の変化を計算
      # 速度の絶対値が増え続けないようにキャップで抑える
      # 速度成分の符号を得るのに、Math.signがサポートされていないブラウザが多いため、
      # 値/絶対値で符号を得ている
      @v.plusEq(@a.times interval_sec)
      @v.x = @v.x / Math.abs(@v.x) * Math.min(Math.abs(@v.x), Creature._vMax)
      @v.y = @v.y / Math.abs(@v.y) * Math.min(Math.abs(@v.y), Creature._vMax)

      # インターバルの間の移動量を計算
      @pos.plusEq(@v.times interval_sec)

      # 壁にぶつかった場合は全反射
      if @pos.x <= @field.xMin
        @pos.x = @field.xMin * 2 - @pos.x
        @v.x = -@v.x
      else if @pos.x >= @field.xMax
        @pos.x = @field.xMax * 2 - @pos.x
        @v.x = -@v.x
      if @pos.y <= @field.yMin
        @pos.y = @field.yMin * 2 - @pos.y
        @v.y = -@v.y
      else if @pos.y >= @field.yMax
        @pos.y = @field.yMax * 2 - @pos.y
        @v.y = -@v.y

      return

    # 壁を避ける行動
    # 壁からの距離に応じた斥力を(repulsion)想定し、ｘ/ｙ方向の加速度を計算
    wallAvoidance: ->
      if @pos.x <= Creature._wallDetectionLength
        @a.x =
          Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / @pos.x) ** 2
      else if @pos.x >= @field.xMax - Creature._wallDetectionLength
        @a.x =
          -Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / (@field.xMax - @pos.x)) ** 2
      else
        @a.x = 0

      if @pos.y <= Creature._wallDetectionLength
        @a.y =
          Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / @pos.y) ** 2
      else if @pos.y >= @field.yMax - Creature._wallDetectionLength
        @a.y =
          -Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / (@field.yMax - @pos.y)) ** 2
      else
        @a.y = 0

    # Boids2.1
    # 分離行動(separation)
    # 前方視角180度内で一定距離内の視野の中で、最も近い個体を避ける
    # 相手方の速度の向きには関係なく、相手側と反対方向に速度の向きをを少し変更する。
    separation: ->
      # 回避行動の方向転換計算用cos/sin
      cs = Math.cos(Creature._separationAngle)
      sn = Math.sin(Creature._separationAngle)
      # 自身に最も近い個体
      @nearestCreature = null

      # 自分以外の群のすべての個体についてサーチ
      for other in @cluster.creatures
        if other != this
          # その個体が自分の前方にいるなら
          if other.isInFrontOf(this)
            d = Vector.distance(this.pos, other.pos)
            # その個体が視野の中にいるなら
            if d <= Creature._separationFieldDepth
              # 周世に個体がセットされていて、今回の個体の方が近ければ入れ替え
              # 最初に認識した個体ならそのままセット
              if @nearestCreature?
                if d <= Vector.distance(@nearestCreature.pos, this.pos)
                  @nearestCreature = other
              else
                @nearestCreature = other
      # 近くの個体が視野内に存在するなら回避計算
      if @nearestCreature?
        # 相手が自分の右にいるなら左へ、自分の左にいるなら右へ向きを変更
        if @nearestCreature.isOnTheRightOf(this)
          vx = @v.x * cs - @v.y * sn
          vy = @v.x * sn + @v.y * cs
        else
          vx =  @v.x * cs + @v.y * sn
          vy = -@v.x * sn + @v.y * cs
        @v.x = vx
        @v.y = vy

    # Boids2.2
    # 結合行動(cohesion)
    # 前方視角180度以内の全個体の重心に向かって速度を少し変更する
    cohesion: ->
      # 群のうち認識した個体の数とそのグループの重心
      n = 0
      clusterCenter = null
      # 結合行動の方向転換計算用cos/sin
      cs = Math.cos(Creature._cohesionAngle)
      sn = Math.sin(Creature._cohesionAngle)

      # 自分以外の群のすべての個体についてサーチ
      for other in @cluster.creatures
        if other != this
          # 相手が自身の前方にいるなら、その位置を考慮
          if other.isInFrontOf(this)
            n++
            if clusterCenter?
              clusterCenter.plusEq(other.pos)
            else
              clusterCenter = new Vector(other.pos.x, other.pos.y)

      # 前方の相手が1つでも存在すれば、結合行動をとる
      if clusterCenter?
        clusterCenter.divEq(n)
        # 重心が自分の右にあれば左に、自分の左にあれば右に進路を変更
        if clusterCenter.isOnTheRightOf(this)
          vx =  @v.x * cs + @v.y * sn
          vy = -@v.x * sn + @v.y * cs
        else
          vx = @v.x * cs - @v.y * sn
          vy = @v.x * sn + @v.y * cs
        @v.x = vx
        @v.y = vy

    # Boids2.3
    # 整列行動(alignment)
    # 分離行動と同じ視野内の個体群の平均速度に合わせるよう速度の方向を変更
    alignment: ->
      # 平均速度計算用
      vMean = null
      n = 0
      # 整列行動の方向転換計算用cos/sin
      cs = Math.cos(Creature._alignmentAngle)
      sn = Math.sin(Creature._alignmentAngle)

      # 自分以外の群のすべての個体についてサーチ
      for other in @cluster.creatures
        if other != this
          # その個体が自分の前方にいるなら
          if other.isInFrontOf(this)
            d = Vector.distance(this.pos, other.pos)
            # その個体が視野の中にいるなら
            if d <= Creature._alignmentFieldDepth
              # 既に個体が視野内にあれば平均速度の計算を続行
              n++
              if vMean?
                vMean.plusEq(other.v)
              else
                vMean = new Vector(0, 0)
      # 視野内に個体がいたなら速度変更の計算へ
      if vMean?
        vMean.divEq(n)
        ###
        @v.plusEq(vMean)
        newV = @v.abs()
        if newV >= Creature._vMax
          @v.timesEq(vMean.abs() / newV)
        ###
        if vMean.isHeadingToRightOf(@v)
          vx =  @v.x * cs + @v.y * sn
          vy = -@v.x * sn + @v.y * cs
        else
          vx = @v.x * cs - @v.y * sn
          vy = @v.x * sn + @v.y * cs
        @v.x = vx
        @v.y = vy


  # Boidsの群を管理するクラスで、以下を保持する
  # ・群を構成する複数の個体
  # ・個体を描画するcanvasとそのcontextのオブジェクト
  class Cluster
    # コンストラクタはcanvasオブジェクトを受け取り、そのcontextをプロパティに登録
    constructor: (canvas) ->
      @creatures = []
      @canvas = canvas
      @context = @canvas.getContext("2d") if @canvas.getContext
      return

    # すべての個体オブジェクトを群から削除する
    clearCreatures: ->
      @creatures = []

    # 引数で与えられた個体を群に加える
    addCreature: (creature) ->
      @creatures.push(creature)
      return

    # 群の全個体を描画する
    # 描画エリアをクリアした後、群の全個体のdraw()メソッドを呼び出している
    draw: ->
      @context.fillStyle = "#e0e0e0"
      @context.fillRect(0, 0, @canvas.width, @canvas.height)
      for creature in @creatures
        creature.draw(@context)
      return

    # 秒単位のインターバル受け取り、すべての個体を移動させる
    move: (interval_sec) ->
      for creature in @creatures
        creature.move(interval_sec)
      return


  # Boidsアプリケーションの動作を統括するクラス
  # 唯一、ブラウザから直接呼び出され、初期値の設定やClusterの操作を担当
  class Controler
    # Boids 1.2からstaticなクラスプロパティとした
    @interval_sec: 1 # animation frame interval in seconds

    constructor: (canvas) ->
      # Boidsの活動領域
      @field = new Field(canvas)
      # 群のオブジェクト
      @cluster = new Cluster(canvas)
      # 個体の数
      @population = 0
      # アニメーション用のフラグとtimer
      @isRunning = false
      @timer = undefined

    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setVMin: (vMin) -> Creature._vMin = vMin
    setCreatureSize: (size) -> Creature._drawSize = size
    setWallDetectionLength: (pix) -> Creature._wallDetectionLength =  pix
    setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param
    setSeparationFieldDepth: (length) -> Creature._separationFieldDepth = length
    setSeparationAngle: (angle) -> Creature._separationAngle = angle
    setCohesionAngle: (angle) -> Creature._cohesionAngle = angle
    setAlignmentFieldDepth: (length) -> Creature._alignmentFieldDepth = length
    setAlignmentAngle: (angle) -> Creature._alignmentAngle = angle
    setIntervalSec: (@interval_sec) ->

    # 一つの個体を発生させるメソッド
    # 位置はcanvasに収まるよう、速度はvMax/2～vMaxの範囲でランダム
    createCreature: ->
      cr = new Creature(@cluster, @field)
      x = Math.floor(Math.random() * @field.xMax)
      y = Math.floor(Math.random() * @field.yMax)
      v = Math.random() * (Creature._vMax - Creature._vMin) + Creature._vMin
      a = Math.random() * Math.PI * 2
      cr.setPosition(x, y)
      cr.setVelocity(v * Math.cos(a), v * Math.sin(a))
      return cr

    # 引数で指定された数の個体を発生させ、Clusterオブジェクトに登録する
    generate: (@population) ->
      @cluster.clearCreatures()
      for i in [1..@population]
        cr = @createCreature()
        @cluster.addCreature(cr)
      @cluster.draw()

    # アニメーションの開始／停止の切り替え
    # アニメーションはsetInterval()で実装している
    startAndStop: () ->
      if @isRunning
        clearInterval(@timer)
        @isRunning = false
      else
        @timer = setInterval =>
          @cluster.move(@interval_sec)
          @cluster.draw()
          return
        , @interval_sec * 1000
        @isRunning = true
      return

  # 外部からアクセス可能な名前の設定
  Boids23.Controler = Controler


# スクリプトが読み込まれた時の実行部分
jQuery ($) ->
  # Controlerを作成し、canvasオブジェクトを渡す
  canvas = $("#Boids23_canvas")[0]
  controler = new Boids23.Controler(canvas)
  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD23_V_MAX)
  controler.setVMin(BD23_V_MIN)
  controler.setCreatureSize(BD23_CREATURE_SIZE)
  controler.setWallDetectionLength(BD23_WALL_DETECTION_LENGTH)
  controler.setWallRepulsionParam(BD23_WALL_REPULSION_PARAM)
  controler.setSeparationFieldDepth(BD23_SEPARATION_FIELD_DEPTH)
  controler.setSeparationAngle(BD23_SEPARATION_ANGLE)
  controler.setCohesionAngle(BD23_COHESION_ANGLE)
  controler.setAlignmentFieldDepth(BD23_ALIGNMENT_FIELD_DEPTH)
  controler.setAlignmentAngle(BD23_ALIGNMENT_ANGLE)
  controler.setIntervalSec(BD23_INTERVAL_SEC)

  # Generateボタンが押されたとき、指定された個体数で群をつくる
  $("#boids23_generate").click ->
    pop = $("#boids23_population").val()
    if pop < 1
      pop = 1
      $("#boids23_population").val(pop)
    controler.generate(pop)

  # Start/Stopボタンが押されたとき、アニメーションの動作を切り替える
  $("#boids23_start_and_stop").click ->
    controler.startAndStop()

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

289

290

291

292

293

294

295

296

297

298

299

300

301

302

303

304

305

306

307

308

309

310

311

312

313

314

315

316

317

318

319

320

321

322

323

324

325

326

327

328

329

330

331

332

333

334

335

336

337

338

339

340

341

342

343

344

345

346

347

348

349

350

351

352

353

354

355

356

357

358

359

360

361

362

363

364

365

366

367

368

369

370

371

372

373

374

375

376

377

378

379

380

381

382

383

384

385

386

387

388

389

390

391

392

# Boids 2.3

# Boids 2.2に整列行動(alignment)を加える

Boids23 = {}

# パッケージBoids23の本体

do ->

# 独自クラスのエイリアス

# パッケージtaustation_geom2d.jsが必要。

Vector = taustation_geom2d.Vector

MovingAgent = taustation_geom2d.MovingAgent

# Boidsが活動する空間のクラス

# このバージョンでは、canvasオブジェクトの上下左右の座標を持つ長方形

class Field

constructor: (canvas) ->

@xMin = 0

@yMin = 0

@xMax = canvas.width

@yMax = canvas.height

# Boidsの個体を実現するクラス

# 位置座標と速度ベクトルの成分を保持する

# 自らが活動するFieldクラスのオブジェクトへの参照も保持する

class Creature extends MovingAgent

# private ｓtaticなクラス・プロパティ

# ランダムに速度を発生させるときの最大速度と最小速度

@_vMax: 100

@_vMin: 50

# 描画の基本となるサイズ

@_drawSize: 8

# 壁の衝突回避を認識する距離

@_wallDetectionLength: 100

# 反発力パラメータ

@_wallRepulsionParam: 4

# 視野の長さ(奥行)

@_separationFieldDepth: 100

# 分離行動の回避角

@_separationAngle: 0

# 結合行動の回避角

@_cohesionAngle: 0

# 整列高度の視野の長さ(奥行)

@_alignmentFieldDepth: 100

# 整列行動の変化角

@_alignmentAngle: 0

# コンストラクタの引数にはFieldオブジェクトを渡す

# 位置、速度、加速度、自分が属する群、Fieldをプロパティとして持つ

constructor: (cluster, field) ->

super()

@a = new Vector(0, 0)

@cluster = cluster

@field = field

@nearestCreature = null

# 個体を描画するメソッド

# canvasのコンテキストを引数で受け取る

draw: (ctx) ->

v = @v.abs()

sx = Creature._drawSize * @v.x / v

sy = Creature._drawSize * @v.y / v

p = 0.25

ctx.fillStyle = "black"

ctx.beginPath()

ctx.moveTo(@pos.x + (1 - p) * sx, @pos.y + (1 - p) * sy)

ctx.lineTo(@pos.x + (-sx - sy) * p, @pos.y + (sx - sy) * p)

ctx.lineTo(@pos.x + (-sx + sy) * p, @pos.y + (-sx - sy) * p)

ctx.closePath()

ctx.fill()

return

# 個体を動かすメソッド

# 「群れ」を表すClusterクラスのmove()メソッドから呼ばれる

# interval_secは秒単位のアニメーション・フレームのインターバル

move: (interval_sec) ->

# 壁を避ける

@wallAvoidance()

# 分離行動(separation)

@separation()

# 結合行動(cohesion)

@cohesion()

# 整列行動(alignment)

@alignment()

# 加速度を考慮した速度の変化を計算

# 速度の絶対値が増え続けないようにキャップで抑える

# 速度成分の符号を得るのに、Math.signがサポートされていないブラウザが多いため、

# 値/絶対値で符号を得ている

@v.plusEq(@a.times interval_sec)

@v.x = @v.x / Math.abs(@v.x) * Math.min(Math.abs(@v.x), Creature._vMax)

@v.y = @v.y / Math.abs(@v.y) * Math.min(Math.abs(@v.y), Creature._vMax)

# インターバルの間の移動量を計算

@pos.plusEq(@v.times interval_sec)

# 壁にぶつかった場合は全反射

if @pos.x <= @field.xMin

@pos.x = @field.xMin * 2 - @pos.x

@v.x = -@v.x

else if @pos.x >= @field.xMax

@pos.x = @field.xMax * 2 - @pos.x

@v.x = -@v.x

if @pos.y <= @field.yMin

@pos.y = @field.yMin * 2 - @pos.y

@v.y = -@v.y

else if @pos.y >= @field.yMax

@pos.y = @field.yMax * 2 - @pos.y

@v.y = -@v.y

return

# 壁を避ける行動

# 壁からの距離に応じた斥力を(repulsion)想定し、ｘ/ｙ方向の加速度を計算

wallAvoidance: ->

if @pos.x <= Creature._wallDetectionLength

@a.x =

Creature._wallRepulsionParam *

(Creature._wallDetectionLength / @pos.x) ** 2

else if @pos.x >= @field.xMax - Creature._wallDetectionLength

@a.x =

-Creature._wallRepulsionParam *

(Creature._wallDetectionLength / (@field.xMax - @pos.x)) ** 2

else

@a.x = 0

if @pos.y <= Creature._wallDetectionLength

@a.y =

Creature._wallRepulsionParam *

(Creature._wallDetectionLength / @pos.y) ** 2

else if @pos.y >= @field.yMax - Creature._wallDetectionLength

@a.y =

-Creature._wallRepulsionParam *

(Creature._wallDetectionLength / (@field.yMax - @pos.y)) ** 2

else

@a.y = 0

# Boids2.1

# 分離行動(separation)

# 前方視角180度内で一定距離内の視野の中で、最も近い個体を避ける

# 相手方の速度の向きには関係なく、相手側と反対方向に速度の向きをを少し変更する。

separation: ->

# 回避行動の方向転換計算用cos/sin

cs = Math.cos(Creature._separationAngle)

sn = Math.sin(Creature._separationAngle)

# 自身に最も近い個体

@nearestCreature = null

# 自分以外の群のすべての個体についてサーチ

for other in @cluster.creatures

if other != this

# その個体が自分の前方にいるなら

if other.isInFrontOf(this)

d = Vector.distance(this.pos, other.pos)

# その個体が視野の中にいるなら

if d <= Creature._separationFieldDepth

# 周世に個体がセットされていて、今回の個体の方が近ければ入れ替え

# 最初に認識した個体ならそのままセット

if @nearestCreature?

if d <= Vector.distance(@nearestCreature.pos, this.pos)

@nearestCreature = other

else

@nearestCreature = other

# 近くの個体が視野内に存在するなら回避計算

if @nearestCreature?

# 相手が自分の右にいるなら左へ、自分の左にいるなら右へ向きを変更

if @nearestCreature.isOnTheRightOf(this)

vx = @v.x * cs - @v.y * sn

vy = @v.x * sn + @v.y * cs

else

vx = @v.x * cs + @v.y * sn

vy = -@v.x * sn + @v.y * cs

@v.x = vx

@v.y = vy

# Boids2.2

# 結合行動(cohesion)

# 前方視角180度以内の全個体の重心に向かって速度を少し変更する

cohesion: ->

# 群のうち認識した個体の数とそのグループの重心

n = 0

clusterCenter = null

# 結合行動の方向転換計算用cos/sin

cs = Math.cos(Creature._cohesionAngle)

sn = Math.sin(Creature._cohesionAngle)

# 自分以外の群のすべての個体についてサーチ

for other in @cluster.creatures

if other != this

# 相手が自身の前方にいるなら、その位置を考慮

if other.isInFrontOf(this)

n++

if clusterCenter?

clusterCenter.plusEq(other.pos)

else

clusterCenter = new Vector(other.pos.x, other.pos.y)

# 前方の相手が1つでも存在すれば、結合行動をとる

if clusterCenter?

clusterCenter.divEq(n)

# 重心が自分の右にあれば左に、自分の左にあれば右に進路を変更

if clusterCenter.isOnTheRightOf(this)

vx = @v.x * cs + @v.y * sn

vy = -@v.x * sn + @v.y * cs

else

vx = @v.x * cs - @v.y * sn

vy = @v.x * sn + @v.y * cs

@v.x = vx

@v.y = vy

# Boids2.3

# 整列行動(alignment)

# 分離行動と同じ視野内の個体群の平均速度に合わせるよう速度の方向を変更

alignment: ->

# 平均速度計算用

vMean = null

n = 0

# 整列行動の方向転換計算用cos/sin

cs = Math.cos(Creature._alignmentAngle)

sn = Math.sin(Creature._alignmentAngle)

# 自分以外の群のすべての個体についてサーチ

for other in @cluster.creatures

if other != this

# その個体が自分の前方にいるなら

if other.isInFrontOf(this)

d = Vector.distance(this.pos, other.pos)

# その個体が視野の中にいるなら

if d <= Creature._alignmentFieldDepth

# 既に個体が視野内にあれば平均速度の計算を続行

n++

if vMean?

vMean.plusEq(other.v)

else

vMean = new Vector(0, 0)

# 視野内に個体がいたなら速度変更の計算へ

if vMean?

vMean.divEq(n)

###

@v.plusEq(vMean)

newV = @v.abs()

if newV >= Creature._vMax

@v.timesEq(vMean.abs() / newV)

###

if vMean.isHeadingToRightOf(@v)

vx = @v.x * cs + @v.y * sn

vy = -@v.x * sn + @v.y * cs

else

vx = @v.x * cs - @v.y * sn

vy = @v.x * sn + @v.y * cs

@v.x = vx

@v.y = vy

# Boidsの群を管理するクラスで、以下を保持する

# ・群を構成する複数の個体

# ・個体を描画するcanvasとそのcontextのオブジェクト

class Cluster

# コンストラクタはcanvasオブジェクトを受け取り、そのcontextをプロパティに登録

constructor: (canvas) ->

@creatures = []

@canvas = canvas

@context = @canvas.getContext("2d") if @canvas.getContext

return

# すべての個体オブジェクトを群から削除する

clearCreatures: ->

@creatures = []

# 引数で与えられた個体を群に加える

addCreature: (creature) ->

@creatures.push(creature)

return

# 群の全個体を描画する

# 描画エリアをクリアした後、群の全個体のdraw()メソッドを呼び出している

draw: ->

@context.fillStyle = "#e0e0e0"

@context.fillRect(0, 0, @canvas.width, @canvas.height)

for creature in @creatures

creature.draw(@context)

return

# 秒単位のインターバル受け取り、すべての個体を移動させる

move: (interval_sec) ->

for creature in @creatures

creature.move(interval_sec)

return

# Boidsアプリケーションの動作を統括するクラス

# 唯一、ブラウザから直接呼び出され、初期値の設定やClusterの操作を担当

class Controler

# Boids 1.2からstaticなクラスプロパティとした

@interval_sec: 1 # animation frame interval in seconds

constructor: (canvas) ->

# Boidsの活動領域

@field = new Field(canvas)

# 群のオブジェクト

@cluster = new Cluster(canvas)

# 個体の数

@population = 0

# アニメーション用のフラグとtimer

@isRunning = false

@timer = undefined

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setVMin: (vMin) -> Creature._vMin = vMin

setCreatureSize: (size) -> Creature._drawSize = size

setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix

setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param

setSeparationFieldDepth: (length) -> Creature._separationFieldDepth = length

setSeparationAngle: (angle) -> Creature._separationAngle = angle

setCohesionAngle: (angle) -> Creature._cohesionAngle = angle

setAlignmentFieldDepth: (length) -> Creature._alignmentFieldDepth = length

setAlignmentAngle: (angle) -> Creature._alignmentAngle = angle

setIntervalSec: (@interval_sec) ->

# 一つの個体を発生させるメソッド

# 位置はcanvasに収まるよう、速度はvMax/2～vMaxの範囲でランダム

createCreature: ->

cr = new Creature(@cluster, @field)

x = Math.floor(Math.random() * @field.xMax)

y = Math.floor(Math.random() * @field.yMax)

v = Math.random() * (Creature._vMax - Creature._vMin) + Creature._vMin

a = Math.random() * Math.PI * 2

cr.setPosition(x, y)

cr.setVelocity(v * Math.cos(a), v * Math.sin(a))

return cr

# 引数で指定された数の個体を発生させ、Clusterオブジェクトに登録する

generate: (@population) ->

@cluster.clearCreatures()

for i in [1..@population]

cr = @createCreature()

@cluster.addCreature(cr)

@cluster.draw()

# アニメーションの開始／停止の切り替え

# アニメーションはsetInterval()で実装している

startAndStop: () ->

if @isRunning

clearInterval(@timer)

@isRunning = false

else

@timer = setInterval =>

@cluster.move(@interval_sec)

@cluster.draw()

return

, @interval_sec * 1000

@isRunning = true

return

# 外部からアクセス可能な名前の設定

Boids23.Controler = Controler

# スクリプトが読み込まれた時の実行部分

jQuery ($) ->

# Controlerを作成し、canvasオブジェクトを渡す

canvas = $("#Boids23_canvas")[0]

controler = new Boids23.Controler(canvas)

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD23_V_MAX)

controler.setVMin(BD23_V_MIN)

controler.setCreatureSize(BD23_CREATURE_SIZE)

controler.setWallDetectionLength(BD23_WALL_DETECTION_LENGTH)

controler.setWallRepulsionParam(BD23_WALL_REPULSION_PARAM)

controler.setSeparationFieldDepth(BD23_SEPARATION_FIELD_DEPTH)

controler.setSeparationAngle(BD23_SEPARATION_ANGLE)

controler.setCohesionAngle(BD23_COHESION_ANGLE)

controler.setAlignmentFieldDepth(BD23_ALIGNMENT_FIELD_DEPTH)

controler.setAlignmentAngle(BD23_ALIGNMENT_ANGLE)

controler.setIntervalSec(BD23_INTERVAL_SEC)

# Generateボタンが押されたとき、指定された個体数で群をつくる

$("#boids23_generate").click ->

pop = $("#boids23_population").val()

if pop < 1

pop = 1

$("#boids23_population").val(pop)

controler.generate(pop)

# Start/Stopボタンが押されたとき、アニメーションの動作を切り替える

$("#boids23_start_and_stop").click ->

controler.startAndStop()

↑　Boids 2.2のコード説明へ

↑　Boids 3.0のコード説明へ

Boids 2.2 – コード説明

2016-08-10 / tau / コメントする

概要

Boids 2.2では、分離(Separation)に加えて「結合(Cohesion)」のルールを導入する。結合行動の考え方は、ここでは以下の通りとした。

前方視角内に個体が存在する場合、それらの重心位置を求める
進行方向を、重心の方へ向けて少し変更する

結合のアルゴリズム

重心の算出

次図において、進行方向に直角な直線hより前方側の個体が存在する場合、それらの重心位置gを計算する。

${\bf g} = \frac{1}{n} \sum^n_{i=1} {\bf p}_i$

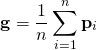
なお、視野角の前方判定はベクトルの前後判定によって行っている。

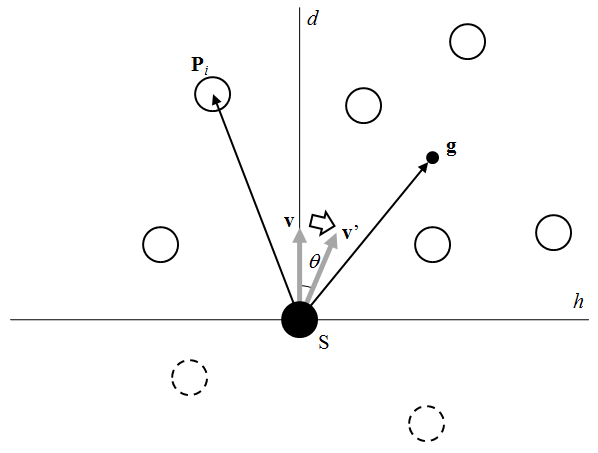
boid2x_cohesion_gravity_center

進路変更

先の図のように、自身の進行方向に対する群の重心の位置によって、以下の手順で進路を変更する。

重心位置が自身の進行方向に対して左右どちら側にあるかを判定
重心位置がが進行方向より右側にあるなら右へ、左側にあるなら左へ方向を少し変化させる。

これらの考え方はBoids 2.1の分離行動における回避動作と同じ。

コード内容

初期パラメータ定義

HTMLで定義する初期パラメータに、結合に関する以下の変数を追加する。

結合の進行方向の変化(BD22_COHESION_ANGLE)

  <script>
  //<![CDATA[
  BD22_V_MAX = 100;
  BD22_CREATURE_SIZE = 10;
  BD22_WALL_DETECTION_LENGTH = 100;
  BD22_WALL_REPULSION_PARAM = 16;
  BD22_VIEW_FIELD_LENGTH = 50;
  BD22_SEPARATION_ANGLE = 10 * Math.PI / 180;
  // Boids 2.2で追加：結合行動の速度の向きを変更する角
  BD22_COHESION_ANGLE = 5 * Math.PI / 180;
  BD22_INTERVAL_SEC = 0.05;
  //]]>
  </script>

//<![CDATA[

BD22_V_MAX = 100;

BD22_CREATURE_SIZE = 10;

BD22_WALL_DETECTION_LENGTH = 100;

BD22_WALL_REPULSION_PARAM = 16;

BD22_VIEW_FIELD_LENGTH = 50;

BD22_SEPARATION_ANGLE = 10 * Math.PI / 180;

// Boids 2.2で追加：結合行動の速度の向きを変更する角

BD22_COHESION_ANGLE = 5 * Math.PI / 180;

BD22_INTERVAL_SEC = 0.05;

//]]>

</script>

クラス変数

初期パラメータの保存のため、Creatureクラスのクラス変数を追加する。

  class Creature extends MovingAgent
    # private ｓtaticなクラス・プロパティ
    # 最大速度
    @_vMax: 100
    # 描画の基本となるサイズ
    @_drawSize: 8
    # 壁の衝突回避を認識する距離
    @_wallDetectionLength:  100
    # 反発力パラメータ
    @_wallRepulsionParam: 4
    # 視野の長さ(奥行)
    @_viewFieldLength: 100
    # 分離行動の回避角
    @_separationAngle: 0
    # 結合行動の回避角
    @_cohesionAngle: 0

class Creature extends MovingAgent

# private ｓtaticなクラス・プロパティ

# 最大速度

@_vMax: 100

# 描画の基本となるサイズ

@_drawSize: 8

# 壁の衝突回避を認識する距離

@_wallDetectionLength: 100

# 反発力パラメータ

@_wallRepulsionParam: 4

# 視野の長さ(奥行)

@_viewFieldLength: 100

# 分離行動の回避角

@_separationAngle: 0

# 結合行動の回避角

@_cohesionAngle: 0

パラメータのセッター

Controlerクラスに、Creatureクラス変数へのセッターを定義する。

  class Controler

    .....

    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setCreatureSize: (size) -> Creature._drawSize = size
    setWallDetectionLength: (pix) -> Creature._wallDetectionLength =  pix
    setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param
    setViewFieldLength: (length) -> Creature._viewFieldLength = length
    setSeparationAngle: (angle) -> Creature._separationAngle = angle
    setCohesionAngle: (angle) -> Creature._cohesionAngle = angle
    setIntervalSec: (@interval_sec) ->

class Controler

.....

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setCreatureSize: (size) -> Creature._drawSize = size

setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix

setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param

setViewFieldLength: (length) -> Creature._viewFieldLength = length

setSeparationAngle: (angle) -> Creature._separationAngle = angle

setCohesionAngle: (angle) -> Creature._cohesionAngle = angle

setIntervalSec: (@interval_sec) ->

パラメータのセット

HTMLで定義されたパラメータをControlerオブジェクトのセッターによってセットする。

# スクリプトが読み込まれた時の実行部分
jQuery ($) ->
  # Controlerを作成し、canvasオブジェクトを渡す
  canvas = $("#Boids22_canvas")[0]
  controler = new Boids22.Controler(canvas)
  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD22_V_MAX)
  controler.setCreatureSize(BD22_CREATURE_SIZE)
  controler.setWallDetectionLength(BD22_WALL_DETECTION_LENGTH)
  controler.setWallRepulsionParam(BD22_WALL_REPULSION_PARAM)
  controler.setViewFieldLength(BD22_VIEW_FIELD_LENGTH)
  controler.setSeparationAngle(BD22_SEPARATION_ANGLE)
  controler.setCohesionAngle(BD22_COHESION_ANGLE)
  controler.setIntervalSec(BD22_INTERVAL_SEC)

  .....

# スクリプトが読み込まれた時の実行部分

jQuery ($) ->

# Controlerを作成し、canvasオブジェクトを渡す

canvas = $("#Boids22_canvas")[0]

controler = new Boids22.Controler(canvas)

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD22_V_MAX)

controler.setCreatureSize(BD22_CREATURE_SIZE)

controler.setWallDetectionLength(BD22_WALL_DETECTION_LENGTH)

controler.setWallRepulsionParam(BD22_WALL_REPULSION_PARAM)

controler.setViewFieldLength(BD22_VIEW_FIELD_LENGTH)

controler.setSeparationAngle(BD22_SEPARATION_ANGLE)

controler.setCohesionAngle(BD22_COHESION_ANGLE)

controler.setIntervalSec(BD22_INTERVAL_SEC)

.....

Ceatureクラスの変更 – cohesion()メソッドの追加

Creatureクラスのmove()メソッドがcohesion()メソッドを呼び出すようにする。

  class Creature extends MovingAgent

    .....

    move: (interval_sec) ->
      # 壁を避ける
      @wallAvoidance()

      # 分離行動(separation)
      @separation()

      # 結合行動(cohesion)
      @cohesion()

      .....

class Creature extends MovingAgent

.....

move: (interval_sec) ->

# 壁を避ける

@wallAvoidance()

# 分離行動(separation)

@separation()

# 結合行動(cohesion)

@cohesion()

.....

coheion()メソッドを新たに定義する。

速度の方向を変化させる回転行列のcos、sinに対応したローカル変数cs、snを定義している
重心位置への参照がclusterCenterプロパティに保存されるが、視野内に個体が存在しないときはnullとなる
速度の回転方向は、右がマイナス方向、左がプラス方向となることに注意

    # Boids2.2
    # 結合行動(cohesion)
    # 前方視角180度以内の全個体の重心に向かって速度を少し変更する
    cohesion: ->
      # 群のうち認識した個体の数とそのグループの重心
      n = 0
      clusterCenter = null
      # 結合行動の方向転換計算用cos/sin
      cs = Math.cos(Creature._cohesionAngle)
      sn = Math.sin(Creature._cohesionAngle)

      # 自分以外の群のすべての個体についてサーチ
      for other in @cluster.creatures
        if other != this
          # 相手が自身の前方にいるなら、その位置を考慮
          if other.isInFrontOf(this)
            n++
            if clusterCenter?
              clusterCenter.plusEq(other.pos)
            else
              clusterCenter = new Vector(other.pos.x, other.pos.y)

      # 前方の相手が1つでも存在すれば、結合行動をとる
      if clusterCenter?
        clusterCenter.divEq(n)
        # 重心が自分の右にあれば左に、自分の左にあれば右に進路を変更
        if clusterCenter.isOnTheRightOf(this)
          vx =  @v.x * cs + @v.y * sn
          vy = -@v.x * sn + @v.y * cs
        else
          vx = @v.x * cs - @v.y * sn
          vy = @v.x * sn + @v.y * cs
        @v.x = vx
        @v.y = vy

# Boids2.2

# 結合行動(cohesion)

# 前方視角180度以内の全個体の重心に向かって速度を少し変更する

cohesion: ->

# 群のうち認識した個体の数とそのグループの重心

n = 0

clusterCenter = null

# 結合行動の方向転換計算用cos/sin

cs = Math.cos(Creature._cohesionAngle)

sn = Math.sin(Creature._cohesionAngle)

# 自分以外の群のすべての個体についてサーチ

for other in @cluster.creatures

if other != this

# 相手が自身の前方にいるなら、その位置を考慮

if other.isInFrontOf(this)

n++

if clusterCenter?

clusterCenter.plusEq(other.pos)

else

clusterCenter = new Vector(other.pos.x, other.pos.y)

# 前方の相手が1つでも存在すれば、結合行動をとる

if clusterCenter?

clusterCenter.divEq(n)

# 重心が自分の右にあれば左に、自分の左にあれば右に進路を変更

if clusterCenter.isOnTheRightOf(this)

vx = @v.x * cs + @v.y * sn

vy = -@v.x * sn + @v.y * cs

else

vx = @v.x * cs - @v.y * sn

vy = @v.x * sn + @v.y * cs

@v.x = vx

@v.y = vy

↑　Boids 2.1のコード説明へ

↓　Boids 2.3のコード説明へ

Boids 2.1 – コード説明

2016-08-10 / tau / コメントする

概要

Boids 2.1では、いよいよBoidsのルールの一つ「分離(Separation)」を導入する。分離行動の考え方は、ここでは以下の通りとした。

視野内に個体が存在するとき、最も距離が近い個体を選択する
その直近個体と反対方向に、自身の進行方向を変化させる

分離のアルゴリズム

視野

個体は自身の進行方向の左右90度以内、180度の視野角を持ち、その視野角内で一定距離以内の個体に反応するものとする。

視野内外の判定の概念は下図の通りで、個体Pは視野内と判定され、個体Qは視野外として無視される。

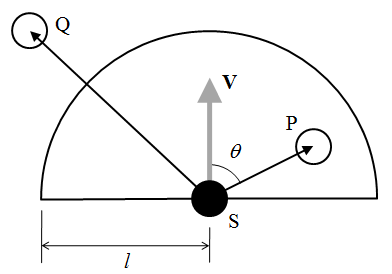
boids2x_perspective

視野内外判定の手順は以下の通り。

前後判定の方法により、視野角内の個体があればそれを選定
その個体について $\overline{\rm SP}} \leqq l$ ならば次へ進む
その個体が最も近いなら入れ替え

回避動作

回避対象が自身の進路の右にいるなら左に、進路の左にいるなら右に、方向ベクトルの角度を変更する。進路変更の角度は予め設定しておく。

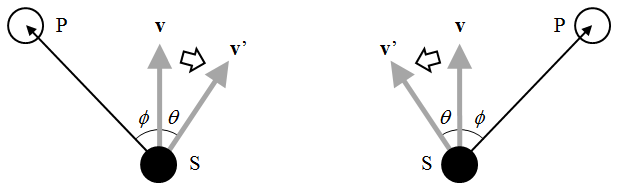
boids2x_separation_avoidance

回避動作の手順は以下の通り。

左右判定の方法により、回避対象が進行方向の左右どちらにあるかを判定
回避対象が進行方向の左にあるなら右へ、右にあるなら左へ方向を少し変化させる。

ここで方向ベクトルの変化量θは予め設定しておき、これに対応するcos、sinによる回転行列を適用して方向を変える。cos、sinの値は、できるだけ計算量が少なくなるようにする。

コード内容

初期パラメータ定義

HTMLで定義する初期パラメータに、分離に関する以下の変数を追加する。

分離に関する視野の深さ(BD21_VIEW_FIELD_LENGTH)
回避行動の進行方向の変化(BD21_SEPARATION_ANGLE)

  <script>
  //<![CDATA[
  BD21_V_MAX = 100;
  BD21_CREATURE_SIZE = 10;
  BD21_WALL_DETECTION_LENGTH = 100;
  BD21_WALL_REPULSION_PARAM = 16;
  // Boids 2.1で追加：視野の深さ
  BD21_VIEW_FIELD_LENGTH = 100;
  // Boids 2.1で追加：分離行動の速度の向きを変更する角
  BD21_SEPARATION_ANGLE = 10 * Math.PI / 180;
  BD21_INTERVAL_SEC = 0.05;
  //]]>
  </script>

//<![CDATA[

BD21_V_MAX = 100;

BD21_CREATURE_SIZE = 10;

BD21_WALL_DETECTION_LENGTH = 100;

BD21_WALL_REPULSION_PARAM = 16;

// Boids 2.1で追加：視野の深さ

BD21_VIEW_FIELD_LENGTH = 100;

// Boids 2.1で追加：分離行動の速度の向きを変更する角

BD21_SEPARATION_ANGLE = 10 * Math.PI / 180;

BD21_INTERVAL_SEC = 0.05;

//]]>

</script>

クラス変数

初期パラメータの保存のため、Creatureクラスのクラス変数を追加する。

  class Creature extends taustation_geom2d.MovingAgent
    # private ｓtaticなクラス・プロパティ
    # 最大速度
    @_vMax: 100
    # 描画の基本となるサイズ
    @_drawSize: 8
    # 壁の衝突回避を認識する距離
    @_wallDetectionLength:  100
    # 反発力パラメータ
    @_wallRepulsionParam: 4
    # 視野の長さ(奥行)
    @_viewFieldLength: 100
    # 分離行動の回避計算用
    @_separationAngle: 0

class Creature extends taustation_geom2d.MovingAgent

# private ｓtaticなクラス・プロパティ

# 最大速度

@_vMax: 100

# 描画の基本となるサイズ

@_drawSize: 8

# 壁の衝突回避を認識する距離

@_wallDetectionLength: 100

# 反発力パラメータ

@_wallRepulsionParam: 4

# 視野の長さ(奥行)

@_viewFieldLength: 100

# 分離行動の回避計算用

@_separationAngle: 0

パラメータのセッター

Controlerクラスに、Creatureクラス変数へのセッターを定義する。

  class Controler

    .....

    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setCreatureSize: (size) -> Creature._drawSize = size
    setWallDetectionLength: (pix) -> Creature._wallDetectionLength =  pix
    setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param
    setViewFieldLength: (length) -> Creature._viewFieldLength = length
    setSeparationAngle: (angle) -> Creature._separationAngle = angle
    setIntervalSec: (@interval_sec) ->

class Controler

.....

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setCreatureSize: (size) -> Creature._drawSize = size

setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix

setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param

setViewFieldLength: (length) -> Creature._viewFieldLength = length

setSeparationAngle: (angle) -> Creature._separationAngle = angle

setIntervalSec: (@interval_sec) ->

パラメータのセット

HTMLで定義されたパラメータをControlerオブジェクトのセッターによってセットする。

jQuery ($) ->
  # Controlerを作成し、canvasオブジェクトを渡す
  canvas = $("#Boids21_canvas")[0]
  controler = new Boids21.Controler(canvas)
  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD21_V_MAX)
  controler.setCreatureSize(BD21_CREATURE_SIZE)
  controler.setWallDetectionLength(BD21_WALL_DETECTION_LENGTH)
  controler.setWallRepulsionParam(BD21_WALL_REPULSION_PARAM)
  controler.setViewFieldLength(BD21_VIEW_FIELD_LENGTH)
  controler.setSeparationAngle(BD21_SEPARATION_ANGLE)
  controler.setIntervalSec(BD21_INTERVAL_SEC)

  # Generateボタンが押されたとき、指定された個体数で群をつくる
  $("#boids21_generate").click ->
    pop = $("#boids21_population").val()
    if pop < 1
      pop = 1
      $("#boids21_population").val(pop)
    controler.generate(pop)

  # Start/Stopボタンが押されたとき、アニメーションの動作を切り替える
  $("#boids21_start_and_stop").click ->
    controler.startAndStop()

jQuery ($) ->

# Controlerを作成し、canvasオブジェクトを渡す

canvas = $("#Boids21_canvas")[0]

controler = new Boids21.Controler(canvas)

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD21_V_MAX)

controler.setCreatureSize(BD21_CREATURE_SIZE)

controler.setWallDetectionLength(BD21_WALL_DETECTION_LENGTH)

controler.setWallRepulsionParam(BD21_WALL_REPULSION_PARAM)

controler.setViewFieldLength(BD21_VIEW_FIELD_LENGTH)

controler.setSeparationAngle(BD21_SEPARATION_ANGLE)

controler.setIntervalSec(BD21_INTERVAL_SEC)

# Generateボタンが押されたとき、指定された個体数で群をつくる

$("#boids21_generate").click ->

pop = $("#boids21_population").val()

if pop < 1

pop = 1

$("#boids21_population").val(pop)

controler.generate(pop)

# Start/Stopボタンが押されたとき、アニメーションの動作を切り替える

$("#boids21_start_and_stop").click ->

controler.startAndStop()

Ceatureクラスの変更 – separation()メソッドの追加

Creatureクラスのmove()メソッドがseparation()メソッドを呼び出すようにする。

  class Creature extends MovingAgent

    .....

    move: (interval_sec) ->
      # 壁を避ける
      @wallAvoidance()

      # 分離行動(separation)
      @separation()

      .....

class Creature extends MovingAgent

.....

move: (interval_sec) ->

# 壁を避ける

@wallAvoidance()

# 分離行動(separation)

@separation()

.....

separation()メソッドを新たに定義する。

速度の方向を変化させる回転行列のcos、sinに対応したローカル変数cs、snを定義している
最も近い個体への参照がnearestCreatureプロパティに保存されるが、視野内に個体が存在しないときはnullとなる
速度の回転方向は、右がマイナス方向、左がプラス方向となることに注意

    # Boids2.1
    # 分離行動(separation)
    # 前方視角180度内で一定距離内の視野の中で、最も近い個体を避ける
    # 相手方の速度の向きには関係なく、相手側と反対方向に速度の向きをを少し変更する。
    separation: ->
      # 回避行動の方向転換計算用cos/sin
      cs = Math.cos(Creature._separationAngle)
      sn = Math.sin(Creature._separationAngle)
      # 自身に最も近い個体
      @nearestCreature = null

      # 自分以外の群のすべての個体についてサーチ
      for other in @cluster.creatures
        if other != this
          # その個体が自分の前方にいるなら
          if other.isInFrontOf(this)
            d = Vector.distance(this.pos, other.pos)
            # その個体が視野の中にいるなら
            if d <= Creature._viewFieldLength
              # 既に個体がセットされていて、今回の個体の方が近ければ入れ替え
              # 最初に認識した個体ならそのままセット
              if @nearestCreature?
                if d <= Vector.distance(@nearestCreature.pos, this.pos)
                  @nearestCreature = other
              else
                @nearestCreature = other
      # 近くの個体が視野内に存在するなら回避計算
      if @nearestCreature?
        # 相手が自分の右にいるなら左へ、自分の左にいるなら右へ向きを変更
        if @nearestCreature.isOnTheRightOf(this)
          vx = @v.x * cs - @v.y * sn
          vy = @v.x * sn + @v.y * cs
        else
          vx =  @v.x * cs + @v.y * sn
          vy = -@v.x * sn + @v.y * cs
        @v.x = vx
        @v.y = vy

# Boids2.1

# 分離行動(separation)

# 前方視角180度内で一定距離内の視野の中で、最も近い個体を避ける

# 相手方の速度の向きには関係なく、相手側と反対方向に速度の向きをを少し変更する。

separation: ->

# 回避行動の方向転換計算用cos/sin

cs = Math.cos(Creature._separationAngle)

sn = Math.sin(Creature._separationAngle)

# 自身に最も近い個体

@nearestCreature = null

# 自分以外の群のすべての個体についてサーチ

for other in @cluster.creatures

if other != this

# その個体が自分の前方にいるなら

if other.isInFrontOf(this)

d = Vector.distance(this.pos, other.pos)

# その個体が視野の中にいるなら

if d <= Creature._viewFieldLength

# 既に個体がセットされていて、今回の個体の方が近ければ入れ替え

# 最初に認識した個体ならそのままセット

if @nearestCreature?

if d <= Vector.distance(@nearestCreature.pos, this.pos)

@nearestCreature = other

else

@nearestCreature = other

# 近くの個体が視野内に存在するなら回避計算

if @nearestCreature?

# 相手が自分の右にいるなら左へ、自分の左にいるなら右へ向きを変更

if @nearestCreature.isOnTheRightOf(this)

vx = @v.x * cs - @v.y * sn

vy = @v.x * sn + @v.y * cs

else

vx = @v.x * cs + @v.y * sn

vy = -@v.x * sn + @v.y * cs

@v.x = vx

@v.y = vy

↑　Boids 2.0のコード説明へ

↓　Boids 2.2のコード説明へ

Boids 2.0 – コード説明

2016-08-10 / tau / コメントする

概要

Boids 2.0は以後のBoids 2.xシリーズの土台となるもので、Boids 1.2に対して以下を変更している。

位置と速度を持ったCreatureクラスのうち、位置と速度の保持、互いの位置関係の判定に関する性質を汎用のMovingAgentクラスとしてまとめ、taustation-geo2dパッケージに含めた
初期パラメータをHTMLのスクリプトに置き、再コンパイルしなくてもパラメータを変更しやすくなるようにした。

MovingAgentクラスの導入

CreatureクラスはMovingAgentクラスを継承し、それらのメソッドを利用する。

  class Creature extends MovingAgent

1	class Creature extends MovingAgent

MovingAgentのプロパティを継承するため、位置と速度の指定が変更。たとえばCreatureクラスのインスタンスがcreatureだとすると、以下のようになる。

位置のx座標は、creature:pos.x
位置のy座標は、creature:pos.y
速度のx成分は、creature:v.x
速度のy成分は、creature:v.y

HTMLでの初期パラメータ設定

概要

各種パラメータの設定を、CoffeeScriptの再コンパイルやアップロードをしなくても、HTMLで設定・変更できるようにした。

必要なパラメータをHTMLのスクリプトで定義
以下のパラメータをセットするセッターを、全てControlerクラスのメソッドとして集約
- 個体に関するパラメータはCreatureのクラス変数
- アニメーションのインターバルはControlerクラスのプロパティ
スクリプト読み込み時に、Controlerオブジェクトのセッターにグローバル・パラメータ変数を渡してパラメータ設定

初期パラメータ定義

HTMLにパラメータをグローバル変数としてスクリプト記述。

注意点は、スクリプトはJavascriptにコンパイルされているので、直接読み込まれるグローバル変数もJavascriptの変数として書くこと。特に各定義の文末にセミコロン(;)を付けること。

  <script>
  //<![CDATA[
  BD20_V_MAX = 100;
  BD20_CREATURE_SIZE = 10;
  BD20_WALL_DETECTION_LENGTH = 100;
  BD20_WALL_REPULSION_PARAM = 16;
  BD20_INTERVAL_SEC = 0.05;
  //]]>
  </script>

//<![CDATA[

BD20_V_MAX = 100;

BD20_CREATURE_SIZE = 10;

BD20_WALL_DETECTION_LENGTH = 100;

BD20_WALL_REPULSION_PARAM = 16;

BD20_INTERVAL_SEC = 0.05;

//]]>

</script>

クラス変数

上記のパラメータのうち、個体の運動に関わるものを、Creatureクラスのクラス変数として定義。

なお、アニメーションのフレーム・インターバル(interval_sec)は、Controlerクラスのクラス変数として定義している。

  class Creature extends taustation_geom2d.MovingAgent
    # private ｓtaticなクラス・プロパティ
    # 最大速度
    @_vMax: 100
    # 描画の基本となるサイズ
    @_drawSize: 8
    # 壁の衝突回避を認識する距離
    @_wallDetectionLength:  100
    # 反発力パラメータ
    @_wallRepulsionParam: 4

class Creature extends taustation_geom2d.MovingAgent

# private ｓtaticなクラス・プロパティ

# 最大速度

@_vMax: 100

# 描画の基本となるサイズ

@_drawSize: 8

# 壁の衝突回避を認識する距離

@_wallDetectionLength: 100

# 反発力パラメータ

@_wallRepulsionParam: 4

パラメータのセッター

上記のクラス変数にパラメータをセットするセッターを、Controlerクラスのメソッドとして集約。

  class Controler

    .....

    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setCreatureSize: (size) -> Creature._drawSize = size
    setWallDetectionLength: (pix) -> Creature._wallDetectionLength =  pix
    setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param
    setIntervalSec: (@interval_sec) ->

class Controler

.....

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setCreatureSize: (size) -> Creature._drawSize = size

setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix

setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param

setIntervalSec: (@interval_sec) ->

パラメーターのセット

スクリプト実行時に、上記セッターを通してグローバル変数のパラメータを設定する。

jQuery ($) ->

  .....

  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD20_V_MAX)
  controler.setCreatureSize(BD20_CREATURE_SIZE)
  controler.setWallDetectionLength(BD20_WALL_DETECTION_LENGTH)
  controler.setWallRepulsionParam(BD20_WALL_REPULSION_PARAM)
  controler.setIntervalSec(BD20_INTERVAL_SEC)

jQuery ($) ->

.....

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD20_V_MAX)

controler.setCreatureSize(BD20_CREATURE_SIZE)

controler.setWallDetectionLength(BD20_WALL_DETECTION_LENGTH)

controler.setWallRepulsionParam(BD20_WALL_REPULSION_PARAM)

controler.setIntervalSec(BD20_INTERVAL_SEC)

Boids 2.0の全コード

# Boids 2.1
# Boids 2.0 = 1.2に基づいて、分離(separation)ルールを導入する。
Boids20 = {}

# パッケージBoids20の本体
do ->
  # 独自クラスのエイリアス
  # パッケージtaustation_geom2d.jsが必要。
  Vector = taustation_geom2d.Vector
  MovingAgent = taustation_geom2d.MovingAgent

  # Boidsが活動する空間のクラス
  # このバージョンでは、canvasオブジェクトの上下左右の座標を持つ長方形
  class Field
    constructor: (canvas) ->
      @xMin = 0
      @yMin = 0
      @xMax = canvas.width
      @yMax = canvas.height


  # Boidsの個体を実現するクラス
  # 位置座標と速度ベクトルの成分を保持する
  # 自らが活動するFieldクラスのオブジェクトへの参照も保持する
  class Creature extends taustation_geom2d.MovingAgent
    # private ｓtaticなクラス・プロパティ
    # 最大速度
    @_vMax: 100
    # 描画の基本となるサイズ
    @_drawSize: 8
    # 壁の衝突回避を認識する距離
    @_wallDetectionLength:  100
    # 反発力パラメータ
    @_wallRepulsionParam: 4

    # コンストラクタの引数にはFieldオブジェクトを渡す
    # 位置、速度、加速度、自分が属する群、Fieldをプロパティとして持つ
    constructor: (cluster, field) ->
      super()
      @a = new Vector(0, 0)
      @cluster = cluster
      @field = field
      @nearestCreature = null

    # 個体を描画するメソッド
    # canvasのコンテキストを引数で受け取る
    draw: (ctx) ->
      v = @v.abs()
      sx = Creature._drawSize * @v.x / v
      sy = Creature._drawSize * @v.y / v
      p = 0.25

      ctx.fillStyle = "black"
      ctx.beginPath()
      ctx.moveTo(@pos.x + (1 - p) * sx, @pos.y + (1 - p) * sy)
      ctx.lineTo(@pos.x + (-sx - sy) * p, @pos.y + (sx - sy) * p)
      ctx.lineTo(@pos.x + (-sx + sy) * p, @pos.y + (-sx - sy) * p)
      ctx.closePath()
      ctx.fill()
      return

    # 個体を動かすメソッド
    # 「群れ」を表すClusterクラスのmove()メソッドから呼ばれる
    # interval_secは秒単位のアニメーション・フレームのインターバル
    move: (interval_sec) ->
      # 壁を避ける
      @wallAvoidance()

      # 加速度を考慮した速度の変化を計算
      # 速度の絶対値が増え続けないようにキャップで抑える
      # 速度成分の符号を得るのに、Math.signがサポートされていないブラウザが多いため、
      # 値/絶対値で符号を得ている
      @v.plusEq(@a.times interval_sec)
      @v.x = @v.x / Math.abs(@v.x) * Math.min(Math.abs(@v.x), Creature._vMax)
      @v.y = @v.y / Math.abs(@v.y) * Math.min(Math.abs(@v.y), Creature._vMax)

      # インターバルの間の移動量を計算
      @pos.plusEq(@v.times interval_sec)

      # 壁にぶつかった場合は全反射
      if @pos.x <= @field.xMin or @pos.x >= @field.xMax then @v.x = -@v.x
      if @pos.y <= @field.yMin or @pos.y >= @field.yMax then @v.y = -@v.y

      return

    # 壁を避ける行動
    # 壁からの距離に応じた斥力を(repulsion)想定し、ｘ/ｙ方向の加速度を計算
    wallAvoidance: ->
      if @pos.x <= Creature._wallDetectionLength
        @a.x =
          Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / @pos.x) ** 2
      else if @pos.x >= @field.xMax - Creature._wallDetectionLength
        @a.x =
          -Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / (@field.xMax - @pos.x)) ** 2
      else
        @a.x = 0

      if @pos.y <= Creature._wallDetectionLength
        @a.y =
          Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / @pos.y) ** 2
      else if @pos.y >= @field.yMax - Creature._wallDetectionLength
        @a.y =
          -Creature._wallRepulsionParam *
          (Creature._wallDetectionLength / (@field.yMax - @pos.y)) ** 2
      else
        @a.y = 0


  # Boidsの群を管理するクラスで、以下を保持する
  # ・群を構成する複数の個体
  # ・個体を描画するcanvasとそのcontextのオブジェクト
  class Cluster
    # コンストラクタはcanvasオブジェクトを受け取り、そのcontextをプロパティに登録
    constructor: (canvas) ->
      @creatures = []
      @canvas = canvas
      @context = @canvas.getContext("2d") if @canvas.getContext
      return

    # すべての個体オブジェクトを群から削除する
    clearCreatures: ->
      @creatures = []

    # 引数で与えられた個体を群に加える
    addCreature: (creature) ->
      @creatures.push(creature)
      return

    # 群の全個体を描画する
    # 描画エリアをクリアした後、群の全個体のdraw()メソッドを呼び出している
    draw: ->
      @context.fillStyle = "#e0e0e0"
      @context.fillRect(0, 0, @canvas.width, @canvas.height)
      for creature in @creatures
        creature.draw(@context)
      return

    # 秒単位のインターバル受け取り、すべての個体を移動させる
    move: (interval_sec) ->
      for creature in @creatures
        creature.move(interval_sec)
      return


  # Boidsアプリケーションの動作を統括するクラス
  # 唯一、ブラウザから直接呼び出され、初期値の設定やClusterの操作を担当
  class Controler
    # Boids 1.2からstaticなクラスプロパティとした
    @interval_sec: 1 # animation frame interval in seconds

    constructor: (canvas) ->
      # Boidsの活動領域
      @field = new Field(canvas)
      # 群のオブジェクト
      @cluster = new Cluster(canvas)
      # 個体の数
      @population = 0
      # アニメーション用のフラグとtimer
      @isRunning = false
      @timer = undefined

    # 定数として扱うクラス変数を設定するメソッド群
    setVMax: (vMax) -> Creature._vMax = vMax
    setCreatureSize: (size) -> Creature._drawSize = size
    setWallDetectionLength: (pix) -> Creature._wallDetectionLength =  pix
    setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param
    setIntervalSec: (@interval_sec) ->

    # 一つの個体を発生させるメソッド
    # 位置はcanvasに収まるよう、速度はvMax/2～vMaxの範囲でランダム
    createCreature: ->
      cr = new Creature(@cluster, @field)
      x = Math.floor(Math.random() * @field.xMax)
      y = Math.floor(Math.random() * @field.yMax)
      v = (Math.random() + 1) * Creature._vMax / 2
      a = Math.random() * Math.PI * 2
      cr.setPosition(x, y)
      cr.setVelocity(v * Math.cos(a), v * Math.sin(a))
      return cr

    # 引数で指定された数の個体を発生させ、Clusterオブジェクトに登録する
    generate: (@population) ->
      @cluster.clearCreatures()
      for i in [1..@population]
        cr = @createCreature()
        @cluster.addCreature(cr)
      @cluster.draw()

    # アニメーションの開始／停止の切り替え
    # アニメーションはsetInterval()で実装している
    startAndStop: () ->
      if @isRunning
        clearInterval(@timer)
        @isRunning = false
      else
        @timer = setInterval =>
          @cluster.move(@interval_sec)
          @cluster.draw()
          return
        , @interval_sec * 1000
        @isRunning = true
      return

  # 外部からアクセス可能な名前の設定
  Boids20.Controler = Controler


# スクリプトが読み込まれた時の実行部分
jQuery ($) ->
  # Controlerを作成し、canvasオブジェクトを渡す
  canvas = $("#Boids20_canvas")[0]
  controler = new Boids20.Controler(canvas)
  # 固定パラメータのセット
  # パラメータの値は、Javascript形式でHTMLに埋め込まれている想定
  controler.setVMax(BD20_V_MAX)
  controler.setCreatureSize(BD20_CREATURE_SIZE)
  controler.setWallDetectionLength(BD20_WALL_DETECTION_LENGTH)
  controler.setWallRepulsionParam(BD20_WALL_REPULSION_PARAM)
  controler.setIntervalSec(BD20_INTERVAL_SEC)

  # Generateボタンが押されたとき、指定された個体数で群をつくる
  $("#boids20_generate").click ->
    pop = $("#boids20_population").val()
    if pop < 1
      pop = 1
      $("#boids20_population").val(pop)
    controler.generate(pop)

  # Start/Stopボタンが押されたとき、アニメーションの動作を切り替える
  $("#boids20_start_and_stop").click ->
    controler.startAndStop()

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

# Boids 2.1

# Boids 2.0 = 1.2に基づいて、分離(separation)ルールを導入する。

Boids20 = {}

# パッケージBoids20の本体

do ->

# 独自クラスのエイリアス

# パッケージtaustation_geom2d.jsが必要。

Vector = taustation_geom2d.Vector

MovingAgent = taustation_geom2d.MovingAgent

# Boidsが活動する空間のクラス

# このバージョンでは、canvasオブジェクトの上下左右の座標を持つ長方形

class Field

constructor: (canvas) ->

@xMin = 0

@yMin = 0

@xMax = canvas.width

@yMax = canvas.height

# Boidsの個体を実現するクラス

# 位置座標と速度ベクトルの成分を保持する

# 自らが活動するFieldクラスのオブジェクトへの参照も保持する

class Creature extends taustation_geom2d.MovingAgent

# private ｓtaticなクラス・プロパティ

# 最大速度

@_vMax: 100

# 描画の基本となるサイズ

@_drawSize: 8

# 壁の衝突回避を認識する距離

@_wallDetectionLength: 100

# 反発力パラメータ

@_wallRepulsionParam: 4

# コンストラクタの引数にはFieldオブジェクトを渡す

# 位置、速度、加速度、自分が属する群、Fieldをプロパティとして持つ

constructor: (cluster, field) ->

super()

@a = new Vector(0, 0)

@cluster = cluster

@field = field

@nearestCreature = null

# 個体を描画するメソッド

# canvasのコンテキストを引数で受け取る

draw: (ctx) ->

v = @v.abs()

sx = Creature._drawSize * @v.x / v

sy = Creature._drawSize * @v.y / v

p = 0.25

ctx.fillStyle = "black"

ctx.beginPath()

ctx.moveTo(@pos.x + (1 - p) * sx, @pos.y + (1 - p) * sy)

ctx.lineTo(@pos.x + (-sx - sy) * p, @pos.y + (sx - sy) * p)

ctx.lineTo(@pos.x + (-sx + sy) * p, @pos.y + (-sx - sy) * p)

ctx.closePath()

ctx.fill()

return

# 個体を動かすメソッド

# 「群れ」を表すClusterクラスのmove()メソッドから呼ばれる

# interval_secは秒単位のアニメーション・フレームのインターバル

move: (interval_sec) ->

# 壁を避ける

@wallAvoidance()

# 加速度を考慮した速度の変化を計算

# 速度の絶対値が増え続けないようにキャップで抑える

# 速度成分の符号を得るのに、Math.signがサポートされていないブラウザが多いため、

# 値/絶対値で符号を得ている

@v.plusEq(@a.times interval_sec)

@v.x = @v.x / Math.abs(@v.x) * Math.min(Math.abs(@v.x), Creature._vMax)

@v.y = @v.y / Math.abs(@v.y) * Math.min(Math.abs(@v.y), Creature._vMax)

# インターバルの間の移動量を計算

@pos.plusEq(@v.times interval_sec)

# 壁にぶつかった場合は全反射

if @pos.x <= @field.xMin or @pos.x >= @field.xMax then @v.x = -@v.x

if @pos.y <= @field.yMin or @pos.y >= @field.yMax then @v.y = -@v.y

return

# 壁を避ける行動

# 壁からの距離に応じた斥力を(repulsion)想定し、ｘ/ｙ方向の加速度を計算

wallAvoidance: ->

if @pos.x <= Creature._wallDetectionLength

@a.x =

Creature._wallRepulsionParam *

(Creature._wallDetectionLength / @pos.x) ** 2

else if @pos.x >= @field.xMax - Creature._wallDetectionLength

@a.x =

-Creature._wallRepulsionParam *

(Creature._wallDetectionLength / (@field.xMax - @pos.x)) ** 2

else

@a.x = 0

if @pos.y <= Creature._wallDetectionLength

@a.y =

Creature._wallRepulsionParam *

(Creature._wallDetectionLength / @pos.y) ** 2

else if @pos.y >= @field.yMax - Creature._wallDetectionLength

@a.y =

-Creature._wallRepulsionParam *

(Creature._wallDetectionLength / (@field.yMax - @pos.y)) ** 2

else

@a.y = 0

# Boidsの群を管理するクラスで、以下を保持する

# ・群を構成する複数の個体

# ・個体を描画するcanvasとそのcontextのオブジェクト

class Cluster

# コンストラクタはcanvasオブジェクトを受け取り、そのcontextをプロパティに登録

constructor: (canvas) ->

@creatures = []

@canvas = canvas

@context = @canvas.getContext("2d") if @canvas.getContext

return

# すべての個体オブジェクトを群から削除する

clearCreatures: ->

@creatures = []

# 引数で与えられた個体を群に加える

addCreature: (creature) ->

@creatures.push(creature)

return

# 群の全個体を描画する

# 描画エリアをクリアした後、群の全個体のdraw()メソッドを呼び出している

draw: ->

@context.fillStyle = "#e0e0e0"

@context.fillRect(0, 0, @canvas.width, @canvas.height)

for creature in @creatures

creature.draw(@context)

return

# 秒単位のインターバル受け取り、すべての個体を移動させる

move: (interval_sec) ->

for creature in @creatures

creature.move(interval_sec)

return

# Boidsアプリケーションの動作を統括するクラス

# 唯一、ブラウザから直接呼び出され、初期値の設定やClusterの操作を担当

class Controler

# Boids 1.2からstaticなクラスプロパティとした

@interval_sec: 1 # animation frame interval in seconds

constructor: (canvas) ->

# Boidsの活動領域

@field = new Field(canvas)

# 群のオブジェクト

@cluster = new Cluster(canvas)

# 個体の数

@population = 0

# アニメーション用のフラグとtimer

@isRunning = false

@timer = undefined

# 定数として扱うクラス変数を設定するメソッド群

setVMax: (vMax) -> Creature._vMax = vMax

setCreatureSize: (size) -> Creature._drawSize = size

setWallDetectionLength: (pix) -> Creature._wallDetectionLength = pix

setWallRepulsionParam: (param) -> Creature._wallRepulsionParam = param

setIntervalSec: (@interval_sec) ->

# 一つの個体を発生させるメソッド

# 位置はcanvasに収まるよう、速度はvMax/2～vMaxの範囲でランダム

createCreature: ->

cr = new Creature(@cluster, @field)

x = Math.floor(Math.random() * @field.xMax)

y = Math.floor(Math.random() * @field.yMax)

v = (Math.random() + 1) * Creature._vMax / 2

a = Math.random() * Math.PI * 2

cr.setPosition(x, y)

cr.setVelocity(v * Math.cos(a), v * Math.sin(a))

return cr

# 引数で指定された数の個体を発生させ、Clusterオブジェクトに登録する

generate: (@population) ->

@cluster.clearCreatures()

for i in [1..@population]

cr = @createCreature()

@cluster.addCreature(cr)

@cluster.draw()

# アニメーションの開始／停止の切り替え

# アニメーションはsetInterval()で実装している

startAndStop: () ->

if @isRunning

clearInterval(@timer)

@isRunning = false

else

@timer = setInterval =>

@cluster.move(@interval_sec)

@cluster.draw()

return

, @interval_sec * 1000

@isRunning = true

return

# 外部からアクセス可能な名前の設定

Boids20.Controler = Controler

# スクリプトが読み込まれた時の実行部分

jQuery ($) ->

# Controlerを作成し、canvasオブジェクトを渡す

canvas = $("#Boids20_canvas")[0]

controler = new Boids20.Controler(canvas)

# 固定パラメータのセット

# パラメータの値は、Javascript形式でHTMLに埋め込まれている想定

controler.setVMax(BD20_V_MAX)

controler.setCreatureSize(BD20_CREATURE_SIZE)

controler.setWallDetectionLength(BD20_WALL_DETECTION_LENGTH)

controler.setWallRepulsionParam(BD20_WALL_REPULSION_PARAM)

controler.setIntervalSec(BD20_INTERVAL_SEC)

# Generateボタンが押されたとき、指定された個体数で群をつくる

$("#boids20_generate").click ->

pop = $("#boids20_population").val()

if pop < 1

pop = 1

$("#boids20_population").val(pop)

controler.generate(pop)

# Start/Stopボタンが押されたとき、アニメーションの動作を切り替える

$("#boids20_start_and_stop").click ->

controler.startAndStop()

↓　Boids 2.1のコード説明へ

CoffeeScript – Boids 2.x – ルールの実装

2016-08-10 / tau / コメントする

Boids 2.xの概要

Boids 2.xシリーズでは、Boids 1.xで準備した土台となるコードに、個体の行動ルール(分離、結合、整列)を一つずつ実装していく。

Boids 2.0　Boids1.2のコードを以下のように変更。
- Creatureクラスから汎用のMovingAgentクラスを分離して、これを継承
- 初期パラメータの設定値をHTMLに置いて、変更しやすくした
Boids 2.1　分離(Separation)のルールを適用し、互いの衝突を避けるようにする。
Boids 2.2　結合(Cohesion)のルールを適用し、個体が群に集まろうとする傾向を持たせる。
Boids 2.3　整列(Alignment)のルールを適用し、個体が皆と同じ方向に動こうとする傾向を持たせる。

Boids 2.0 – 基本コード

基本コードの挙動はBoids 1.2と同じで、各個体は壁との衝突を避けながら自由に動くが、他の個体は意識しない。

Boids 2.0のコード詳細

Boids 2.1 – 分離(Separation)

個体同士の衝突を避けるように進路を変更する行動ルールを適用する。他の個体が接近したときに、それぞれが進路を変更している様子がわかる。

Boids 2.1のコード詳細

Boids 2.2 – 結合(Cohesion)

各個体が、視野内の群の重心に向かって進路を変更するルールを適用する。全体として群を形成しようとする様子がわかる。

Boids 2.2のコード詳細

Boids 2.3 – 整列(Alignment)

各個体が、視野内の群の全体としての移動方向に自分の進路を合わせるよう変更するルールを適用する。群が全体として同じ方向に動こうとしている様子がわかる。

Boids 2.3のコード詳細

↑　Boids 1.x

CoffeeScript – geom2d.MovingAgentクラス

2016-08-07 / tau / コメントする

パッケージ

taustation_geom2d

クラス名

taustation_geom2d.MovingAgent

クラス仕様

概要

自分の位置を表すVectorオブジェクトと移動速度を表すVectorオブジェクトを要素に持ち、他のMovingAgentとの位置関係を判定するメソッドを準備している。

なお、Vectorクラスには、Vectorを位置ベクトルとしたときに、その点とMovingAgentとの位置関係を表すメソッドが用意されている。

クラス変数

なし

クラス・メソッド

なし

インスタンス・プロパティ

pos: 自らの位置を保持するVectorオブジェクト
v: 自らの移動速度を保持するVectorオブジェクト

コンストラクタ

constructor(): 位置(0, 0)、速度(0, 0)のMovingAgentインスタンスを生成する。

インスタンス・メソッド

基本メソッド

setPosition(x, y): MovingAgentの位置をx、yの座標値で指定する。
setVelocity(vx, vy): MovingAgentの速度をvx、vyの成分で指定する。
getClone(): 元のMovingAgentオブジェクトと同じ内容のクローンを生成して返す。

判定

isInFrontOf(other): このMovingAgentオブジェクトが引数のMovingAgentオブジェクトの前方(左右180度より進行方向の側)にあるときtrue、後方にあるときfalseを返す。真横の時は前方と判定される。
isIntheRearOf(other): isInFrontOf()と前後逆の判定結果を返す。
isOnTheRightOf(other): このMovingAgentオブジェクトが引数のMovingAgentオブジェクトの右方にあるときtrue、左方にあるときfalseを返す。進行方向の延長線上にあるときは右方と判定される。
isOnTheLeftOf(movingAgent): isOnTheRightOf()と左右逆の判定結果を返す。

コード

  class MovingAgent
    constructor: ->
      @pos = new Vector(0, 0)
      @v = new Vector(0, 0)
      return

    # 個体の位置をセットするメソッド
    setPosition: (x, y) ->
      @pos.x = x
      @pos.y = y
      return

    # 個体の速度をセットするメソッド
    setVelocity: (vx, vy) ->
      @v.x = vx
      @v.y = vy
      return
      
    # 自身と同じ内容のMovingAgentオブジェクトを生成して返す
    getClone: ->
      clone = new MovingAgent()
      clone.setPosition(@pos.x, @pos.y)
      clone.setVelocity(@v.x, @v.y)
      return clone

    # 以下、他のMovingAgentとの位置関係
    #
    # このMovingAgentが引数のMovingAgentの前方か
    isInFrontOf: (other) ->
      inprod = other.v.x * (@pos.x - other.pos.x) +
               other.v.y * (@pos.y - other.pos.y)
      if inprod >= 0 then true else false

    # このMovingAgentが引数のMovingAgentの後方か
    isInTheRearOf: (other) -> not @isInFrontOf(other)

    # このMovingAgentが引数のMovingAgentの右方か
    isOnTheRightOf: (other) ->
      inprod = other.v.y * (@pos.x - other.pos.x) -
               other.v.x * (@pos.y - other.pos.y)
      if inprod >= 0 then true else false

    # このMovingAgentが引数のMovingAgentの左方か
    isOnTheLeftOf: (other) -> not @isOnTheRightOf(other)

class MovingAgent

constructor: ->

@pos = new Vector(0, 0)

@v = new Vector(0, 0)

return

# 個体の位置をセットするメソッド

setPosition: (x, y) ->

@pos.x = x

@pos.y = y

return

# 個体の速度をセットするメソッド

setVelocity: (vx, vy) ->

@v.x = vx

@v.y = vy

return

# 自身と同じ内容のMovingAgentオブジェクトを生成して返す

getClone: ->

clone = new MovingAgent()

clone.setPosition(@pos.x, @pos.y)

clone.setVelocity(@v.x, @v.y)

return clone

# 以下、他のMovingAgentとの位置関係

# このMovingAgentが引数のMovingAgentの前方か

isInFrontOf: (other) ->

inprod = other.v.x * (@pos.x - other.pos.x) +

other.v.y * (@pos.y - other.pos.y)

if inprod >= 0 then true else false

# このMovingAgentが引数のMovingAgentの後方か

isInTheRearOf: (other) -> not @isInFrontOf(other)

# このMovingAgentが引数のMovingAgentの右方か

isOnTheRightOf: (other) ->

inprod = other.v.y * (@pos.x - other.pos.x) -

other.v.x * (@pos.y - other.pos.y)

if inprod >= 0 then true else false

# このMovingAgentが引数のMovingAgentの左方か

isOnTheLeftOf: (other) -> not @isOnTheRightOf(other)

直線のパラメータ表示と操作

2016-08-03 / tau / コメントする

直線のパラメータ表示

たとえば2次元の直線のパラメータ表示は、以下のように一つのパラメータtに対してxとyが計算される方法。

$\left\{ \begin{align*} x = a t + b \\ y = c t + d \end{align} \right.$

直線の決定

通過点と方向が与えられた場合

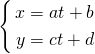
直線が通過すべき点(p_x, p_y)と、直線の方向(v_x, v_y)が与えられた場合のパラメータ表示を決定する。

通過点でパラメータがt = 0とすればp_xとp_yが定まり、tが1単位増えた時のxとyの増分が直線の方向に対応することから、以下のように表される。

$\left\{ \begin{align*} x = v_x t + p_x \\ y = v_y t + p_y \end{align} \right.$

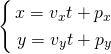
なおこれらを、パラメータtに対応した直線状の点の位置ベクトル ${\bf x}$ 、通過点の位置ベクトル ${\bf p}$ 、方向ベクトル ${\bf v}$ で表示すると下記のようになる。

${\bf x} = {\bf v} t + {\bf p}$

2つの通過点が与えられた場合

2つの点p(p_x, p_y)とq(q_x, q_y)が与えられた場合の直線のパラメータ表示を決定する。

点pでt = 0、点qでt = 1とすれば、以下の式が得られる。

$\left\{ \begin{align*} x = (q_x - p_x) t + p_x \\ y = (q_y - p_y) t + p_y \end{align} \right.$

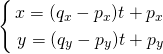
これをベクトル表示すれば以下の通り。

${\bf x} = ( {\bf q} - {\bf p} ) t + {\bf p}$

直線の式との関係

一般に直線の式は以下で与えられる。

$ax + by + c = 0$

一方で媒介変数された直線の式からパラメーターを消去すると以下のようになる。

$\frac{x - p_x}{v_x} = \frac{y - p_y}{v_y}$

これを変形すると、先の直線の式との対応関係がわかる。

$v_y x - v_x y -v_x p_x + v_y p_y = 0$

交点の特定

以下の2つの直線の交点を求める。

$\left\{ \begin{align*} {\bf x}_1 = {\bf v}_1 t_1 + {\bf p}_1 \\ {\bf x}_2 = {\bf v}_2 t_2 + {\bf p}_2 \end{align}$

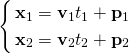
これを要素表示に展開する。

$\left\{ \begin{align*} x_1 = v_{1x} t_1 + p_{1x} \\ y_1 = v_{1y} t_1 + p_{1y} \\ x_2 = v_{2x} t_2 + p_{2x} \\ y_2 = v_{2y} t_2 + p_{2y} \end{align}$

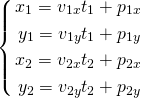
ここでx₁ = x₂、y₁ = y₂と置いて、t₁、t₂を未知数とした以下の方程式を得る。

$\left\{ \begin{align*} v_{1x} t_1 + p_{1x} = v_{2x} t_2 + p_{2x} \\ v_{1y} t_1 + p_{1y} = v_{2y} t_2 + p_{2y} \end{align}$

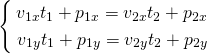
この方程式を行列で表示すると以下の通り。

$\left[ \begin{array}{cc} v_{1x} & -v_{2x} \\ v_{1y} & -v_{2y} \end{array} \right] \left[ \begin{array}{c} t_1 \\ t_2 \end{array} \right] = \left[ \begin{array}{c} p_{2x} - p_{1x} \\ p_{2y} - p_{1y} \end{array} \right] = \left[ \begin{array}{c} \Delta p_x \\ \Delta p_y \end{array} \right]$

これを解いて以下を得る。

$\left\{ \begin{align*} t_1 = \frac{-v_{2y} \Delta p_x + v_{2x} \Delta p_y}{-v_{1x}v_{2y} + v_{1y} v_{2x}} \\ t_2 = \frac{-v_{1y} \Delta p_x + v_{1x} \Delta p_y}{-v_{1x}v_{2y} + v_{1y} v_{2x}} \end{align} \right.$

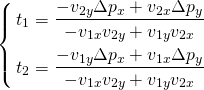
これらの式は分母がゼロのときは解をもたないが、これは ${\bf v}_1$ と ${\bf v}_2$ を90度回転させたベクトルが直角であること、すなわち2つの直線の方向が平行であることを示している。

さらに2つの直線がまったく一致するときは、分母・分子ともゼロとなり、解は不定となる。

ここで、交点の座標を確認する。

$\begin{align*} x &= v_{1x} t_1 + p_{1x} = v_{2x} t_2 + p_{2x} \\ &= \frac{v_{1y} v_{2x} p_{1x} - v_{1x} v_{2y} p_{2x} + v_{1x} v_{2x}(p_{2y} - p_{1y})} {-v_{1x} v_{2y} + v_{1y} v_{2x}} \\ y &= v_{1y} t_1 + p_{1y} = v_{2y} t_2 + p_{2y} \\ &= \frac{v_{1y} v_{2y} (p_{2x} - p_{1x}) - v_{1x} v_{2y} p_{1y} + v_{1y} v_{2x} p_{2y}} {-v_{1x} v_{2y} + v_{1y} v_{2x}} \end{align}$

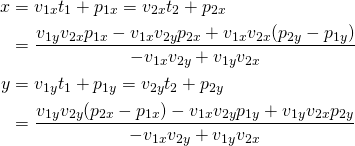
当然この結果は、パラメータ表示の2直線からパラメータt₁、t₂を消去して陰関数表示をした以下の方程式の解と一致する。

$\left\{ \begin{align*} v_{1y} x - v_{1x} y = v_{1y} p_{1x} - v_{1x} p_{1y} \\ v_{2y} x - v_{2x} y = v_{2y} p_{2x} - v_{2x} p_{2y} \end{align} \right.$

交点の位置

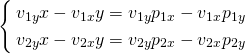
パラメータ表示の場合、基準点においてt = 0とし、方向ベクトルの先、あるいはそれに相当する2つ目の点においてt = 1などとすれば、基準点から方向ベクトルの先のtは正の値、逆方向ではtが負の値になる。

これを利用して、二つの直線の交点が基準点より前方／後方どちらの側にあるか、あるいは半直線に交点が存在するか、といった判定が容易に可能となる。

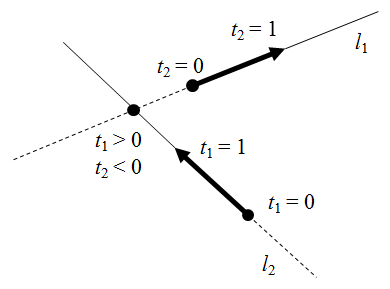
math_geom_line1

ベクトルの内積

2016-08-03 / tau / コメントする

ベクトルの内積の表現には、要素表示を用いたものと幾何的なものの2つがある。

${\bf a} \cdot {\bf b} = a_x b_x + a_y b_y + a_z b_z = | {\bf a} | | {\bf b} | \cos \theta$

2つの表現が等価であることを証明するのに、下図のように2つのベクトルで張られた三角形の $\oberline{AB}$ の長さを考える。

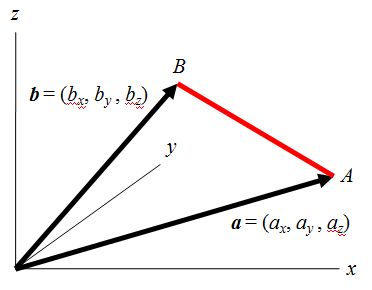
math_vector_innerprod_1

まずベクトルの成分で計算した場合は、

$\begin{align*} \overline{AB}^2 &= (a_x - b_x)^2 + (a_y - b_y)^2 + (a_z - b_z)^2 \\ &= a_x^2 + a_y^2 + a_z^2 + b_x^2 + b_y^2 + b_z^2 - 2 a_x b_x - 2 a_y b_y - 2 a_z b_z \end{align}$

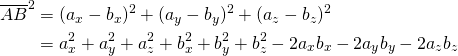
また余弦定理を用いて計算した場合は、 $a = | {\bf a} | , \: b = | {\bf b} |$ として以下のようになる。

$\begin{align*} \overline{AB}^2 &= a^2 + b^2 - 2ab \cos \theta \\ &= a_x^2 + a_y^2 + a_z^2 + b_x^2 + b_y^2 + b_z^2 - 2ab \cos \theta \end{align}$

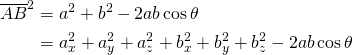
上記2つが等しいことから、以下が得られる。

$a_x b_x + a_y b_y + a_z b_z = ab \cos \theta$

2次元の場合は、z成分を0とおいてx成分とy成分のみについて考えればよい。