コイン
コイントスで表→1、裏→0としたときの平均、分散。分布は{表, 裏]の一様分布。
平均
(1) ![]()
分散
(2) ![]()
サイコロ
サイコロ1つを投げたときの目の数の平均、分散。分布は{1,2, 3, 4, 5, 6}の一様分布。
平均
(3) 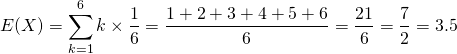
分散
(4) 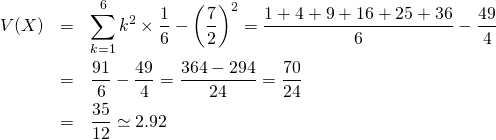
トランプ
トランプを一枚引いたときの数の平均、分散。ここでAは1とする。分布は{1, …, 13}の一様分布。
平均
(5) 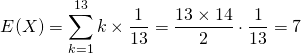
分散
(6) 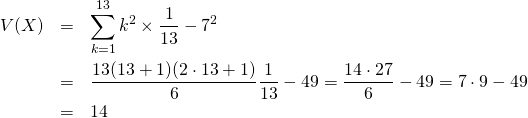
コイントスで表→1、裏→0としたときの平均、分散。分布は{表, 裏]の一様分布。
(1) ![]()
(2) ![]()
サイコロ1つを投げたときの目の数の平均、分散。分布は{1,2, 3, 4, 5, 6}の一様分布。
(3) 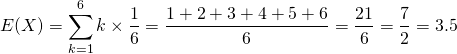
(4) 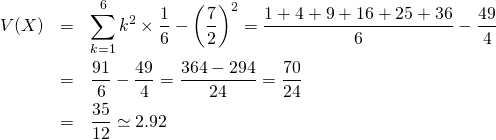
トランプを一枚引いたときの数の平均、分散。ここでAは1とする。分布は{1, …, 13}の一様分布。
(5) 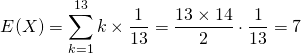
(6) 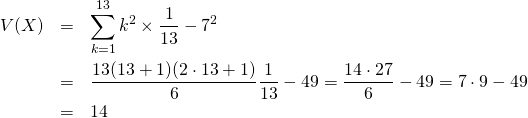
大数の法則を簡単に言うと、「標本の数を多くとるほど、標本平均の値は母平均に近づく」というもので、感覚的には当たり前と思われることだが、数学的に証明できる。
「それでは、どの位の数を取ったときに、どの程度の平均からのズレで収まるのか?」という問に対しては、大数の法則は答えていない。
大数の法則には弱法則と強法則の2つがあり、それぞれ次のように表される。
標本平均![]() の標本数を限りなく多くとれば、その
の標本数を限りなく多くとれば、その![]() が平均
が平均![]() の近傍からはずれる確率をいくらでも小さくできる。
の近傍からはずれる確率をいくらでも小さくできる。
(1) ![]()
チェビシェフの不等式に![]() を適用する。
を適用する。
(2) ![]()
ここで標本平均の期待値と分散を適用して極限をとると
(3) ![]()
標本平均![]() の標本数を限りなく多くとれば、
の標本数を限りなく多くとれば、![]() はほぼ確実に(確率1で)
はほぼ確実に(確率1で)![]() に収束する。
に収束する。
(4) ![]()
対数の強法則は弱法則に比べて強い主張であり、その分証明は難しくなるとのこと。
平均![]() 、分散
、分散![]() の正規分布
の正規分布![]() の確率密度関数は以下の通り。
の確率密度関数は以下の通り。
(1) ![]()
この場合、![]() となる確率は以下のように表される。
となる確率は以下のように表される。
(2) ![]()
ここで、確率変数を以下のように変換する。
(3) ![]()
これを式(2)に適用し、![]() に留意して、
に留意して、
(4) ![]()
標準正規分布の確率に対する確率変数![]() の値を覚えていれば、母集団の平均と標準偏差が与えられたとき、上記の変数変換を行って、確率値を得ることができる。
の値を覚えていれば、母集団の平均と標準偏差が与えられたとき、上記の変数変換を行って、確率値を得ることができる。
厚生労働省による「平成29年国民健康・栄養調査報告」によると、26歳~29歳の日本人男性の身長は、平均が171.0cm、標準偏差が5.8cmとなっている。この年代層で身長が180cmを超える確率は、
(5) ![]()
このuの典型的な値と確率のセットを覚えておけば、確率を知ることができる。この場合は1.5より少し大きいので、超過確率は6%程度とわかる(より正確には6.04%)。
![]() が0.5なら3割程度、1なら16%、1.5で6.7%になる。
が0.5なら3割程度、1なら16%、1.5で6.7%になる。
逆に超過確率25%なら![]() =0.67、10%なら1.28、5%(両側90%以内)で1.64、2.5%(両側95%以内)なら1.96。
=0.67、10%なら1.28、5%(両側90%以内)で1.64、2.5%(両側95%以内)なら1.96。
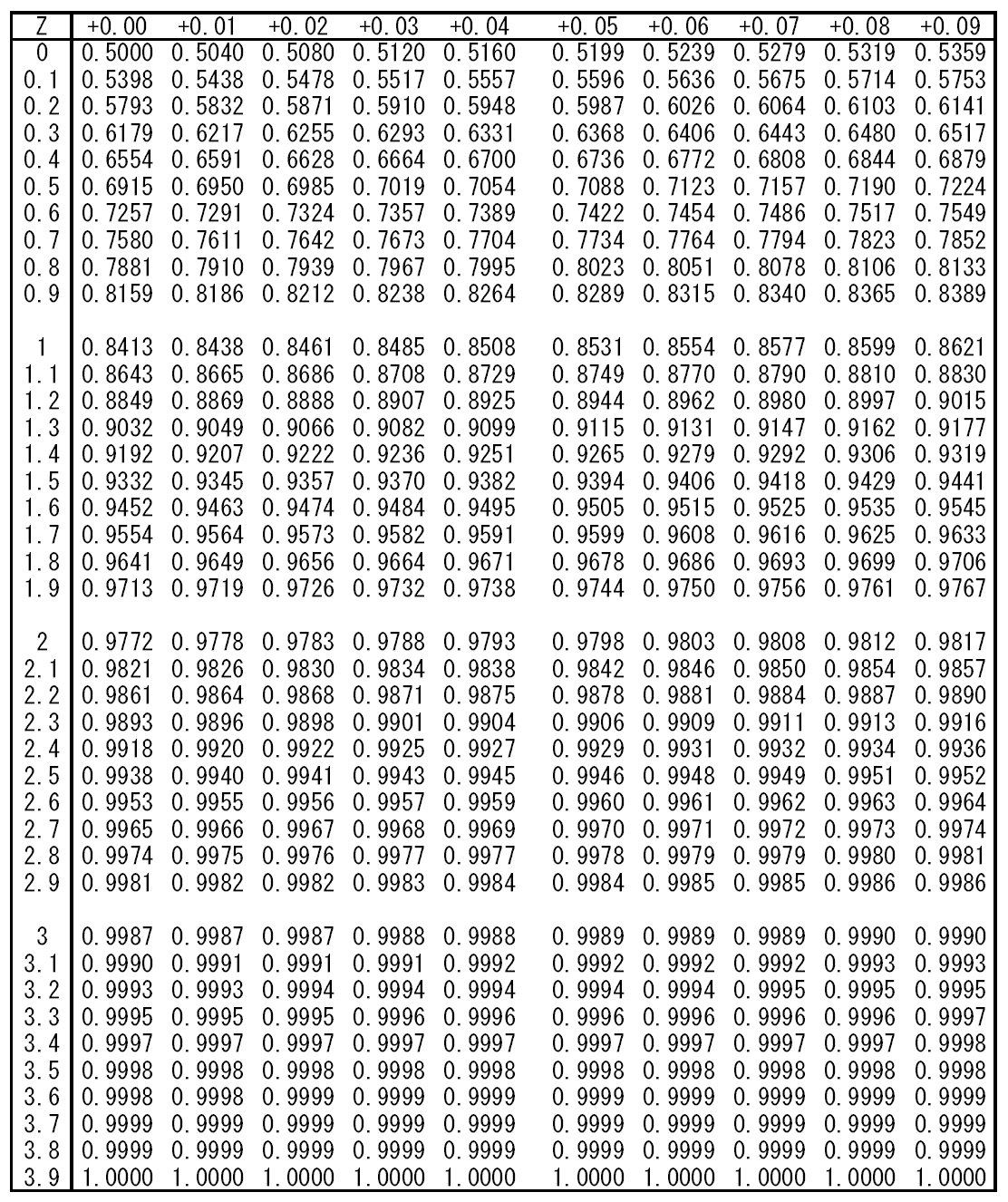
標準正規分布の![]() に対する確率
に対する確率![]() の
の![]() に対する確率は標準正規分布表で与えられているが、以下の値は覚えておくとよい。
に対する確率は標準正規分布表で与えられているが、以下の値は覚えておくとよい。
| z | ||
| 0.5 | 0.31 | 0.38 |
| 0.67449 (0.67) | 0.25 | 0.5 |
| 0.84162 | 0.2 | 0.6 |
| 1 | 0.16 | 0.68 |
| 1.03643 | 0.15 | 0.7 |
| 1.15035 | 0.125 | 0.75 |
| 1.28155 (1.28) | 0.1 | 0.8 |
| 1.5 | 0.067 | 0.87 |
| 1.64485 (1.64) | 0.05 | 0.9 |
| 1.95996 (1.96) | 0.025 | 0.95 |
| 2 | 0.023 | 0.95 |
| 2.32635 (2.32) | 0.01 | 0.98 |
| 2.57584 (2.58) | 0.005 | 0.99 |
チェビシェフの不等式は何がありがたいかというと、「確率分布がどのようなものであっても、平均と分散の値さえわかっていれば、確率変数の値が平均からはずれる確率がいくら以下か計算できる」ということにある。
たとえばあるデータの平均が![]() 、分散が
、分散が![]() とわかっているとき、データが
とわかっているとき、データが![]() から
から![]() より外れる確率が少なくともどの程度以下か(あるいはその範囲に収まる確率が少なくともどの程度以上か)、というのを教えてくれる。
より外れる確率が少なくともどの程度以下か(あるいはその範囲に収まる確率が少なくともどの程度以上か)、というのを教えてくれる。
チェビシェフの不等式は、以下のようにいくつかの表し方がある
(1) ![]()
ここで![]() とおけば、
とおけば、
(2) ![]()
これを余事象で表すと、
(3) ![]()
ただし、これらの式において![]() 。
。
この不等式の意義は、確率変数がどのような確率分布に従っているとしても成り立つところにある。ただし、その過程で相当の”切り落とし”をしているので実用的な精度ではない。
たとえば母集団が標準正規分布に従う場合、![]() に対して0.9545、0.9973であるのに対して、チェビシェフの不等式では
に対して0.9545、0.9973であるのに対して、チェビシェフの不等式では![]() となる確率は
となる確率は![]() に対して、
に対して、![]() 以上となる。
以上となる。
離散確率で、![]() の値に応じて確率変数を以下のように区分する。
の値に応じて確率変数を以下のように区分する。
(4) ![]()
また、以下の確率分布を定義する。
(5) ![]()
このとき、以下が成り立つ。
(6) 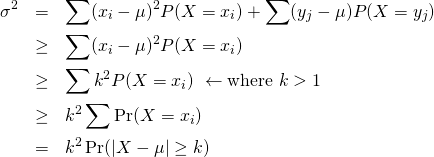
(7) ![]()
確率の定義から以下が成り立つ。
(8) ![]()
ここで、以下のように変数を変換する。
(9) ![]()
これより、以下が成り立つ。
(10) 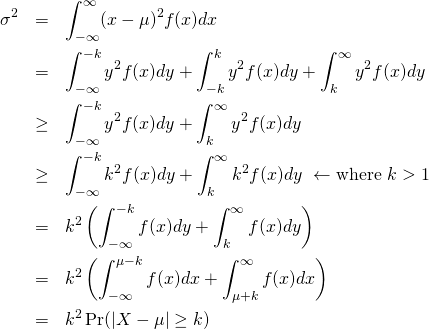
(11) ![]()
スクリプトを作業ディレクトリに保存しておくと、コンソールからの実行がしやすい。
作業ディレクトリの確認方法は
|
1 |
> getwd() |
[CTRL]+R、エディタのカーソル行以降の文が1行ずつ実行される。[CTRL]+Aで全選択して[CTRL]+Rとすると、すべての文が実行される。
スクリプトが作業ディレクトリにある場合は、以下のコマンドで直接実行。
|
1 |
> source('foo.R') |
標本分散![]() は次式で求められる。この
は次式で求められる。この![]() と、母分散
と、母分散![]() の関係を導いてゆく。
の関係を導いてゆく。
(1) 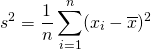
以後、![]() のパラメータを省略する。まず
のパラメータを省略する。まず![]() を母平均として、
を母平均として、![]() を以下のように変形する。
を以下のように変形する。
(2) 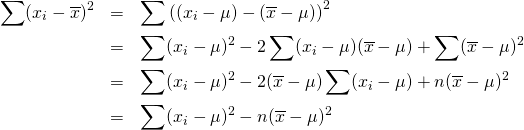
これより、標本分散![]() の期待値は以下のようになる。
の期待値は以下のようになる。
(3) 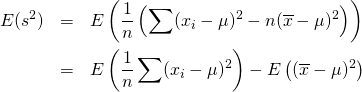
1項目については、
(4) ![]()
また第2項目は標本平均の分散より、
(5) ![]()
これらより、標本分散の期待値は以下のようになる。
(6) ![]()
式(6)より、母分散を得るために以下のように変形。
(7) ![]()
これは、左辺の()の中が母分散![]() の不偏推定量であることを示している。このことから、母分散に対する不偏分散
の不偏推定量であることを示している。このことから、母分散に対する不偏分散![]() は次式で表される。
は次式で表される。
(8) ![]()
不偏分散の分母が![]() となっているのは、母分散なら
となっているのは、母分散なら![]() となるところが、標本の計算では
となるところが、標本の計算では![]() であり、
であり、![]() が他の標本から計算されることから、変数の数(自由度)が1少ないことを表している。自由度が少なければ、目指す値を計算するデータが一つ少なくなり、ばらつきはその分大きくなる。
が他の標本から計算されることから、変数の数(自由度)が1少ないことを表している。自由度が少なければ、目指す値を計算するデータが一つ少なくなり、ばらつきはその分大きくなる。
標本平均の期待値、分散について考える。イメージとして、母集団からn個の標本値を取り出して期待値![]() を計算し、これを繰り返した場合の
を計算し、これを繰り返した場合の![]() の平均と分散を求めることになる。
の平均と分散を求めることになる。
まず、![]() の期待値については以下のように計算され、標本平均の期待値が母平均の不偏推定量であることがわかる。
の期待値については以下のように計算され、標本平均の期待値が母平均の不偏推定量であることがわかる。
(1) 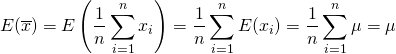
次に![]() の分散は以下のように計算される。
の分散は以下のように計算される。
(2) 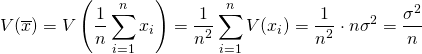
ここで、xiはそれぞれ独立に選ばれることから、V(x1, …, xn)は線形に分解できる。
標本平均![]() の分散がXの母分散をnで割った値となっているのは、標本平均を計算する項数が多いほど期待値に対する誤差が小さくなることを示唆している。
の分散がXの母分散をnで割った値となっているのは、標本平均を計算する項数が多いほど期待値に対する誤差が小さくなることを示唆している。
式(2)は、次のように偏差の自乗和の期待値でも表現できる。
(3) ![]()
標本X1, …, Xnの母集団が正規分布N(μ, σ2)に従うとき、標本の和X1 + ··· + Xnは正規分布N(nμ, nσ2)に従い標本平均![]() はN(μ, σ2/n)に従うことが知られている。
はN(μ, σ2/n)に従うことが知られている。
また母集団の分布が正規分布でないとしても、中心極限定理により、標本の数(この場合は平均を取り出す回数)を多くすれば、その平均は正規分布に従う。
標本分散・母分散は、標本値や確率変数の平均からの偏差の自乗平均で定義される。
(1) 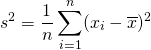
(2) 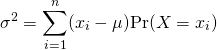
(3) ![]()
分散の定義の一般形は以下の通りで、母集団の確率分布によらない。
(4) ![]()
(5) 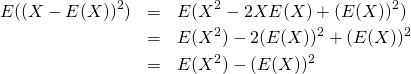
分散には以下の性質がある。
(6) ![]()
(7) ![]()
(8) ![]()
標本値、確率変数に定数を加えても、分散の値は変わらない。これは、分散が各標本値・確率変数の平均からの偏差の平均であり、定数のバイアスはキャンセルアウトされることから明らかでもある。
![]()
(9) 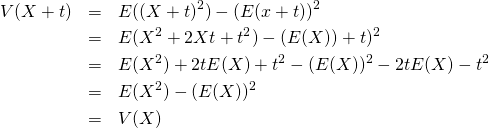
標本値、確率変数を定数倍した場合、分散の値は定数の自乗倍になる。これは、分散の定義の形からも明らか。
![]()
(10) 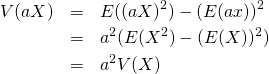
二つの標本値の組や確率変数を加えた場合の分散は、それぞれの分散の和に双方の共分散を加えた値になる。平均のような線形性がなく、2変数の和の2乗を展開した形と類似している。
![]()
(11) 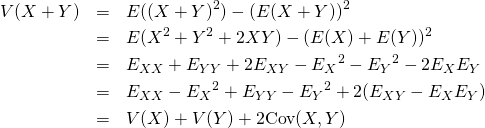
上式で![]() などと置き換えている。
などと置き換えている。
3つ確率変数の和の場合は以下の通りで、3つの変数の和の2乗を展開した形と類似している。
(12) ![]()
(13) 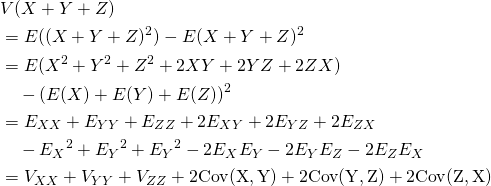
確率変数![]() と
と![]() が独立なとき、次項で示すように共分散がゼロとなり、以下が成り立つ。
が独立なとき、次項で示すように共分散がゼロとなり、以下が成り立つ。
(14) ![]()
2つの標本値、確率変数の共分散は以下で定義される。
(15) 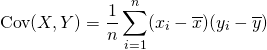
これは以下のようにも表現できる。
(16) ![]()
(17) 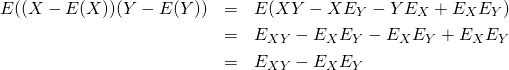
共分散は、2つの標本値、確率変数に正の相関が強い場合に生となり、負の相関が強い場合に負となる。また、相関が弱い場合にゼロに近くなる。
共分散の変数に定数を加えても、加える前の共分散と同じ値になる。定数をいずれの変数に加えても同じ。
(18) 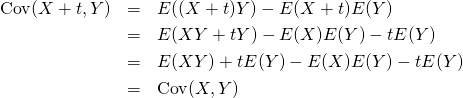
共分散の変数を定数倍すると、もとの共分散の定数倍になる。両方の変数を定数倍すると、もとの共分散に双方の定数の積を乗じた値になる。
(19) 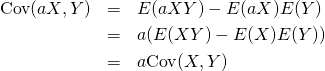
標本値、確率変数の和は、加える前の個々の共分散の和になる。すなわち、共分散においては分配法則が成り立つ。
(20) ![]()
(21) 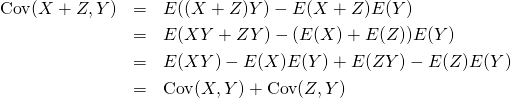
2つの確率変数の事象が独立な場合、共分散はゼロとなる。
![]() と
と![]() が独立ならば、その同時生起確率はそれぞれの確率の積となるので。
が独立ならば、その同時生起確率はそれぞれの確率の積となるので。
(22) ![]()
これより
(23) 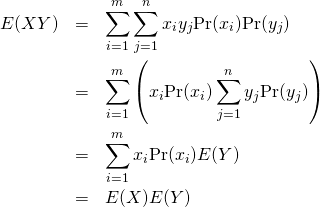
これを定義式に適用して![]() が確認できる。
が確認できる。
![]() と
と![]() が独立なとき、その確率密度はそれぞれの確率密度の積となる。
が独立なとき、その確率密度はそれぞれの確率密度の積となる。
(24) ![]()
これより
(25) 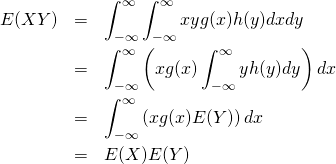
これを定義式に適用して![]() が確認できる。
が確認できる。
XとYが完全な線形関係にある場合の共分散は、XまたはY(いずれでもよい)の分散の定数倍になる。
(26) 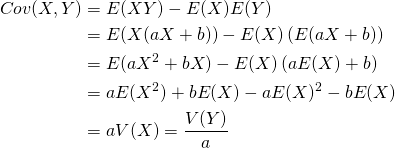
平均の定義には標本平均と確率変数の平均があって、それぞれ定義が異なるので、ここで整理する。
標本平均に対しては算術平均、幾何平均、調和平均などの定義があるが、ここでは算術平均を対象とする。
標本平均は、標本データの値を足し合わせてその個数で割った値。
標本の値が![]() のとき、標本平均
のとき、標本平均![]() は標本値の算術平均で定義される。
は標本値の算術平均で定義される。
(1) 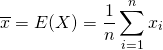
確率変数の平均は、離散型の場合と連続型の場合それぞれで定義される。
離散型の確率変数![]() が
が![]() の値を取り、それぞれの値をとる確率を
の値を取り、それぞれの値をとる確率を![]() と表すと、
と表すと、![]() の母平均
の母平均![]() は確率変数とその確率変数の発生確率の積の総和で定義される。
は確率変数とその確率変数の発生確率の積の総和で定義される。
(2) 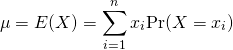
連続型の確率変数の平均は、確率密度関数を![]() とすると、
とすると、![]() の母平均
の母平均![]() は、確率変数とその値に対する確率密度の積の全定義域における積分で定義される。
は、確率変数とその値に対する確率密度の積の全定義域における積分で定義される。
(3) ![]()
平均(期待値)には以下の性質がある。これらは、母集団の確率分布に関係なく常に成り立つ。
(4) ![]()
(5) ![]()
(6) ![]()
標本値、確率変数に定数を加えた場合の平均は、元の平均に定数を加えた値に等しい。
![]()
(7) 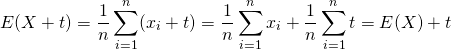
(8) 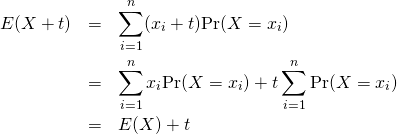
(9) 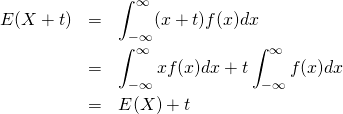
標本値、確率変数を定数倍した場合の平均は、元の平均の定数倍に等しい。
![]()
(10) 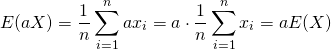
(11) 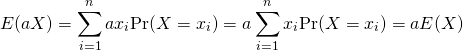
(12) ![]()
複数の標本値(データセット)、確率変数を加えた場合の平均は、それぞれの平均の和に等しい
![]()
(13) 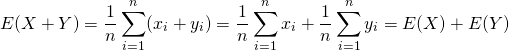
確率変数![]() が
が![]() 、
、![]() が
が![]() であり、
であり、![]() 、
、![]() はそれぞれの確率分布に従うとする。また、
はそれぞれの確率分布に従うとする。また、![]() と
と![]() の同時生起確率を
の同時生起確率を![]() と表す。
と表す。
このとき、確率変数![]() の平均は以下のように計算される。
の平均は以下のように計算される。
(14) 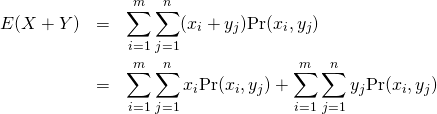
上式の第1項についてみると、![]() の値に対してすべての
の値に対してすべての![]() のとりうる値を考慮していることから、
のとりうる値を考慮していることから、![]() とそれに対する生起確率
とそれに対する生起確率![]() となり、第1項は
となり、第1項は![]() の平均となる。
の平均となる。
(15) 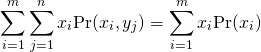
第2項も同様に![]() の平均なので、以下が成り立つ。
の平均なので、以下が成り立つ。
![]()
確率変数![]() に対する同時生起確率密度を
に対する同時生起確率密度を![]() とすると、
とすると、
(16) 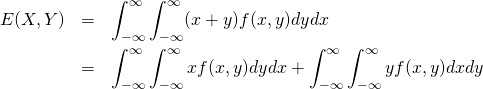
離散型と同様の考え方により、上式の第1項、第2項はそれぞれ![]() の平均となり、次式が成り立つ。
の平均となり、次式が成り立つ。
![]()
QuickLaTeXでディスプレイ数式を書くとき、通常のequationやeqnarrayを使うと自動的に番号が付けられるが、番号をつけない方法とまとめて整理した。
equationブロックにする。
|
1 2 3 4 5 |
[latex] \begin{equation} y = a x + b \end{equation} [/latex] |
(1) ![]()
equation*を使う。
|
1 2 3 4 5 |
[latex] \begin{equation*} y = a x + b \end{equation*} [/latex] |
![]()
eqnarrayブロックにする。
QuickLaTeXの場合、式番号は連立方程式群に一つの番号がつく。個別の式に番号をつけるためのnumcases、subnumcasesは機能しない。
等号を揃えるには、等号の前後を&で挟む。
|
1 2 3 4 5 6 |
[latex] \begin{eqnarray} a &=& y + z \\ u + v &=& w \end{eqnarray} [/latex] |
(2) ![]()
eqnarray*を使う。
|
1 2 3 4 5 6 |
[latex] \begin{eqnarray*} x &=& y + z \\ u + v &=& w \end{eqnarray*} [/latex] |
![]()