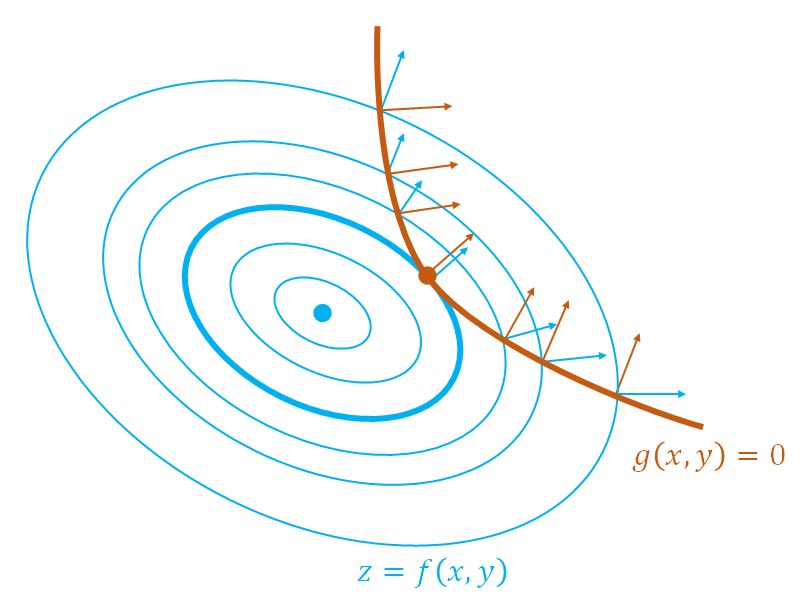
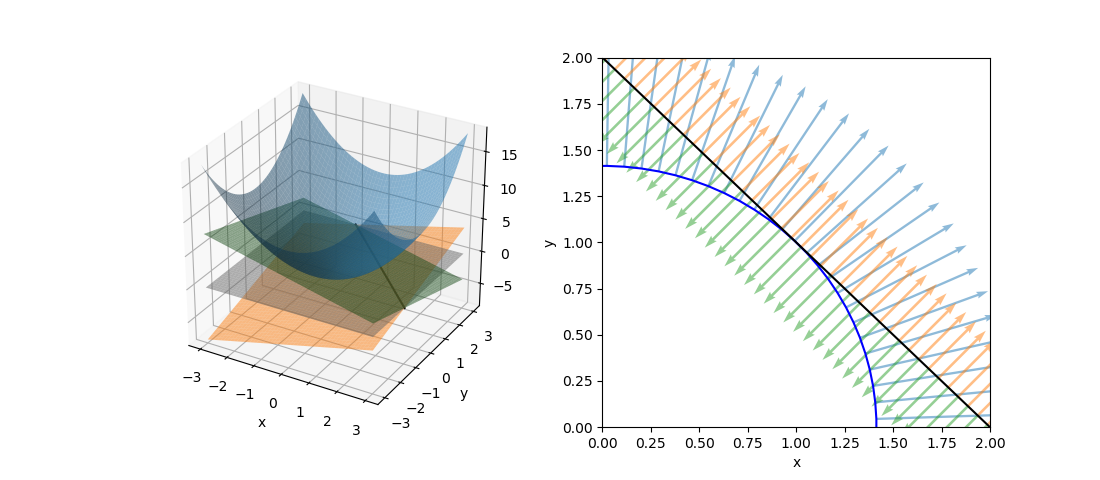
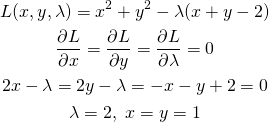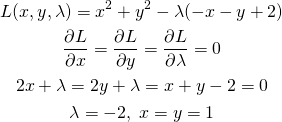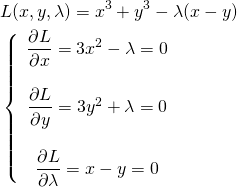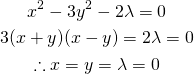Irisデータセット

2020-03-08 / tau / コメントする

概要

Irisデータセットはアヤメの種類と特徴量に関するデータセットで、3種類のアヤメの花弁と萼(がく)に関する特徴量について多数のデータを提供する。

ここではPythonのscikit-learnにあるirisデータの使い方をまとめる。

データの取得とデータ構造

Pythonで扱う場合、scikit-learnのdatasetsモジュールにあるload_iris()でデータを取得できる。データはBunchクラスのオブジェクトととのことだが、通常の扱い方は辞書と同じようだ。

from sklearn.datasets import load_iris

iris_dataset = load_iris()

for key, value in zip(iris_dataset.keys(), iris_dataset.values()):
    print("{}:\n{}\n".format(key, value))

from sklearn.datasets import load_iris

iris_dataset = load_iris()

for key, value in zip(iris_dataset.keys(), iris_dataset.values()):

print("{}:\n{}\n".format(key, value))

データの構造は辞書型で、150個体のアヤメに関する特徴量の配列と各個体の種類、種類名などが格納されている。

data:
[[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 .....
 [6.5 3.  5.2 2. ]
 [6.2 3.4 5.4 2.3]
 [5.9 3.  5.1 1.8]]

target:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

target_names:
['setosa' 'versicolor' 'virginica']

DESCR:
.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

feature_names:
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

filename:
C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\iris.csv

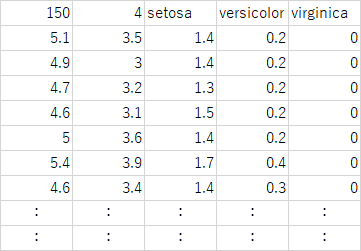
data:

[[5.1 3.5 1.4 0.2]

[4.9 3. 1.4 0.2]

[4.7 3.2 1.3 0.2]

.....

[6.5 3. 5.2 2. ]

[6.2 3.4 5.4 2.3]

[5.9 3. 5.1 1.8]]

target:

[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

2 2]

target_names:

['setosa' 'versicolor' 'virginica']

DESCR:

.. _iris_dataset:

Iris plants dataset

--------------------

**Data Set Characteristics:**

:Number of Instances: 150 (50 in each of three classes)

:Number of Attributes: 4 numeric, predictive attributes and the class

:Attribute Information:

- sepal length in cm

- sepal width in cm

- petal length in cm

- petal width in cm

- class:

- Iris-Setosa

- Iris-Versicolour

- Iris-Virginica

:Summary Statistics:

============== ==== ==== ======= ===== ====================

Min Max Mean SD Class Correlation

============== ==== ==== ======= ===== ====================

sepal length: 4.3 7.9 5.84 0.83 0.7826

sepal width: 2.0 4.4 3.05 0.43 -0.4194

petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)

petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)

============== ==== ==== ======= ===== ====================

:Missing Attribute Values: None

:Class Distribution: 33.3% for each of 3 classes.

:Creator: R.A. Fisher

:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)

:Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken

from Fisher's paper. Note that it's the same as in R, but not as in the UCI

Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the

pattern recognition literature. Fisher's paper is a classic in the field and

is referenced frequently to this day. (See Duda & Hart, for example.) The

data set contains 3 classes of 50 instances each, where each class refers to a

type of iris plant. One class is linearly separable from the other 2; the

latter are NOT linearly separable from each other.

.. topic:: References

- Fisher, R.A. "The use of multiple measurements in taxonomic problems"

Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to

Mathematical Statistics" (John Wiley, NY, 1950).

- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.

(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.

- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System

Structure and Classification Rule for Recognition in Partially Exposed

Environments". IEEE Transactions on Pattern Analysis and Machine

Intelligence, Vol. PAMI-2, No. 1, 67-71.

- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions

on Information Theory, May 1972, 431-433.

- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II

conceptual clustering system finds 3 classes in the data.

- Many, many more ...

feature_names:

['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

filename:

C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\iris.csv

データのキーは以下のようになっている。

from sklearn.datasets import load_iris

iris_dataset = load_iris()

print(iris_dataset.keys())

# dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])

from sklearn.datasets import load_iris

iris_dataset = load_iris()

print(iris_dataset.keys())

# dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])

データの内容

`'data'`～特徴量データセット

150個体のアヤメに関する、4つの特徴量をレコードとしたデータセット。各個体の4つの特徴量の配列を要素とした2次元配列。列のインデックス(0, 1, 2, 3)が四つの特徴量に対応している。

'data': array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       .....
       [6.7, 3. , 5.2, 2.3],
       [6.3, 2.5, 5. , 1.9],
       [6.5, 3. , 5.2, 2. ],
       [6.2, 3.4, 5.4, 2.3],
       [5.9, 3. , 5.1, 1.8]])

'data': array([[5.1, 3.5, 1.4, 0.2],

[4.9, 3. , 1.4, 0.2],

[4.7, 3.2, 1.3, 0.2],

[4.6, 3.1, 1.5, 0.2],

[5. , 3.6, 1.4, 0.2],

.....

[6.7, 3. , 5.2, 2.3],

[6.3, 2.5, 5. , 1.9],

[6.5, 3. , 5.2, 2. ],

[6.2, 3.4, 5.4, 2.3],

[5.9, 3. , 5.1, 1.8]])

`'target'`～アヤメの種類に対応したコード

3種類のアヤメに対応した0～2のコードの配列。150個体のアヤメに対応した1次元配列。

'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

`'target_names'`～アヤメの種類名

アヤメの3つの種類の種類名。stosaは「ヒオウギアヤメ」といって少し大人締めの色形だが、versicolorとvirginicaは素人にはその違いがよく分からない。

'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),

1	'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),

種類名とコードの関係は以下の通り。

setosa	0
versicolor	1
virginica	2

`'feature_names'`～特徴名

データの格納順はDESCRの後。アヤメの種類のクラス分けに使う特徴。

sepal(萼)とpetal(花弁)の長さと幅、計4つの特徴の名称が、単位cmを含む文字列で格納されている。

‘sepal length (cm)’　萼の長さ
‘sepal width (cm)’　萼の幅
‘petal length (cm)’　花弁の長さ
‘petal width (cm)’　花弁の幅

'feature_names': ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

1	'feature_names': ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

特徴名とコードの関係は以下の通り。

sepal length (cm)	0
sepal width (cm)	1
petal length (cm)	2
petal width (cm)	3

`'filename'`～ファイル名

これも格納順はDESCRの後で、CSVファイルの位置が示されている。1行目にはデータ数、特徴量数、特徴量名称が並んでおり、その後に150行のアヤメの個体に対する4列の特徴量と1列の種類データが格納されている。このファイルにはfeature_namesやDESCRに当たるデータは格納されていない。

'filename': 'C:...lib\\site-packages\\sklearn\\datasets\\data\\iris.csv'

1	'filename': 'C:...lib\\site-packages\\sklearn\\datasets\\data\\iris.csv'

`'DESCR'`～データセットの説明

データセットの説明。print(iris_dataset['DESCR'])のようにprint文で整形表示される。

レコード数は150個(3つのクラスで50個ずつ)
属性は、4つの数値属性とクラス(種類)
→predictiveの意味とclassが単数形なのがわからない

.. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
    :Number of Attributes: 4 numeric, predictive attributes and the class
    :Attribute Information:
        - sepal length in cm
        - sepal width in cm
        - petal length in cm
        - petal width in cm
        - class:
                - Iris-Setosa
                - Iris-Versicolour
                - Iris-Virginica
                
    :Summary Statistics:

    ============== ==== ==== ======= ===== ====================
                    Min  Max   Mean    SD   Class Correlation
    ============== ==== ==== ======= ===== ====================
    sepal length:   4.3  7.9   5.84   0.83    0.7826
    sepal width:    2.0  4.4   3.05   0.43   -0.4194
    petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
    petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
    ============== ==== ==== ======= ===== ====================

    :Missing Attribute Values: None
    :Class Distribution: 33.3% for each of 3 classes.
    :Creator: R.A. Fisher
    :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
    :Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.

.. topic:: References

   - Fisher, R.A. "The use of multiple measurements in taxonomic problems"
     Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
     Mathematical Statistics" (John Wiley, NY, 1950).
   - Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
     (Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.
   - Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
     Structure and Classification Rule for Recognition in Partially Exposed
     Environments".  IEEE Transactions on Pattern Analysis and Machine
     Intelligence, Vol. PAMI-2, No. 1, 67-71.
   - Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactions
     on Information Theory, May 1972, 431-433.
   - See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS II
     conceptual clustering system finds 3 classes in the data.
   - Many, many more ...

.. _iris_dataset:

Iris plants dataset

--------------------

**Data Set Characteristics:**

:Number of Instances: 150 (50 in each of three classes)

:Number of Attributes: 4 numeric, predictive attributes and the class

:Attribute Information:

- sepal length in cm

- sepal width in cm

- petal length in cm

- petal width in cm

- class:

- Iris-Setosa

- Iris-Versicolour

- Iris-Virginica

:Summary Statistics:

============== ==== ==== ======= ===== ====================

Min Max Mean SD Class Correlation

============== ==== ==== ======= ===== ====================

sepal length: 4.3 7.9 5.84 0.83 0.7826

sepal width: 2.0 4.4 3.05 0.43 -0.4194

petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)

petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)

============== ==== ==== ======= ===== ====================

:Missing Attribute Values: None

:Class Distribution: 33.3% for each of 3 classes.

:Creator: R.A. Fisher

:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)

:Date: July, 1988

The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken

from Fisher's paper. Note that it's the same as in R, but not as in the UCI

Machine Learning Repository, which has two wrong data points.

This is perhaps the best known database to be found in the

pattern recognition literature. Fisher's paper is a classic in the field and

is referenced frequently to this day. (See Duda & Hart, for example.) The

data set contains 3 classes of 50 instances each, where each class refers to a

type of iris plant. One class is linearly separable from the other 2; the

latter are NOT linearly separable from each other.

.. topic:: References

- Fisher, R.A. "The use of multiple measurements in taxonomic problems"

Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to

Mathematical Statistics" (John Wiley, NY, 1950).

- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.

(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.

- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System

Structure and Classification Rule for Recognition in Partially Exposed

Environments". IEEE Transactions on Pattern Analysis and Machine

Intelligence, Vol. PAMI-2, No. 1, 67-71.

- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions

on Information Theory, May 1972, 431-433.

- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II

conceptual clustering system finds 3 classes in the data.

- Many, many more ...

データの利用

データの取得方法

irisデータセットから各データを取り出すのに、以下の2つの方法がある。

辞書のキーを使って呼び出す（例：iris_dataset['DESCR']）
キーの文字列をプロパティーに指定する（例：iris_dataset.DESCR）

全レコードの特徴量データの取得

'data'から、150の個体に関する4つの特徴量が150行4列の2次元配列で得られる。4つの特徴量は’feature_names’の4つの特徴名に対応している。

from sklearn.datasets import load_iris

iris_data = load_iris()

X = iris_data['data']

print(X)

# [[5.1 3.5 1.4 0.2]
#  [4.9 3.  1.4 0.2]
#  [4.7 3.2 1.3 0.2]
#  .....
#  [6.5 3.  5.2 2. ]
#  [6.2 3.4 5.4 2.3]
#  [5.9 3.  5.1 1.8]]

from sklearn.datasets import load_iris

iris_data = load_iris()

X = iris_data['data']

print(X)

# [[5.1 3.5 1.4 0.2]

# [4.9 3. 1.4 0.2]

# [4.7 3.2 1.3 0.2]

# .....

# [6.5 3. 5.2 2. ]

# [6.2 3.4 5.4 2.3]

# [5.9 3. 5.1 1.8]]

特定の特徴量のデータのみ取得

特定の特徴量に関する全個体のデータを取り出すときにはX[:, n]の形で指定する。

from sklearn.datasets import load_iris

iris_data = load_iris()

features = iris_data['feature_names']
X = iris_data['data']
n_feature = 2

feature = X[:, n_feature]

print("feature name : {}".format(features[n_feature]))
print("feature data :\n{}".format(feature))

# feature name : petal length (cm)
# feature data :
# [1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 1.5 1.6 1.4 1.1 1.2 1.5 1.3 1.4
#  .....
#  5.7 5.2 5.  5.2 5.4 5.1]

from sklearn.datasets import load_iris

iris_data = load_iris()

features = iris_data['feature_names']

X = iris_data['data']

n_feature = 2

feature = X[:, n_feature]

print("feature name : {}".format(features[n_feature]))

print("feature data :\n{}".format(feature))

# feature name : petal length (cm)

# feature data :

# [1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 1.5 1.6 1.4 1.1 1.2 1.5 1.3 1.4

# .....

# 5.7 5.2 5. 5.2 5.4 5.1]

特定のクラスのデータのみ抽出

特定のクラス（この場合は種類）のレコードのみを抽出する方法。ndarrayの条件による要素抽出を使う。

from sklearn.datasets import load_iris

iris_data = load_iris()

targets = iris_data['target_names']
features = iris_data['feature_names']
X = iris_data['data']
y = iris_data['target']

n_class = 1
data_1 = X[y==1]

print("data for class {}:\n{}".format(targets[n_class], X[y==n_class]))

# data for class versicolor:
# [[7.  3.2 4.7 1.4]
#  [6.4 3.2 4.5 1.5]
#  [6.9 3.1 4.9 1.5]
#  .....
#  [6.2 2.9 4.3 1.3]
#  [5.1 2.5 3.  1.1]
#  [5.7 2.8 4.1 1.3]]

from sklearn.datasets import load_iris

iris_data = load_iris()

targets = iris_data['target_names']

features = iris_data['feature_names']

X = iris_data['data']

y = iris_data['target']

n_class = 1

data_1 = X[y==1]

print("data for class {}:\n{}".format(targets[n_class], X[y==n_class]))

# data for class versicolor:

# [[7. 3.2 4.7 1.4]

# [6.4 3.2 4.5 1.5]

# [6.9 3.1 4.9 1.5]

# .....

# [6.2 2.9 4.3 1.3]

# [5.1 2.5 3. 1.1]

# [5.7 2.8 4.1 1.3]]

2次元で配置されたAxesを一括で扱う

2020-03-08 / tau / コメントする

subplots()やadd_subplot()で複数の行数・列数のAxesを生成すると、Axesオブジェクトの2次元の配列となる。

この結果に対して一律に処理をしたい場合（たとえば軸の値や凡例を設定したい、アスペクトを揃えたいなどの場合）、いちいち二重ループを回すのが面倒。

import numpy as np
import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

x = np.linspace(-np.pi, np.pi)
n = 1
for row in axs:
    for ax in row:
        ax.plot(x, np.sin(n*x), label="n={}".format(n))
        n += 1
        ax.set_ylim(-1.2, 1.8)
        ax.legend(loc='upper left')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

x = np.linspace(-np.pi, np.pi)

n = 1

for row in axs:

for ax in row:

ax.plot(x, np.sin(n*x), label="n={}".format(n))

n += 1

ax.set_ylim(-1.2, 1.8)

ax.legend(loc='upper left')

plt.show()

これを1次元配列に変換して一括で扱う方法。

変換方法の1つは、以下のように1次元配列で取り出してしまう方法

axs_1d = [ax for row in axs for ax in row]

1	axs_1d = [ax for row in axs for ax in row]

あるいは、以下のように2次元配列を1次元に変換する方法（当初、reshape(1, -1)[0]のようなことをしていたが、reshape(-1)とすればよいことがわかった）。

axs_1d = axs.reshape(-1)

1	axs_1d = axs.reshape(-1)

こうすると1次元配列axs_1dで2次元のaxsの全要素に対してアクセス可能になる。

import numpy as np
import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

axs_1d = axs.reshape(-1)

x = np.linspace(-np.pi, np.pi)
for n, ax in enumerate(axs_1d):
    ax.plot(x, np.sin(n*x), label="n={}".format(n))
    ax.set_ylim(-1.2, 1.8)
    ax.legend(loc='upper left')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

fig, axs = plt.subplots(2, 2)

axs_1d = axs.reshape(-1)

x = np.linspace(-np.pi, np.pi)

for n, ax in enumerate(axs_1d):

ax.plot(x, np.sin(n*x), label="n={}".format(n))

ax.set_ylim(-1.2, 1.8)

ax.legend(loc='upper left')

plt.show()

このほかにflatten()、ravel()を使う方法もある。flatten()はコピーを返すが、Axesオブジェクトへの参照先は変わらないので同じ効果。

各グラフにカウンターの値を適用するときはenumerate、他のリストなどと同時に変えていくときはzipを使う。

matplotlib.pyplot.hist – ヒストグラム

2020-03-08 / tau / コメントする

概要

matplotlib.pyplot.histは、配列データのヒストグラムを描画する。主なパラメータのみ示す。

hist(X, bins, range, density, cumulative, histtype, rwidth, color, stacked): Xはヒストグラムのデータで一つのグラフに一つの1次元配列。その他のパラメーターは以下で説明。

ヒストグラムの形式

度数分布

1次元の配列でデータを渡すと、その度数分布が描かれる。

ただしデフォルトでは各ビンのエッジが区別できないため、これを描くためにはedghecolorの指定が必要。edgecolorの代わりにecで指定してもよい。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x)
axs[1].hist(x, edgecolor='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x)

axs[1].hist(x, edgecolor='k')

plt.show()

頻度分布

density=Trueを指定すると、頻度分布になる。各ビンの総和が1となるように調整され、形状は度数分布と同じ。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, ec='k')
axs[1].hist(x, density=True, ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, ec='k')

axs[1].hist(x, density=True, ec='k')

plt.show()

累積分布図

cumulative=Trueを指定すると、累積度数分布、累積頻度分布を描く。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, cumulative=True, ec='k')
axs[1].hist(x, cumulative=True, density=True, ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x, cumulative=True, ec='k')

axs[1].hist(x, cumulative=True, density=True, ec='k')

plt.show()

ビン数

binsでヒストグラムの柱（ビン）の数等を指定する。デフォルトはbins=10。

bins=n: ビンの数を数値で指定する。
bins=sequence: ビンの境界値をリスト等で指定する。

ビン(bin)は英語で、店の商品や工場の部品などを入れておく大きなケース、ストッカーのことをいい、British Englishではごみ箱を指す。日本語の瓶(びん)の呼び名とは関係ないらしい。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, bins=5, ec='k')
axs[1].hist(x, bins=[-3, -2, -1, 0, 0.5, 1, 1.5, 2], ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, bins=5, ec='k')

axs[1].hist(x, bins=[-3, -2, -1, 0, 0.5, 1, 1.5, 2], ec='k')

plt.show()

レンジ

rangeでヒストグラムのビンを分割する範囲を指定する。そのレンジの上下限値の間でbinsで指定されたビンに分割される。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, edgecolor='k')
axs[1].hist(x, range=(-3, 3), ec='k')
axs[2].hist(x, range=(-1.5, 1.5), ec='k')

for ax in axs:
    ax.set_xlim(-3, 3)
    ax.set_xticks(np.arange(-3, 4, 1))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, edgecolor='k')

axs[1].hist(x, range=(-3, 3), ec='k')

axs[2].hist(x, range=(-1.5, 1.5), ec='k')

for ax in axs:

ax.set_xlim(-3, 3)

ax.set_xticks(np.arange(-3, 4, 1))

plt.show()

色・エッジの指定

colorでビンの色、edgecolor/ecでエッジの色、linewidthでエッジの幅を指定する。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, color='lightseagreen', edgecolor='k')
axs[1].hist(x, color='lightcoral', ec='navy', linewidth=3)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, color='lightseagreen', edgecolor='k')

axs[1].hist(x, color='lightcoral', ec='navy', linewidth=3)

plt.show()

ビンの幅

rwidthでビンの幅を指定する。デフォルトはrwidth=1で各ビンが密着。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, rwidth=0.8, ec='k')
axs[1].hist(x, bins=13, width=1.2, ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(6.4, 2.4))

axs[0].hist(x, rwidth=0.8, ec='k')

axs[1].hist(x, bins=13, width=1.2, ec='k')

plt.show()

ヒストグラムのタイプ

histtype='type'でヒストグラムのタイプを指定する。

bar: 一般的なヒストグラムの形状。
barstacked: 複数のヒストグラムの場合に、同じビンの値を積み上げていく。
step: ビンの間の境界を描かない。
stepfilled: ビンの間の境界を描かず、中を塗りつぶす。

以下の例では、'bar'、'step'、'stepfilled'について例示。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, histtype='bar', ec='k')
axs[1].hist(x, histtype='step', ec='k')
axs[2].hist(x, histtype='stepfilled', ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, axs = plt.subplots(1, 3, figsize=(9.6, 2.4))

axs[0].hist(x, histtype='bar', ec='k')

axs[1].hist(x, histtype='step', ec='k')

axs[2].hist(x, histtype='stepfilled', ec='k')

plt.show()

複数のヒストグラム

単純な重ね合わせ

複数のヒストグラムを重ね合わせるには、同じターゲットに対して各データについてhistを実行する。

単に重ね合わせると、初めの方のヒストグラムが後の方で塗りつぶされてしまうので、それらを見えるようにするにはalphaで透明度を指定する。

ただし単に重ね合わせただけの場合、各ヒストグラムのビンの境界が必ずしも一致しない。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, color='c', edgecolor='k')
axs[0].hist(x2, color='m', edgecolor='k')
axs[0].hist(x3, color='g', edgecolor='k')

axs[1].hist(x1, color='c', edgecolor='k', alpha=0.5)
axs[1].hist(x2, color='m', edgecolor='k', alpha=0.5)
axs[1].hist(x3, color='g', edgecolor='k', alpha=0.5)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, color='c', edgecolor='k')

axs[0].hist(x2, color='m', edgecolor='k')

axs[0].hist(x3, color='g', edgecolor='k')

axs[1].hist(x1, color='c', edgecolor='k', alpha=0.5)

axs[1].hist(x2, color='m', edgecolor='k', alpha=0.5)

axs[1].hist(x3, color='g', edgecolor='k', alpha=0.5)

plt.show()

ヒストグラムとplotの重ね合わせ

こちらを参照。

ビン境界の整合

複数のヒストグラムのビンの境界を一致させるには以下の方法がある。

各グラフに対して同じrangeとbins=nを指定する
各グラフに対して同じbins=sequenceを指定する

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, range=(-4, 4), bins=20, color='c', ec='k', alpha=0.5)
axs[0].hist(x2, range=(-4, 4), bins=20, color='m', ec='k', alpha=0.5)
axs[0].hist(x3, range=(-4, 4), bins=20, color='g', ec='k', alpha=0.5)

bn = np.linspace(-4, 4, 21)
axs[1].hist(x1, bins=bn, color='c', ec='k', alpha=0.5)
axs[1].hist(x2, bins=bn, color='m', ec='k', alpha=0.5)
axs[1].hist(x3, bins=bn, color='g', ec='k', alpha=0.5)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

fig, axs = plt.subplots(1,2, figsize=(6.4, 2.4))

axs[0].hist(x1, range=(-4, 4), bins=20, color='c', ec='k', alpha=0.5)

axs[0].hist(x2, range=(-4, 4), bins=20, color='m', ec='k', alpha=0.5)

axs[0].hist(x3, range=(-4, 4), bins=20, color='g', ec='k', alpha=0.5)

bn = np.linspace(-4, 4, 21)

axs[1].hist(x1, bins=bn, color='c', ec='k', alpha=0.5)

axs[1].hist(x2, bins=bn, color='m', ec='k', alpha=0.5)

axs[1].hist(x3, bins=bn, color='g', ec='k', alpha=0.5)

plt.show()

並べる・積み上げる

複数のデータを配列とした場合（複数の1次元のデータを並べて2次元配列として与えた場合）、デフォルトでは各ビンが横に並べられる。

また、stacked=Trueあるいはhisttype='barstacked'を指定した場合、同じ階級のビンが積み上げられる。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)
X = [x1, x2, x3]

fig, axs = plt.subplots(1,3, figsize=(9.6, 2.4))

axs[0].hist(X, bins=20, ec='k')
axs[1].hist(X, bins=20, stacked=True, ec='k')
axs[2].hist(X, bins=20, histtype='barstacked', ec='k')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

X = [x1, x2, x3]

fig, axs = plt.subplots(1,3, figsize=(9.6, 2.4))

axs[0].hist(X, bins=20, ec='k')

axs[1].hist(X, bins=20, stacked=True, ec='k')

axs[2].hist(X, bins=20, histtype='barstacked', ec='k')

plt.show()

戻り値

n: 各ビンの値(度数または頻度)
bins: 各ビンの境界値
patches: ヒストグラム描画に使われたpatcheオブジェクトのリスト

単一のヒストグラムの場合

以下の例では、nの結果として10個のビンの度数が得られている。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, ax = plt.subplots(1, 1, figsize=(6.4, 2.4))

n, bins, patches = ax.hist(x)

print(n)
print(bins)
print(patches)

plt.show()

# [0.02073508 0.10367541 0.14514557 0.26955606 0.35249639 0.37323147
#  0.33176131 0.2280859  0.14514557 0.10367541]
# [-2.55298982 -2.07071537 -1.58844093 -1.10616648 -0.62389204 -0.1416176
#   0.34065685  0.82293129  1.30520574  1.78748018  2.26975462]
# <a list of 10 Patch objects>

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x = np.random.normal(0, 1, 100)

fig, ax = plt.subplots(1, 1, figsize=(6.4, 2.4))

n, bins, patches = ax.hist(x)

print(n)

print(bins)

print(patches)

plt.show()

# [0.02073508 0.10367541 0.14514557 0.26955606 0.35249639 0.37323147

# 0.33176131 0.2280859 0.14514557 0.10367541]

# [-2.55298982 -2.07071537 -1.58844093 -1.10616648 -0.62389204 -0.1416176

# 0.34065685 0.82293129 1.30520574 1.78748018 2.26975462]

# <a list of 10 Patch objects>

複数のヒストグラムの配列の場合

複数のデータを配列で与えた場合の戻り値。nが3つのデータごとの配列になっている。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)
x2 = np.random.normal(0, 1, 500)
x3 = np.random.normal(2, 1, 500)
X = [x1, x2, x3]

fig, ax = plt.subplots(1,1, figsize=(3.2, 2.4))

n, bins, patches = ax.hist(X, bins=20, ec='k')

print(n)
print(bins)
print(patches)

plt.show()

# [array([ 6., 10., 34., 59., 98., 92., 87., 62., 24., 20.,  8.,  0.,  0.,
#         0.,  0.,  0.,  0.,  0.,  0.,  0.]), array([ 0.,  0.,  0.,  2.,  5., 12., 33., 64., 89., 99., 89., 55., 33.,
#        12.,  6.,  1.,  0.,  0.,  0.,  0.]), array([  0.,   0.,   0.,   0.,   0.,   0.,   0.,   2.,   2.,  11.,  27.,
#         54.,  89.,  89., 106.,  66.,  34.,  12.,   6.,   2.])]
# [-4.77259276 -4.27541438 -3.778236   -3.28105763 -2.78387925 -2.28670087
#  -1.7895225  -1.29234412 -0.79516574 -0.29798737  0.19919101  0.69636938
#   1.19354776  1.69072614  2.18790451  2.68508289  3.18226127  3.67943964
#   4.17661802  4.6737964   5.17097477]
# <a list of 3 Lists of Patches objects>

import numpy as np

import matplotlib.pyplot as plt

np.random.seed(0)

x1 = np.random.normal(-2, 1, 500)

x2 = np.random.normal(0, 1, 500)

x3 = np.random.normal(2, 1, 500)

X = [x1, x2, x3]

fig, ax = plt.subplots(1,1, figsize=(3.2, 2.4))

n, bins, patches = ax.hist(X, bins=20, ec='k')

print(n)

print(bins)

print(patches)

plt.show()

# [array([ 6., 10., 34., 59., 98., 92., 87., 62., 24., 20., 8., 0., 0.,

# 0., 0., 0., 0., 0., 0., 0.]), array([ 0., 0., 0., 2., 5., 12., 33., 64., 89., 99., 89., 55., 33.,

# 12., 6., 1., 0., 0., 0., 0.]), array([ 0., 0., 0., 0., 0., 0., 0., 2., 2., 11., 27.,

# 54., 89., 89., 106., 66., 34., 12., 6., 2.])]

# [-4.77259276 -4.27541438 -3.778236 -3.28105763 -2.78387925 -2.28670087

# -1.7895225 -1.29234412 -0.79516574 -0.29798737 0.19919101 0.69636938

# 1.19354776 1.69072614 2.18790451 2.68508289 3.18226127 3.67943964

# 4.17661802 4.6737964 5.17097477]

# <a list of 3 Lists of Patches objects>

二項分布

2020-03-01 / tau / コメントする

概要

ある試行において起こり得る事象が2通りしかない場合、このような試行をベルヌーイ試行(Bernoulli trial)という。たとえばコインを投げた時に表が出るか裏が出るか、くじ引きを引いたときに当たりが出るかはずれが出るか、など。

ベルヌーイ試行の2つの事象を確率変数 $X = 1, 0$ で表し、 $X = 1$ となる確率が $p$ であるとする。

(1) $\begin{alignat*}{1} P(X=1) &= p \\ P(X=0) &= 1-p \end{alignat*}$

このようなベルヌーイ試行を $n$ 回繰り返したとき、 $X=1$ が生じる回数の確率分布が二項分布(Binomial distribution)で、 $B(n, p)$ のように表示される。二項分布の例には以下のようなものがある。

コインの表／裏が出る確率が等しく1/2のとき、このコインを10回投げた時に表がでる回数の分布
打率3割の打者が4回打席に立って2安打以上打つ確率

確率分布

$n$ 回のベルヌーイ試行のうち、 $X=1$ が $k$ 回起こるケースは、 ${}_n \mathrm{C}_k$ 通りなので、二項分布の確率は以下のように表せる。

(2) $\begin{equation*} P(X=k ; p) = {}_n \mathrm{C}_k p^k (1-p)^{n-k} \end{equation*}$

全事象

$k=0~n$ の確率の和が全事象の確率であり、二項定理から、

(3) $\begin{equation*} \sum_{k=0}^n {}_n \mathrm{C}_k p^k (1-p)^{n-k} = (p + 1 - p)^n = 1 \end{equation*}$

平均と分散

二項分布 $B(n, p)$ の平均と分散は、以下のようになる。

(4) $\begin{alignat*}{1} E(X) &= np \\ V(X) &= np(1-p) \end{alignat*}$

この導出において興味深いテクニックが使われる。

二項分布の形

$n=20, p=0.3$ の二項分布のグラフをPythonで描くと以下のようになる。

import numpy as np
from scipy.stats import binom
from scipy.stats import norm
import matplotlib.pyplot as plt

np.random.seed(0)

n = 20
p = 0.3

min_k = 0
max_k = n

data = np.random.binomial(n, p, size=100)

k = np.arange(min_k, max_k + 1)
binom_pmf = binom.pmf(k, n, p)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.plot(k, binom_pmf, label="binomial PMF")
ax.hist(data, bins=20, range=(min_k, max_k), density=True,
    color='c', edgecolor='k', label="binomial trials")
ax.legend(loc="upper right")
ax.text(15, 0.175, "n={}".format(n))
ax.text(15, 0.165, "p={}".format(p))

plt.show()

import numpy as np

from scipy.stats import binom

from scipy.stats import norm

import matplotlib.pyplot as plt

np.random.seed(0)

n = 20

p = 0.3

min_k = 0

max_k = n

data = np.random.binomial(n, p, size=100)

k = np.arange(min_k, max_k + 1)

binom_pmf = binom.pmf(k, n, p)

fig = plt.figure()

ax = fig.add_subplot(111)

ax.plot(k, binom_pmf, label="binomial PMF")

ax.hist(data, bins=20, range=(min_k, max_k), density=True,

color='c', edgecolor='k', label="binomial trials")

ax.legend(loc="upper right")

ax.text(15, 0.175, "n={}".format(n))

ax.text(15, 0.165, "p={}".format(p))

plt.show()

正規分布近似

二項分布 $B(n, p)$ は、 $np, np(1-p)$ が十分大きいとき(具体的には5より大きいとき)、平均 $np$ 、分散 $np(1-p)$ の正規分布で近似できる(ド・モアブル－ラプラスの定理)。

(5) $\begin{equation*} X \sim B(n, p) \rightarrow \frac{X - np}{\sqrt{np(1-p)}} \sim N=(0, 1) \end{equation*}$

これは、二項分布の1回の試行において成功する場合をX_i = 1、失敗する場合をX_i = 0として、成功回数 $\sum X_i$ の平均と分散がnp, np(1 − p)であることからわかる。

以下は、 $n, p$ の3つずつの組み合わせに対する、二項分布と正規分布の一致具合を比べたもの。表示範囲は、正規分布とみなしたときの $-3\sigma \sim 3\sigma$ に対応する範囲で設定している。

import numpy as np
from scipy.stats import binom
from scipy.stats import norm
import matplotlib.pyplot as plt

np.random.seed(0)

fig = plt.figure(figsize=(12, 9))
fig.subplots_adjust(hspace=0.3)

n_subplot = 0
for n in [10, 100, 1000]:
    for p in [0.15, 0.3, 0.5]:
        n_subplot += 1
        k = np.arange(0, n + 1)
        mu = n * p
        sig = np.sqrt(n * p * (1 - p))
        binom_pmf = binom.pmf(k, n, p)
        norm_pdf = norm.pdf(k, loc=mu, scale=sig)

        ax = fig.add_subplot(3, 3, n_subplot)
        ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig))
        ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF")
        ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF")
        ax.legend(loc="lower center", fontsize=8)
        ax.set_title("n={}, p={:.2f}%".format(n, p))

plt.show()

import numpy as np

from scipy.stats import binom

from scipy.stats import norm

import matplotlib.pyplot as plt

np.random.seed(0)

fig = plt.figure(figsize=(12, 9))

fig.subplots_adjust(hspace=0.3)

n_subplot = 0

for n in [10, 100, 1000]:

for p in [0.15, 0.3, 0.5]:

n_subplot += 1

k = np.arange(0, n + 1)

mu = n * p

sig = np.sqrt(n * p * (1 - p))

binom_pmf = binom.pmf(k, n, p)

norm_pdf = norm.pdf(k, loc=mu, scale=sig)

ax = fig.add_subplot(3, 3, n_subplot)

ax.set_xlim(np.ceil(mu - 3*sig), np.floor(mu + 3*sig))

ax.plot(k, binom_pmf, color='y', linewidth=7, label="binomial PMF")

ax.plot(k, norm_pdf, color='k', linewidth=2, label="normal PDF")

ax.legend(loc="lower center", fontsize=8)

ax.set_title("n={}, p={:.2f}%".format(n, p))

plt.show()

母集団確率の最尤推定

二項分布の母集団確率の最尤推定量は $p=k/n$ である。

実用例

適用例

二項確率が与えられたときの、発生回数や個体数の予測。

当たりの確率がpの掛けの、掛け回数nと当たりの回数k
故障率pの部品について、n個の部品のうちの故障数k
罹患率pの病気について、n人のうちの罹患者数k
支持率pの政党に対して、n人のうちの支持者数k

分析例

上記と逆に、nサンプルから事象がk回発生したときの確率を推定。

尤度・最尤推定

2020-03-01 / tau / コメントする

コインの例

最尤推定法(maximum likelihood estimation)は確率分布 $f_D$ のパラメーター $\theta$ を、その母集団から得られたサンプルから推定する方法。

たとえば、表の出る確率が必ずしも1/2でないコインを50回投げた時、表が15回出たとすると、このコインの表が出る確率はいくらか、といった問題。20～30回くらいの間だと普通のコインで表／裏の確率は1/2かなと思うが、50回投げて表が15回しかでないとちょっと疑いたくなる。

ここで、表が出る確率を $p$ として、 $n$ 回の試行中表が $k$ 回出る確率は以下の通り。

(1) $\begin{equation*} P(k:n\,|\,p) = \binom{n}{k} p^k (1-p)^{n-k} \end{equation*}$

先の問題の結果について、母集団の確率をいくつか仮定して計算してみると

(2) $\begin{equation*} \begin{align} p &= 1/2 \quad \rightarrow \quad P(15:50\,|\,0.5) \approx 0.002 \\ p &= 1/3 \quad \rightarrow \quad P(15:50\,|\,0.3) \approx 0.107 \\ p &= 1/4 \quad \rightarrow \quad P(15:50\,|\,0.1) \approx 0.089 \end{align} \end{equation*}$

得られたサンプルの下では、少なくともぼ表が出る確率を1/2や1/4と考えるよりは、1/3と考えた方がこのサンプルのパターンが発生する確率が高い。

そこで、サンプルのパターンに対して母集団の確率を変化させてみると、以下のようになる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom

n = 50
k = 15
p = np.linspace(0, 1, 100)

fig, ax = plt.subplots(figsize=(4.8, 3.6))

ax.plot(p, binom.pmf(k, n, p), c='navy')
ax.plot((k/n, k/n), (0, binom.pmf(k, n, k/n)), c='gray', linestyle='dashed')

ax.set_xlim(0, 1)
ax.set_ylim(0, 0.15)
ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from scipy.stats import binom

n = 50

k = 15

p = np.linspace(0, 1, 100)

fig, ax = plt.subplots(figsize=(4.8, 3.6))

ax.plot(p, binom.pmf(k, n, p), c='navy')

ax.plot((k/n, k/n), (0, binom.pmf(k, n, k/n)), c='gray', linestyle='dashed')

ax.set_xlim(0, 1)

ax.set_ylim(0, 0.15)

ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

グラフ上は、母集団確率が15/50=0.3のときにサンプルパターンの発生確率が最も高くなっている。

解析的に確率が最大となる母集団確率を求めるために、式(1)を $p$ で微分してゼロとなる点を求める。

(3) $\begin{gather*} \frac{d P(k:n\,|\,p)}{dp} = \binom{n}{k}\left(kp^{k-1} (1-p)^{n-k} - p^k (n-k)(1-p)^{n-k-1} \right) = 0 \\ p^{k-1} (1-p)^{n-k-1} \left( k (1-p) - (n-k) p \right) = 0 \\ p^{k-1} (1-p)^{n-k-1} \left( k - np \right) = 0 \end{gather*}$

上式の解は $p = 0, 1, k/n$ となるが、 $p=0, 1$ の場合は式(1)がゼロとなることから、確率が最大となるのは $p=k/n$ であることがわかる。

尤度関数と最尤法

母集団の確率分布を $f$ 、母集団のパラメータを $\theta$ 、得られたサンプルセットを $x_1, \ldots, x_n$ とすると、パラメーターが $\theta$ である確率は

(4) $\begin{equation*} Pr(x_1, \ldots, x_n \,|\, \theta) = f(x_1, \ldots, x_n \,|\, \theta) \end{equation*}$

このとき、パラメーター $\theta$ に関する尤度関数は以下のように定義される。

(5) $\begin{equation*} L(\theta) = f(x_1, \ldots, x_n \,|\, \theta) \end{equation*}$

通常、尤度関数が最大となるパラメーターを求めるためには対数尤度関数が用いられる。

(6) $\begin{equation*} \frac{d}{d \theta} \ln L(\theta) = 0 \end{equation*}$

サンプルの質と尤度

先のコインの問題で、試行数が10回の場合と100回の場合を比べてみる。それぞれについて、表の確率が0.3、0.5、0.7に対応する回数は試行回数が10回の場合は3回、5回、7回、試行回数100回に対しては30回、50回、70回である。それぞれの表の階数に対して、母集団確率の尤度関数を描くと以下のようになる。

import numpy as np
import matplotlib.pyplot as plt
from functools import reduce

def comb(n, k):
    numer = reduce(lambda x,y:x*y, range(n - k + 1, n))
    denom = reduce(lambda x,y:x*y, range(1, k + 1))
    return numer // denom

def binom(n, k, p):
    return comb(n, k) * p**k * (1 - p)**(n - k)

n = [10, 100]
k = [np.array([3, 5, 7]), np.array([30, 50, 70])]

p = np.linspace(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(9.6, 3.6))

for ax, n, k in zip(axs, n, k):
    ax.set_title("n={}".format(n))

    for t in k:
        p_mle = t / n
        prob = binom(n, t, p)

        ax.plot(p, prob, c='navy')
        ax.plot((p_mle, p_mle), (0, binom(n, t, p_mle)), c='gray', linestyle='dashed')

        ax.set_xlim(0, 1)
        ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from functools import reduce

def comb(n, k):

numer = reduce(lambda x,y:x*y, range(n - k + 1, n))

denom = reduce(lambda x,y:x*y, range(1, k + 1))

return numer // denom

def binom(n, k, p):

return comb(n, k) * p**k * (1 - p)**(n - k)

n = [10, 100]

k = [np.array([3, 5, 7]), np.array([30, 50, 70])]

p = np.linspace(0, 1, 100)

fig, axs = plt.subplots(1, 2, figsize=(9.6, 3.6))

for ax, n, k in zip(axs, n, k):

ax.set_title("n={}".format(n))

for t in k:

p_mle = t / n

prob = binom(n, t, p)

ax.plot(p, prob, c='navy')

ax.plot((p_mle, p_mle), (0, binom(n, t, p_mle)), c='gray', linestyle='dashed')

ax.set_xlim(0, 1)

ax.set_xticks(np.arange(0, 1.1, 0.1))

plt.show()

試行回数が100回の場合には分布が尖っており、最尤推定されたパラメーターの確度が高いが、10回の場合には分布がなだらかで、最尤推定された値以外のパラメーターの確率も高くなっている。

最尤推定の場合、サンプルの規模が推定値の信頼度に関わってくる。

Python3 – 配列要素の重複を除く

2020-02-29 / tau / コメントする

リスト要素の重複を除く

リストをset()関数の引数にすると、重複する要素がなくなり全ての要素がユニークになる。

import random

a = [random.randint(0, 2) for n in range(20)]

print(a)
print(set(a))

# [2, 2, 2, 2, 1, 0, 1, 0, 0, 0, 0, 1, 1, 2, 1, 1, 0, 2, 2, 0]
# {0, 1, 2}

import random

a = [random.randint(0, 2) for n in range(20)]

print(a)

print(set(a))

# [2, 2, 2, 2, 1, 0, 1, 0, 0, 0, 0, 1, 1, 2, 1, 1, 0, 2, 2, 0]

# {0, 1, 2}

ただし結果は集合なので、これをリスト化するにはlist()関数を使う。

set()関数の結果、要素は昇順に並んでいるが、hashの計算方法によって必ずしも昇順になると決まってはいない。そこでsorted()関数でリストをソートしておく(生成されたリストをほかで再利用しないなら、sort()メソッドを使ってもよい)。

import random

a = [random.randint(0, 2) for n in range(20)]

print(a)
print(sorted(list(set(a))))

# [2, 2, 2, 2, 1, 0, 1, 0, 0, 0, 0, 1, 1, 2, 1, 1, 0, 2, 2, 0]
# [0, 1, 2]

import random

a = [random.randint(0, 2) for n in range(20)]

print(a)

print(sorted(list(set(a))))

# [2, 2, 2, 2, 1, 0, 1, 0, 0, 0, 0, 1, 1, 2, 1, 1, 0, 2, 2, 0]

# [0, 1, 2]

ndarrayの要素の重複を除く

元の配列がndarrayで与えられた場合でも、set()関数を適用すると結果は集合となるが、ndarrayの生成時に引数を集合とすると配列として生成されずに集合のまま。

import numpy as np
import numpy.random as rnd

a = rnd.randint(0, 3, 20)

print(a)
print(set(a))
print(np.array(set(a)))

# [2 2 1 2 2 0 1 1 0 1 0 1 2 1 0 1 0 2 2 0]
# {0, 1, 2}
# {0, 1, 2}

import numpy as np

import numpy.random as rnd

a = rnd.randint(0, 3, 20)

print(a)

print(set(a))

print(np.array(set(a)))

# [2 2 1 2 2 0 1 1 0 1 0 1 2 1 0 1 0 2 2 0]

# {0, 1, 2}

そこで、list()関数でいったん集合をリスト化してからndarrayにする必要がある。

また、要素の昇順を保証するためにnp.array()関数でソートしておく。生成した配列を再利用しないのであれば、ndarrayのsort()メソッドを使ってもよい。

import numpy as np
import numpy.random as rnd

a = rnd.randint(0, 3, 20)

print(a)
print(np.array(list(set(a))))

# [2 1 2 0 0 0 2 2 2 1 0 1 0 2 0 0 2 0 2 2]
# [0 1 2]

import numpy as np

import numpy.random as rnd

a = rnd.randint(0, 3, 20)

print(a)

print(np.array(list(set(a))))

# [2 1 2 0 0 0 2 2 2 1 0 1 0 2 0 0 2 0 2 2]

# [0 1 2]

利用例～クラス値を持つデータの分類

たとえば多数のデータの特性値とクラス区分が配列で与えられた場合、クラスごとにマーカーの形や色を変えてプロットするなど、クラスごとに元のデータを分けて処理したい場合。

以下のようにset()関数で重複を除いてループ処理できる。

import numpy as np

X = np.array(['swallow', 'carp', 'dog', 'horse', 'hawk', 'bonito'])
y = np.array([1, 0, 3, 3, 1, 0])

for cls in set(y):
    print(X[y==cls])

# ['carp' 'bonito']
# ['swallow' 'hawk']
# ['dog' 'horse']

import numpy as np

X = np.array(['swallow', 'carp', 'dog', 'horse', 'hawk', 'bonito'])

y = np.array([1, 0, 3, 3, 1, 0])

for cls in set(y):

print(X[y==cls])

# ['carp' 'bonito']

# ['swallow' 'hawk']

# ['dog' 'horse']

Gradient～勾配ベクトル

2020-02-27 / tau / コメントする

定義

多変数の関数のグラジエント(gradient)は勾配とも呼ばれ、以下で定義される。

(1) $\begin{equation*} \nabla f( x_1, \ldots, x_n ) = \left( \frac{\partial f}{\partial x_1} , \ldots , \frac{\partial f}{\partial x_n} \right) = \left( f_{x_1} , \ldots , f_{x_n} \right) \end{equation*}$

2変数の場合

(2) $\begin{equation*} \nabla f( x, y ) = \left( \frac{\partial f}{\partial x} , \ldots , \frac{\partial f}{\partial y} \right) = \left( f_x , \ldots , f_y \right) \end{equation*}$

準備～1変数関数の微分係数

微分係数の符号だけを見た場合

gradientの前に、1変数関数の微分係数についてもう一度考えてみる。

たとえば $y = (x - 1)^2 + 1$ は $x = 1$ で極値を持ち、その前後で微分係数の符号が変わる。

(3) $\begin{equation*} y' = 2(x - 1) \left\{ \begin{align} < 0 \quad (x < 1) \\ = 0 \quad (x = 1) \\ > 0 \quad (x > 1) \end{align} \right. \end{equation*}$

教科書的には、極値をとる点の前後で減少から増加に変わるということになる。

import numpy as np
import matplotlib.pyplot as plt


x_min = -1
x_max = 3

x = np.linspace(x_min, x_max, 50)
y = (x - 1)**2 + 1

n_points = 21
u0 = np.linspace(x_min, x_max, n_points)
u = 2 * (u0 - 1)
zeros = np.zeros(n_points)

fig, ax = plt.subplots()

ax.plot(x, y)
ax.quiver(u0, zeros, zeros, u)

ax.set_xlim(x_min, x_max)
ax.set_ylim(x_min, x_max)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

x_min = -1

x_max = 3

x = np.linspace(x_min, x_max, 50)

y = (x - 1)**2 + 1

n_points = 21

u0 = np.linspace(x_min, x_max, n_points)

u = 2 * (u0 - 1)

zeros = np.zeros(n_points)

fig, ax = plt.subplots()

ax.plot(x, y)

ax.quiver(u0, zeros, zeros, u)

ax.set_xlim(x_min, x_max)

ax.set_ylim(x_min, x_max)

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.set_aspect('equal')

plt.show()

微分係数の符号を方向としてみた場合

同じ微分係数の値を、それが得られる値に対して、符号を考慮して矢印で表してみる。

ただしここでは、矢印の重なりを避けるために、少しずつ縦方向にずらして描いている。

こう描いてみると分かるが、微分係数の正負が方向を表すと考えると、「微分係数は、その方向に関数がどれだけ増加の傾きを持っているか」という意味を持つことがわかる。

import numpy as np
import matplotlib.pyplot as plt


x_min = -1
x_max = 3

x = np.linspace(x_min, x_max, 50)
y = (x - 1)**2 + 1

n_points = 21
u0 = np.linspace(x_min, x_max, n_points)
u = 2 * (u0 - 1)
v0 = np.linspace(-0.5, 0.5, n_points)
zeros = np.zeros(n_points)

fig, ax = plt.subplots()

ax.plot(x, y)
ax.quiver(u0, v0, u, zeros)

ax.set_xlim(x_min, x_max)
ax.set_ylim(x_min, x_max)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

x_min = -1

x_max = 3

x = np.linspace(x_min, x_max, 50)

y = (x - 1)**2 + 1

n_points = 21

u0 = np.linspace(x_min, x_max, n_points)

u = 2 * (u0 - 1)

v0 = np.linspace(-0.5, 0.5, n_points)

zeros = np.zeros(n_points)

fig, ax = plt.subplots()

ax.plot(x, y)

ax.quiver(u0, v0, u, zeros)

ax.set_xlim(x_min, x_max)

ax.set_ylim(x_min, x_max)

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.set_aspect('equal')

plt.show()

微分係数の曲線上での分布

関数の曲線上で、微分係数の方向と大きさを考慮してベクトルを描いてみる。ベクトルの水平方向の成分を微分係数と同じ符号で長さ1、垂直方向の成分を微分係数の絶対値としている。

こうしてみると、微分係数は各位置での関数の増加方向とその増分を表していることがわかる。

import numpy as np
import matplotlib.pyplot as plt


x_min = -1
x_max = 3

x = np.linspace(x_min, x_max, 50)
y = (x - 1)**2 + 1

n_points = 21
u0 = np.linspace(x_min, x_max, n_points)
v0 = (u0 - 1)**2 + 1
v = 2 * (u0 - 1)
u = np.sign(v)
v = np.abs(v)

fig, ax = plt.subplots()

ax.plot(x, y, color='royalblue', alpha=0.5)
ax.quiver(u0, v0, u, v)

ax.set_xlim(x_min, x_max)
ax.set_ylim(x_min, x_max)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

x_min = -1

x_max = 3

x = np.linspace(x_min, x_max, 50)

y = (x - 1)**2 + 1

n_points = 21

u0 = np.linspace(x_min, x_max, n_points)

v0 = (u0 - 1)**2 + 1

v = 2 * (u0 - 1)

u = np.sign(v)

v = np.abs(v)

fig, ax = plt.subplots()

ax.plot(x, y, color='royalblue', alpha=0.5)

ax.quiver(u0, v0, u, v)

ax.set_xlim(x_min, x_max)

ax.set_ylim(x_min, x_max)

ax.spines['top'].set_visible(False)

ax.spines['right'].set_visible(False)

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.set_aspect('equal')

plt.show()

2変数関数のgradient

勾配ベクトルの分布

2変数の関数について、gradientの分布を描いてみる。

関数として $z = x^2 + y^2$ を考えると、そのgradientは $( 2x, 2y)$ であり、ベクトル場は以下のようになる。

中心から外側に向かって増加しており、その傾きは外側ほど大きくなっている(ベクトルの長さが長くなり、コンター間隔は小さくなっている)。

import numpy as np
import matplotlib.pyplot as plt

lim_min = -1
lim_max = 1

x = np.linspace(lim_min, lim_max, 51)
y = np.linspace(lim_min, lim_max, 51)
x, y = np.meshgrid(x, y)
z = x * x + y* y

u0 = np.linspace(lim_min, lim_max, 21)
v0 = np.linspace(lim_min, lim_max, 21)
u0, v0 = np.meshgrid(u0, v0)
u = 2 * u0
v = 2 * v0

fig, ax = plt.subplots()

ax.contour(x, y, z)
ax.quiver(u0, v0, u, v)

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

lim_min = -1

lim_max = 1

x = np.linspace(lim_min, lim_max, 51)

y = np.linspace(lim_min, lim_max, 51)

x, y = np.meshgrid(x, y)

z = x * x + y* y

u0 = np.linspace(lim_min, lim_max, 21)

v0 = np.linspace(lim_min, lim_max, 21)

u0, v0 = np.meshgrid(u0, v0)

u = 2 * u0

v = 2 * v0

fig, ax = plt.subplots()

ax.contour(x, y, z)

ax.quiver(u0, v0, u, v)

ax.set_aspect('equal')

plt.show()

勾配ベクトルの曲面上での分布

微分係数の時と同じように、曲面上にgradientoの分布を描いてみたのが以下の図。

2次元の曲線の時と同じく、勾配ベクトルが曲面に沿った傾きを表していることがわかる。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

lim_min = -1
lim_max = 1
n_points=15

x = np.linspace(lim_min, lim_max, n_points)
y = np.linspace(lim_min, lim_max, n_points)
x, y = np.meshgrid(x, y)
z = x * x + y* y

u0 = x
v0 = y
w0 = u0 * u0 + v0 * v0
u = 2 * u0
v = 2 * v0
w = np.sqrt(u * u + v * v)
(u, v) = (u, v) / w

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.plot_wireframe(x, y, z, color='cyan')
ax.quiver(u0, v0, w0, u, v, w, length=0.2, normalize=True)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

lim_min = -1

lim_max = 1

n_points=15

x = np.linspace(lim_min, lim_max, n_points)

y = np.linspace(lim_min, lim_max, n_points)

x, y = np.meshgrid(x, y)

z = x * x + y* y

u0 = x

v0 = y

w0 = u0 * u0 + v0 * v0

u = 2 * u0

v = 2 * v0

w = np.sqrt(u * u + v * v)

(u, v) = (u, v) / w

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

ax.plot_wireframe(x, y, z, color='cyan')

ax.quiver(u0, v0, w0, u, v, w, length=0.2, normalize=True)

plt.show()

なお上記で(u, v) = (u, v) / wとしているが、 $\nabla f$ 方向で長さ1のベクトルを意味していて、これに対して $\nabla f$ をz方向の成分とすると曲面に沿ったベクトルとなる。

gradientの意味

2変数の場合

(4) $\begin{equation*} df(x, y) = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy = f_x dx + f_y dy \end{equation*}$

gradientの方向の意味

先の微分係数の考え方から、勾配の各成分は関数の各点においてその成分方向に増加する。

したがって、gradientの方向は、関数が増加する方向を指している。

gradientの大きさの意味

コーシー・シュワルツの不等式から、

(5) $\begin{equation*} | df(x, y) | ^2 = \left( f_x dx + f_y dy \right) ^2 \le ( f_x^2 + f_y^2 ) ( dx^2 + dy^2) \end{equation*}$

ここで右辺の最初の項がgradientの絶対値だから、

(6) $\begin{align*} | df(x, y) | ^2 \le | \nabla f |^2 ( dx^2 + dy^2) \end{align*}$

${\boldsymbol d} = (dx, dy)$ 、 $| {\boldsymbol d} | = C$ とすると、 $f(x, y)$ の ${\boldsymbol d}$ 方向の変化量の大きさは $C | \nabla f |$ 以下である。

また等号が成立するためには、

(7) $\begin{gather*} \left( f_x dx + f_y dy \right) ^2 - ( f_x^2 + f_y^2 ) ( dx^2 + dy^2) = 0 \\ 2 f_x dx f_y dy - f_x^2 dy^2 - f_y^2 dx^2 = 0 \\ (f_x dy - f_y dx)^2 = 0 \\ (f_x , f_y) \cdot (dy, -dx) = 0 \end{gather*}$

これは、 $\nabla f$ と $(dx, dy)$ の2つのベクトルが平行であることを意味している。

すなわちgradientの方向は、関数の変化量の大きさが最も大きくなる方向を指している。

gradientの意味

上記のことを併せると、gradientは以下のように最も勾配が大きな方向を意味することがわかる。

gradientの方向は、関数がその点で最も大きく増加する方向
gradientと逆の方向は、関数がその点で最も大きく減少する方向

n変数の場合

gradientの方向と大きさの意味は、2変数の場合と同じ。

不等式で等号が成立する場合を考える。

(8) $\begin{equation*} (f_{x_1} dx_1 + \cdots + f_{x_n} dx_n)^2 - (f_{x_1} ^2 + \cdots + f_{x_n} ^2) (dx_1 ^2 + \cdots + dx_n ^2) = 0 \end{equation*}$

左辺第1項は、

(9) $\begin{equation*} \begin{array}{cccccccc} f_{x_1} ^2 dx_1 ^2 &+& f_{x_1} dx_1 f_{x_2} dx_2 &+& \cdots &+& f_{x_1} dx_1 f_{x_n} dx_n &+\\ f_{x_2} dx_2 f_{x_1} dx_1 &+& f_{x_2} ^2 dx_2 ^2 &+& \cdots &+& f_{x_2} dx_2 f_{x_n} dx_n &+\\ &&&& \cdots &&& \\ f_{x_n} dx_n f_{x_1} dx_1 &+& f_{x_n} dx_n f_{x_1} dx_1 &+& \cdots &+& f_{x_n} ^2 dx_n ^2 \end{array} \end{equation*}$

また左辺第2項は、

(10) $\begin{equation*} \begin{array}{cccccccc} f_{x_1} ^2 dx_1 ^2 &+& f_{x_1} ^2 dx_2 ^2 &+& \cdots &+& f_{x_1} ^2 dx_n ^2 &+\\ f_{x_2} ^2 dx_1 ^2 &+& f_{x_2} ^2 dx_2 ^2 &+& \cdots &+& f_{x_2} ^2 dx_n ^2 &+\\&&&& \cdots &&& \\ f_{x_n} ^2 dx_1 ^2 &+& f_{x_n} ^2 dx_2 ^2 &+& \cdots &+& f_{x_n} ^2 dx_n ^2 &+\\\end{array} \end{equation*}$

それぞれ各項が行列でいえば対角になっていることに留意しながら、(10)から(9)を差し引いて以下を得る。

(11) $\begin{equation*} \sum_{i=1}^{n} \sum_{j=i}^{n} \left( f_{x_i} dx_j - f_{x_j} dx_i \right) ^2 = 0 \end{equation*}$

これは以下のようにも表せる。

(12) $\begin{equation*} f_{x_i} dx_j = f_{x_j} dx_i \quad (i \ne j) \end{equation*}$

これは以下を意味する。

(13) $\begin{equation*} f_{x_i} : dx_i = f_{x_j} : dx_j \quad (i \ne j) \end{equation*}$

すなわちn変数の場合でも、 $\nabla f$ と ${\boldsymbol d}$ の方向が一致するときに $f$ の変化量が最も大きい。

コーシー・シュワルツの不等式

2020-02-26 / tau / コメントする

公式

Cauchy-Schwaltz inequality

(1) $\begin{equation*} \left( \sum_{i=1}^n a_i ^2 \right) \left( \sum_{i=1}^n b_i ^2 \right) \ge \left( \sum_{i=1}^n a_i b_i \right) ^2 \end{equation*}$

証明

n=2の場合

(2) $\begin{equation*} \left( a_1^2 + a_2^2 \right) \left(b_1^2 + b_2^2 \right) \ge \left( a_1 b_1 + a_2 b_2 \right) ^2 \end{equation*}$

(3) $\begin{align*} &\left( a_1^2 + a_2^2 \right) \left(b_1^2 + b_2^2 \right) - \left( a_1 b_1 + a_2 b_2 \right) ^2 \\ &= a_1 ^2 b_1^2 + a_1^2 b_2^2 + a_2^2 b_1^2 + a_2^2 b_2^2 - a_1^2 b_1^2 - 2 a_1 b_1 a_2 b_2 - a_2^2 b_2^2 \\ &= a_1^2 b_2^2 + a_2^2 b_1^2 - 2 a_1 b_1 a_2 b_2 \\ &= \left( a_1 b_2 - a_2 b_1 \right) ^2 \ge 0 \end{align*}$

nが任意の場合

2次方程式の判別式による方法

以下の2次方程式を考える。

(4) $\begin{equation*} \sum_{i=1}^n \left( a_i x + b_i \right)^2 = 0 \end{equation*}$

ここで関数 $f(x) = \sum_{i=1}^2 (a_i x + b_i)^2 \ge 0$ であり、上記の2次方程式の数は0個または1個である。

この方程式は以下のように変形できる。

(5) $\begin{equation*} \left( \sum a_i^2 \right) x^2 + 2 \left( \sum a_i b_i \right) x + \left( \sum b_i^2 \right) = 0 \end{equation*}$

もとの方程式の解の個数が0 or 1なので、上記の方程式の判別式から

(6) $\begin{gather*} 4 \left( \sum a_i b_i \right)^2 - 4 \left( \sum a_i^2 \right) \left( \sum b_i^2 \right) \le 0 \\ \therefore \left( \sum a_i^2 \right) \left( \sum b_i^2 \right) \ge \left( \sum a_i b_i \right)^2 \end{gather*}$

イメージ

${\boldsymbol a} = (a_1, \ldots , a_n)$ 、 ${\boldsymbol b} = (b_1, \ldots , b_n)$ とすると、ベクトルの内積となす角の関係から

(7) $\begin{gather*} \left( {\boldsymbol a}{\boldsymbol b} \right)^2 = \left( \sum a_i b_i \right)^2 = | {\boldsymbol a} |^2 | {\boldsymbol b} |^2 \cos^2 \theta \le | {\boldsymbol a} |^2 | {\boldsymbol b} |^2 = \left( \sum a_i^2 \right) \left( \sum a_i^2 \right) \end{gather*}$

ラグランジュの未定乗数法～等式制約条件

2020-02-23 / tau / コメントする

準備

長方形の面積最大化

たとえば2変数の問題として、長方形の周囲長 $L$ を一定として、その面積が最大となる長方形の形状と面積はどのようになるかを考える。この場合、長方形の辺の長さを $x, y$ とすると、問題は以下のように表せる。

(1) $\begin{equation*} \mathrm{maximize} \quad S(x, y) = xy \quad \mathrm{subject~to} \quad x+y = \frac{L}{2} \end{equation*}$

これは以下のように代数的に簡単に解けて、答えは正方形とわかる。

(2) $\begin{gather*} S = x \left( \frac{L}{2} - x \right) = -x^2 + \frac{L}{2} x = - \left( x - \frac{L}{4} \right)^2 + \frac{L^2}{16} \\ \max S = \frac{L^2}{16} \quad \mathrm{for} \: x = y = \frac{L}{4} \end{gather*}$

ただし変数の数が増えたり、目的関数や制約条件が複雑になると、解析的に解くのが面倒になる。

Lgrangeの未定乗数法による解

解法から先に示す。Lagrangeの未定乗数法では、目的関数 $L(x, y)$ に対して以下の問題となる。

(3) $\begin{gather*} \mathrm{maximize} \quad L(x, y, \lambda) = S(x, y) - \lambda g(x, y) = xy - \lambda \left( x + y - \frac{L}{2} \right) \\ \mathrm{subject~to} \quad S(x, y) = xy, \quad g(x, y) = x + y - \frac{L}{2} \end{gather*}$

$L(x, y, \lambda)$ を最大化するために、 $x, y, \lambda$ で偏微分した以下の方程式を設定する。

(4) $\begin{gather*} \frac{\partial L}{\partial x} = 0, \quad \frac{\partial L}{\partial y} = 0, \quad \frac{\partial L}{\partial \lambda} = 0 \end{gather*}$

これを計算すると

(5) $\begin{gather*} y - \lambda = 0, \quad x - \lambda = 0, \quad x + y - \frac{L}{2}= 0 \\ \therefore \lambda = x = y = \frac{L}{4} \end{gather*}$

Lagrangeの未定乗数法の一般形

一般には、変数 $\boldsymbol{x} = (x_1, \ldots, x_n)$ について、目的関数 $f(\boldsymbol{x})$ を制約条件 $g(\boldsymbol{x})=0$ の下で最大化／最小化する問題として与えられる。

(6) $\begin{align*} & \mathrm{maximize/minimize} \quad f(\boldsymbol{x}) \\ & \mathrm{subject~to} \quad g(\boldsymbol{x}) = 0 \end{align*}$

この等式制約条件付き最大化／最小化問題は、以下のように $L(\boldsymbol{x}, \lambda)$ を導入して、連立方程式として表現される。

(7) $\begin{align*} & L(\boldsymbol{x}, \lambda) = f(\boldsymbol{x}) - \lambda g(\boldsymbol{x}) \\ & \frac{\partial L(\boldsymbol{x}, \lambda)}{\partial x_1} = \cdots = \frac{\partial L(\boldsymbol{x}, \lambda)}{\partial x_n} = \frac{\partial L(\boldsymbol{x}, \lambda)}{\partial \lambda} = 0 \end{align*}$

例題

例題1：平面と円

平面 $x + y - 1$ について、制約条件 $f(x, y) = x^2 + y^2$ の下での極値を求める。

(8) $\begin{align*} & \mathrm{minimize} \quad f(x, y) = x + y - 1 \\ & \mathrm{subject~to} \quad x^2 + y^2 = 1 \end{align*}$

lagrangeの未定乗数を導入して問題を定式化すると以下のようになる。

(9) $\begin{equation*} L(x, y, \lambda) = x + y - 1 - \lambda (x^2 + y^2 - 1) \end{equation*}$

(10) $\begin{align*} &\dfrac{\partial L}{\partial x} = 1 - 2 \lambda x = 0 \\ &\dfrac{\partial L}{\partial y} = 1 - 2 \lambda y = 0 \\ &\dfrac{\partial L}{\partial \lambda} = - x^2 - y^2 + 1 = 0 \end{align*}$

この連立方程式を解くと以下のようになり、解として2つの極値を得るが、それらは最大値と最小値に相当する。

(11) $\begin{gather*} x = y = \frac{1}{2 \lambda} \quad \Rightarrow \quad \frac{1}{4 \lambda ^2} + \frac{1}{4 \lambda ^2} = 1 \quad \Rightarrow \quad \lambda = \pm \frac{1}{\sqrt{2}}\\ \therefore \; x = y = \pm \frac{1}{\sqrt{2}} \approx \pm 0.7071\\ \max f(x, y) = \sqrt{2} - 1 \approx 0.414\\ \min f(x, y) = -\sqrt{2} - 1 \approx -2.414 \end{gather*}$

これを目的関数のコンターと制約条件の線で表すと以下の通り。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
x, y = np.meshgrid(x, y)

z = x + y - 1

fig = plt.figure()
ax = fig.add_subplot(111)

cntr = ax.contour(x, y, z ,levels=[-2.5, -2.414, -2, -1.5, -1, -0.5, 0, 0.414, 0.5])
ax.clabel(cntr)

crc = patches.Circle(xy=(0, 0), radius=1, fill=False)
ax.add_patch(crc)

s2 = 1 / np.sqrt(2)
ax.plot((0, s2), (s2, s2), c='k', linestyle='dotted')
ax.plot((s2, s2), (0, s2), c='k', linestyle='dotted')

ax.set_xlim((-1, 1))
ax.set_ylim((-1, 1))

ax.set_xticks([-1, -0.5, 0.5, 1])
ax.set_yticks([-1, -0.5, 0.5, 1])

ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)

ax.text(0.6, -0.08, "0.707", c='r')
ax.text(-0.23, 0.68, "0.707", c='r')

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as patches

x = np.linspace(-1, 1, 20)

y = np.linspace(-1, 1, 20)

x, y = np.meshgrid(x, y)

z = x + y - 1

fig = plt.figure()

ax = fig.add_subplot(111)

cntr = ax.contour(x, y, z ,levels=[-2.5, -2.414, -2, -1.5, -1, -0.5, 0, 0.414, 0.5])

ax.clabel(cntr)

crc = patches.Circle(xy=(0, 0), radius=1, fill=False)

ax.add_patch(crc)

s2 = 1 / np.sqrt(2)

ax.plot((0, s2), (s2, s2), c='k', linestyle='dotted')

ax.plot((s2, s2), (0, s2), c='k', linestyle='dotted')

ax.set_xlim((-1, 1))

ax.set_ylim((-1, 1))

ax.set_xticks([-1, -0.5, 0.5, 1])

ax.set_yticks([-1, -0.5, 0.5, 1])

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.spines['right'].set_visible(False)

ax.spines['top'].set_visible(False)

ax.text(0.6, -0.08, "0.707", c='r')

ax.text(-0.23, 0.68, "0.707", c='r')

ax.set_aspect('equal')

plt.show()

例題2：凸関数と直線

下に凸な関数 $f(x, y) = x^2 + y^2$ について、直線 $x + y = 1$ の制約条件下での最小値を求める。

(12) $\begin{align*} & \mathrm{minimize} \quad f(x, y) = x^2 + y^2 \\ & \mathrm {subject~to} \quad x + y - 1 = 0 \end{align*}$

ここでlagrangeの未定乗数を導入して問題を定式化すると以下のようになる。

(13) $\begin{equation*} L(x, y, \lambda) = x^2 + y^2 - \lambda (x + y - 1) \end{equation*}$

(14) $\begin{align*} &\dfrac{\partial L}{\partial x} = 2x - \lambda = 0 \\ &\dfrac{\partial L}{\partial y} = 2y - \lambda = 0 \\ &\dfrac{\partial L}{\partial \lambda} = - x - y + 1 = 0 \end{align*}$

この連立方程式を解くと以下のようになり、解は最小値1つとなる。

(15) $\begin{gather*} x = y = \frac{\lambda}{2} \quad \Rightarrow \quad \frac{\lambda}{2} + \frac{\lambda}{2} = 1 \quad \Rightarrow \quad \lambda = 1\\ \therefore \; x = y = \frac{1}{2} \quad , \quad \min f(x, y) = \frac{1}{2} \end{gather*}$

これを目的関数のコンターと制約条件の線で表すと以下の通り。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-1.5, 1.5, 40)
y = np.linspace(-1.5, 1.5, 40)
x, y = np.meshgrid(x, y)

z = x * x + y * y

fig = plt.figure()
ax = fig.add_subplot(111)

cntr = ax.contour(x, y, z, levels=[0.5, 1, 1.5, 2, 2.5])
ax.clabel(cntr)

ax.plot([-0.5, 1.5], [1.5, -0.5])

ax.plot((0, .5), (.5, .5), c='k', linestyle='dotted')
ax.plot((.5, .5), (0, .5), c='k', linestyle='dotted')

ax.set_xticks([-1, -0.5, 0.5, 1])
ax.set_yticks([-1, -0.5, 0.5, 1])

ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)

ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

x = np.linspace(-1.5, 1.5, 40)

y = np.linspace(-1.5, 1.5, 40)

x, y = np.meshgrid(x, y)

z = x * x + y * y

fig = plt.figure()

ax = fig.add_subplot(111)

cntr = ax.contour(x, y, z, levels=[0.5, 1, 1.5, 2, 2.5])

ax.clabel(cntr)

ax.plot([-0.5, 1.5], [1.5, -0.5])

ax.plot((0, .5), (.5, .5), c='k', linestyle='dotted')

ax.plot((.5, .5), (0, .5), c='k', linestyle='dotted')

ax.set_xticks([-1, -0.5, 0.5, 1])

ax.set_yticks([-1, -0.5, 0.5, 1])

ax.spines['bottom'].set_position('zero')

ax.spines['left'].set_position('zero')

ax.spines['right'].set_visible(False)

ax.spines['top'].set_visible(False)

ax.set_aspect('equal')

plt.show()

なお、これを3次元で表示すると以下のようになる。青い曲面が目的関数で、赤い直線が制約条件となる。最適化問題は、制約条件を満たす曲面上の点(図中、赤い放物線)の最小値を求めることになる。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

xmin, xmax = -2, 2
ymin, ymax = -2, 2
x = np.linspace(xmin, xmax)
y = np.linspace(ymin, ymax)

x_paraboloid, y_paraboloid = np.meshgrid(x, y)
z_paraboloid = x_paraboloid**2 + y_paraboloid**2

x_constraint = x.copy()
y_constraint = 1 - x
z_constraint = x_constraint**2 + y_constraint**2
for i, v in enumerate(y_constraint):
    if v <= ymin or v >= ymax:
        x_constraint[i] = np.nan
        y_constraint[i] = np.nan
        z_constraint[i] = np.nan

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(x_paraboloid, y_paraboloid, z_paraboloid, alpha=0.5)
ax.plot(x_constraint, y_constraint, z_constraint, color='r')
ax.plot(x_constraint, y_constraint, 0, color='r')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

xmin, xmax = -2, 2

ymin, ymax = -2, 2

x = np.linspace(xmin, xmax)

y = np.linspace(ymin, ymax)

x_paraboloid, y_paraboloid = np.meshgrid(x, y)

z_paraboloid = x_paraboloid**2 + y_paraboloid**2

x_constraint = x.copy()

y_constraint = 1 - x

z_constraint = x_constraint**2 + y_constraint**2

for i, v in enumerate(y_constraint):

if v <= ymin or v >= ymax:

x_constraint[i] = np.nan

y_constraint[i] = np.nan

z_constraint[i] = np.nan

fig = plt.figure()

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(x_paraboloid, y_paraboloid, z_paraboloid, alpha=0.5)

ax.plot(x_constraint, y_constraint, z_constraint, color='r')

ax.plot(x_constraint, y_constraint, 0, color='r')

plt.show()

幾何学的説明

式(7)は以下のように書ける。

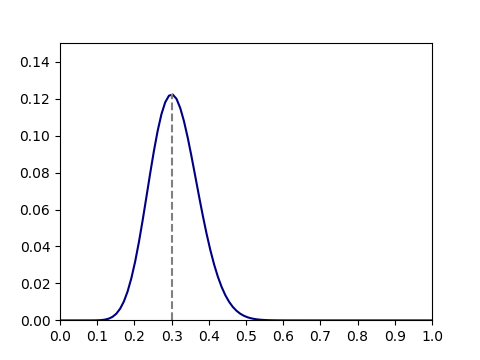
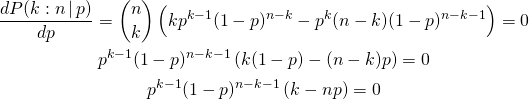
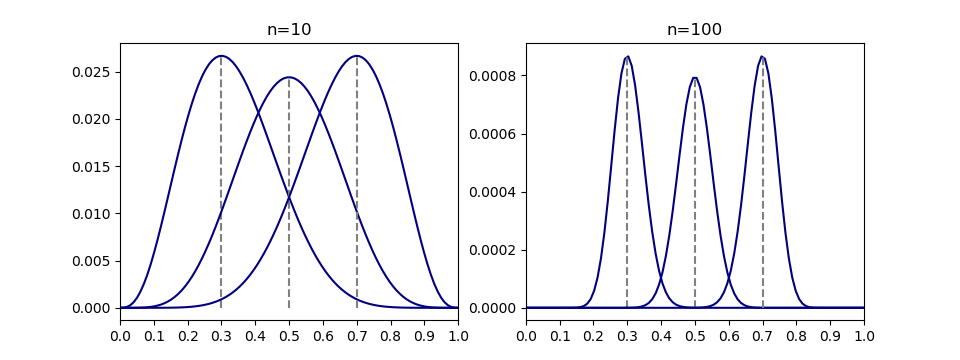
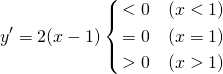
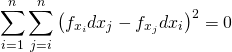
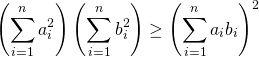
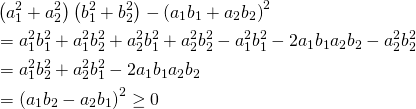
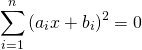
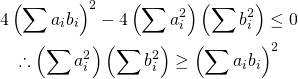
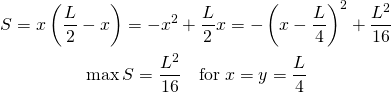
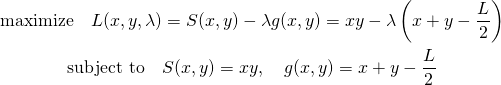
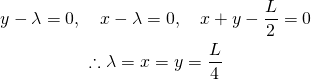
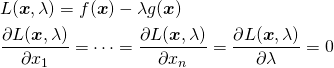
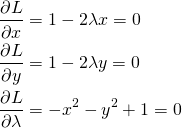
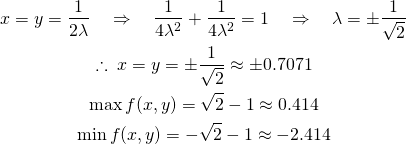
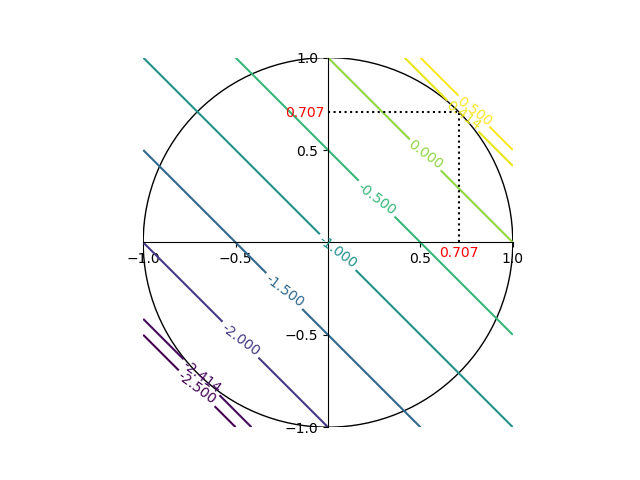
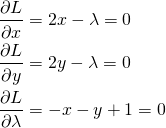
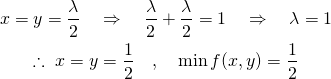
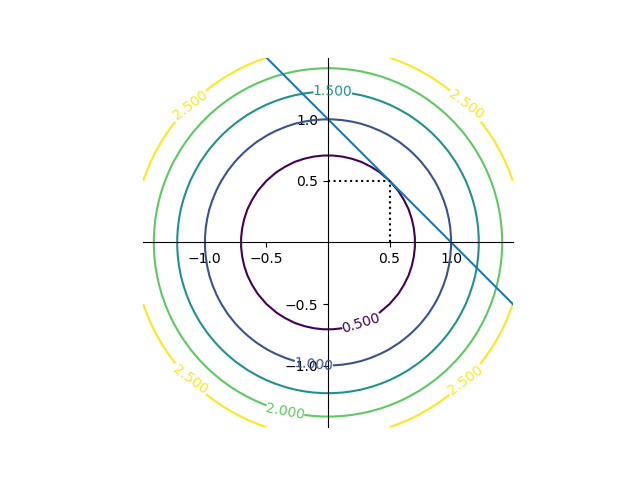
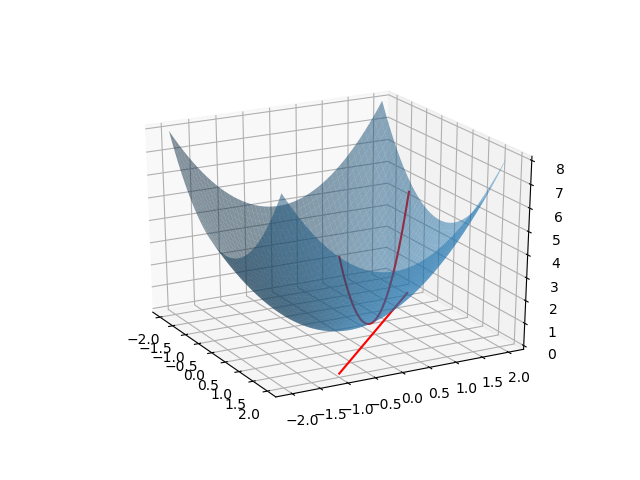
(16) $\begin{gather*} \left[ \begin{array}{c} \dfrac{\partial f}{\partial x_1} \\ \vdots \\ \dfrac{\partial f}{\partial x_n} \end{array} \right] = \lambda \left[ \begin{array}{c} \dfrac{\partial g}{\partial x_1} \\ \vdots \\ \dfrac{\partial g}{\partial x_n} \end{array} \right] \\ g(x_1, \ldots, x_n) = 0 \end{gather*}$

さらにgradientで表すと

(17) $\begin{gather*} \nabla f = \lambda \nabla g \\ g(x_1, \ldots, x_n) = 0 \end{gather*}$

すなわちこの式の解 $(x_1, \ldots, x_n)$ は、制約条件である $g(x_1, \ldots, x_n)=0$ を満足し、その曲線上にある。さらに解の点において $f(x_1, \ldots, x_n)$ の勾配ベクトルとゼロ平面上における $g(x_1, \ldots, x_n)$ の勾配ベクトルが平行になる。これはゼロ平面上の解の点において制約条件の曲線と $f(x_1, \ldots, x_n)$ のコンターのうち特定の曲線が接するのと同義であり、この点は停留点(stationary point)である。

つまりこのような停留点を発見する手順は、制約条件を満たす(制約条件の線上にある)点のうち、その点において目的関数のgradientと制約条件の関数のgradientが平行となる点を求めるということになる。再度これを式で表すと、

(18) $\begin{gather*} \nabla f(\boldsymbol{x}) = \lambda \nabla g(\boldsymbol{x}) \\ g(\boldsymbol{x}) = 0 \end{gather*}$

となるが、これをLangrange関数 $L=f - \lambda g$ と定義したうえで各変数で偏微分したものをゼロと置いた方程式を解くと表現している。未定乗数λは停留点における目的関数のgradientと制約条件の関数のgradientの比を表している。

λの符号

λの符号に意味があるかどうか。

たとえば、以下の制約条件付き最適化問題を考える。

(19) $\begin{align*} & \mathrm{minimize} \quad f(x, y) = x^2 + y^2 \\ & \mathrm {subject~to} \quad x + y - 2 = 0 \end{align*}$

(20) $\begin{gather*} L(x, y, \lambda) = x^2 + y^2 - \lambda(x + y - 2) \\ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} = \frac{\partial L}{\partial \lambda} = 0 \\ 2x - \lambda = 2y - \lambda = -x - y + 2 = 0\\ \lambda = 2, \; x=y=1 \end{gather*}$

この問題の制約条件を変更して以下のようにした場合。

(21) $\begin{align*} & \mathrm{minimize} \quad f(x, y) = x^2 + y^2 \\ & \mathrm {subject~to} \quad - x - y + 2 = 0 \end{align*}$

(22) $\begin{gather*} L(x, y, \lambda) = x^2 + y^2 - \lambda(- x - y + 2) \\ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} = \frac{\partial L}{\partial \lambda} = 0 \\ 2x + \lambda = 2y + \lambda = x + y - 2 = 0\\ \lambda = -2, \; x=y=1 \end{gather*}$

このように、制約条件の正負を反転するとλの符号が逆になるが解は変わらない。これを表したのが以下の図。

等式制約条件の場合、制約条件の線上でgradientが平行になりさえすればよいので、λ符号(制約条件式の正負)には拘らなくてよい。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patch
from mpl_toolkits.mplot3d import Axes3D

xmin, xmax = -3, 3
ymin, ymax = -3, 3
xls, xle = -1, 3
yls, yle = 3, -1

xs = np.linspace(xmin, xmax)
ys = np.linspace(ymin, ymax)
xm, ym = np.meshgrid(xs, ys)

zero_plain = np.full_like(xm, 0)
z_prb = xm**2 + ym**2
z_pl1 = xm + ym - 2
z_pl2 = - xm - ym + 2

r = np.sqrt(2)
t = np.linspace(-np.pi, np.pi, num=100)
xc = r * np.cos(t)
yc = r * np.sin(t)
uqc = 2 * xc
vqc = 2 * yc

xql = np.linspace(xls, xle, num=80)
yql = np.linspace(yls, yle, num=80)
uql1 = np.full_like(xql, 1)
vql1 = np.full_like(yql, 1)
uql2 = np.full_like(xql, -1)
vql2 = np.full_like(yql, -1)

fig = plt.figure(figsize=(11, 4.8))
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122)

ax1.plot_surface(xm, ym, zero_plain, color='gray', alpha=0.5)
ax1.plot_surface(xm, ym, z_prb, color='tab:blue', alpha=0.5)
ax1.plot_surface(xm, ym, z_pl1, color='tab:orange', alpha=0.5)
ax1.plot_surface(xm, ym, z_pl2, color='tab:green', alpha=0.5)
ax1.plot([xls, yls], [xle, yle], [0, 0], c='k')
ax1.set_xlabel("x")
ax1.set_ylabel("y")

ax2.plot(xc, yc, c='b')
ax2.plot([xls, yls], [xle, yle], c='k')
ax2.quiver(xc, yc, uqc, vqc, scale_units='xy', scale=4, color='tab:blue', alpha=0.5)
ax2.quiver(xql, yql, uql1, vql1, scale_units='xy', scale=4, color='tab:orange', alpha=0.5)
ax2.quiver(xql, yql, uql2, vql2, scale_units='xy', scale=4, color='tab:green', alpha=0.5)
ax2.set_xlabel("x")
ax2.set_ylabel("y")

ax2.set_xlim(0, 2)
ax2.set_ylim(0, 2)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as patch

from mpl_toolkits.mplot3d import Axes3D

xmin, xmax = -3, 3

ymin, ymax = -3, 3

xls, xle = -1, 3

yls, yle = 3, -1

xs = np.linspace(xmin, xmax)

ys = np.linspace(ymin, ymax)

xm, ym = np.meshgrid(xs, ys)

zero_plain = np.full_like(xm, 0)

z_prb = xm**2 + ym**2

z_pl1 = xm + ym - 2

z_pl2 = - xm - ym + 2

r = np.sqrt(2)

t = np.linspace(-np.pi, np.pi, num=100)

xc = r * np.cos(t)

yc = r * np.sin(t)

uqc = 2 * xc

vqc = 2 * yc

xql = np.linspace(xls, xle, num=80)

yql = np.linspace(yls, yle, num=80)

uql1 = np.full_like(xql, 1)

vql1 = np.full_like(yql, 1)

uql2 = np.full_like(xql, -1)

vql2 = np.full_like(yql, -1)

fig = plt.figure(figsize=(11, 4.8))

ax1 = fig.add_subplot(121, projection='3d')

ax2 = fig.add_subplot(122)

ax1.plot_surface(xm, ym, zero_plain, color='gray', alpha=0.5)

ax1.plot_surface(xm, ym, z_prb, color='tab:blue', alpha=0.5)

ax1.plot_surface(xm, ym, z_pl1, color='tab:orange', alpha=0.5)

ax1.plot_surface(xm, ym, z_pl2, color='tab:green', alpha=0.5)

ax1.plot([xls, yls], [xle, yle], [0, 0], c='k')

ax1.set_xlabel("x")

ax1.set_ylabel("y")

ax2.plot(xc, yc, c='b')

ax2.plot([xls, yls], [xle, yle], c='k')

ax2.quiver(xc, yc, uqc, vqc, scale_units='xy', scale=4, color='tab:blue', alpha=0.5)

ax2.quiver(xql, yql, uql1, vql1, scale_units='xy', scale=4, color='tab:orange', alpha=0.5)

ax2.quiver(xql, yql, uql2, vql2, scale_units='xy', scale=4, color='tab:green', alpha=0.5)

ax2.set_xlabel("x")

ax2.set_ylabel("y")

ax2.set_xlim(0, 2)

ax2.set_ylim(0, 2)

plt.show()

停留点が極致とならない例

以下の最適化問題の解をみてみる。

(23) $\begin{align*} & \mathrm{maxmize} \quad f(x, y) = x^3 + y^3 \\ & \mathrm{subject~to} \quad g(x, y) = x - y \end{align*}$

(24) $\begin{align*} &L(x, y, \lambda) = x^3 + y^3 - \lambda(x - y) \\ &\left\{ \begin{array}{c} \dfrac{\partial L}{\partial x} = 3x^2 - \lambda = 0\\ \\ \dfrac{\partial L}{\partial y} = 3y^2 + \lambda= 0\\ \\ \dfrac{\partial L}{\partial \lambda} = x - y = 0 \end{array} \right. \end{align*}$

第1式から第2式を引き、第3式を適用して、

(25) $\begin{gather*} \3x^2 - 3y^2 - 2\lambda = 0 \\ 3(x + y)(x - y) = 2\lambda = 0 \\ \therefore x = y = \lambda = 0 \end{gather*}$

ここで $z=f(x, y)$ の曲面と制約条件 $g(x, y)=0$ に対する曲面上の軌跡を描くと下図左のようになる。下図の右は $t = x = y$ として曲線を表したもので、 $x = y = 0$ で勾配は水平になっており、停留点ではあるが極大／極小となっていない。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x = np.linspace(-1, 1)
y = np.linspace(-1, 1)
xs, ys = np.meshgrid(x, y)
zs = xs**3 + ys**3

t = np.linspace(-1, 1)
xp = yp = t
zp = xp**3 + yp**3

fig = plt.figure(figsize=(13, 4.8))
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122)

ax1.plot_surface(xs, ys, zs, alpha=0.5)
ax1.plot(xp, yp, zp)
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.set_xticks(np.arange(-1, 1.5, 0.5))
ax1.set_yticks(np.arange(-1, 1.5, 0.5))

ax2.plot(t, zp)
ax2.plot((-2, 2), (0, 0), c='k')
ax2.plot((0, 0), (-2, 2), c='k')
ax2.set_xlim(-2, 2)
ax2.set_ylim(-2, 2)
ax2.spines['top'].set_visible(False)
ax2.spines['right'].set_visible(False)
ax2.set_xlabel("t")
ax2.set_ylabel("z")
ax2.set_aspect('equal')
ax2.grid(True)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

x = np.linspace(-1, 1)

y = np.linspace(-1, 1)

xs, ys = np.meshgrid(x, y)

zs = xs**3 + ys**3

t = np.linspace(-1, 1)

xp = yp = t

zp = xp**3 + yp**3

fig = plt.figure(figsize=(13, 4.8))

ax1 = fig.add_subplot(121, projection='3d')

ax2 = fig.add_subplot(122)

ax1.plot_surface(xs, ys, zs, alpha=0.5)

ax1.plot(xp, yp, zp)

ax1.set_xlabel("x")

ax1.set_ylabel("y")

ax1.set_xticks(np.arange(-1, 1.5, 0.5))

ax1.set_yticks(np.arange(-1, 1.5, 0.5))

ax2.plot(t, zp)

ax2.plot((-2, 2), (0, 0), c='k')

ax2.plot((0, 0), (-2, 2), c='k')

ax2.set_xlim(-2, 2)

ax2.set_ylim(-2, 2)

ax2.spines['top'].set_visible(False)

ax2.spines['right'].set_visible(False)

ax2.set_xlabel("t")

ax2.set_ylabel("z")

ax2.set_aspect('equal')

ax2.grid(True)

plt.show()

参考サイト

本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。

その２極値を求めるラグランジュの未定乗数法～○×（まるぺけ）つくろーどっとコム

matplotlib.pyplot.quiver – ベクトル場

2020-02-23 / tau / 3件のコメント

概要

matplotlib.pyplot.quiver()はベクトル場を可視化する。基本的なパラメーターは以下の通り。

quiver(X, Y, U, V, [C]): X, Yはベクトルの開始点、U, Vはベクトルの成分、Cはベクトルの大きさに応じたカラーマップ上の色をつけるための配列。

単一のベクトルの描画例

以下の例では、始点の位置と成分を1つずつ指定してベクトルを描画している。デフォルトではベクトルのスケールは描画領域に対して自動的に調節されるが、ここでは描画領域のスケールと同じになるようパラメーターを設定している。

matplotlibのドキュメントでは、scale_unitsのところに以下のように書かれている。

“To plot vectors in the x-y plane, with u and v having the same units as x and y, use angles='xy', scale_units='xy', scale=1”

import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.quiver(1, 2, color='blue', angles='xy', scale_units='xy', scale=1)
ax.quiver(1, 2, 2, -1, color='red', angles='xy', scale_units='xy', scale=1)

ax.set_xlim(0, 3)
ax.set_ylim(0, 3)

ax.set_xticks(np.arange(0, 4, 1))
ax.set_yticks(np.arange(0, 4, 1))

ax.grid()
ax.set_aspect('equal')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.quiver(1, 2, color='blue', angles='xy', scale_units='xy', scale=1)

ax.quiver(1, 2, 2, -1, color='red', angles='xy', scale_units='xy', scale=1)

ax.set_xlim(0, 3)

ax.set_ylim(0, 3)

ax.set_xticks(np.arange(0, 4, 1))

ax.set_yticks(np.arange(0, 4, 1))

ax.grid()

ax.set_aspect('equal')

plt.show()

ベクトル場の描画例

以下の例では、xy平面上の位置に応じた成分を持つベクトルを描画している。関数のgradientのイメージ。

描画にあたって、開始点の座標とベクトルの成分をmeshgridで生成している。

1つ目の図は単に開始点と成分を与えただけで、単一の色で、ベクトルのスケールは自動調節されている。

2つ目の図はスケールと色付けのための配列を指定し、ベクトルの大きさに応じてcolormapで色を付けている。

import numpy as np
import matplotlib.pyplot as plt

x = y = np.arange(-5, 6)
u = 2 * x
v = 3 * y

x, y = np.meshgrid(x, y)
u, v = np.meshgrid(u, v)

fig, axes = plt.subplots(1, 2, figsize=(12, 4.8))

lim = 8
for ax in axes:
    ax.set_xlim(-lim, lim)
    ax.set_ylim(-lim, lim)

    ax.set_xticks(np.arange(-lim, lim, 1))
    ax.set_yticks(np.arange(-lim, lim, 1))

    ax.grid()
    ax.set_aspect('equal')

C = np.sqrt(u * u + v * v)
axes[0].quiver(x, y, u, v)
axes[1].quiver(x, y, u, v, C, scale=100, cmap='Blues')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

x = y = np.arange(-5, 6)

u = 2 * x

v = 3 * y

x, y = np.meshgrid(x, y)

u, v = np.meshgrid(u, v)

fig, axes = plt.subplots(1, 2, figsize=(12, 4.8))

lim = 8

for ax in axes:

ax.set_xlim(-lim, lim)

ax.set_ylim(-lim, lim)

ax.set_xticks(np.arange(-lim, lim, 1))

ax.set_yticks(np.arange(-lim, lim, 1))

ax.grid()

ax.set_aspect('equal')

C = np.sqrt(u * u + v * v)

axes[0].quiver(x, y, u, v)

axes[1].quiver(x, y, u, v, C, scale=100, cmap='Blues')

plt.show()

概要

データの取得とデータ構造

データの内容

'data'～特徴量データセット

'target'～アヤメの種類に対応したコード

'target_names'～アヤメの種類名

'feature_names'～特徴名

'filename'～ファイル名

'DESCR'～データセットの説明

データの利用

データの取得方法

全レコードの特徴量データの取得

特定の特徴量のデータのみ取得

特定のクラスのデータのみ抽出

概要

ヒストグラムの形式

度数分布

頻度分布

累積分布図

ビン数

レンジ

色・エッジの指定

ビンの幅

ヒストグラムのタイプ

複数のヒストグラム

単純な重ね合わせ

ヒストグラムとplotの重ね合わせ

ビン境界の整合

並べる・積み上げる

戻り値

単一のヒストグラムの場合

複数のヒストグラムの配列の場合

概要

確率分布

全事象

平均と分散

二項分布の形

正規分布近似

母集団確率の最尤推定

実用例

適用例

分析例

コインの例

尤度関数と最尤法

サンプルの質と尤度

リスト要素の重複を除く

ndarrayの要素の重複を除く

利用例～クラス値を持つデータの分類

定義

準備～1変数関数の微分係数

微分係数の符号だけを見た場合

微分係数の符号を方向としてみた場合

微分係数の曲線上での分布

2変数関数のgradient

勾配ベクトルの分布

勾配ベクトルの曲面上での分布

gradientの意味

2変数の場合

gradientの方向の意味

gradientの大きさの意味

gradientの意味

n変数の場合

公式

証明

n=2の場合

nが任意の場合

2次方程式の判別式による方法

イメージ

準備

長方形の面積最大化

Lgrangeの未定乗数法による解

Lagrangeの未定乗数法の一般形

例題

例題1：平面と円

例題2：凸関数と直線

幾何学的説明

λの符号

停留点が極致とならない例

参考サイト

概要

`'data'`～特徴量データセット

`'target'`～アヤメの種類に対応したコード

`'target_names'`～アヤメの種類名

`'feature_names'`～特徴名

`'filename'`～ファイル名

`'DESCR'`～データセットの説明