scikit-learn – make_blobs

2020-05-18 / tau / コメントする

概要

sklearn.datasets.make_blobls()は、クラス分類のためのデータを生成する。blobとはインクの染みなどを指し、散布図の点の様子からつけられてるようだ。

標準では、データの総数、特徴量の数、クラスターの数などを指定して実行し、特徴量配列X、ターゲットとなるクラスデータyのタプルが返される（引数の指定によってはもう1つ戻り値が追加される）。

得られるデータの形式

特徴量配列Xは列が特徴量、行がレコードの2次元配列。ターゲットyはレコード数分のクラス属性値の整数。

from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=10, random_state=0)

print(X)
print(y)

# [[ 1.12031365  5.75806083]
#  [ 1.7373078   4.42546234]
#  [ 2.36833522  0.04356792]
#  [ 0.87305123  4.71438583]
#  [-0.66246781  2.17571724]
#  [ 0.74285061  1.46351659]
#  [-4.07989383  3.57150086]
#  [ 3.54934659  0.6925054 ]
#  [ 2.49913075  1.23133799]
#  [ 1.9263585   4.15243012]]
# [0 0 1 0 2 2 2 1 1 0]

from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=10, random_state=0)

print(X)

print(y)

# [[ 1.12031365 5.75806083]

# [ 1.7373078 4.42546234]

# [ 2.36833522 0.04356792]

# [ 0.87305123 4.71438583]

# [-0.66246781 2.17571724]

# [ 0.74285061 1.46351659]

# [-4.07989383 3.57150086]

# [ 3.54934659 0.6925054 ]

# [ 2.49913075 1.23133799]

# [ 1.9263585 4.15243012]]

# [0 0 1 0 2 2 2 1 1 0]

利用例

そのままscikit-learnのモデルの入力とする。

from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

X, y = make_blobs(n_samples=100, centers=2, random_state=0)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

clf = KNeighborsClassifier(n_neighbors=1)
clf.fit(X_train, y_train)

print(clf.score(X_train, y_train))
print(clf.score(X_test, y_test))
# 1.0
# 0.96

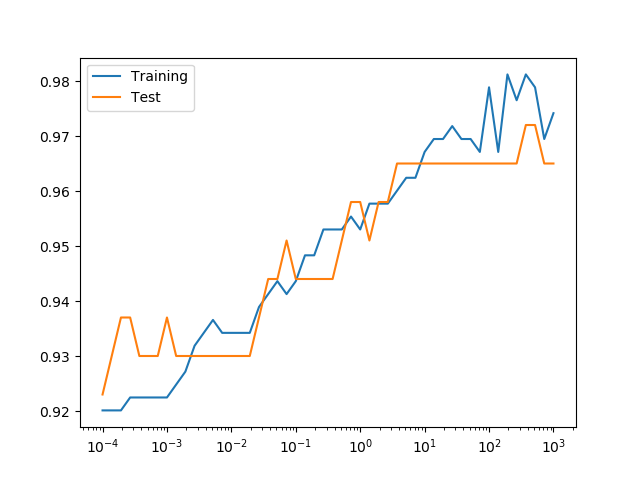
from sklearn.datasets import make_blobs

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsClassifier

X, y = make_blobs(n_samples=100, centers=2, random_state=0)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

clf = KNeighborsClassifier(n_neighbors=1)

clf.fit(X_train, y_train)

print(clf.score(X_train, y_train))

print(clf.score(X_test, y_test))

# 1.0

# 0.96

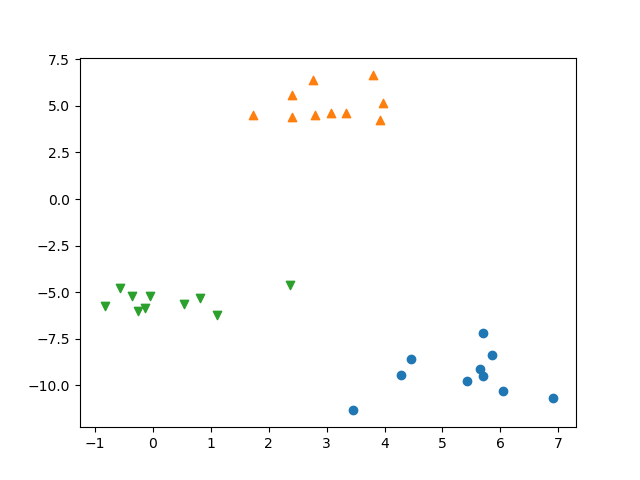
クラスごとに色やマークを変えて散布図を描く。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=30, centers=3, random_state=10)

markers = ['o', '^', 'v']
fig, ax = plt.subplots()

for cluster, marker in zip(range(3), markers):
    x = X[y==cluster]
    ax.scatter(x[:, 0], x[:, 1], marker=marker)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=30, centers=3, random_state=10)

markers = ['o', '^', 'v']

fig, ax = plt.subplots()

for cluster, marker in zip(range(3), markers):

x = X[y==cluster]

ax.scatter(x[:, 0], x[:, 1], marker=marker)

plt.show()

パラメーターの指定

make_blobs(n_samples, n_features, centers, cluster_std,
           center_box, shuffle, random_state, return_centers)

1 2	make_blobs(n_samples, n_features, centers, cluster_std, center_box, shuffle, random_state, return_centers)

主なもの。

n_samples: 整数で指定した場合、生成されるサンプルの総数で戻り値Xの行数になる。配列で指定した場合、その要素数がクラスターの数となり、各要素はクラスターのデータ数となる。デフォルトは100。
n_features: 特徴量の数で、戻り値Xの列数になる。デフォルトは2
centers: クラスター中心の数。n_samplesを整数で指定してcentersを指定しない場合（デフォルトのNoneの場合）、centers=3となる。n_samplesを配列で指定した場合はNoneか[n_centers, n_features]の配列。
center_std: クラスターの標準偏差。

Logistic回帰～cancer～Pythonではじめる機械学習より

2020-05-17 / tau / コメントする

モデルの精度

breast_cancerデータセットに対してLogistic回帰モデル、scikit-learnのLogisticRegression適用し、訓練データとテストデータのスコアを計算してみる。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression().fit(X_train, y_train)
print("")
print("Training score: {}".format(logreg.score(X_train, y_train)))
print("Test score    : {}".format(logreg.score(X_test, y_test)))

# Training score: 0.9530516431924883
# Test score    : 0.958041958041958

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression().fit(X_train, y_train)

print("")

print("Training score: {}".format(logreg.score(X_train, y_train)))

print("Test score : {}".format(logreg.score(X_test, y_test)))

# Training score: 0.9530516431924883

# Test score : 0.958041958041958

（注）solverに関する警告と計算結果

上のコードを実行したとき、結果は書籍と整合しているが、警告表示が出た

...FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.
  FutureWarning)
Training score: 0.9530516431924883
Test score    : 0.958041958041958

...FutureWarning: Default solver will be changed to 'lbfgs' in 0.22. Specify a solver to silence this warning.

FutureWarning)

Training score: 0.9530516431924883

Test score : 0.958041958041958

この時点でscikit-learnのバージョンが古く(0.21.3)、将来のデフォルトが変更されるとのこと。そこでインスタンス生成時にデフォルトのソルバーを明示的にsolver='liblinear'と指定して実行すると、警告は出ず値もそのまま。

なお、solver='lbfgs'としてみたところ、計算が収束しない旨の警告が出た。

logreg = LogisticRegression(solver='lbfgs').fit(X_train, y_train)

1	logreg = LogisticRegression(solver='lbfgs').fit(X_train, y_train)

...ConvergenceWarning: lbfgs failed to converge. Increase the number of iterations.
  "of iterations.", ConvergenceWarning)
Training score: 0.9483568075117371
Test score    : 0.951048951048951

...ConvergenceWarning: lbfgs failed to converge. Increase the number of iterations.

"of iterations.", ConvergenceWarning)

Training score: 0.9483568075117371

Test score : 0.951048951048951

そこで収束回数を増やしていったところ、最大回数2000では収束せず、3000で収束し、警告は出なくなった。

logreg = LogisticRegression(solver='lbfgs', max_iter=3000).fit(X_train, y_train)

1	logreg = LogisticRegression(solver='lbfgs', max_iter=3000).fit(X_train, y_train)

Training score: 0.9577464788732394
Test score    : 0.958041958041958

1 2	Training score: 0.9577464788732394 Test score : 0.958041958041958

その後、scikit-learnのバージョンを0.23.0にアップグレードしたところ、デフォルトで警告は表示されず、収束回数に関する警告が同じように出て、結果も再現された。以下、ソルバーとしてliblinearを明示的に指定し、random_stateの値も書籍と同じ値として確認する。

学習精度の向上

先のC=1.0とliblinearによるスコアは、訓練データに対して0.953、テストデータに対して0.958と両方に対して高い値となっている。ここで、訓練データとテストデータのスコアが近いということは、適合不足の可能性がある。そこでC=100と値を大きくして、より柔軟なモデルにしてみる（柔軟なモデルとは、正則化を弱めて訓練データによりフィットしやすくしたモデル）。

logreg100 = LogisticRegression(C=100, solver='liblinear').fit(X_train, y_train)
print("Training score: {}".format(logreg100.score(X_train, y_train)))
print("Test score    : {}".format(logreg100.score(X_test, y_test)))

# Training score: 0.9788732394366197
# Test score    : 0.965034965034965

logreg100 = LogisticRegression(C=100, solver='liblinear').fit(X_train, y_train)

print("Training score: {}".format(logreg100.score(X_train, y_train)))

print("Test score : {}".format(logreg100.score(X_test, y_test)))

# Training score: 0.9788732394366197

# Test score : 0.965034965034965

訓練データ、テストデータともそれぞれ若干向上している。なお、Cの値を1000、10000ともっと大きくしてもスコアはほとんど変わらない。

今度は逆に、Cの値を1.0より小さくして正則化を強めてみると、訓練データ、テストデータ両方に対するスコアが下がってしまう。

logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)
print("Training score: {}".format(logreg001.score(X_train, y_train)))
print("Test score    : {}".format(logreg001.score(X_test, y_test)))

# Training score: 0.9342723004694836
# Test score    : 0.9300699300699301

logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)

print("Training score: {}".format(logreg001.score(X_train, y_train)))

print("Test score : {}".format(logreg001.score(X_test, y_test)))

# Training score: 0.9342723004694836

# Test score : 0.9300699300699301

Cを変化させたときの学習率曲線は以下の通り。Cが10より小さいところでは正則化が強く学習不足、そこを超えると学習率が頭打ちで、学習率の改善はそれほど顕著ではない。Logistic回帰モデルの学習率曲線のバリエーションについては、こちらでまとめている。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

C_pow_min = -4
C_pow_max = 3
C_pow_num = 100
Cs_pows = np.linspace(C_pow_min, C_pow_max, C_pow_num)
Cs = 10**Cs_pows

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

fig, ax = plt.subplots()

score_trains = np.empty(0)
score_tests = np.empty(0)

for C in Cs:
    logreg = LogisticRegression(C=C, solver='liblinear').fit(X_train, y_train)
    score_trains = np.append(score_trains, logreg.score(X_train, y_train))
    score_tests = np.append(score_tests, logreg.score(X_test, y_test))

ax.plot(Cs, score_trains, label="Training")
ax.plot(Cs, score_tests, label="Test")

ax.set_xscale('log')
ax.legend()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

C_pow_min = -4

C_pow_max = 3

C_pow_num = 100

Cs_pows = np.linspace(C_pow_min, C_pow_max, C_pow_num)

Cs = 10**Cs_pows

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

fig, ax = plt.subplots()

score_trains = np.empty(0)

score_tests = np.empty(0)

for C in Cs:

logreg = LogisticRegression(C=C, solver='liblinear').fit(X_train, y_train)

score_trains = np.append(score_trains, logreg.score(X_train, y_train))

score_tests = np.append(score_tests, logreg.score(X_test, y_test))

ax.plot(Cs, score_trains, label="Training")

ax.plot(Cs, score_tests, label="Test")

ax.set_xscale('log')

ax.legend()

plt.show()

特徴量の係数

L2正則化の場合

breast_cancerデータセットに対してLogisticRegressionを学習させた場合の、30個の特徴量に対する係数をプロットする。liblinearソルバーで、デフォルトでL2正則化を行っている。Cの値が大きいほど正則化の効果が弱く、係数の絶対値が大きくなっている。

書籍で注意喚起しているのは3番目の特徴量mean perimeterで、モデルによって正負が入れ替わることから、クラス分類に対する信頼性を問題にしている。

ここで書籍について以下の点が気になった。

logreg001のインスタンス生成時にC=0.01としているが、凡例で”C=0.001″としている（グラフの結果はあまり変わらない）
logreg100でC=100とすると、書籍にあるような結果にならない（worst concave pointsが-8以下になるなど、分布が大幅に変わってくる）
C=20とすると、概ね書籍と同じ分布になる（若干異なる部分は残る）

いずれにしても”Pythonではじめる機械学習”は、入門者にとってとてもありがたいきっかけを提供してくれる良著であることに変わりはない。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as pch
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

logreg1 = LogisticRegression(solver='liblinear').fit(X_train, y_train)
logreg20 = LogisticRegression(C=20, solver='liblinear').fit(X_train, y_train)
logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)

x_scatter = np.linspace(0, 1, len(ds.feature_names))

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(x_scatter, logreg1.coef_, marker='o', c='grey', s=100,
    label="C=1.0")
ax.scatter(x_scatter, logreg001.coef_, marker='1', c='blue', s=100,
    label="C=0.01")
ax.scatter(x_scatter, logreg20.coef_, marker='2', c='red', s = 100,
    label="C=20")
ax.plot([0, 1], [0, 0], c='k', zorder=-100)
ax.add_patch(pch.Arrow(2/30, -4, 0, 3, width=1/30))

ax.set_xticks(x_scatter)
ax.set_xticklabels(ds.feature_names, rotation=90)
ax.set_xlim(0, 1)
ax.legend()

fig.subplots_adjust(bottom=0.3)

plt.show()

import numpy as np

import matplotlib.pyplot as plt

import matplotlib.patches as pch

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

logreg1 = LogisticRegression(solver='liblinear').fit(X_train, y_train)

logreg20 = LogisticRegression(C=20, solver='liblinear').fit(X_train, y_train)

logreg001 = LogisticRegression(C=0.01, solver='liblinear').fit(X_train, y_train)

x_scatter = np.linspace(0, 1, len(ds.feature_names))

fig, ax = plt.subplots(figsize=(6.4, 6.4))

ax.scatter(x_scatter, logreg1.coef_, marker='o', c='grey', s=100,

label="C=1.0")

ax.scatter(x_scatter, logreg001.coef_, marker='1', c='blue', s=100,

label="C=0.01")

ax.scatter(x_scatter, logreg20.coef_, marker='2', c='red', s = 100,

label="C=20")

ax.plot([0, 1], [0, 0], c='k', zorder=-100)

ax.add_patch(pch.Arrow(2/30, -4, 0, 3, width=1/30))

ax.set_xticks(x_scatter)

ax.set_xticklabels(ds.feature_names, rotation=90)

ax.set_xlim(0, 1)

ax.legend()

fig.subplots_adjust(bottom=0.3)

plt.show()

L1正則化の場合

ソルバーを同じliblinearとして、penalty='l1'と明示的に指定する。今回はL2正則化の時と違って、C=0.001はコード中に明示され、C=100としてスコアの計算結果まで合う。ただしset_ylim()によって表示範囲を制限しており、C=100に対するいくつかの点が枠外にある。

L1正則化によって、多くの係数がゼロとなり、少ない特徴量によるシンプルなモデルでそれなりのスコアを出している。

logreg1 = LogisticRegression(solver='liblinear', penalty='l1').\
    fit(X_train, y_train)
logreg100 = LogisticRegression(C=100, solver='liblinear', penalty='l1').\
    fit(X_train, y_train)
logreg001 = LogisticRegression(C=0.001, solver='liblinear', penalty='l1').\
    fit(X_train, y_train)
print("C=0.001")
print(" Training score: {:5.3f}".format(logreg001.score(X_train, y_train)))
print(" Test score    : {:5.3f}".format(logreg001.score(X_test, y_test)))
print("C=1")
print(" Training score: {:5.3f}".format(logreg1.score(X_train, y_train)))
print(" Test score    : {:5.3f}".format(logreg1.score(X_test, y_test)))
print("C=100")
print(" Training score: {:5.3f}".format(logreg100.score(X_train, y_train)))
print(" Test score    : {:5.3f}".format(logreg100.score(X_test, y_test)))

# C=0.001
#  Training score: 0.913
#  Test score    : 0.923
# C=1
#  Training score: 0.960
#  Test score    : 0.958
# C=100
#  Training score: 0.986
#  Test score    : 0.979

logreg1 = LogisticRegression(solver='liblinear', penalty='l1').\

fit(X_train, y_train)

logreg100 = LogisticRegression(C=100, solver='liblinear', penalty='l1').\

fit(X_train, y_train)

logreg001 = LogisticRegression(C=0.001, solver='liblinear', penalty='l1').\

fit(X_train, y_train)

print("C=0.001")

print(" Training score: {:5.3f}".format(logreg001.score(X_train, y_train)))

print(" Test score : {:5.3f}".format(logreg001.score(X_test, y_test)))

print("C=1")

print(" Training score: {:5.3f}".format(logreg1.score(X_train, y_train)))

print(" Test score : {:5.3f}".format(logreg1.score(X_test, y_test)))

print("C=100")

print(" Training score: {:5.3f}".format(logreg100.score(X_train, y_train)))

print(" Test score : {:5.3f}".format(logreg100.score(X_test, y_test)))

# C=0.001

# Training score: 0.913

# Test score : 0.923

# C=1

# Training score: 0.960

# Test score : 0.958

# C=100

# Training score: 0.986

# Test score : 0.979

係数の符号と選択確率について

ターゲットのクラスは、malignant(悪性)が0、benign(良性)が1で、係数が正の場合は良性となる確率を上げる方向に、負の場合は悪性となる確率を上げる方向に効くことになる。

ここでL2正則化のworst concavityを見てみると、負～0の値をとっているが、元のデータを俯瞰すると良性の集団の方が全体的に高い値を示していて矛盾している。一方、L1正則化の場合は、C=0.001で全ての係数がゼロとなっていて、結果に影響していないことを示唆している。

L1正則化で正則化の程度を弱めて、C=1, 0.5, 0.1としてみると、worst concavityは結局ゼロとなるが、worst textureは一貫して負の値を維持している。この傾向はarea errorにも僅かだが見られる。

cancerデータを俯瞰してみると、worst textureは良性・悪性の分布がかなり重なっていて、悪性のデータのボリュームが大きい。area errorも両クラスのデータが近く、値が小さく、良性のデータ量が卓越している。

ヒストグラムを見る限りほとんどの特性量の値が大きいときに良性を示唆しているようみ見えるが、Logistic回帰の結果からは、多くの特性量が効いておらず、中には分布からの推測と逆の傾向を示す。

scikit-learn – LogisticRegression

2020-05-17 / tau / コメントする

概要

scikit-learnのLogisticRegressionモデルはLogistic回帰のモデルを提供する。利用方法の概要は以下の手順で、LinearRegressionなど他の線形モデルとほぼ同じだが、モデルインスタンス生成時に与える正則化パラメーターCはRidge/Lassoのalphaと逆で、正則化の効果を強くするにはCを小さくする（Cを大きくすると正則化が弱まり、訓練データに対する精度は高まるが過学習の可能性が高くなる）。

また、正則化の方法をL1正則化、L2正則化、Elastic netから選択できる。

LogisticRegressのクラスをインポートする
ハイパーパラメーターC、正則化方法、solver（収束計算方法）などを指定し、モデルのインスタンスを生成する
fit()メソッドに訓練データを与えて学習させる

学習済みのモデルの利用方法は以下の通り。

score()メソッドにテストデータを与えて適合度を計算する
predict()メソッドに説明変数を与えてターゲットを予測
モデルインスタンスのプロパティーからモデルのパラメーターを利用
- 切片はintercept_、重み係数はcoef_(末尾のアンダースコアに注意)

利用例

以下は、breast_cancerデータセットに対してLogisticRegressionを適用した例。デフォルトのsolverは'lbfgs'でデフォルトの最大収束回数(100)では収束しなかったため、max_iter=3000を指定している。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(
    ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression(max_iter=3000).fit(X_train, y_train)
print("")
print("Training score: {}".format(logreg.score(X_train, y_train)))
print("Test score    : {}".format(logreg.score(X_test, y_test)))
print("Prediction")
for i in range(3):
    print("{} -> {}".format(y_test[i], logreg.predict(X_test[i].reshape(1, -1))))

# Training score: 0.9577464788732394
# Test score    : 0.958041958041958
# Prediction
# 1 -> [1]
# 0 -> [0]
# 1 -> [1]

from sklearn.datasets import load_breast_cancer

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression

ds = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

ds.data, ds.target, stratify=ds.target, random_state=42)

logreg = LogisticRegression(max_iter=3000).fit(X_train, y_train)

print("")

print("Training score: {}".format(logreg.score(X_train, y_train)))

print("Test score : {}".format(logreg.score(X_test, y_test)))

print("Prediction")

for i in range(3):

print("{} -> {}".format(y_test[i], logreg.predict(X_test[i].reshape(1, -1))))

# Training score: 0.9577464788732394

# Test score : 0.958041958041958

# Prediction

# 1 -> [1]

# 0 -> [0]

# 1 -> [1]

利用方法

LogisticRgressionの主な利用方法はLineaRegressionとほとんど同じで、以下は特有の設定を中心にまとめる。

モデルクラスのインポート

scikit-learn.linear_modelパッケージからLogisticRegressonクラスをインポートする。

from sklearn.linear_model import LogisticRegression

1	from sklearn.linear_model import LogisticRegression

モデルのインスタンスの生成

LogisticRegressionでは、ハイパーパラメーターCによって正則化の強さを指定する。このCはRidge/Lassoのalphaと異なり、正則化の効果を強めるためには値を小さくする。デフォルトはC=1.0。

logreg = LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0,
             fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,
             solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False,
             n_jobs=None, l1_ratio=None)

logreg = LogisticRegression(penalty='l2', *, dual=False, tol=0.0001, C=1.0,

fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None,

solver='lbfgs', max_iter=100, multi_class='auto', verbose=0, warm_start=False,

n_jobs=None, l1_ratio=None)

以下、RidgeとLassoに特有のパラメーターのみ説明。LinearRegressionと共通のパラメーターはLinearRegressionを参照。

penalty: 'l1', 'l2', 'elasticnet', 'none'で正則化項のノルムのタイプを指定する。ソルバーの'newton-cg','sag','lbfgs'はL2正則化のみサポートし、'elasticnet'は'saga'のみがサポートする。デフォルトは'none'で正則化は適用されない('liblinear'は'none'に対応しない)。
tol: 収束計算の解の精度で、デフォルトは1e-4。
C: 正則化の強さの逆数。正の整数で指定し、デフォルトは1.0。
solver: 'newton-cg'、'lbfgs'、'liblinear'、'sag'、'saga'のうちから選択される。デフォルトは'lbfgs'。小さなデータセットには'liblnear'が適し、大きなデータセットに対しては'sag'、'saga'の計算が速い。複数クラスの問題には、'newton-cg'、'sag'、'saga'、'lbfgs'が対応し、'liblinear'は一対他しか対応しない。その他ノルムの種類とソルバーの対応。
max_iter: 収束計算の制限回数を指定する。デフォルト値は100。
random_state: データをシャッフルする際のランダム・シードで、solver='sag'の際に用いる。
l1_ratio: Elastic-Netのパラメーター。[0, 1]の値で、penalty='elasticnet'の時のみ使われる。

モデルの学習

fit()メソッドに特徴量とターゲットの訓練データを与えてモデルに学習させる(回帰係数を決定する)。

lr.fit(X, y)

1	lr.fit(X, y)

X: 特徴量の配列。2次元配列で、各列が各々の説明変数に対応し、行数はデータ数を想定している。変数が1つで1次元配列の時はreshape(-1, 1)かスライス([:, n:n+1])を使って1列の列ベクトルに変換する必要がある。
y: ターゲットの配列で、通常は1変数で1次元配列。

3つ目の引数sample_weightは省略。

適合度の計算

score()メソッドに特徴量とターゲットを与えて適合度を計算する。

lr.score(X, y)

1	lr.score(X, y)

その他のメソッド

decision_function(X)
densiffy()
predict_proba(X)
predict_log_proba()
sparsify()

Logistic回帰～forgeデータ～Pythonではじめる機械学習より

2020-05-17 / tau / コメントする

概要

O’REILLYの書籍”Pythonではじめる機械学習”の2.3.3.5、Logistic回帰でforgeデータの決定境界をトレースしてみたとき、収束計算のソルバーの違いや、元データと書籍のデータの違いなどから再現性に悩んだので記録しておく。

決定境界

mglearnのforgeデータセットに対してLogisticRegressionを適用してみる。

Cがかなり大きい場合、すなわち正則をほとんど行わない場合には、与えられたデータに対して可能な限り適合させようとしており、データに対する適合度は高い。Cが小さくなると正則化が効いてきて、データ全体に対して適合させようとしているように見える。

ここで上の図のC=1のケースは、書籍の図2-15右側と比べると決定境界の勾配が逆になっている。その理由は次のようであることが分かった。

書籍ではLogisticRegression()の収束手法を指定せず、デフォルトのsolver='liblinear'が使用されている
今回指定なしで実行したところ、以下のような警告が発生
- FutureWarning: Default solver will be changed to ‘lbfgs’ in 0.22. Specify a solver to silence this warning.
  FutureWarning)
- デフォルトのソルバーが（現在はliblinearだが）ver 0.22ではlbfgsになる／このwarningを黙らせるためにソルバーを指定せよ
そこでモデルのインスタンス生成時にLogisticRegression(solver='lbfgs')としたところ先の結果となった
指定なし、あるいはsolver='liblinear'とすると書籍と同じ結果になる

liblinearによる結果が以下の通り。正則化の度合いに応じてlbfgsよりも傾きがダイナミックに変わっているように見える。

なお、これらの図の傾きについて、今度は書籍の図2-16と随分違っている。よく見てみると、同図のforgeデータは特に下側の〇印の点でオリジナルにはないデータがいくつか加わっているためと考えられる。

これらのコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
from mglearn.datasets import make_forge
from sklearn.linear_model import LogisticRegression

X, y = make_forge()

xmin, xmax = 7.5, 12.5
ymin, ymax = -1, 6

C_values = [1e5, 1e2, 1e0, 1e-2]

fig, axs = plt.subplots(2, 2, figsize=(6.4, 6.4))
fig.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -1)

for ax, c in zip(axs_1d[0], C_values):
    logreg = LogisticRegression(C=c, solver='liblinear')
    logreg.fit(X, y)

    b = logreg.intercept_[0]
    w0 = logreg.coef_[0][0]
    w1 = logreg.coef_[0][1]

    x_border = np.linspace(xmin, xmax)
    y_border = (-b - w0 * x_border) / w1

    ax.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='^')
    ax.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='o')

    ax.plot(x_border, y_border, 'k')

    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)

    ax.set_title("C={:2.2f}(score={:6.3f})".format(c, logreg.score(X, y)))
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")
    ax.label_outer()

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mglearn.datasets import make_forge

from sklearn.linear_model import LogisticRegression

X, y = make_forge()

xmin, xmax = 7.5, 12.5

ymin, ymax = -1, 6

C_values = [1e5, 1e2, 1e0, 1e-2]

fig, axs = plt.subplots(2, 2, figsize=(6.4, 6.4))

fig.subplots_adjust(hspace=0.4)

axs_1d = axs.reshape(1, -1)

for ax, c in zip(axs_1d[0], C_values):

logreg = LogisticRegression(C=c, solver='liblinear')

logreg.fit(X, y)

b = logreg.intercept_[0]

w0 = logreg.coef_[0][0]

w1 = logreg.coef_[0][1]

x_border = np.linspace(xmin, xmax)

y_border = (-b - w0 * x_border) / w1

ax.scatter(X[:, 0][y==1], X[:, 1][y==1], marker='^')

ax.scatter(X[:, 0][y==0], X[:, 1][y==0], marker='o')

ax.plot(x_border, y_border, 'k')

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_title("C={:2.2f}(score={:6.3f})".format(c, logreg.score(X, y)))

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

ax.label_outer()

plt.show()

3次元表示

2つのCの値について、二つの特徴量の組み合わせに対する青い点の確率分布を表示してみる(solver='lbfgs')。Cが小さいと確率分布がなだらかになる様子が見て取れるが、データに対する判別の適合度との関係はよくわからない。

import numpy as np
import matplotlib.pyplot as plt
from mglearn.datasets import make_forge
from sklearn.linear_model import LogisticRegression
from mpl_toolkits.mplot3d import Axes3D

X, y = make_forge()

xmin, xmax = 7.5, 12.5
ymin, ymax = -1, 6

gx = np.linspace(xmin, xmax, 40)
gy = np.linspace(ymin, ymax, 40)
gx, gy = np.meshgrid(gx, gy)

C_values = [1e3, 1e-1]

fig = plt.figure(figsize=(12, 4.8))

ax0 = fig.add_subplot(121, projection='3d')
ax1 = fig.add_subplot(122, projection='3d')
axs = [ax0, ax1]

for ax, c in zip(axs, C_values):
    logreg = LogisticRegression(C=c, solver='lbfgs')
    logreg.fit(X, y)

    b = logreg.intercept_[0]
    w0 = logreg.coef_[0][0]
    w1 = logreg.coef_[0][1]
    gz = 1/(1 + np.exp(-b - w0*gx - w1*gy))
    gz05 = np.full_like(gz, 0.5)

    y_border_min = (-b - w0 * xmin) / w1
    y_border_max = (-b - w0 * xmax) / w1

    ax.scatter(X[:, 0][y==1], X[:, 1][y==1], 0.5, color='tab:blue')
    ax.scatter(X[:, 0][y==0], X[:, 1][y==0], 0.5, color='tab:red')
    ax.plot_wireframe(gx, gy, gz, color='tab:green', alpha=0.5)
    ax.plot_surface(gx, gy, gz05, color='k', alpha=0.2)
    ax.plot([xmin, xmax], [y_border_min, y_border_max], 0.5)

    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)

    ax.set_title("C={}".format(c))
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from mglearn.datasets import make_forge

from sklearn.linear_model import LogisticRegression

from mpl_toolkits.mplot3d import Axes3D

X, y = make_forge()

xmin, xmax = 7.5, 12.5

ymin, ymax = -1, 6

gx = np.linspace(xmin, xmax, 40)

gy = np.linspace(ymin, ymax, 40)

gx, gy = np.meshgrid(gx, gy)

C_values = [1e3, 1e-1]

fig = plt.figure(figsize=(12, 4.8))

ax0 = fig.add_subplot(121, projection='3d')

ax1 = fig.add_subplot(122, projection='3d')

axs = [ax0, ax1]

for ax, c in zip(axs, C_values):

logreg = LogisticRegression(C=c, solver='lbfgs')

logreg.fit(X, y)

b = logreg.intercept_[0]

w0 = logreg.coef_[0][0]

w1 = logreg.coef_[0][1]

gz = 1/(1 + np.exp(-b - w0*gx - w1*gy))

gz05 = np.full_like(gz, 0.5)

y_border_min = (-b - w0 * xmin) / w1

y_border_max = (-b - w0 * xmax) / w1

ax.scatter(X[:, 0][y==1], X[:, 1][y==1], 0.5, color='tab:blue')

ax.scatter(X[:, 0][y==0], X[:, 1][y==0], 0.5, color='tab:red')

ax.plot_wireframe(gx, gy, gz, color='tab:green', alpha=0.5)

ax.plot_surface(gx, gy, gz05, color='k', alpha=0.2)

ax.plot([xmin, xmax], [y_border_min, y_border_max], 0.5)

ax.set_xlim(xmin, xmax)

ax.set_ylim(ymin, ymax)

ax.set_title("C={}".format(c))

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

plt.show()

Ridge回帰とLasso回帰

2020-05-16 / tau / コメントする

概要

回帰は、以下のようなm個の特徴量に関するnセットのデータXとそれらに対するターゲット値yについて、xからyを推定するモデルを決定する。

(1) $\begin{equation*} \boldsymbol{X} = \left[ \begin{array}{ccc} x_{11} & \cdots & x_{m1} \\ \vdots & & \vdots \\ x_{1n} & \cdots & x_{mn} \\ \end{array} \right] \left[ \begin{array}{c} y_1 \\ \vdots \\ y_n \end{array} \right] \quad \Rightarrow \quad y = f(\boldsymbol{x}) \end{equation*}$

線形回帰は、モデルの関数形を以下のような特徴量に関する線形式とする。

(2) $\begin{equation*} \hat{y} = w_0 + w_1 x_1 + \cdots + w_m x_m \end{equation*}$

通常線形回帰（重回帰、多重回帰）の場合、これを以下のような最小化問題として解く。

(3) $\begin{equation*} \mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i)^2 \end{equation*}$

通常線形回帰では、全ての訓練データに対する予測誤差を最小化しようとするが、このことで大きく外れた特徴量に対しても何とか合わせようとすることになる。このような状態を過学習と呼び、訓練データに対する予測精度は高くなるが、モデルが訓練データの状態に過敏に反応して、全般的な特徴に対する精度が却って低くなる（過学習～多項式回帰の場合）。

そこで、通常線形回帰の最適化に対して、全体的に重み係数の影響を小さくするための正則化項（罰金項、ペナルティー項）を考慮する。通常、ペナルティー項としては重み係数のノルムが用いられる（右辺第1項や第2項に分数の係数をつけることがあるが、計算の便宜のためであり本質への影響はない）。

(4) $\begin{equation*} \mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i) + \alpha \sum_j |w_j|^p \end{equation*}$

正則化項が重みの大きさを制限しようとするものであること、この式がこれを制約とした制約条件付き最適化問題であることは正則化の意味にまとめた。

このノルムにおいて、p=1(L1ノルム)の場合をLasso回帰、p=2(L2ノルム)の場合をRidge回帰と呼び、重みに対する制限のほかに以下のような特徴がある。

Ridge回帰: 特徴量間の相関が高い場合～多重共線性(multicolinearity)が強い場合や一時従属な場合、通常線形回帰では解が求まらなかったりモデルが不安定になるが、Ridge回帰は何とか解を求められるようになる。
Lasso回帰: 多数の特徴量のうち効果が小さいものの係数がゼロになり、モデルの複雑さを緩和できる。

Ridge回帰

Ridge回帰は、多重線形回帰の最適化において重み係数のL2ノルムを正則化項として付加する。

(5) $\begin{align*} &\mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i) + \alpha \sum_j |w_j|^2 \\ & \mathrm{where} \quad \hat{y}_i = w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} \end{align*}$

Ridge回帰は、特徴量の重みの強さを制限する（係数の絶対値を小さくする）効果を持つとともに、特徴量間の線形性が強い場合は予測式が不安定になることを防ぐ。

Ridge回帰の解析的な理解

Lasso回帰

Lasso回帰は、多重線形回帰の最適化において重み係数のL1ノルムを正則化項として付加する。

(6) $\begin{align*} &\mathrm{minimize} \quad \sum_i (y_i - \hat{y}_i) + \alpha \sum_j |w_j| \\ & \mathrm{where} \quad \hat{y}_i = w_0 + w_1 x_{1i} + \cdots + w_m x_{mi} \end{align*}$

Lasso回帰もRidge回帰と同じく、特徴量の係数の重みを制限するが、正則化を強めるとともに係数がゼロとなり、モデルがシンプルになるという特性がある。

Lasso回帰の解析的な理解

Ridge回帰とLasso回帰の挙動

係数の大きさ

Pythonのscikit-learnで得られる糖尿病に関するdiabetesデータセットを使って、同じくscikit-learnのRidge回帰モデルとLasso回帰モデルの挙動を比べてみる。alphaを大きくして正則化を強めるほど、全体的に係数の絶対値が小さくなっている。Ridgeの場合は必ずしも係数をゼロにしないのでモデルの複雑さが残るのに対して、Lassoの場合、係数は正則化が強いほど多くの係数がゼロになりモデルがシンプルになる。

alphaの増加に伴うRidgeのスコアは以下の通りで、そもそも訓練データに対するスコアが低い。もともと10個程度の特徴量ではそれほどの精度が期待できないようだ。

LinearRegression
 training score: 0.555
 test score    : 0.359
Ridge(alpha=0.1)
 training score: 0.550
 test score    : 0.369
Ridge(alpha=1)
 training score: 0.463
 test score    : 0.357
Ridge(alpha=10)
 training score: 0.171
 test score    : 0.143

LinearRegression

training score: 0.555

test score : 0.359

Ridge(alpha=0.1)

training score: 0.550

test score : 0.369

Ridge(alpha=1)

training score: 0.463

test score : 0.357

Ridge(alpha=10)

training score: 0.171

test score : 0.143

Lassoのスコアも同様に低い。alpha=10ではLasso回帰の特性から全ての係数がゼロとなり、相関係数がゼロとなっている。

Lasso(alpha=0.1)
 training score: 0.548
 test score    : 0.355
Lasso(alpha=1)
 training score: 0.414
 test score    : 0.278
Lasso(alpha=10)
 training score: 0.000
 test score    : -0.000

Lasso(alpha=0.1)

training score: 0.548

test score : 0.355

Lasso(alpha=1)

training score: 0.414

test score : 0.278

Lasso(alpha=10)

training score: 0.000

test score : -0.000

この計算に用いたPythonのコードは以下の通り。

import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso

alphas = [0.1, 1, 10]
markers = ['2', '3', '1']

ds = load_diabetes()

X_train, X_test, y_train, y_test =\
    train_test_split(ds.data, ds.target, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)
print("LinearRegression")
print(" training score: {:5.3f}".format(lr.score(X_train, y_train)))
print(" test score    : {:5.3f}".format(lr.score(X_test, y_test)))

fig = plt.figure(figsize=(12, 4.8))
x_scatter = list(range(len(ds.feature_names)))

ax1 = fig.add_subplot(121)
ax1.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',
    label="LinearRegression")
for alpha, marker in zip(alphas, markers):
    rg = Ridge(alpha=alpha)
    rg.fit(X_train, y_train)
    print("Ridge(alpha={})".format(alpha))
    print(" training score: {:5.3f}".format(rg.score(X_train, y_train)))
    print(" test score    : {:5.3f}".format(rg.score(X_test, y_test)))
    ax1.scatter(x_scatter, rg.coef_, marker=marker, s=60,
        label="alpha={}".format(alpha))
    ax1.spines['top'].set_visible(False)
    ax1.spines['bottom'].set_position('zero')
    ax1.set_xticks(x_scatter)
    ax1.set_xticklabels(ds.feature_names, alpha=0.75)
ax1.legend()
ax1.set_title("Ridge")

ax2 = fig.add_subplot(122)
ax2.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',
    label="LinearRegression")
for alpha, marker in zip(alphas, markers):
    ls = Lasso(alpha=alpha)
    ls.fit(X_train, y_train)
    print("Lasso(alpha={})".format(alpha))
    print(" training score: {:5.3f}".format(ls.score(X_train, y_train)))
    print(" test score    : {:5.3f}".format(ls.score(X_test, y_test)))
    ax2.scatter(x_scatter, ls.coef_, marker=marker, s=60,
        label="alpha={}".format(alpha))
    ax2.spines['top'].set_visible(False)
    ax2.spines['bottom'].set_position('zero')
    ax2.set_xticks(x_scatter)
    ax2.set_xticklabels(ds.feature_names, alpha=0.75)
ax2.legend()
ax2.set_title("Lasso")

plt.show()

import matplotlib.pyplot as plt

from sklearn.datasets import load_diabetes

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.linear_model import Ridge

from sklearn.linear_model import Lasso

alphas = [0.1, 1, 10]

markers = ['2', '3', '1']

ds = load_diabetes()

X_train, X_test, y_train, y_test =\

train_test_split(ds.data, ds.target, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("LinearRegression")

print(" training score: {:5.3f}".format(lr.score(X_train, y_train)))

print(" test score : {:5.3f}".format(lr.score(X_test, y_test)))

fig = plt.figure(figsize=(12, 4.8))

x_scatter = list(range(len(ds.feature_names)))

ax1 = fig.add_subplot(121)

ax1.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',

label="LinearRegression")

for alpha, marker in zip(alphas, markers):

rg = Ridge(alpha=alpha)

rg.fit(X_train, y_train)

print("Ridge(alpha={})".format(alpha))

print(" training score: {:5.3f}".format(rg.score(X_train, y_train)))

print(" test score : {:5.3f}".format(rg.score(X_test, y_test)))

ax1.scatter(x_scatter, rg.coef_, marker=marker, s=60,

label="alpha={}".format(alpha))

ax1.spines['top'].set_visible(False)

ax1.spines['bottom'].set_position('zero')

ax1.set_xticks(x_scatter)

ax1.set_xticklabels(ds.feature_names, alpha=0.75)

ax1.legend()

ax1.set_title("Ridge")

ax2 = fig.add_subplot(122)

ax2.scatter(x_scatter, lr.coef_, marker='o', s=40, c='w', ec='b',

label="LinearRegression")

for alpha, marker in zip(alphas, markers):

ls = Lasso(alpha=alpha)

ls.fit(X_train, y_train)

print("Lasso(alpha={})".format(alpha))

print(" training score: {:5.3f}".format(ls.score(X_train, y_train)))

print(" test score : {:5.3f}".format(ls.score(X_test, y_test)))

ax2.scatter(x_scatter, ls.coef_, marker=marker, s=60,

label="alpha={}".format(alpha))

ax2.spines['top'].set_visible(False)

ax2.spines['bottom'].set_position('zero')

ax2.set_xticks(x_scatter)

ax2.set_xticklabels(ds.feature_names, alpha=0.75)

ax2.legend()

ax2.set_title("Lasso")

plt.show()

学習曲線

特徴量を増やすために、Boston house-pricesデータセットの特徴量データを拡張して試す。13個の特徴量に加えて、それらの特徴量同士の積から新たな特徴量を生成する。その結果、全体の特徴量数は単独の特徴量13、各特徴量の2乗が13、2つの特徴量の積が₁₃C₂ = 78の合計で104個となる。この特徴量データとターゲットの住宅価格について訓練データとテストデータに分け、Ridge回帰とLasso回帰のハイパーパラメータalphaを変化させてスコアの変化を見たのが以下の図。

Ridge、Lassoとも訓練データのスコアに対してテストデータのスコアは低く、過学習の様子がわかる。Ridgeではalpha=100程度でテストデータのスコアが最も高く0.75程度となる。Lassoの方はalpha=0.1程度でテストデータのスコアが最も高く、これも0.75を少し上回る程度。またLassoについては、alphaを増やしていくとゼロとなる係数の数が増えていき、それに伴って訓練データのスコアも下がっている。

Boston house-pricesデータに対して、RidgeとLassoの2つのモデルのみを検討するなら、計算コストがより少ないLasso回帰でalpha=0.1程度を選択することになろうかと考えられる。

この計算のコードは以下の通り。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso

pow_min = -3
pow_max = 3
pow_num = 20
alpha_exp = np.linspace(pow_min, pow_max, pow_num)
alphas = 10**alpha_exp

ds = load_boston()
X_org = ds.data
y = ds.target

cols = X_org.shape[1]
X = X_org.copy()
for j in range(cols):
    for jj in range(j + 1):
        X = np.hstack((X, (X[:, j] * X[:, jj]).reshape(-1, 1)))

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)
print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))

trn_scores_ridge = np.empty(0)
tst_scores_ridge = np.empty(0)
for alpha in alphas:
    rg = Ridge(alpha=alpha)
    rg.fit(X_train, y_train)
    trn_scores_ridge = np.append(trn_scores_ridge, rg.score(X_train, y_train))
    tst_scores_ridge = np.append(tst_scores_ridge, rg.score(X_test, y_test))

trn_scores_lasso = np.empty(0)
tst_scores_lasso = np.empty(0)
zero_coef = np.empty(0)
n_zero_coef = np.empty(0)
for alpha in alphas:
    ls = Lasso(alpha=alpha)
    ls.fit(X_train, y_train)
    trn_scores_lasso = np.append(trn_scores_lasso, ls.score(X_train, y_train))
    tst_scores_lasso = np.append(tst_scores_lasso, ls.score(X_test, y_test))
    n_zero_coef = np.append(n_zero_coef, ls.coef_[ls.coef_==0].size)

fig = plt.figure(figsize=(12, 4.8))

ax_ridge = fig.add_subplot(121)
ax_ridge.plot(alphas, trn_scores_ridge, label="Training score")
ax_ridge.plot(alphas, tst_scores_ridge, linestyle='dashed', label="Test score")
ax_ridge.set_xscale('log')
ax_ridge.set_ylim(0.5, 1)
ax_ridge.set_xlabel("alpha")
ax_ridge.set_ylabel("score")
ax_ridge.legend()
ax_ridge.set_title("Ridge")

ax_lasso = fig.add_subplot(122)
ax_lasso_coef = ax_lasso.twinx()
ax_lasso.plot(alphas, trn_scores_lasso, label="Training score")
ax_lasso.plot(alphas, tst_scores_lasso, linestyle='dashed', label="Test score")
hscore, lscore = ax_lasso.get_legend_handles_labels()
ax_lasso_coef.plot(alphas, n_zero_coef, linestyle='dotted',
    label="Zero coefficients", c='g')
hcoef, lcoef = ax_lasso_coef.get_legend_handles_labels()
ax_lasso.set_xscale('log')
ax_lasso.set_ylim(0.5, 1)
ax_lasso_coef.set_ylim(0, 100)
ax_lasso.set_xlabel("alpha")
ax_lasso.set_ylabel("score")
ax_lasso.legend(hscore + hcoef, lscore + lcoef, loc='lower center')
ax_lasso.set_title("Lasso")

plt.show()

import numpy as np

import matplotlib.pyplot as plt

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.linear_model import Ridge

from sklearn.linear_model import Lasso

pow_min = -3

pow_max = 3

pow_num = 20

alpha_exp = np.linspace(pow_min, pow_max, pow_num)

alphas = 10**alpha_exp

ds = load_boston()

X_org = ds.data

y = ds.target

cols = X_org.shape[1]

X = X_org.copy()

for j in range(cols):

for jj in range(j + 1):

X = np.hstack((X, (X[:, j] * X[:, jj]).reshape(-1, 1)))

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print(lr.score(X_train, y_train))

print(lr.score(X_test, y_test))

trn_scores_ridge = np.empty(0)

tst_scores_ridge = np.empty(0)

for alpha in alphas:

rg = Ridge(alpha=alpha)

rg.fit(X_train, y_train)

trn_scores_ridge = np.append(trn_scores_ridge, rg.score(X_train, y_train))

tst_scores_ridge = np.append(tst_scores_ridge, rg.score(X_test, y_test))

trn_scores_lasso = np.empty(0)

tst_scores_lasso = np.empty(0)

zero_coef = np.empty(0)

n_zero_coef = np.empty(0)

for alpha in alphas:

ls = Lasso(alpha=alpha)

ls.fit(X_train, y_train)

trn_scores_lasso = np.append(trn_scores_lasso, ls.score(X_train, y_train))

tst_scores_lasso = np.append(tst_scores_lasso, ls.score(X_test, y_test))

n_zero_coef = np.append(n_zero_coef, ls.coef_[ls.coef_==0].size)

fig = plt.figure(figsize=(12, 4.8))

ax_ridge = fig.add_subplot(121)

ax_ridge.plot(alphas, trn_scores_ridge, label="Training score")

ax_ridge.plot(alphas, tst_scores_ridge, linestyle='dashed', label="Test score")

ax_ridge.set_xscale('log')

ax_ridge.set_ylim(0.5, 1)

ax_ridge.set_xlabel("alpha")

ax_ridge.set_ylabel("score")

ax_ridge.legend()

ax_ridge.set_title("Ridge")

ax_lasso = fig.add_subplot(122)

ax_lasso_coef = ax_lasso.twinx()

ax_lasso.plot(alphas, trn_scores_lasso, label="Training score")

ax_lasso.plot(alphas, tst_scores_lasso, linestyle='dashed', label="Test score")

hscore, lscore = ax_lasso.get_legend_handles_labels()

ax_lasso_coef.plot(alphas, n_zero_coef, linestyle='dotted',

label="Zero coefficients", c='g')

hcoef, lcoef = ax_lasso_coef.get_legend_handles_labels()

ax_lasso.set_xscale('log')

ax_lasso.set_ylim(0.5, 1)

ax_lasso_coef.set_ylim(0, 100)

ax_lasso.set_xlabel("alpha")

ax_lasso.set_ylabel("score")

ax_lasso.legend(hscore + hcoef, lscore + lcoef, loc='lower center')

ax_lasso.set_title("Lasso")

plt.show()

Diabetesデータセット

2020-05-16 / tau / コメントする

概要

diabetesデータは、年齢や性別など10個の特徴量と、それらの測定1年後の糖尿病の進行度に関する数値を、442人について集めたデータ。出典は”From Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) “Least Angle Regression,” Annals of Statistics (with discussion), 407-499″。

ここではPythonのscikit-learnにあるdiabetesデータの使い方をまとめる。

データの取得とデータ構造

Pythonで扱う場合、scikit-learn.datasetsモジュールにあるload_diabetes()でデータを取得できる。データはBunchクラスのオブジェクト

from sklearn.datasets import load_diabetes

ds = load_diabetes()

for key, value in zip(ds.keys(), ds.values()):
    print("{}:\n{}\n".format(key, value))

from sklearn.datasets import load_diabetes

ds = load_diabetes()

for key, value in zip(ds.keys(), ds.values()):

print("{}:\n{}\n".format(key, value))

データの構造は辞書型で、442人の糖尿病に関する10個の特徴量をレコードとした配列、442人の測定1年後の糖尿病の進行度を示す数値データの配列など。

data:
[[ 0.03807591  0.05068012  0.06169621 ... -0.00259226  0.01990842
  -0.01764613]
 [-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974
  -0.09220405]
 [ 0.08529891  0.05068012  0.04445121 ... -0.00259226  0.00286377
  -0.02593034]
 ...
 [ 0.04170844  0.05068012 -0.01590626 ... -0.01107952 -0.04687948
   0.01549073]
 [-0.04547248 -0.04464164  0.03906215 ...  0.02655962  0.04452837
  -0.02593034]
 [-0.04547248 -0.04464164 -0.0730303  ... -0.03949338 -0.00421986
   0.00306441]]

target:
[151.  75. 141. 206. 135.  97. 138.  63. 110. 310. 101.  69. 179. 185.
 118. 171. 166. 144.  97. 168.  68.  49.  68. 245. 184. 202. 137.  85.
 131. 283. 129.  59. 341.  87.  65. 102. 265. 276. 252.  90. 100.  55.
  61.  92. 259.  53. 190. 142.  75. 142. 155. 225.  59. 104. 182. 128.
  52.  37. 170. 170.  61. 144.  52. 128.  71. 163. 150.  97. 160. 178.
  48. 270. 202. 111.  85.  42. 170. 200. 252. 113. 143.  51.  52. 210.
  65. 141.  55. 134.  42. 111.  98. 164.  48.  96.  90. 162. 150. 279.
  92.  83. 128. 102. 302. 198.  95.  53. 134. 144. 232.  81. 104.  59.
 246. 297. 258. 229. 275. 281. 179. 200. 200. 173. 180.  84. 121. 161.
  99. 109. 115. 268. 274. 158. 107.  83. 103. 272.  85. 280. 336. 281.
 118. 317. 235.  60. 174. 259. 178. 128.  96. 126. 288.  88. 292.  71.
 197. 186.  25.  84.  96. 195.  53. 217. 172. 131. 214.  59.  70. 220.
 268. 152.  47.  74. 295. 101. 151. 127. 237. 225.  81. 151. 107.  64.
 138. 185. 265. 101. 137. 143. 141.  79. 292. 178.  91. 116.  86. 122.
  72. 129. 142.  90. 158.  39. 196. 222. 277.  99. 196. 202. 155.  77.
 191.  70.  73.  49.  65. 263. 248. 296. 214. 185.  78.  93. 252. 150.
  77. 208.  77. 108. 160.  53. 220. 154. 259.  90. 246. 124.  67.  72.
 257. 262. 275. 177.  71.  47. 187. 125.  78.  51. 258. 215. 303. 243.
  91. 150. 310. 153. 346.  63.  89.  50.  39. 103. 308. 116. 145.  74.
  45. 115. 264.  87. 202. 127. 182. 241.  66.  94. 283.  64. 102. 200.
 265.  94. 230. 181. 156. 233.  60. 219.  80.  68. 332. 248.  84. 200.
  55.  85.  89.  31. 129.  83. 275.  65. 198. 236. 253. 124.  44. 172.
 114. 142. 109. 180. 144. 163. 147.  97. 220. 190. 109. 191. 122. 230.
 242. 248. 249. 192. 131. 237.  78. 135. 244. 199. 270. 164.  72.  96.
 306.  91. 214.  95. 216. 263. 178. 113. 200. 139. 139.  88. 148.  88.
 243.  71.  77. 109. 272.  60.  54. 221.  90. 311. 281. 182. 321.  58.
 262. 206. 233. 242. 123. 167.  63. 197.  71. 168. 140. 217. 121. 235.
 245.  40.  52. 104. 132.  88.  69. 219.  72. 201. 110.  51. 277.  63.
 118.  69. 273. 258.  43. 198. 242. 232. 175.  93. 168. 275. 293. 281.
  72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257.  55.  84.  42.
 146. 212. 233.  91. 111. 152. 120.  67. 310.  94. 183.  66. 173.  72.
  49.  64.  48. 178. 104. 132. 220.  57.]

DESCR:
.. _diabetes_dataset:

Diabetes dataset
----------------

Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.

**Data Set Characteristics:**

  :Number of Instances: 442

  :Number of Attributes: First 10 columns are numeric predictive values

  :Target: Column 11 is a quantitative measure of disease progression one year after baseline

  :Attribute Information:
      - Age
      - Sex
      - Body mass index
      - Average blood pressure
      - S1
      - S2
      - S3
      - S4
      - S5
      - S6

Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).

Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html

For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)

feature_names:
['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

data_filename:
C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\diabetes_data.csv.gz

target_filename:
C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\diabetes_target.csv.gz

data:

[[ 0.03807591 0.05068012 0.06169621 ... -0.00259226 0.01990842

-0.01764613]

[-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974

-0.09220405]

[ 0.08529891 0.05068012 0.04445121 ... -0.00259226 0.00286377

-0.02593034]

...

[ 0.04170844 0.05068012 -0.01590626 ... -0.01107952 -0.04687948

0.01549073]

[-0.04547248 -0.04464164 0.03906215 ... 0.02655962 0.04452837

-0.02593034]

[-0.04547248 -0.04464164 -0.0730303 ... -0.03949338 -0.00421986

0.00306441]]

target:

[151. 75. 141. 206. 135. 97. 138. 63. 110. 310. 101. 69. 179. 185.

118. 171. 166. 144. 97. 168. 68. 49. 68. 245. 184. 202. 137. 85.

131. 283. 129. 59. 341. 87. 65. 102. 265. 276. 252. 90. 100. 55.

61. 92. 259. 53. 190. 142. 75. 142. 155. 225. 59. 104. 182. 128.

52. 37. 170. 170. 61. 144. 52. 128. 71. 163. 150. 97. 160. 178.

48. 270. 202. 111. 85. 42. 170. 200. 252. 113. 143. 51. 52. 210.

65. 141. 55. 134. 42. 111. 98. 164. 48. 96. 90. 162. 150. 279.

92. 83. 128. 102. 302. 198. 95. 53. 134. 144. 232. 81. 104. 59.

246. 297. 258. 229. 275. 281. 179. 200. 200. 173. 180. 84. 121. 161.

99. 109. 115. 268. 274. 158. 107. 83. 103. 272. 85. 280. 336. 281.

118. 317. 235. 60. 174. 259. 178. 128. 96. 126. 288. 88. 292. 71.

197. 186. 25. 84. 96. 195. 53. 217. 172. 131. 214. 59. 70. 220.

268. 152. 47. 74. 295. 101. 151. 127. 237. 225. 81. 151. 107. 64.

138. 185. 265. 101. 137. 143. 141. 79. 292. 178. 91. 116. 86. 122.

72. 129. 142. 90. 158. 39. 196. 222. 277. 99. 196. 202. 155. 77.

191. 70. 73. 49. 65. 263. 248. 296. 214. 185. 78. 93. 252. 150.

77. 208. 77. 108. 160. 53. 220. 154. 259. 90. 246. 124. 67. 72.

257. 262. 275. 177. 71. 47. 187. 125. 78. 51. 258. 215. 303. 243.

91. 150. 310. 153. 346. 63. 89. 50. 39. 103. 308. 116. 145. 74.

45. 115. 264. 87. 202. 127. 182. 241. 66. 94. 283. 64. 102. 200.

265. 94. 230. 181. 156. 233. 60. 219. 80. 68. 332. 248. 84. 200.

55. 85. 89. 31. 129. 83. 275. 65. 198. 236. 253. 124. 44. 172.

114. 142. 109. 180. 144. 163. 147. 97. 220. 190. 109. 191. 122. 230.

242. 248. 249. 192. 131. 237. 78. 135. 244. 199. 270. 164. 72. 96.

306. 91. 214. 95. 216. 263. 178. 113. 200. 139. 139. 88. 148. 88.

243. 71. 77. 109. 272. 60. 54. 221. 90. 311. 281. 182. 321. 58.

262. 206. 233. 242. 123. 167. 63. 197. 71. 168. 140. 217. 121. 235.

245. 40. 52. 104. 132. 88. 69. 219. 72. 201. 110. 51. 277. 63.

118. 69. 273. 258. 43. 198. 242. 232. 175. 93. 168. 275. 293. 281.

72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257. 55. 84. 42.

146. 212. 233. 91. 111. 152. 120. 67. 310. 94. 183. 66. 173. 72.

49. 64. 48. 178. 104. 132. 220. 57.]

DESCR:

.. _diabetes_dataset:

Diabetes dataset

----------------

Ten baseline variables, age, sex, body mass index, average blood

pressure, and six blood serum measurements were obtained for each of n =

442 diabetes patients, as well as the response of interest, a

quantitative measure of disease progression one year after baseline.

**Data Set Characteristics:**

:Number of Instances: 442

:Number of Attributes: First 10 columns are numeric predictive values

:Target: Column 11 is a quantitative measure of disease progression one year after baseline

:Attribute Information:

- Age

- Sex

- Body mass index

- Average blood pressure

- S1

- S2

- S3

- S4

- S5

- S6

Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).

Source URL:

https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html

For more information see:

Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.

(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)

feature_names:

['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']

data_filename:

C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\diabetes_data.csv.gz

target_filename:

C:\Users\tomo\AppData\Local\Programs\Python\Python37-32\lib\site-packages\sklearn\datasets\data\diabetes_target.csv.gz

データのキーは以下のようになっている。

from sklearn.datasets import load_diabetes

ds = load_diabetes()

print(ds.keys())

# ddict_keys(['data', 'target', 'DESCR', 'feature_names', 'data_filename', 'target_filename'])

from sklearn.datasets import load_diabetes

ds = load_diabetes()

print(ds.keys())

# ddict_keys(['data', 'target', 'DESCR', 'feature_names', 'data_filename', 'target_filename'])

データの内容

`'data'`～特徴量データセット

10個の特徴量を列とし、442人の被検者を業とした2次元配列。DESCRに説明されているように、これらのデータは標本平均と標本分散で正規化されており、各特徴量とも、データの和はゼロ（正確には1×10^-14～1×10^-13のオーダーの実数）、2乗和は1となる。

data:
[[ 0.03807591  0.05068012  0.06169621 ... -0.00259226  0.01990842
  -0.01764613]
 [-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974
  -0.09220405]
 [ 0.08529891  0.05068012  0.04445121 ... -0.00259226  0.00286377
  -0.02593034]
 ...
 [ 0.04170844  0.05068012 -0.01590626 ... -0.01107952 -0.04687948
   0.01549073]
 [-0.04547248 -0.04464164  0.03906215 ...  0.02655962  0.04452837
  -0.02593034]
 [-0.04547248 -0.04464164 -0.0730303  ... -0.03949338 -0.00421986
   0.00306441]]

data:

[[ 0.03807591 0.05068012 0.06169621 ... -0.00259226 0.01990842

-0.01764613]

[-0.00188202 -0.04464164 -0.05147406 ... -0.03949338 -0.06832974

-0.09220405]

[ 0.08529891 0.05068012 0.04445121 ... -0.00259226 0.00286377

-0.02593034]

...

[ 0.04170844 0.05068012 -0.01590626 ... -0.01107952 -0.04687948

0.01549073]

[-0.04547248 -0.04464164 0.03906215 ... 0.02655962 0.04452837

-0.02593034]

[-0.04547248 -0.04464164 -0.0730303 ... -0.03949338 -0.00421986

0.00306441]]

`'target'`～糖尿病の進行度

442人に関する10個の特徴量データを測定した1年後の糖尿病の進行度を示す数値。原文でも”a measure of disease progression one year after baseline”としか示されていない。このデータは正規化されていない。

target:
[151.  75. 141. 206. 135.  97. 138.  63. 110. 310. 101.  69. 179. 185.
 118. 171. 166. 144.  97. 168.  68.  49.  68. 245. 184. 202. 137.  85.
 131. 283. 129.  59. 341.  87.  65. 102. 265. 276. 252.  90. 100.  55.
.....
  72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257.  55.  84.  42.
 146. 212. 233.  91. 111. 152. 120.  67. 310.  94. 183.  66. 173.  72.
  49.  64.  48. 178. 104. 132. 220.  57.]

target:

[151. 75. 141. 206. 135. 97. 138. 63. 110. 310. 101. 69. 179. 185.

118. 171. 166. 144. 97. 168. 68. 49. 68. 245. 184. 202. 137. 85.

131. 283. 129. 59. 341. 87. 65. 102. 265. 276. 252. 90. 100. 55.

.....

72. 140. 189. 181. 209. 136. 261. 113. 131. 174. 257. 55. 84. 42.

146. 212. 233. 91. 111. 152. 120. 67. 310. 94. 183. 66. 173. 72.

49. 64. 48. 178. 104. 132. 220. 57.]

`'feature_names'`～特徴名

10種類の特徴量の名称

	sklearn	R
0	age	age	年齢
1	sex	sex	性別
2	bmi	bmi	BMI(Body Mass Index)
3	bp	map	(動脈の)平均血圧(Average blood pressure)
4	S1	tc	総コレステロール？
5	S2	ldl	悪玉コレステロール(Low Density Lipoprotein)
6	S3	hdl	善玉コレステロール(High Density Lipoprotein)
7	S4	tch	総コレステロール？
8	S5	ltg	ラモトリギン？
9	S6	glu	血糖＝グルコース？

scikit-learnでは後半のデータがs1～s6とだけ表示されていて、DESCRにおいても”six blood serum measurements”とだけ書かれている。Rのデータセットでは、これらがtc, ldlなど血清に関する指標の略号で示されている。

tcとtchはどちらも総コレステロールに関するデータのようだが、どういう違いなのかよくわからない。少なくとも双方に正の相関があるが、ばらつきは大きい。

`'filename'`～ファイル名

CSVファイルのフルパス名が示されている。scikit-learnの他のデータセットと以下の2点が異なっている。

特徴量データdiabetes_data.csvとターゲットデータdiabetes_target.csvの2つのファイルに分かれている
ファイルの拡張子がcsvとなっているが、区切りはスペースとなっている

data_filename:
C:...\lib\site-packages\sklearn\datasets\data\diabetes_data.csv.gz

target_filename:
C:...\lib\site-packages\sklearn\datasets\data\diabetes_target.csv.gz

data_filename:

C:...\lib\site-packages\sklearn\datasets\data\diabetes_data.csv.gz

target_filename:

C:...\lib\site-packages\sklearn\datasets\data\diabetes_target.csv.gz

diabetes_data.csv

1行に10個の実数がスペース区切りで配置されており、442行のデータがある。442人分の10個の特徴量データ

3.807590643342410180e-02 5.068011873981870252e-02 6.169620651868849837e-02 2.187235499495579841e-02 -4.422349842444640161e-02 -3.482076283769860309e-02 -4.340084565202689815e-02 -2.592261998182820038e-03 1.990842087631829876e-02 -1.764612515980519894e-02
-1.882016527791040067e-03 -4.464163650698899782e-02 -5.147406123880610140e-02 -2.632783471735180084e-02 -8.448724111216979540e-03 -1.916333974822199970e-02 7.441156407875940126e-02 -3.949338287409189657e-02 -6.832974362442149896e-02 -9.220404962683000083e-02
8.529890629667830071e-02 5.068011873981870252e-02 4.445121333659410312e-02 -5.670610554934250001e-03 -4.559945128264750180e-02 -3.419446591411950259e-02 -3.235593223976569732e-02 -2.592261998182820038e-03 2.863770518940129874e-03 -2.593033898947460017e-02
.....
4.170844488444359899e-02 5.068011873981870252e-02 -1.590626280073640167e-02 1.728186074811709910e-02 -3.734373413344069942e-02 -1.383981589779990050e-02 -2.499265663159149983e-02 -1.107951979964190078e-02 -4.687948284421659950e-02 1.549073015887240078e-02
-4.547247794002570037e-02 -4.464163650698899782e-02 3.906215296718960200e-02 1.215130832538269907e-03 1.631842733640340160e-02 1.528299104862660025e-02 -2.867429443567860031e-02 2.655962349378539894e-02 4.452837402140529671e-02 -2.593033898947460017e-02
-4.547247794002570037e-02 -4.464163650698899782e-02 -7.303030271642410587e-02 -8.141376581713200000e-02 8.374011738825870577e-02 2.780892952020790065e-02 1.738157847891100005e-01 -3.949338287409189657e-02 -4.219859706946029777e-03 3.064409414368320182e-03

3.807590643342410180e-02 5.068011873981870252e-02 6.169620651868849837e-02 2.187235499495579841e-02 -4.422349842444640161e-02 -3.482076283769860309e-02 -4.340084565202689815e-02 -2.592261998182820038e-03 1.990842087631829876e-02 -1.764612515980519894e-02

-1.882016527791040067e-03 -4.464163650698899782e-02 -5.147406123880610140e-02 -2.632783471735180084e-02 -8.448724111216979540e-03 -1.916333974822199970e-02 7.441156407875940126e-02 -3.949338287409189657e-02 -6.832974362442149896e-02 -9.220404962683000083e-02

8.529890629667830071e-02 5.068011873981870252e-02 4.445121333659410312e-02 -5.670610554934250001e-03 -4.559945128264750180e-02 -3.419446591411950259e-02 -3.235593223976569732e-02 -2.592261998182820038e-03 2.863770518940129874e-03 -2.593033898947460017e-02

.....

4.170844488444359899e-02 5.068011873981870252e-02 -1.590626280073640167e-02 1.728186074811709910e-02 -3.734373413344069942e-02 -1.383981589779990050e-02 -2.499265663159149983e-02 -1.107951979964190078e-02 -4.687948284421659950e-02 1.549073015887240078e-02

-4.547247794002570037e-02 -4.464163650698899782e-02 3.906215296718960200e-02 1.215130832538269907e-03 1.631842733640340160e-02 1.528299104862660025e-02 -2.867429443567860031e-02 2.655962349378539894e-02 4.452837402140529671e-02 -2.593033898947460017e-02

-4.547247794002570037e-02 -4.464163650698899782e-02 -7.303030271642410587e-02 -8.141376581713200000e-02 8.374011738825870577e-02 2.780892952020790065e-02 1.738157847891100005e-01 -3.949338287409189657e-02 -4.219859706946029777e-03 3.064409414368320182e-03

diabetes_target.csv

ターゲットyに相当する442行の実数データ。

1.510000000000000000e+02
7.500000000000000000e+01
1.410000000000000000e+02
.....
1.320000000000000000e+02
2.200000000000000000e+02
5.700000000000000000e+01

1.510000000000000000e+02

7.500000000000000000e+01

1.410000000000000000e+02

.....

1.320000000000000000e+02

2.200000000000000000e+02

5.700000000000000000e+01

‘DESCR’～データセットの説明

データセットの説明。各特徴量データが標準化されていることが説明されている。

Python - diabetes_01_DESCR.py:5
.. _diabetes_dataset:

Diabetes dataset
----------------

Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.

**Data Set Characteristics:**

  :Number of Instances: 442

  :Number of Attributes: First 10 columns are numeric predictive values

  :Target: Column 11 is a quantitative measure of disease progression one year after baseline

  :Attribute Information:
      - Age
      - Sex
      - Body mass index
      - Average blood pressure
      - S1
      - S2
      - S3
      - S4
      - S5
      - S6

Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).

Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html

For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)
[Finished in 1.105s]

Python - diabetes_01_DESCR.py:5

.. _diabetes_dataset:

Diabetes dataset

----------------

Ten baseline variables, age, sex, body mass index, average blood

pressure, and six blood serum measurements were obtained for each of n =

442 diabetes patients, as well as the response of interest, a

quantitative measure of disease progression one year after baseline.

**Data Set Characteristics:**

:Number of Instances: 442

:Number of Attributes: First 10 columns are numeric predictive values

:Target: Column 11 is a quantitative measure of disease progression one year after baseline

:Attribute Information:

- Age

- Sex

- Body mass index

- Average blood pressure

- S1

- S2

- S3

- S4

- S5

- S6

Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).

Source URL:

https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html

For more information see:

Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.

(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)

[Finished in 1.105s]

データの利用

各データの取得方法

data、targetなどのデータを取り出すのに、以下の2つの方法がある。

辞書のキーを使って呼び出す（例：diabetes['data']）
キーの文字列をプロパティーに指定する（例：diabetes.data）

dataの扱い

そのまま2次元配列として扱うか、pandas.DataFrameで扱う。特定の特徴量データを取り出すには、ファンシー・インデックスを使う。

from sklearn.datasets import load_diabetes
from pandas import DataFrame

ds = load_diabetes()
df = DataFrame(ds.data, columns=ds.feature_names)

print(df[['s1', 's4']])

#            s1        s4
# 0   -0.044223 -0.002592
# 1   -0.008449 -0.039493
# 2   -0.045599 -0.002592
# 3    0.012191  0.034309
# 4    0.003935 -0.002592
# ..        ...       ...
# 437 -0.005697 -0.002592
# 438  0.049341  0.034309
# 439 -0.037344 -0.011080
# 440  0.016318  0.026560
# 441  0.083740 -0.039493

from sklearn.datasets import load_diabetes

from pandas import DataFrame

ds = load_diabetes()

df = DataFrame(ds.data, columns=ds.feature_names)

print(df[['s1', 's4']])

# s1 s4

# 0 -0.044223 -0.002592

# 1 -0.008449 -0.039493

# 2 -0.045599 -0.002592

# 3 0.012191 0.034309

# 4 0.003935 -0.002592

# .. ... ...

# 437 -0.005697 -0.002592

# 438 0.049341 0.034309

# 439 -0.037344 -0.011080

# 440 0.016318 0.026560

# 441 0.083740 -0.039493

過学習～多項式回帰の場合

2020-05-14 / tau / コメントする

概要

過学習(over fitting)の例として、多項式の係数を線形回帰で予測した場合の挙動をまとめてみた。

複数の点(x_i, y_i)に対して、以下の線形式の項数を変化させて、Pythonのパッケージ、scikit-learnにあるLinearRegressionでフィッティングさせてみる。

(1) $\begin{equation*} \hat{y} = w_0 + \sum_{j=1}\m w_j x^j \end{equation*}$

データ数が少ない場合

以下の例は、[-3, 1]の間で等間隔な4つの値を発生させ、(x, e^x)となる4つの点を準備、これらのデータセットに対して、多項式の項数（すなわちxの次数）を1～6まで変化させてフィッティングした結果。たとえばn_terms=3の場合は $y = w_0 + w_1 x + w_2 x^2 + w_3 x^3$ の4つの係数を決定することになる。

n_terms=1の場合は単純な線形関数で、データセットの曲線関係を表しているとは言えない。
n_terms=2になるとかなり各点にフィットしているが、x < −1の範囲で本来の関数の値と離れていく。
n_terms=3はデータ数より項数（特徴量の数）が1つ少ない。各点にほぼぴったり合っていて、最も「それらしい」（ただしデータセットの外側の範囲でも合っているとは限らない／指数関数に対してxの有限の多項式ではどこかで乖離していく）
n_terms=4はデータ数と項数（特徴量の数）が等しい。予測曲線がすべての点を通っているが、無理矢理合わせている感があり、データセットの左側で関数形が跳ね上がっている。
n_terms=5はデータ数より特徴量数の方が多くなる。予測曲線は全ての点を通っているが、1番目の点と2番目の点の間で若干曲線が歪んでいる
n_terms=6になると歪が大きくなる

上記の実行コードは以下の通り。

7～8行目は、切片・係数のセットとxの値を与えて多項式の値を計算する関数。
19行目でn_data=4個のxの値を発生させ、20行目で指数関数の値を計算している。後のために乱数でばらつかせる準備をしているが、ここではばらつかせていない
23～24行目でxⁿの特徴量を生成している
35行目で線形回帰モデルのフィッティングを行っている。n_termsで指定した項数（＝次数）までをフィッティングに使っている。
36行目で、フィッティングの結果予測された切片と係数を使って、予測曲線の値を計算している。

import numpy as np
import random as rnd
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

def poly(intercept, coef, x):
    return intercept + sum([w * x**(n + 1) for n, w in enumerate(coef)])

rnd.seed(0)
xmin, xmax = -3, 1
xlim_min, xlim_max = -4, 2
ylim_min, ylim_max = -2, 4

n_data = 4
n_features = 20
n_terms_list = [1, 2, 3, 4, 5, 6]

x = np.linspace(xmin, xmax, n_data)
y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]

df = pd.DataFrame(y, columns=['y'])
for n in range(n_features):
    df["x^{}".format(n+1)] = x**(n+1)
print(df)

fig, axs = plt.subplots(2, 3, figsize=(12, 6.4))
axs_1d = axs.reshape(1, -1)[0]

linreg = LinearRegression()

x_graph = np.linspace(xlim_min, xlim_max)

for ax, n_terms in zip(axs_1d, n_terms_list):
    linreg.fit(df.iloc[:, 1:n_terms+1], df['y'])
    y_linreg = poly(linreg.intercept_, linreg.coef_, x_graph)
    ax.scatter(df['x^1'], df['y'], c='r', zorder=10)
    ax.plot(x_graph, y_linreg, c='gray', linewidth=2,
        label="n_terms={}".format(n_terms))

    ax.set_xlim(xlim_min, xlim_max)
    ax.set_ylim(ylim_min, ylim_max)
    ax.set_aspect('equal')
    ax.legend(loc='upper left')

plt.show()

import numpy as np

import random as rnd

import pandas as pd

from sklearn.linear_model import LinearRegression

import matplotlib.pyplot as plt

def poly(intercept, coef, x):

return intercept + sum([w * x**(n + 1) for n, w in enumerate(coef)])

rnd.seed(0)

xmin, xmax = -3, 1

xlim_min, xlim_max = -4, 2

ylim_min, ylim_max = -2, 4

n_data = 4

n_features = 20

n_terms_list = [1, 2, 3, 4, 5, 6]

x = np.linspace(xmin, xmax, n_data)

y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]

df = pd.DataFrame(y, columns=['y'])

for n in range(n_features):

df["x^{}".format(n+1)] = x**(n+1)

print(df)

fig, axs = plt.subplots(2, 3, figsize=(12, 6.4))

axs_1d = axs.reshape(1, -1)[0]

linreg = LinearRegression()

x_graph = np.linspace(xlim_min, xlim_max)

for ax, n_terms in zip(axs_1d, n_terms_list):

linreg.fit(df.iloc[:, 1:n_terms+1], df['y'])

y_linreg = poly(linreg.intercept_, linreg.coef_, x_graph)

ax.scatter(df['x^1'], df['y'], c='r', zorder=10)

ax.plot(x_graph, y_linreg, c='gray', linewidth=2,

label="n_terms={}".format(n_terms))

ax.set_xlim(xlim_min, xlim_max)

ax.set_ylim(ylim_min, ylim_max)

ax.set_aspect('equal')

ax.legend(loc='upper left')

plt.show()

異常値がある場合

上記の整然とした指数関数のデータに1つだけ飛び離れた異常値を入れてみる。

x = np.linspace(xmin, xmax, n_data)
y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]
x = np.append(x, -1)
y = np.append(y, 2)

x = np.linspace(xmin, xmax, n_data)

y = np.exp(x) + [rnd.uniform(-0.0, 0.0) for n in range(n_data)]

x = np.append(x, -1)

y = np.append(y, 2)

先の例に比べて不安定性＝曲線の振動の度合いが大きくなっている。

データ数を多くした場合

点の数を10個とし、乱数で擾乱を与えてみる（乱数系列も変えている）。

rnd.seed(1)

.....

n_data = 10
n_features = 20
n_terms_list = [1, 3, 5, 7, 9, 13]

x = np.linspace(xmin, xmax, n_data)
y = np.exp(x) + [rnd.uniform(-0.6, 0.6) for n in range(n_data)]

rnd.seed(1)

.....

n_data = 10

n_features = 20

n_terms_list = [1, 3, 5, 7, 9, 13]

x = np.linspace(xmin, xmax, n_data)

y = np.exp(x) + [rnd.uniform(-0.6, 0.6) for n in range(n_data)]

n_terms=5あたりから、全ての点に何とかフィットさせようと曲線が揺れ始め、特徴量数がデータ数と同じ値となる前後から振動が大きくなっている。

scikit-learn – LinearRegression

2020-05-10 / tau / コメントする

概要

scikit-learnのLinearRegressionは、最も単純な多重線形回帰モデルを提供する。

モデルの利用方法の概要は以下の手順。

LinearRegressionのクラスをインポートする
モデルのインスタンスを生成する
fit()メソッドに訓練データを与えて学習させる

学習済みのモデルの利用方法は以下の通り。

score()メソッドにテストデータを与えて適合度を計算する
predict()メソッドに説明変数を与えてターゲットを予測
モデルインスタンスのプロパティーからモデルのパラメーターを利用
- 切片はintercept_、重み係数はcoef_(末尾のアンダースコアに注意)

利用例

配列による場合

以下はscikit-learnのBoston hose pricesデータのうち、2つの特徴量RM(1戸あたり部屋数)とLSTAT(下位層の人口比率)を取り出して、線形回帰のモデルを適用している。

特徴量の一部をとりだすのに、ファンシー・インデックスでリストの要素に2つの変数のインデックスを指定している。また、特徴量データXとターゲットデータyをtrain_test_split()を使って訓練データとテストデータに分けている。

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

ds = load_boston()

X = ds.data[:, [5, 12]]
y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))
print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343
# Prediction for (7, 5):[31.14766768]
# Intercept:-0.6047107435077521
# Coefficients:[ 5.01785312 -0.67451869]

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

ds = load_boston()

X = ds.data[:, [5, 12]]

y = ds.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))

print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343

# Prediction for (7, 5):[31.14766768]

# Intercept:-0.6047107435077521

# Coefficients:[ 5.01785312 -0.67451869]

DataFrameによる場合

以下の例では、データセットの本体(data)をpandasのDataFrameとして構成し、2つの特徴量RMとLSTATを指定して取り出している。

import pandas as pd
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

ds = load_boston()
df = pd.DataFrame(ds.data, columns=ds.feature_names)

X = df[['RM', 'LSTAT']]
y = ds['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))
print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343
# Prediction for (7, 5):[31.14766768]
# Intercept:-0.6047107435077521
# Coefficients:[ 5.01785312 -0.67451869]

import pandas as pd

from sklearn.datasets import load_boston

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

ds = load_boston()

df = pd.DataFrame(ds.data, columns=ds.feature_names)

X = df[['RM', 'LSTAT']]

y = ds['target']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()

lr.fit(X_train, y_train)

print("Score:{}".format(lr.score(X_test, y_test)))

print("Prediction for (7, 5):{}".format(lr.predict([[7, 5]])))

print("Intercept:{}".format(lr.intercept_))

print("Coefficients:{}".format(lr.coef_))

# Score:0.5692445415835343

# Prediction for (7, 5):[31.14766768]

# Intercept:-0.6047107435077521

# Coefficients:[ 5.01785312 -0.67451869]

利用方法

モデルクラスのインポート

scikit-learn.linear_modelパッケージからLinearRegressionクラスをインポートする。

from sklearn.linear_model import LinearRegression

1	from sklearn.linear_model import LinearRegression

モデルのインスタンスの生成

LinearRegressionの場合、ハイパーパラメーターの指定はない。

lr = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

1	lr = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

fit_intercept: 切片を計算しない場合Falseを指定。デフォルトはTrueで切片も計算されるが、原点を通るべき場合にはFalseを指定する。
normalize: Trueを指定すると、特徴量Xが学習の前に正規化(normalize)される(平均を引いてL2ノルムで割る)。デフォルトはFalse。fit_intercept=Falseにセットされた場合は無視される。説明変数を標準化(standardize)する場合はこの引数をFalseにしてsklearn.preprocessing.StandardScalerを使う。
copy_X: Trueを指定するとXはコピーされ、Falseの場合は上書きされる。デフォルトはTrue。
n_jobs: 計算のジョブの数を指定する。デフォルトはNoneで1に相当。n_targets > 1のときのみ適用される。

モデルの学習

fit()メソッドに特徴量とターゲットの訓練データを与えてモデルに学習させる(回帰係数を決定する)。

lr.fit(X, y)

1	lr.fit(X, y)

X: 特徴量の配列。2次元配列で、各列が各々の説明変数に対応し、行数はデータ数を想定している。変数が1つで1次元配列の時はreshape(-1, 1)かスライス([:, n:n+1])を使って1列の列ベクトルに変換する必要がある。
y: ターゲットの配列で、通常は1変数で1次元配列。

3つ目の引数sample_weightは省略。

適合度の計算

score()メソッドに特徴量とターゲットを与えて適合度を計算する。

lr.score(X, y)

1	lr.score(X, y)

戻り値は適合度を示す実数で、回帰計算の決定係数R²で計算される。

(1) $\begin{equation*} R^2 = 1 - \frac{RSS}{TSS} = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \overline{y})^2} \end{equation*}$

モデルによる予測

predict()メソッドに特徴量を与えて、ターゲットの予測結果を得る。

y_pred = lr.predict(X)

1	y_pred = lr.predict(X)

ここで特徴量Xは複数のデータセットの2次元配列を想定しており、1組のデータの場合でも2次元配列とする必要がある。

y_pred = lr.pred([[x1, x2,..., xm]])

1	y_pred = lr.pred([[x1, x2,..., xm]])

また、結果は複数のデータセットに対する1次元配列で返されるため、ターゲットが1つの場合でも要素数1の1次元配列となる。

切片・係数の利用

fit()メソッドによる学習後、モデルの学習結果として切片と特徴量に対する重み係数を得ることができる。

各々モデル・インスタンスのプロパティーとして保持されており、切片はintercept_で1つの実数、重み係数はcoeff_で特徴量の数と同じ要素数の1次元配列となる(特徴量が1つの場合も要素数1の1次元配列)。

ic = lr.intercept_
cf = lr.coef_

1 2	ic = lr.intercept_ cf = lr.coef_

末尾のアンダースコアに注意。

実行例

waveデータセットに対する単回帰

英語 – 機械学習

2020-05-10 / tau / コメントする

説明変数・独立変数

explately variable, regressor, independent variable, designed variable

被説明変数・従属変数: explained variable, regressand, dependent variable, designed variable

Lasso回帰の理解

2020-05-06 / tau / コメントする

定義

Ridge回帰は単純な多重回帰の損失関数に対してL2正則化項を加え、多重共線性に対する正則化を図った。Lasso解析はこれに対してL1正則化項を加えて最小化する(正則化の意味についてはこちら)。

(1) $\begin{align*} L &= \frac{1}{2} \sum_{i=1}^n ( y_i - \hat{y}_i )^2 + \alpha (|w_1| + \cdots + |w_m|) \\ &= \frac{1}{2} \sum_i ( y_i - w_0 - w_1 x_{1i} - \cdots - w_m x_{mi} )^2 + \alpha (|w_1| + \cdots + |w_m|) \end{align*}$

L1正則化の意味

準備

L2正則化は各重み係数が全体として小さくなるように制約がかかったが、L1正則化では値がゼロとなる重み係数が発生する。このことを確認する。

係数wを求めるためには損失関数Lを最小化すればよいが、Ridge回帰とは異なりL1正則化項は通常の解析的な微分はできない。

(2) $\begin{align*} \frac{\partial L}{\partial w_k} &= - \sum_i x_{ki} ( y_i - w_0 - w_1 x_{1i} - \cdots - w_m x_{mi} ) + \alpha \frac{\partial |w_k|}{\partial w_k} \\ &= - \sum_i x_{ki}y_i + w_0 \sum_i x_{ki} + \sum_{j \ne k} w_j \sum_i x_{ji} x_{ki} + w_k \sum_i {x_{ki}}^2 + \alpha \frac{\partial |w_k|}{\partial w_k} \\ &= 0 \end{align*}$

ここで $\frac{\partial |w_k|}{\partial w_k}=|w_k|'$ と表し、左辺のw_k以外に関わる項をM_k、w_kの係数となっている2乗和をS_kkと表す。

(3) $\begin{equation*} M_k + w_k S_{kk} + \alpha |w_k|' = 0 \end{equation*}$

場合分け

ここで|w_k|’についてはw_kの符号によって以下の値をとる。

(4) $\begin{equation*} |w_k|' = \left\{ \begin{array}{rl} -1 & (w_k < 0) \\ 1 & (w_k > 0) \end{array} \end{equation*}$

これらを式(3)に適用する。まずw_k < 0に対しては

(5) $\begin{gather*} w_k < 0 \quad \rightarrow \quad M_k + w_k S_{kk} - \alpha = 0 \\ -M_k + \alpha < 0 \quad \rightarrow \quad w_k = \frac{-M_k + \alpha}{S_{kk}} \end{gather*}$

またw_k > 0に対しては、

(6) $\begin{gather*} w_k > 0 \quad \rightarrow \quad M_k + w_k S_{kk} + \alpha = 0 \\ -M_k - \alpha > 0 \quad \rightarrow \quad w_k = \frac{-M_k - \alpha}{S_{kk}} \end{gather*}$

以上をまとめると、

(7) $\begin{equation*} w_k = \left\{ \begin{array}{ll} \dfrac{-M_k - \alpha}{S_{kk}} & (M_k < -\alpha) \\ \\ \dfrac{-M_k + \alpha}{S_{kk}} & (M_k > \alpha) \\ \end{array} \right. \end{equation*}$

劣微分の導入

式(7)で−α ≤ M_k ≤ αについては得られていない。M_k → ±αについてそれぞれの側から極限を計算すると0となるのでその間も0でよさそうだが、その保証はない。

ここでこちらのサイトのおかげで”劣微分(subdifferential)”という考え方を知ることができた。|w_k|’についてw_k = 0では解析的に微分不可能だが、その両側から極限をとった微分係数の範囲の集合を微分係数とするという考え方のようだ。

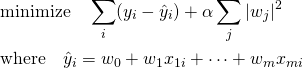
(8) $\begin{equation*} \frac{d |x|}{dx} = \left\{ \begin{array}{cl} -1 & (x < 0) \\ \left[ -1, 1 \right] & (x = 0) \\ 1 & (x > 0) \end{array} \right. \end{equation*}$

そこで、w_k = 0に対してこの劣微分を適用してみる。

(9) $\begin{gather*} w_k = 0 \quad \rightarrow \quad M_k +w_k S_{kk} + \alpha \left[ -1, 1 \right] = \left[ M_k - \alpha , M_k + \alpha \right] = 0\\ M_k - \alpha \le 0 \le M_k + \alpha \quad \rightarrow \quad -\alpha \le M_k \le \alpha \quad \rightarrow \quad w_k = 0 \end{gather*}$

以上のことから、重みw_kについて以下のようになり、−α≤M_k≤αの範囲ではw_k = 0となることがわかる。

(10) $\begin{equation*} w_k = \left\{ \begin{array}{cl} \dfrac{-M_k - \alpha}{S_{kk}} & (M_k < -\alpha \quad)\\ \\ 0 & (-\alpha \le M_k \le \alpha) \\ \\ \dfrac{-M_k + \alpha}{S_{kk}} & (M_k > \alpha) \end{array} \right. \end{equation*}$

すなわちL1正則化の場合、ハイパーパラメータαは重み係数の大きさを制限すると同時に重み係数がゼロとなるような効果も持ち、αが大きいほど多くの重み係数がゼロとなりやすい。

参考サイト

本記事をまとめるにあたって、下記サイトが大変参考になったことに感謝したい。

Lassoを数式から実装まで(理論編)～Miidas Research

概要

得られるデータの形式

利用例

パラメーターの指定

モデルの精度

学習精度の向上

特徴量の係数

L2正則化の場合

L1正則化の場合

係数の符号と選択確率について

概要

利用例

利用方法

モデルクラスのインポート

モデルのインスタンスの生成

モデルの学習

適合度の計算

その他のメソッド

概要

決定境界

3次元表示

概要

Ridge回帰

Lasso回帰

Ridge回帰とLasso回帰の挙動

係数の大きさ

学習曲線

概要

データの取得とデータ構造

データの内容

'data'～特徴量データセット

'target'～糖尿病の進行度

'feature_names'～特徴名

'filename'～ファイル名

diabetes_data.csv

diabetes_target.csv

‘DESCR’～データセットの説明

データの利用

各データの取得方法

dataの扱い

概要

データ数が少ない場合

異常値がある場合

データ数を多くした場合

概要

利用例

配列による場合

DataFrameによる場合

利用方法

モデルクラスのインポート

モデルのインスタンスの生成

モデルの学習

適合度の計算

モデルによる予測

切片・係数の利用

実行例

定義

L1正則化の意味

準備

場合分け

劣微分の導入

参考サイト

`'data'`～特徴量データセット

`'target'`～糖尿病の進行度

`'feature_names'`～特徴名

`'filename'`～ファイル名