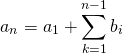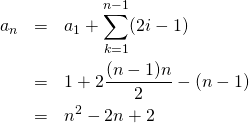カテゴリー: 科学・工学

ヒストグラムと確率密度曲線を重ねて描くとき

/ tau / コメントする

概要

ある確率分布に従っていると思われるデータのヒストグラムと、その確率分布の確率密度曲線を重ねて描きたい場合がある。

RやPythonのmatplotlibではヒストグラムを描く機能が提供されていて、縦軸に度数をとったり、頻度(確率)をとったり選択できる。

縦軸に頻度を選んだ場合は、そのまま確率密度の曲線を重ねて描けばよいが、度数の場合に確率密度を重ねる手順でちょっと戸惑ったので、その手順を記録。

一様分布の例

例として、0 ≤ x <1の値が一様な確率で現れる確率分布を考える。その確率密度曲線は以下のようになる。

histogram_and_probability_density_1

(1)   \begin{equation*} \int_0^\infty u(x) dx = \int_0^\infty 1 dx = \left[ x \right]_0^\infty = 1 \end{equation*}

この一様乱数を1000個発生させて、その度数をヒストグラムに表した場合を考える。

仮に各値が実際に全く一様に表れたとすると、グラフは以下のようになり、階級幅によって高さの値が変わってくる。

histogram_and_probability_density_2

ヒストグラムの定義を、「ある階級に含まれる度数が階級幅と高さの積」と定義すれば、上の縦軸の値は1000となり、階級幅を変えても高さは変わらないが、縦軸の値を度数とすることで、階級幅によって縦軸の値が変化することになってしまう。

一般論

次に、一般の確率密度関数を考える。

histogram_and_probability_density_3

確率密度関数をf(x)として、区間[x, x + dx)の間の確率P(x)は次式のようになる。

(2)   \begin{equation*} P(x) = f(x) dx \end{equation*}

両辺に全度数Nをかけると、その値は値xの階級におけるヒストグラムの高さに相当する。

(3)   \begin{equation*} N P(x) = N f(x) dx \end{equation*}

階級iの高さをhi、階級幅をwiとすると、次式は以下のように書ける。

(4)   \begin{equation*} h_i = N w_i f(x) \end{equation*}

したがって、縦軸が度数表示のヒストグラムに確率密度曲線を重ねて描く場合、階級幅wが一定なら、確率密度関数に総度数Nと階級幅wを乗じて描けばよい。

 

待ち行列(M/M/1)の再現 – イベント制御

/ tau / コメントする

考え方

M/M1待ち行列のシミュレーションを、イベント制御(event driven)で行う。M/M/1待ち行列の解析的アプローチはこちら。言語はRを使う。なお時刻制御によるケースはこちら。

計算手順のブロックは次の3つ。

  1. 全てのトランザクションの到着時刻を指数分布に従って発生させる
  2. 時刻0から指数分布に従ってサービス時間を1つずつ発生させる
    1. 待ち状態のトランザクションがあればすぐに次のサービスを開始
    2. 待ち状態のトランザクションがなければ、次のトランザクション到着時にサービス開始
  3. 待ち行列長の推移を集計し、結果を表示する

定数定義

トランザクションの到着時刻の発生

到着時間間隔を乱数で発生させてトランザクションの到着時刻を発生させる。手順についてはイベント制御によるポアソン過程のシミュレーションを参照。

サービス時間の計算

下図に考え方を示す。

queue-mm1-event-driven-fig1

  1. 時刻0でトランザクション1到着
  2. 時刻0でサービス1開始
  3. 指数乱数でサービス1の終了時刻を計算
  4. 終了時刻より前に次のトランザクション2が到着している
  5. すぐにトランザクション2に対してサービス2を開始
  6. サービス2の終了時刻を指数乱数で計算
  7. 終了時刻より前に次のトランザクション3が到着している
  8. すぐにトランザクション3に対してサービス3を開始
  9. サービス3の終了時刻を指数乱数で計算
  10. 次のトランザクション4の到着は終了時刻より後
  11. トランザクション4の到着と同時にサービス4を開始する
  12. サービス4の終了時刻を指数乱数で計算

待ち行列長の推移の集計

以下の手順によっている。

  1. トランザクションの到着時とサービス終了時の時刻を取り出し、時刻と増減値をデータフレームにまとめる
  2. 時刻順にソート
  3. 待ち行列長の推移を計算する

ここで、トランザクション数と待ち行列長には、到着したトランザクション自身はカウントしていない(長さ0も考慮するため)。

計算結果の表示

待ち行列時系列データの真ん中1/3を取り出し、トランザクション到着時のトランザクション数、待ち行列長を集計している。比較のため、それらの理論値も計算・表示している。

計算結果

1000個のデータからトランザクション数、待ち行列長を10回計算させ、それらについて割り戻したλの逆数、各データの平均と標準偏差を計算した。

ρ = 0.5のケース

λ = 1/10、μ = 1/5、ρ = 0.5のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 1、Lq = 0.5で、これらに対する待ち時間はT = 10、Tw = 5。

トランザクション数に関する計算結果は、かなり理論値と整合している。

L T 1/λ
1 0.977022977 9.767519297 9.997225783
2 1.181818182 12.00225815 10.1557569
3 1.236763237 11.35299611 9.17960348
4 0.87012987 9.097838003 10.45572427
5 0.943056943 9.652253196 10.23506933
6 1.132867133 11.09199315 9.791080377
7 0.958041958 9.28812046 9.694899459
8 1.347652348 12.61173676 9.358301328
9 1.058941059 10.13796162 9.573678846
10 0.867132867 9.19585645 10.60489897
AVG 1.057342657 10.41985332 9.854755454
STD 0.162710928 1.258385656 0.467315969

待ち行列についても、整合性は良い。

Lq Tq 1/λ
1 0.460539461 4.687171936 10.17756856
2 0.632367632 6.669065267 10.54618378
3 0.686313686 6.311337813 9.195995853
4 0.391608392 4.163816097 10.63260182
5 0.471528472 4.72111758 10.01237012
6 0.634365634 6.030695282 9.506655083
7 0.465534466 4.447464396 9.553458927
8 0.785214785 7.437052562 9.471360832
9 0.564435564 5.262195935 9.322934744
10 0.367632368 4.099711426 11.1516607
AVG 0.545954046 5.382962829 9.859736125
STD 0.136420649 1.159489377 0.655334793

ρ = 0.9のケース

λ = 1/10、μ = 1/9、ρ = 0.9のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 9、Lq = 8.1で、これらに対する待ち時間はT = 90、Tw = 81。

トランザクション数に関する計算結果は、理論値よりも大きく出ている。

L T 1/λ
1 10.11288711 100.5733569 9.945068678
2 12.03096903 120.0280761 9.97659256
3 15.71128871 162.6168804 10.35032093
4 10.998002 110.2958229 10.02871457
5 18.26373626 178.496846 9.773293013
6 7.716283716 77.4353613 10.03531806
7 6.178821179 62.23838321 10.07285717
8 9.491508492 95.64553268 10.07695803
9 6.951048951 70.34023525 10.11936986
10 6.073926074 63.43794238 10.44430597
AVG 10.35284715 104.1108437 10.05625237
STD 4.076793696 40.26529308 0.192915047

待ち行列長についても傾向は同じ。

Lq Tq 1/λ
1 9.204795205 91.66512812 9.95841038
2 11.13286713 110.9692603 9.967716221
3 14.76723277 152.9773707 10.35924422
4 10.07392607 101.1184062 10.03763631
5 17.28271728 169.1669214 9.7882132
6 6.789210789 68.44424425 10.08132556
7 5.254745255 53.24239678 10.13225079
8 8.545454545 86.43775829 10.11505682
9 6.06993007 61.37562417 10.11142195
10 5.220779221 54.59901247 10.4580198
AVG 9.434165834 94.99961227 10.06974161
STD 4.051237304 40.07040651 0.193152208

稼働率をρが1に近づくと、計算結果に乖離がみられる。たとえばN = 10000個のデータについて計算してみても、傾向は変わらない。

 

 

待ち行列(M/M/1)

/ tau / コメントする

前提

時刻t～t + Δtの間に以下のいずれかの状態遷移が発生するとする。希少性の仮定から、2つ以上の事象が同時に起こることはなく、いずれか1つが発生するとする。

  • 確率λΔtで1つのトランザクションが到着する
  • 確率μΔtで1つのサービスが完了する
  • 確率(1 – λΔt – μΔt)でトランザクションの到着もなくサービスも完了しない
    • 本来は(1 – λΔt)(1  – μΔt)で表されるところ、これを展開してΔt2の項を無視してこの形になる
    • あるいは指数分布の密度関数をMaclaurin展開して2時以上の項をo(Δt2)として消していってもよい

なお、M/M/1待ち行列のイベント制御による再現をR言語で試している。

状態方程式

システムの状態を、システム内のトランザクション数nで表す。nには、サービスを受けているトランザクションとサービスを待機しているトランザクションの数の和。

時刻tにおいてトランザクション数がnである状態確率をpn(t)とすると、状態方程式は以下のようになる。

(1)   \begin{eqnarray*} p_n (t + \Delta t) &=& p_{n-1} \lambda \Delta t + p_n (t) (1 - \lambda \Delta t - \mu \Delta t) + p_{n+1} \mu \Delta t \\ p_{0}(t + \Delta t) &=& p_{0}(1 - \lambda \Delta t) + p_{1} \mu \Delta t \end{eqnarray*}

まず式(1)の第1式について、

(2)   \begin{eqnarray*} \frac{dp_n (t)}{dt} &=& \lim_{\Delta t \rightarrow 0} \frac{p_n(t + \Delta t) - p_n (t)}{\Delta t} \\ &=& p_{n-1} \lambda - p_n (\lambda + \mu) + p_{n+1} \mu \end{eqnarray*}

また第2式については、

(3)   \begin{eqnarray*} \frac{dp_0 (t)}{dt} &=& \lim_{\Delta t \rightarrow 0} \frac{p_0(t + \Delta t) - p_0 (t)}{\Delta t} \\ &=& - p_0 \lambda + p_1 \mu \end{eqnarray*}

式(2)と式(3)を改めてまとめて書くと、

(4)   \begin{eqnarray*} \frac{dp_n (t)}{dt} &=& \lambda p_{n-1} - (\lambda + \mu) p_n + \mu p_{n+1} \\ \frac{dp_0 (t)}{dt} &=& - \lambda p_0 + \mu p_1 \end{eqnarray*}

定常問題化と状態方程式の解

状態方程式においてt → ∞でトランザクション数の変化がなく一定値に収束するとして、次式を得る。

(5)   \begin{eqnarray*} \lambda p_{n-1} - (\lambda + \mu) p_n + \mu p_{n+1} &=& 0 \quad (n > 0) \\ - \lambda p_0 + \mu p_1 &=& 0 \end{eqnarray*}

ここでρ = λ/μ < 0とおいて、

(6)   \begin{eqnarray*} \rho p_{n-1} - (1 + \rho) p_n + p_{n+1} &=& 0 \quad (n > 0) \\ - \rho p_0 + p_1 &=& 0 \end{eqnarray*}

これは階差数列の式に変形できて、

(7)   \begin{eqnarray*} p_n - p_{n-1} &=& \rho (p_n - p_{n-1}) \\ p_1 &=& \rho p_0 \end{eqnarray*}

上式から順次各項を求めると、

(8)   \begin{eqnarray*} p_1 &=& \rho p_0 \\ p_2 &=& \rho (p_1 - p_0) + p_1 = \rho p_1 = \rho ^2 p_0 \\ p_3 &=& \rho(p_2 - p_1) + p_2 = \rho p_2 = \rho ^3 p_0 \\ &\cdots& \\ p_n &=& \rho ^n p_0 \end{eqnarray*}

全事象の和が1という条件から、以下の結果を得る。

(9)   \begin{eqnarray*} \sum_{i=0}^\infty p_n &=& p_0 (1 + \rho + \rho ^2 + \cdots ) = p_0 \frac{1}{1 - \rho} = 1 \\ \therefore \quad p_0 &=& 1 - \rho \end{eqnarray*}

これより、システムの状態がnである確率は以下で表せる。

(10)   \begin{equation*} p _n &=& (1 - \rho) \rho ^n \end{equation*}

ρの意味

ρ = λ / μは、単位時間当たりのサービス提供数に対する単位時間当たりのトラフィック到達数で、サービスの混み具合を表している。また、どの程度サービスが稼働しているか／利用されているか、とも言えるので、混雑度、平均稼働率／利用率、平均到達率、平均トラフィック密度などと呼ばれている。

平均トランザクション数と平均待ち行列長

システム内の平均トランザクション数Lは、

(11)   \begin{eqnarray*} L &=& \sum_{n=0}^\infty n p_n = (1 - \rho) \sum_{n=0}^\infty n \rho ^n \\ &=& (1 - \rho) \left(0 \cdot \rho^0 + 1 \cdot \rho^1 + 2 \cdot \rho^2 + \cdots \right) \end{eqnarray*}

これを以下のように解く。

(12)   \begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} \displaystyle \frac{1}{1 - \rho} L_n &= &1 \cdot \rho ^1 &+ &2 \cdot \rho ^2 &+ &\cdots &+ &\n \rho^n \\ \displaystyle \frac{\rho}{1 - \rho} L_n &= & & &1 \cdot \rho^2 &+ &\cdots &+ &(n - 1) \rho^n &+ &n \rho^{n + 1} \\ \hline L_n &= &\rho &+ &\rho^2 &+ &\cdots &+ &\rho^n &- &n \rho^{n+1} \end{array} \\ \\ & &L_n = \rho \frac{1 - \rho^n}{1 - \rho} - n \rho^{n+1} \end{eqnarray*}

よって、

(13)   \begin{equation*} L = \lim_{n \rightarrow \infty} L_n = \frac{\rho}{1 - \rho} \end{equation*}

また平均待ち行列長については、サービス中のトランザクションを除いて考えて、

(14)   \begin{eqnarray*} L_q &=& 0 \cdot p_0 + 0 \cdot p_1 + 1 \cdot p_2 + 2 \cdot p_3 + \cdots\\ &=& (1 - \rho) \left( 1 \cdot \rho^2 + 2 \cdot \rho^3 + \cdots \right) \end{eqnarray*}

これも以下のように解く。

(15)   \begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} \displaystyle \frac{1}{1 - \rho} L_qn &= &1 \cdot \rho ^2 &+ &2 \cdot \rho ^3 &+ &\cdots &+ &\n \rho^{n+1} \\ \displaystyle \frac{\rho}{1 - \rho} L_qn &= & & &1 \cdot \rho^3 &+ &\cdots &+ &(n - 1) \rho^{n + 1} &+ &n \rho^{n + 2} \\ \hline L_n &= &\rho^2 &+ &\rho^3 &+ &\cdots &+ &\rho^{n+1} &- &n \rho^{n+2} \end{array} \\ \\ & &L_n = \rho^2 \frac{1 - \rho^n}{1 - \rho} - n \rho^{n+2} \end{eqnarray*}

よって、

(16)   \begin{equation*} L_q = \lim_{n \rightarrow \infty} L_qn = \frac{\rho^2}{1 - \rho} \end{equation*}

リトルの法則(Litter’s law)

定常状態にある待ち行列において、トランザクションがシステムに到着してからサービスを終えるまでの時間の平均(平均応答時間)をTとすると、その間に平均してλTのトランザクションが到着することから、次式が成り立つ。

(17)   \begin{equation*} L = \lambda T \end{equation*}

また、同じことが待ち行列長Lqと平均待ち時間Tqにも言えるので、

(18)   \begin{equation*} L_q = \lambda T_q \end{equation*}

リトルの公式を使うと、待ち行列の長さと到着率から、平均待ち時間が計算できる。

(19)   \begin{eqnarray*} T &=& \frac{L}{\lambda} \\ T_q &=& \frac{L_q}{\lambda} \end{eqnarray*}

たとえば客の列に到着したときの行列の人数を数え、その後到着する客の数や出ていく客の数から到着率を推定することで、待ち時間を推定できる。

 

R – データフレームのソート

/ tau / 2件のコメント

order()関数

以下のデータを準備する。

このデータフレームをheightの項目の昇順のオーダーでソートしたいとする。

order()関数というのがあって、引数の項目でソートしたときに元データの項目番号がどういう順番で並ぶかを返してくれる。

たとえば1番目のデータは1番小さい157で、これは5番目のデータ。2番目のデータは2番目に小さい160で2番目のデータ・・・という風に、heightデータを昇順に並べた時の元データの項目番号の並びを教えてくれる。

rank()関数がデータを昇順に並べた時の、そのデータのソート後の順番を返すのとは違う点に注意。

この結果を元のデータフレームの行部分に使うと、その順番で並べ替えられたデータを返してくれる。

降順ソート

データを降順にソートしたい時は、decreasing=Tで指示する。

複数列のソートなど

以下の例は、数値以外でもソートできることと、複数のオーダーを組み合わせたソートの例を示している。

行番号の変更

ソート後に行ラベルを振り直したい場合は、rownames()の内容を変更する。

 

 

数列の和と階差数列

/ tau / コメントする

定数数列

定数数列の和は、定数の項数倍。

(1)   \begin{equation*} \sum_{k=1}^{n} a = an \end{equation*}

等差数列

等差数列a_n = a + d(n - 1)の和は、初項と末項の和に項数を乗じた数の1/2。

(2)   \begin{equation*} \sum_{k=1}^{n} (a + d(k-1)) = \frac{1}{2}n(a_1 + a_n) \end{equation*}

特に、

(3)   \begin{equation*} \sum_{k=1}^{n} k = \frac{n (n + 1)}{2} \end{equation*}

証明1

等差数列のn項目までの和をS_nとすると、

(4)   \begin{eqnarray*} & & \begin{array}{rcccccccc} S_n &= &a_1 &+ &(a_1 + d) &+ &\cdots & + &a_n \\ S_n &= &a_n &+ &(a_n - d) &+ &\cdots &+ &a_1 \\ \hline 2 S_n &= &(a_1 + a_n) &+ &(a_1 + a_n) &+ &\cdots &+ &(a_1 + a_n) } \end{array} \\ \\ & & \therefore \quad S_n = \frac{1}{2} n (a_1 + a_n) \end{eqnarray*}

証明2

式(3)を使って、

(5)   \begin{eqnarray*} \sum_{k=1}^n (a + d(k - 1)) &=& an + d \frac{n (n + 1)}{2} - dn \\ &=& \frac{1}{2} n (2a + dn + d - 2d) \\ &=& \frac{1}{2} n (a + a + d(n-1)) \\ &=& \frac{1}{2} n (a_1 + a_n) \end{eqnarray*}

等比数列

等比数列a_n = a r^{n-1}の和は以下の通り。

(6)   \begin{equation*} \sum_{k=1}^n a r^{k-1} = a \frac{1 - r^n}{1 - r} \end{equation*}

特に、

(7)   \begin{equation*} \sum_{k=1}^{n} r^k = r \frac{1 - r^n}{1 - r} \end{equation*}

証明

等差数列のn項目までの和をS_nとすると、

(8)   \begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} S_n& = &a &+ &a r &+ &\cdots &+ &a r^{n-1} \\ r S_n &= & & &a r &+ &\cdots &+ &a r^{n-1} &+ &a r^n \\ \hline (1 - r) S_n &= &a & & & & & & &- &a r^n \\ \end{array} \\ \\ & & \therefore \quad S_n = a \frac{1 - r^n}{1 - r} \end{eqnarray*}

等比・等差の複合数列

等差部分と等比部分の両方を含んだ数列の部分和。

(9)   \begin{equation*} \sum_{k=1}^{n} k r^k = r \frac{1 - (n + 1) r^n + n r^{n + 1}}{(1 - r)^2} \end{equation*}

証明1

一般的な部分和の差を用いる方法。

(10)   \begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} S_n& = &1 \cdot r^1 &+ &2 \cdot r^2 &+ &\cdots &+ &n r^n \\ r S_n &= & & &1 \cdot r^2 &+ &\cdots &+ &(n - 1) r^n &+ &n r^{n + 1} \\ \hline (1 - r) S_n &= &r &+ &r^2 &+ &\cdots &+ &r^n &- &n r^{n+1} \end{array} \\ \\ & &(1 - r) S_n = r \frac{1 - r^n}{1 - r} - n r^{n+1}\\ & & \therefore \quad S_n = r \frac{1 - r^n}{(1 - r)^2} - n \frac{r^{n+1}}{1 - r} = r \frac{1 - (n + 1) r^n + n r^{n + 1}}{(1 - r)^2} \end{eqnarray*}

証明2

微分を用いる方法。等比数列の公式、

(11)   \begin{equation*} \sum_{k=1}^n r^k = \frac{r (1 - r^n)}{1 - r} \end{equation*}

の両辺をrで微分すると、

(12)   \begin{eqnarray*} \sum_{k=1}^n k r^{k - 1} &=& \frac{(1 - r)(1 - (n + 1) r^n) + r(1 - r^n)}{(1 - r)^2} \\ &=& \frac{1 - (n+1) r^n + n r^{n+1}}{(1 - r)^2} \end{eqnarray*}

両辺をr倍して同じ式を得る。

べき乗の数列

∑k2

(13)   \begin{equation*} \sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6} \end{equation*}

証明

以下の式から出発する。

(14)   \begin{eqnarray*} \sum_{k=1}^{n} \left( (k + 1)^3 - k^3 \right) &=& (n+1)^3 - 1 \\ \sum_{k=1}^{n} \left( (k + 1)^3 - k^3 \right) &=& \sum_{k=1}^{n} (3k^2 + 3k + 1) \end{eqnarray*}

これより、

(15)   \begin{eqnarray*} \sum_{k=1}^{n} k^2 &=& \frac{(n+1)^3 - 1}{3} - \frac{n(n+1)}{2} - \frac{n}{3} \\ &=& \frac{2n^3 + 6n^2 + 6n - 3n^2 - 3n - 2n}{6} \\ &=& \frac{n(2n^2 + 3n +1)}{6} \\ &=& \frac{n(n+1)(2n+1)}{6} \end{eqnarray*}

∑k3

(16)   \begin{equation*} \sum_{k=1}^{n} k^3 = \frac{n^2 (n+1)^2}{4} \end{equation*}

証明

上記と同じように、

(17)   \begin{eqnarray*} \sum_{k=1}^{n} \left( (k + 1)^4 - k^4 \right) &=& (n+1)^4 - 1 \\ \sum_{k=1}^{n} \left( (k + 1)^4 - k^4 \right) &=& \sum_{k=1}^{n} (4k^3 + 6k^2 + 4k + 1) \end{eqnarray*}

これより、

(18)   \begin{eqnarray*} \sum_{k=1}^{n} k^3 &=& \frac{(n+1)^4 - 1}{4} - \frac{6}{4} \cdot \frac{n(n+1)(2n+1)}{6} -\frac{n(n+1)}{2} - \frac{n}{4} \\ &=& \frac{n^4 + 4n^3 + 6n^2 + 4n - 2n^3 - 3n^2 - n - 2n^2 - 2n - n}{4} \\ &=& \frac{n^4 + 2n^3 + n^2}{4} \\ &=& \frac{n^2 (n+1)^2}{4} \\ \end{eqnarray*}

階差数列

数列a_nの階差数列が扱いやすい数列の場合。

(19)   \begin{equation*} a_{n+1} - a_n = b_n \end{equation*}

a_nの各項は、a_1]～a_nの和をとることで以下のように得られる。

(20)   \begin{equation*} a_n = a_1 + \sum_{k=1}^{n-1} b_i \end{equation*}

【例】

a_nの階差数列がa_n - a_{n-1} = 2n - 1でa_1 = 1のときの数列a_nは以下のようになる

    \begin{equation*} 1 \underbrace{\quad}_{1} 2 \underbrace{\quad}_{3} 5 \underbrace{\quad}_{5} 10 \cdots \end{equation*}

この数列の一般項は、

(21)   \begin{eqnarray*} a_n &=& a_1 + \sum_{k=1}^{n-1} (2i - 1) \\ &=& 1 + 2 \frac{(n - 1) n}{2} - (n - 1) \\ &=& n^2 - 2n + 2 \end{eqnarray*}

上式はn = 1の時も初期条件a_1 = 1を満足する。

 

イベント制御によるポアソン過程のシミュレーション

/ tau / コメントする

イベント制御による分析

時刻制御(time driven)では微小な時間間隔の間において到着イベントを確率的に発生させた。そこでは結果としての到着時間間隔の指数分布や到着数のPoisson分布は前提にはおかれていない。

イベント制御(event driven)の考え方では、ある到着があった後、次の到着までの時間間隔を指数分布に従う乱数を発生させて計算する。計算にはR言語を使う。

イベント制御の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。

到着イベントの時系列

ここでは、到着率はこれまでと同じλ = 1/10として、時刻t = 0からt ≤ 1000秒の間、到着の時間間隔が確率密度e^{- \lambda t}の指数分布に従うような乱数を発生させていく。

指数分布に従う乱数を生成するには逆関数法を使う。

指数分布の確率分布関数は以下の通り。

(1)   \begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}

一様乱数runifを与えて指数分布に従う乱数を得るには、一様乱数を分布関数の逆関数に適用すればよい。

(2)   \begin{equation*} F^{-1}(t) = - \frac{1}{\lambda}\ ln(1 - {\rm runif(1)}) \end{equation*}

時刻0を起点として、1番目の到着時刻をこの指数乱数で決定し、その次の到着時刻も指数乱数で・・・と繰り返して、時刻が上限を超えるまで時系列として記録する。

一様乱数による場合と同じく、到着率1/10、観測時間5000秒として、階級幅100秒、500秒の場合の時系列を生成したのが下図。階級あたりのデータ数と分布の平滑さの関係は、一様乱数による場合やtime drivenの場合と同じ。

poisson-process-event-driven-arrival100

poisson-process-event-driven-arrival500

到着数の分布

到着数の確率分布は、一様乱数による場合やtime drivenと同じように集計する。

結果は、Poisson分布の理論式ともよくあっている。

poisson-process-event-driven-poisson

関連リンク

 

一様乱数によるポアソン過程のシミュレーション

/ tau / コメントする

一様乱数に基づく分析

R言語を使って、到着率をλ、観測時間をtとしてその間の到着時刻を一様乱数で発生させ、それらの分布や到着時間間隔、到着回数の分布などを確認する。

 到着時刻の分布

以下の手順で到着時刻の乱数データを得てヒストグラムを描き、結果の一様性を確認する。

一様分布による到着確率の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。

  • 観測時間tの間の平均到着数はλt
  • ただしtの間で個数を指定して一様乱数を発生させると、全体の到着数を縛ることになる
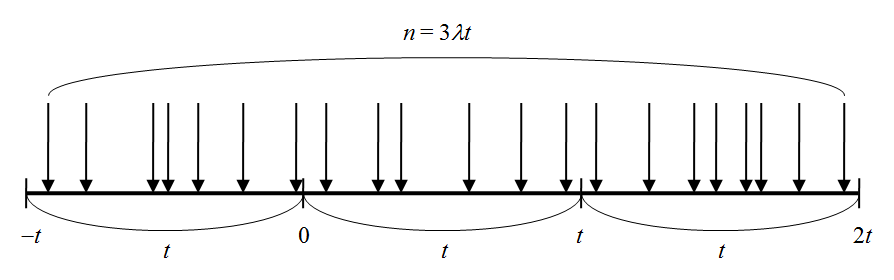
  • そこでtと同じ長さの余裕分をtの前後にとり、区間[–t, 2t)の間で3λt個の乱数を発生させる(到着時間の確率変数)
  • そのデータから、区間[0, t)の範囲にあるデータを抽出し、ヒストグラムを描く
  • その際、データの階級のレンジ～1レンジ幅の平均到着数も変化させてみる

到着率λ = 1/10[回/秒]、観測時間5000[秒]、階級レンジ100秒としたときの、Rのコードは以下の通り。このとき各階級の平均的な到着回数は1/10 * 100 = 10回程度と予想される。

各変数の意味は、

lambda 到着率λ
t.obs 観測時間t
rank.width ヒストグラムの階級幅(時刻幅)。この幅の中の平均到着数はλ*rank_width回。
org.data 前後に余裕幅を持たせた元データ
data t.obsの範囲内だけを切り出したデータ

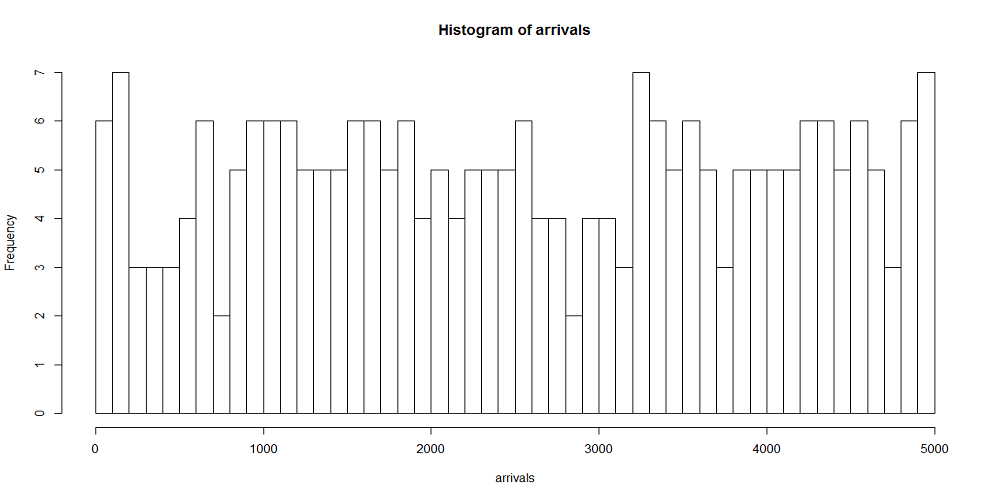
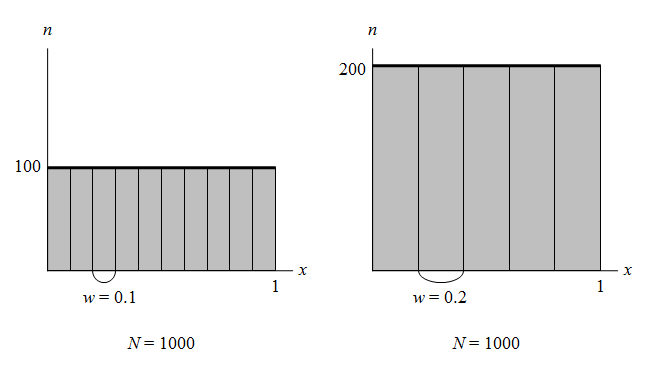
まず、rank.width = 100すなわち時刻幅あたりの平均到着数が10回の場合の分布をみてみる。

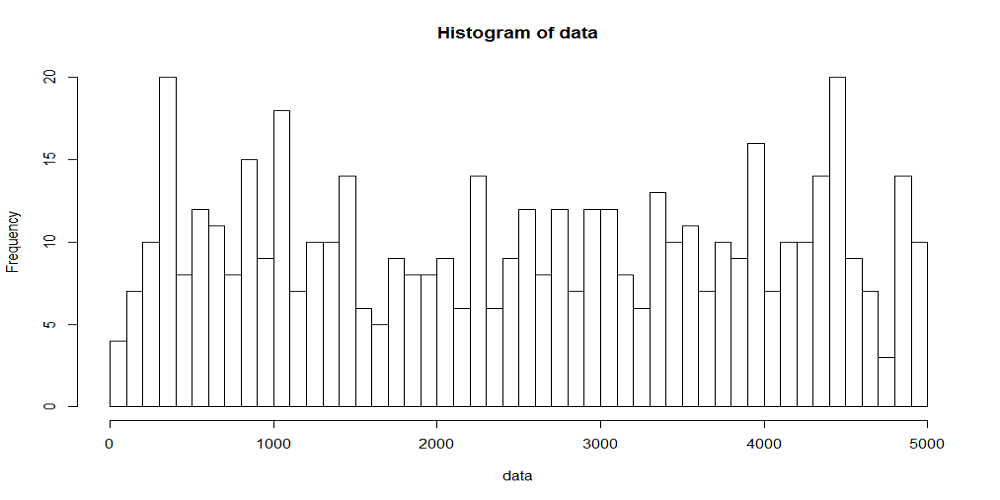
poisson-process-uniform-dist-n010

各時刻幅で到着数が変動していて、平均10回の到着が想定されるところに3～20回とばらついている。

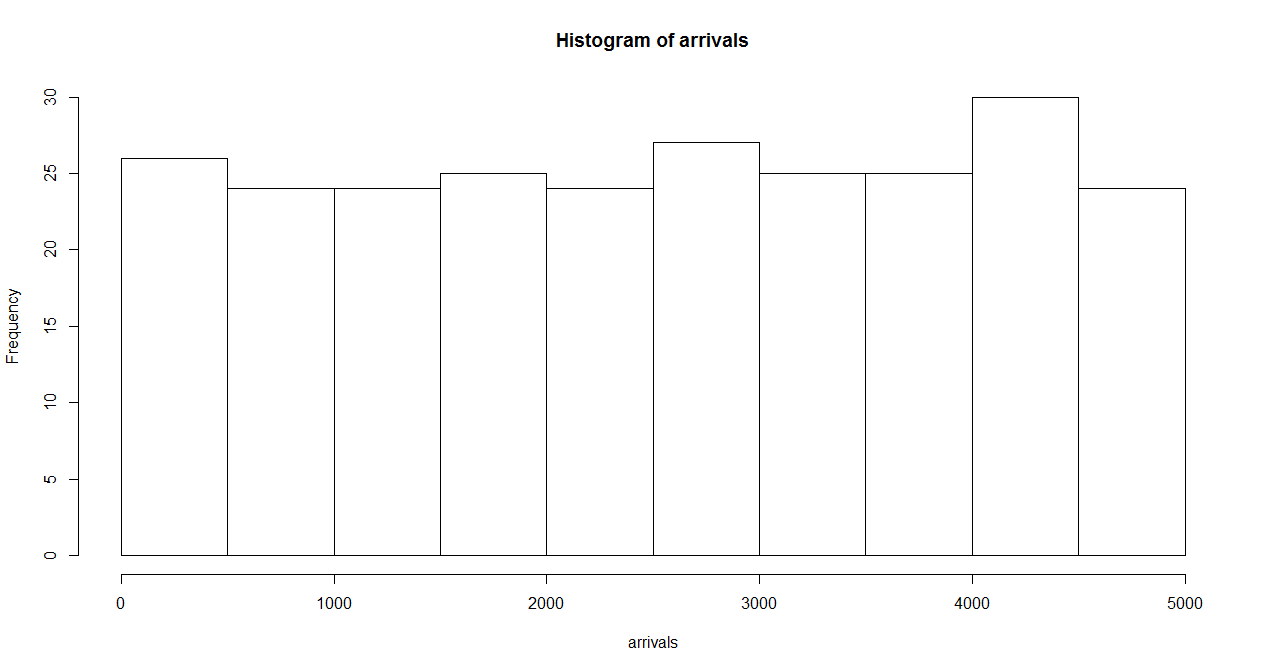
次にrank.width = 500すなわち時刻幅あたりの平均到着数が50回の場合の分布をみてみると、今度は随分と各時刻幅での到着回数が揃ってきているのが確認できる。

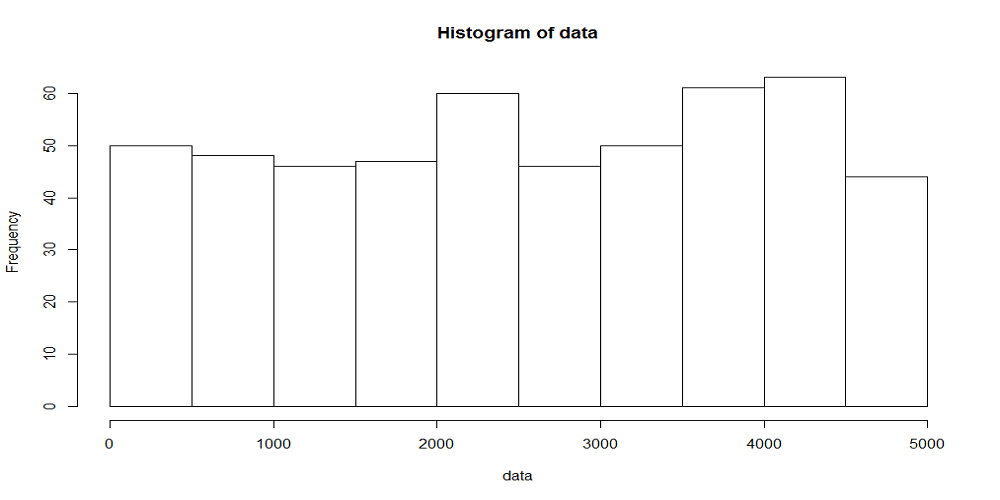
poisson-process-uniform-dist-n050

到着時間間隔の分布

到着時間間隔は、時系列上としてソートされた到着データてn番目の要素からn – 1番目の要素を引いて得られる。この計算は、到着データの先頭を除いたベクトルから最後尾のデータを除いたベクトルを引いて行っている。

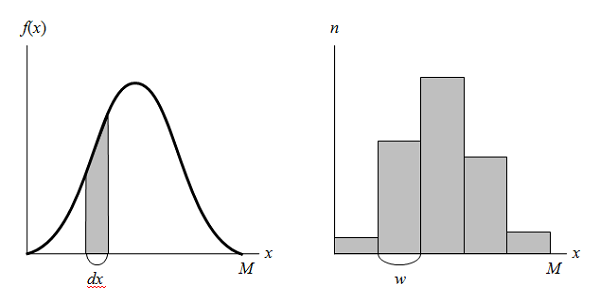
設定条件は到着率λ = 1/10[回/秒。観測時間は分布形には影響を与えず、データ数にのみ関係する。今回はt = 1000秒で、データ数はλt – 1 = 99個。

また、理論上の指数分布の密度関数の曲線をヒストグラムに重ね合わせている。

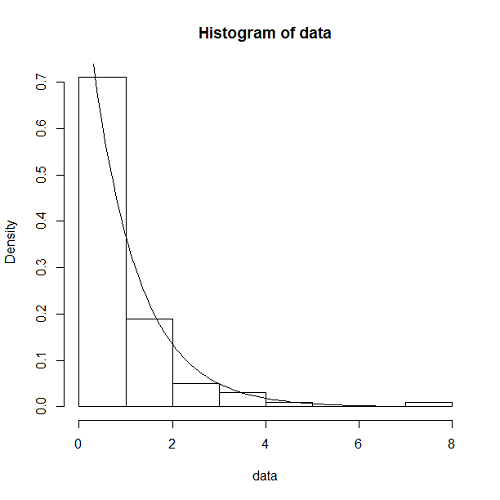
この表示結果は以下のようになる。データ数は99だが、比較的よく指数分布の密度関数と整合している。

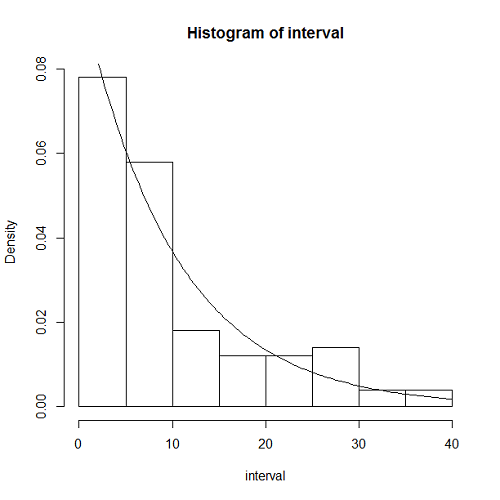
poisson-process-uniform-dist-interval100

到着数の分布

以下の手順で観測時間tの間の到着数のデータを用意する。

  • 必要回数分、以下を繰り返す
    • 観測時間をtとして、区間[–t, 2t)で乱数を発生
    • 0以上、t未満のデータを除いたデータを得てソート
    • その個数を数える

Rのコードは以下の通り。到着率はこれまでと同じ1/10、観測時間は100秒で、この観測時間内の期待到着数は10回だが、これがどの程度ばらつくかを確認するため、このデータを1000回発生させて、ヒストグラムを描かせている。

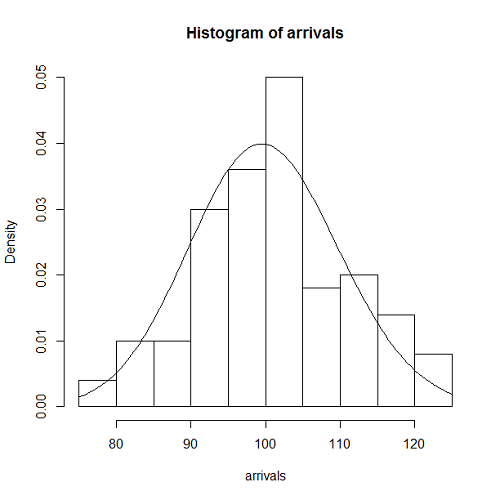
到着率、観測時間が同じパラメータのPoisson分布もあわせて描いたのが以下のグラフ。

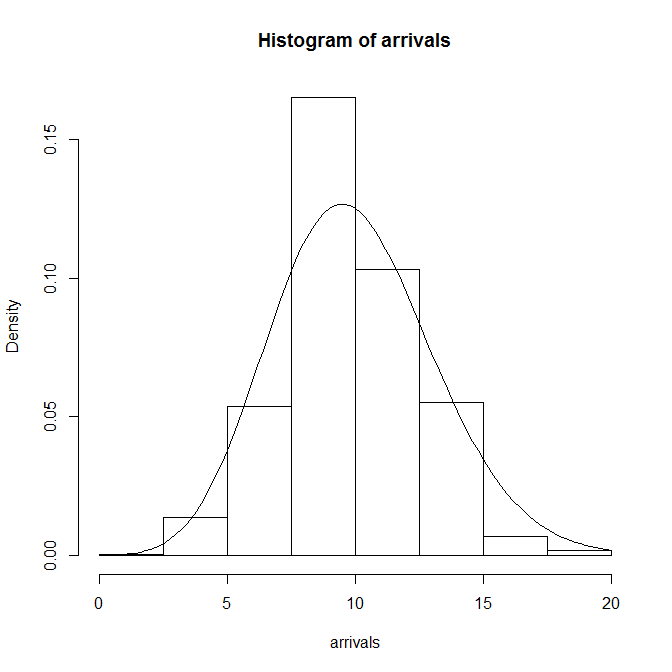
poisson-process-uniform-dist-poisson-n010

到着率を変えずに観測時間tを100→1000秒にした場合の分布は以下のようになる。

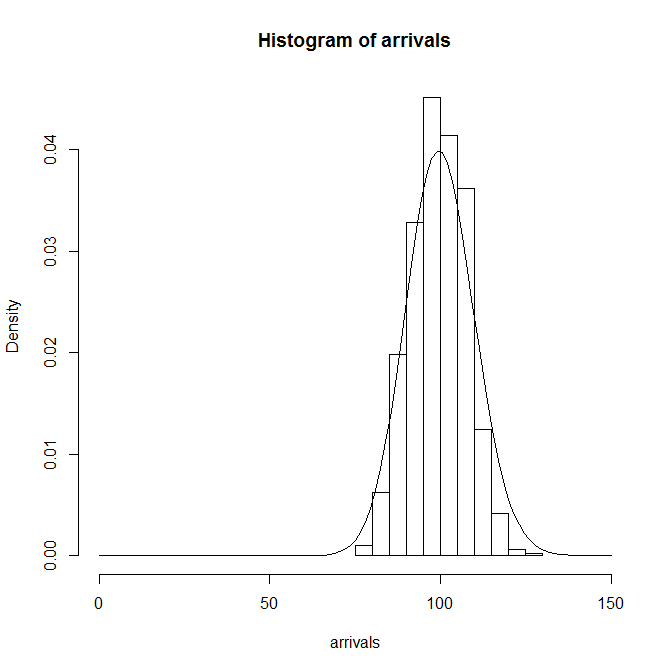
poisson-process-uniform-dist-poisson-n100

ここで縦軸に注意。頻度／確率のスケールが初めのものより小さくなっている。つまり、このグラフは最初のグラフに比べて、右の方へずれて、高さはぐっと低くなっている(この傾向はPoisson分布の傾向)。

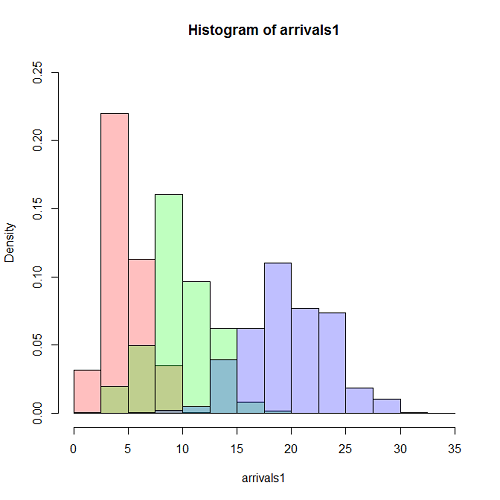
以下に、パラメータλtのtをj変化させたときのヒストグラムを重ね合わせてみる。

poisson-process-uniform-dist-poisson-3params

関連リンク

 

Rによるポアソン過程のシミュレーション

/ tau / コメントする

概要

一様乱数を基にしたポアソン過程のシミュレーションは前にまとめたが、その時には表計算ソフトを使ったので操作性も悪く、限られたケースのみ計算したレベルだった。

その後、統計分析用のソフト”R“を少し勉強したので、より掘り下げた確認をしてみる。

前提条件と手法

平均すると10秒に1回、客が訪れる事象を考える。単位時間を1秒とすると、到着率は\lambda = 1/10となる。この条件下で、以下のことを確認する。

  1. 一様乱数によったときの確率分布
    • 時系列上での到着時刻の分布～一様分布
    • 到着時間間隔の分布～指数分布
    • 到着数の分布～Poisson分布
  2. 時刻制御(time driven)によったときの各種確率分布
    • 同上
  3. イベント制御(event driven)ときの各種確率分布
    • 時系列上での到着時刻の分布～一様乱数
    • 到着数の分布～Poisson分布

考え方

一様乱数による方法

下図のように、観測時間tの間で一度に一様乱数を発生させ、それを昇順にソートしたものを到着時刻の時系列データとする。

poisson-process-fig-uniform-dist

単に到着率λと観測時間tを掛けた平均到着数で乱数を発生させた場合、観測時間内の到着数が一定となってしまうため、観測時間と同じ時間幅で前後に余裕をとり、その中で一様乱数を発生させたうえで両端を切り落としている。

時刻制御とイベント制御

下図に、時刻制御(time driven)とイベント制御(event driven)の考え方の違いを比較して示している。

poisson-process-fig-time-and-event-driven

時刻制御については、観測時間を小さな時間間隔に区切って、区間ごとに到着確率に沿って到着の有無を決めながら、時刻を前に進めていく。

イベント制御の場合は、ポアソン過程で到着時間間隔が指数分布に従うことを利用して、指数乱数を発生させながら順次に到着時刻を算出していく。

関連リンク

 

逆関数による乱数の発生

/ tau / コメントする

問題

確率変数Xが確率分布F(X)に、確率変数Uが[0, 1)上の一様分布に従うとする。このときF^{-1} (U)は確率分布Fに従う。

下図にもあるように、確率分布関数が立っているところ、すなわち確率密度の高いところが高くなるような乱数が生成されることになるので、直感的にわかりやすい。

stat-inverse-function-probability-number

証明

Uが一様分布に従うことを以下のように表す。

(1)   \begin{equation*} P(U \le u) = u \quad (0 \le u < 1) \end{equation*}

確率分布関数F(X)は単調増加で、その逆関数も単調増加だから、

(2)   \begin{equation*} U \le u \Leftrightarrow F^{-1} (U) \le F^{-1} (u) \end{equation*}

これより、

(3)   \begin{equation*} P(U \le u) = P(F^{-1}(U) \le F^{-1}(u)) = u \end{equation*}

ここでF^{-1}(u) = xとおくと、u = F(x)だから、

(4)   \begin{equation*} P(F^{-1}(U) \le x) = F(x) \end{equation*}

すなわち確率変数F^{-1}が確率分布F(x)に従うことを意味している。

指数分布の例

指数関数の確率分布関数は以下の形をとる。

(5)   \begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}

これの逆関数系は以下のとおり。

(6)   \begin{equation*} F^{-1}(U) = - \frac{1}{\lambda} \ln( 1 - u) \end{equation*}

上式のuに一様乱数列を入れることで、計算結果は指数分布に従う乱数列として得られる。

統計分析言語Rで確認したところ、一様乱数からきれいな指数乱数が得られている。

stat-inverse-function-exponential-random-number

 

 

R – sapplyについて

/ tau / コメントする

ベクトル演算とsapplyの違い

ベクトルの各要素に関数を作用させたいとき、普通は次のようにする。

これを、sapplyを使って次のようにも書ける。

一見すると何ら違いはないように見えるが、次のような場合に違いが出てくる。

ベクトル演算の場合は、全ての要素に対して同じ演算結果が適用されるる。このためrunif(1)が1度だけ計算され、各要素にその結果が適用されるので、全要素が同じ値になる。

sapplyの場合は、各要素に対して毎回演算が行われる、このため各要素ごとにrunif(1)が計算されて適用されるので、各要素の値が異なる。

各要素に新規の計算結果を入れたいとき

各要素の初期値と無関係に要素に計算結果を適用したいと意図したとき、関数にダミー変数を書いておいて処理する。

例えば以下の例では、5つの要素に新たな乱数を発生させてセットしようとしている。

sapplyの場合は期待通りの結果。この場合は関数に引数が要求されるので、dummyという引数を与えている。

関数の引数にベクトルを入れると、その引数に対して1回だけ乱数を発生させるので、結果は1個の数値。

rep()関数の引数にf()を適用すると、1回だけ発生した乱数がすべての要素に適用されている。

複数の引数を持つ関数の場合

次の例は、各要素それぞれに0～2の範囲の乱数をセットしている。

sapplyに渡す関数が2つ以上の引数を持つときは、関数に続けて残りの引数を渡せばよい。