概要
Pythonのnumpyで統計量を扱う場合、分散・共分散で注意を要する点がある。Excelの関数でも同様だが、分散・共分散が標本値からそのまま計算した値か、不偏推定量として計算した値か、ということを意識する必要がある。
ここでは、ndarrayから律義に計算した値と、numpyの組み込み関数から計算した値を比較してみる。
標本数・総和・平均
標本として与えた配列の要素数、全要素の和、総和を要素数で除した値で、そのまま母集団の不偏推定量。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np x = np.array([1, 2, 3, 4, 5]) n = len(x) sum_x = x.sum() mean_x = sum_x / n print(n) print(sum_x) print(mean_x, x.mean()) # 5 # 15 # 3.0 3.0 |
分散・標準偏差の食い違い
var()、std()は標本の分散・標準偏差
分散・共分散については、提供されたメソッドvar()、std()は標本数で除した標本分散・共分散となる。
|
1 2 3 4 5 6 7 8 9 |
x = np.array([1, 2, 3, 4, 5]) n = len(x) var_x = np.sum((x - x.mean())**2) / n std_x = np.sqrt(var_x) print(var_x, x.var()) print(std_x, x.std()) # 2.0 2.0 # 1.4142135623730951 1.4142135623730951 |
不偏分散やその平方根を求める場合は、var()、std()の引数でddof=1とする。
cov()で与えられるのは不偏推定量
numpy.cov()で二つの一次元配列の分散・共分散行列を得ることができる。分散共分散行列は
![\begin{equation*} \left[ \begin{array}{ll} {\rm Var}(X) & {\rm Cov}(XY) \\ {\rm Cov}(XY) & {\rm Var}(Y) \end{array} \right] \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-fa27b6d6e33c071624930500984497df_l3.png "Rendered by QuickLaTeX.com")
で定義されるが、以下の計算結果の対角要素は、先の分散の計算結果(2.0)と異なっている。
|
1 2 3 4 5 6 |
x = np.array([1, 2, 3, 4, 5]) y = np.array([1, 2, 3, 4, 5]) print(np.cov(x, y)) # [[2.5 2.5] # [2.5 2.5]] |
これらの値は、分散を標本分散ではなく不偏推定量で計算しているためで、試しに先の計算を不偏分散で計算してみると結果は整合する。
ちなみに標本分散は偏差の二乗和を標本数nで割り、不偏分散はn-1で割る。
|
1 2 3 4 5 6 |
x = np.array([1, 2, 3, 4, 5]) n = len(x) var_x = np.sum((x - x.mean())**2) / (n - 1) print(var_x) # 2.5 |
共分散にも注意
上記では分散について確認したが、共分散についても注意が必要。
共分散は一般に以下で定義される。
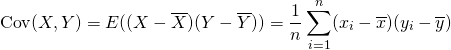
これに従って計算した結果。
|
1 2 3 4 5 6 7 |
x = np.array([1, 2, 3, 4, 5]) y = np.array([1, 2, 3, 4, 5]) n = len(x) cov_xy = np.sum((x - x.mean())*(y - y.mean())) / n print(cov_xy) # 2.0 |
この結果は、numpy.cov()で計算した非対角要素2.5と食い違う。
ここでn→n-1として計算しなおすと結果は2.5となり同じ値となる。
共分散用は、たとえば回帰分析の残差変動を計算するときに利用するが、その時には標本の共分散を使うので、注意が必要。
numpyで統計計算をする際、特に共分散については、律義に定義式から計算するのがよさそう。