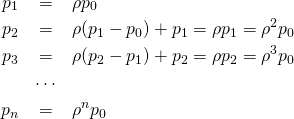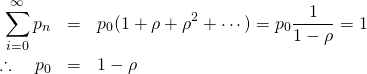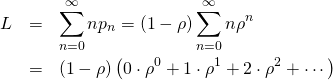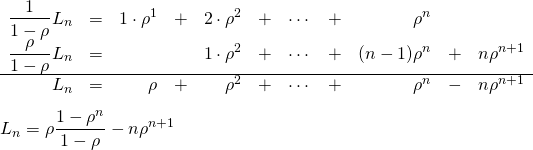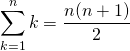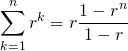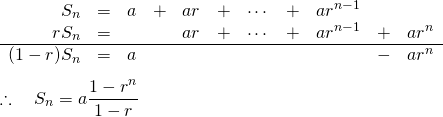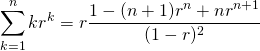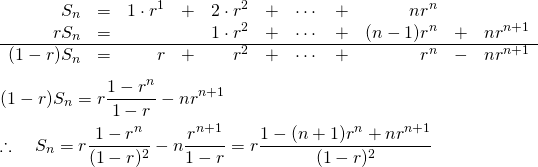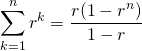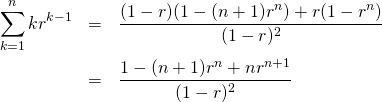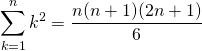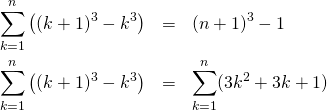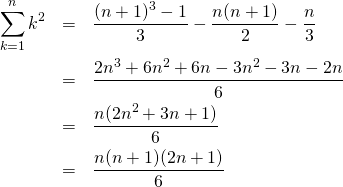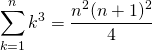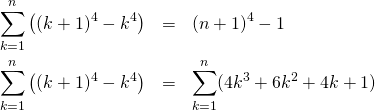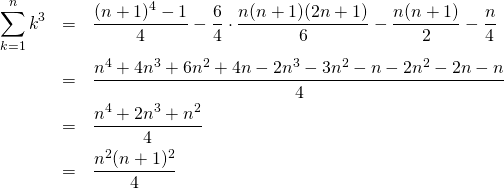R – 画面表示

2016-09-18 / tau / コメントする

オブジェクトの直接表示

オブジェクトを直接入力すると、その内容が表示される。

> c(1, 2, 3)
[1] 1 2 3
> x = 1:5
> x
[1] 1 2 3 4 5
> (y = seq(1, 5))
[1] 1 2 3 4 5

> c(1, 2, 3)

[1] 1 2 3

> x = 1:5

> x

[1] 1 2 3 4 5

> (y = seq(1, 5))

[1] 1 2 3 4 5

スクリプトファイルでも行頭にオブジェクトを書くと、その行の実行時点でオブジェクトの内容が表示される。

ただし条件判断やループの場合は、文でもブロックでも表示はされない。

例えば以下のスクリプトの場合、

1:5

for (i in 1:5) {
  1:i
}

for (i in 1:5) 1:i

1:5

for (i in 1:5) {

1:i

}

for (i in 1:5) 1:i

表示されるのは1行目だけ。

> 1:5print
[1] 1 2 3 4 5
> 
> for (i in 1:5) {
+   1:i
+ }
> 
> for (i in 1:5) 1:i

> 1:5print

[1] 1 2 3 4 5

> for (i in 1:5) {

+ 1:i

+ }

> for (i in 1:5) 1:i

print()～一般的な表示

オブジェクトの内容をそのまま表示する。

デフォルトでは文字列が””で囲われるが、quote=Fを指定すると””が表示されなくなる。

> x <- c("one", "two", "three")
> print(x)
[1] "one"   "two"   "three"
> x <- c("one", "two", "three")
> print(x)
[1] "one"   "two"   "three"
> print(x, quote=F)
[1] one   two   three

> x <- c("one", "two", "three")

> print(x)

[1] "one" "two" "three"

> x <- c("one", "two", "three")

> print(x)

[1] "one" "two" "three"

> print(x, quote=F)

[1] one two three

page()～別ウィンドウでの表示

page()関数ごとに別ウィンドウが立ち上がり、オブジェクトが表示される。大量のデータを表示するときに便利。

デフォルトではmethod="dput"が指定され、オブジェクトの定義表現が表示される。

オブジェクトの内容を表示するときは、明示的にmethod="print"を指定する。

x <- 1:100
page(x, method="dput")
page(x, method="print")

x <- 1:100

page(x, method="dput")

page(x, method="print")

1つ目のpage()関数で別ウィンドウが立ち上がり、以下のように表示される。

1:100

1:100

2つ目のpage()関数で2つ目の別ウィンドウが立ち上がり、以下のように表示される。

  [1]   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
 [19]  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36
 [37]  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53  54
 [55]  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72
 [73]  73  74  75  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90
 [91]  91  92  93  94  95  96  97  98  99 100

[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

[19] 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

[37] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54

[55] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72

[73] 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90

[91] 91 92 93 94 95 96 97 98 99 100

cat()～文字列の表示

cat()関数は、括弧内の文字列をそのまま出力する。

catは最後に改行をつけないので、改行させたい時は”\n”を付ける。

> cat("This is test for cat()\n")
This is test for cat()

1 2	> cat("This is test for cat()\n") This is test for cat()

str()～オブジェクト情報付き表示

要約されたオブジェクトの情報を付けて内容を表示する。

> str(seq(1, 5))
 int [1:5] 1 2 3 4 5
> str(c("one", "two", "three"))
 chr [1:3] "one" "two" "three"

> str(seq(1, 5))

int [1:5] 1 2 3 4 5

> str(c("one", "two", "three"))

chr [1:3] "one" "two" "three"

summary()～データの要約を表示する。

オブジェクトの内容に応じた要約情報を表示する。

summaryは特に統計データの要約に重要。たとえば▲データフレームの集計▲を参照。

> summary(seq(1, 5))
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
      1       2       3       3       4       5 
> summary(c("one", "two", "three"))
   Length     Class      Mode 
        3 character character

> summary(seq(1, 5))

Min. 1st Qu. Median Mean 3rd Qu. Max.

1 2 3 3 4 5

> summary(c("one", "two", "three"))

Length Class Mode

3 character character

待ち行列(M/M/1)の再現 – イベント制御

2016-09-18 / tau / コメントする

考え方

M/M1待ち行列のシミュレーションを、イベント制御(event driven)で行う。M/M/1待ち行列の解析的アプローチはこちら。言語はRを使う。なお時刻制御によるケースはこちら。

計算手順のブロックは次の3つ。

全てのトランザクションの到着時刻を指数分布に従って発生させる
時刻0から指数分布に従ってサービス時間を1つずつ発生させる
1. 待ち状態のトランザクションがあればすぐに次のサービスを開始
2. 待ち状態のトランザクションがなければ、次のトランザクション到着時にサービス開始
待ち行列長の推移を集計し、結果を表示する

定数定義

##########
# 定数設定
##########

# トランザクションの到着率とサービス率
lambda <- 1/10
mu <- 1/5

# 生成するトランザクションの数
# このうち真ん中のの1/3だけ最終的に使う
num.trs <- 3000

##########

# 定数設定

##########

# トランザクションの到着率とサービス率

lambda <- 1/10

mu <- 1/5

# 生成するトランザクションの数

# このうち真ん中のの1/3だけ最終的に使う

num.trs <- 3000

トランザクションの到着時刻の発生

到着時間間隔を乱数で発生させてトランザクションの到着時刻を発生させる。手順についてはイベント制御によるポアソン過程のシミュレーションを参照。

#################################
# 第1ステップ
# トランザクションの時系列データを生成
#################################

# trs:トランザクション
# svc:サービス
# arv:到着
# sta:開始
# end:終了
# wat:待ち時間
trs.arv <- numeric(num.trs)
trs.svc.sta <- numeric(num.trs)
trs.svc.end <- numeric(num.trs)
svc.sta <- c(0)
svc.end <- numeric(0)
trs.wat.svc.sta <- numeric(num.trs)
trs.wat.svc.end <- numeric(num.trs)

# 全てのトランザクションの到着時刻を指数分布の間隔で生成
exp.rand <- rexp(num.trs, rate=lambda)
for (i in 2:num.trs)
  trs.arv[i] <- trs.arv[i-1] + exp.rand[i-1]

#################################

# 第1ステップ

# トランザクションの時系列データを生成

#################################

# trs:トランザクション

# svc:サービス

# arv:到着

# sta:開始

# end:終了

# wat:待ち時間

trs.arv <- numeric(num.trs)

trs.svc.sta <- numeric(num.trs)

trs.svc.end <- numeric(num.trs)

svc.sta <- c(0)

svc.end <- numeric(0)

trs.wat.svc.sta <- numeric(num.trs)

trs.wat.svc.end <- numeric(num.trs)

# 全てのトランザクションの到着時刻を指数分布の間隔で生成

exp.rand <- rexp(num.trs, rate=lambda)

for (i in 2:num.trs)

trs.arv[i] <- trs.arv[i-1] + exp.rand[i-1]

サービス時間の計算

下図に考え方を示す。

queue-mm1-event-driven-fig1

時刻0でトランザクション1到着
時刻0でサービス1開始
指数乱数でサービス1の終了時刻を計算
終了時刻より前に次のトランザクション2が到着している
すぐにトランザクション2に対してサービス2を開始
サービス2の終了時刻を指数乱数で計算
終了時刻より前に次のトランザクション3が到着している
すぐにトランザクション3に対してサービス3を開始
サービス3の終了時刻を指数乱数で計算
次のトランザクション4の到着は終了時刻より後
トランザクション4の到着と同時にサービス4を開始する
サービス4の終了時刻を指数乱数で計算

#########################
# 第2ステップ
# サービスの開始・終了時刻の計算
#########################

# 時刻0でトランザクション到着、サービス開始
it <- 1
is <- 1

# 全てのトランザクションに対して実行
while (it <= num.trs) {
  # 現在のサービスの終了時刻を指数分布で計算し、トランザクションを1つ解放
  svc.end[is] <- svc.sta[is] + rexp(1, rate=mu)
  trs.svc.end[it] <- svc.end[is]
  trs.wat.svc.end[it] <- trs.svc.end[it] - trs.arv[it]
  # 最後の客なら計算だけして終わり
  if (it == num.trs) break

  # 次のサービス開始
  is <- is + 1
  it <- it + 1

  if (trs.arv[it] < svc.end[is - 1]) {
  # 待ち行列に客がいる場合、すぐに先頭の客のサービスを開始
    trs.svc.sta[it] <- svc.sta[is] <- svc.end[is - 1]
  } else {
  # 待ち行列に客がいない場合、最初に到着する客に対してサービスを開始
    trs.svc.sta[it] <- svc.sta[is] <- trs.arv[it]
  }
  trs.wat.svc.sta[it] <- trs.svc.sta[it] - trs.arv[it]
}

# トランザクションに関するデータの集計
trs.time.sequence <- data.frame(
  arrive = trs.arv,
  start = trs.svc.sta,
  end = trs.svc.end,
  trs.time = trs.wat.svc.end,
  queue.time = trs.wat.svc.sta
)

#########################

# 第2ステップ

# サービスの開始・終了時刻の計算

#########################

# 時刻0でトランザクション到着、サービス開始

it <- 1

is <- 1

# 全てのトランザクションに対して実行

while (it <= num.trs) {

# 現在のサービスの終了時刻を指数分布で計算し、トランザクションを1つ解放

svc.end[is] <- svc.sta[is] + rexp(1, rate=mu)

trs.svc.end[it] <- svc.end[is]

trs.wat.svc.end[it] <- trs.svc.end[it] - trs.arv[it]

# 最後の客なら計算だけして終わり

if (it == num.trs) break

# 次のサービス開始

is <- is + 1

it <- it + 1

if (trs.arv[it] < svc.end[is - 1]) {

# 待ち行列に客がいる場合、すぐに先頭の客のサービスを開始

trs.svc.sta[it] <- svc.sta[is] <- svc.end[is - 1]

} else {

# 待ち行列に客がいない場合、最初に到着する客に対してサービスを開始

trs.svc.sta[it] <- svc.sta[is] <- trs.arv[it]

}

trs.wat.svc.sta[it] <- trs.svc.sta[it] - trs.arv[it]

}

# トランザクションに関するデータの集計

trs.time.sequence <- data.frame(

arrive = trs.arv,

start = trs.svc.sta,

end = trs.svc.end,

trs.time = trs.wat.svc.end,

queue.time = trs.wat.svc.sta

)

待ち行列長の推移の集計

以下の手順によっている。

トランザクションの到着時とサービス終了時の時刻を取り出し、時刻と増減値をデータフレームにまとめる
時刻順にソート
待ち行列長の推移を計算する

ここで、トランザクション数と待ち行列長には、到着したトランザクション自身はカウントしていない(長さ0も考慮するため)。

####################################
# 第3ステップ
# 時系列データから待ち行列変化時系列を生成
####################################

# トランザクション数の増減が発生した時刻を記録するベクトル
evt.time <- c(trs.time.sequence$arrive, trs.time.sequence$end)
# システムのトランザクション数の増減を記録するベクトル
# arriveで+1、endで-1
trs.change <-c(rep(+1, num.trs), rep(-1, num.trs))
# サービス中のトランザクションを除いた待ち行列長を記録するベクトル
queue <- rep(0, num.trs*2)

# トランザクション数と待ち行列をデータフレーム化
system.trs <- data.frame(
  time = evt.time,
  change = trs.change,
  transactions = rep(0, 2*num.trs))
system.trs <- system.trs[order(system.trs$time),]
rownames(system.trs) <- 1:nrow(system.trs)

# 時刻0での待ち行列から、その後の待ち行列長を計算
# 注意点：トランザクション数や待ち行列長に自分自身は数えない
system.trs$transactions[1] <- 0
queue[1] <- 0
for (i in 2:nrow(system.trs)) {
  n <- system.trs$transactions[i] <-
    system.trs$transactions[i-1] + system.trs$change[i]
  if (n <= 1) queue[i] <- 0 else queue[i] <- n - 1
}
system.trs <- cbind(system.trs, queue)

# トランザクション到着時のトランザクション数と待ち行列長を抜き出し
# 総括データフレームに集約
temp.frame <- system.trs[system.trs$change==1,]
trs.time.sequence <- cbind(trs.time.sequence, transactions=temp.frame$transactions)
trs.time.sequence <- cbind(trs.time.sequence, queue=temp.frame$queue)

####################################

# 第3ステップ

# 時系列データから待ち行列変化時系列を生成

####################################

# トランザクション数の増減が発生した時刻を記録するベクトル

evt.time <- c(trs.time.sequence$arrive, trs.time.sequence$end)

# システムのトランザクション数の増減を記録するベクトル

# arriveで+1、endで-1

trs.change <-c(rep(+1, num.trs), rep(-1, num.trs))

# サービス中のトランザクションを除いた待ち行列長を記録するベクトル

queue <- rep(0, num.trs*2)

# トランザクション数と待ち行列をデータフレーム化

system.trs <- data.frame(

time = evt.time,

change = trs.change,

transactions = rep(0, 2*num.trs))

system.trs <- system.trs[order(system.trs$time),]

rownames(system.trs) <- 1:nrow(system.trs)

# 時刻0での待ち行列から、その後の待ち行列長を計算

# 注意点：トランザクション数や待ち行列長に自分自身は数えない

system.trs$transactions[1] <- 0

queue[1] <- 0

for (i in 2:nrow(system.trs)) {

n <- system.trs$transactions[i] <-

system.trs$transactions[i-1] + system.trs$change[i]

if (n <= 1) queue[i] <- 0 else queue[i] <- n - 1

}

system.trs <- cbind(system.trs, queue)

# トランザクション到着時のトランザクション数と待ち行列長を抜き出し

# 総括データフレームに集約

temp.frame <- system.trs[system.trs$change==1,]

trs.time.sequence <- cbind(trs.time.sequence, transactions=temp.frame$transactions)

trs.time.sequence <- cbind(trs.time.sequence, queue=temp.frame$queue)

計算結果の表示

待ち行列時系列データの真ん中1/3を取り出し、トランザクション到着時のトランザクション数、待ち行列長を集計している。比較のため、それらの理論値も計算・表示している。

##############
# 計算結果の表示
##############

# 前後1/3を切り落とし
n <- nrow(trs.time.sequence)
calc.frame <- trs.time.sequence[(n/3):(n*2/3),]

# 到着率とサービス率から稼働率の理論値を計算
(rho <- lambda / mu)
# システム内の平均トランザクション数の理論値
(L <- rho / (1 - rho))
# 平均待ち行列長の理論値
(Lq <- rho^2 / (1 - rho))
# 平均トランザクションタイム
L / lambda
# 平均待ち時間
Lq / lambda

# トランザクション数、待ち行列長、総所要時間、待ち時間の平均値を表示
page(c(
mean(calc.frame$transactions),
mean(calc.frame$queue),
mean(calc.frame$trs.time),
mean(calc.frame$queue.time)
))

##############

# 計算結果の表示

##############

# 前後1/3を切り落とし

n <- nrow(trs.time.sequence)

calc.frame <- trs.time.sequence[(n/3):(n*2/3),]

# 到着率とサービス率から稼働率の理論値を計算

(rho <- lambda / mu)

# システム内の平均トランザクション数の理論値

(L <- rho / (1 - rho))

# 平均待ち行列長の理論値

(Lq <- rho^2 / (1 - rho))

# 平均トランザクションタイム

L / lambda

# 平均待ち時間

Lq / lambda

# トランザクション数、待ち行列長、総所要時間、待ち時間の平均値を表示

page(c(

mean(calc.frame$transactions),

mean(calc.frame$queue),

mean(calc.frame$trs.time),

mean(calc.frame$queue.time)

))

計算結果

1000個のデータからトランザクション数、待ち行列長を10回計算させ、それらについて割り戻したλの逆数、各データの平均と標準偏差を計算した。

ρ = 0.5のケース

λ = 1/10、μ = 1/5、ρ = 0.5のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 1、L_q = 0.5で、これらに対する待ち時間はT = 10、T_w = 5。

トランザクション数に関する計算結果は、かなり理論値と整合している。

	L	T	1/λ
1	0.977022977	9.767519297	9.997225783
2	1.181818182	12.00225815	10.1557569
3	1.236763237	11.35299611	9.17960348
4	0.87012987	9.097838003	10.45572427
5	0.943056943	9.652253196	10.23506933
6	1.132867133	11.09199315	9.791080377
7	0.958041958	9.28812046	9.694899459
8	1.347652348	12.61173676	9.358301328
9	1.058941059	10.13796162	9.573678846
10	0.867132867	9.19585645	10.60489897
AVG	1.057342657	10.41985332	9.854755454
STD	0.162710928	1.258385656	0.467315969

待ち行列についても、整合性は良い。

	L_q	T_q	1/λ
1	0.460539461	4.687171936	10.17756856
2	0.632367632	6.669065267	10.54618378
3	0.686313686	6.311337813	9.195995853
4	0.391608392	4.163816097	10.63260182
5	0.471528472	4.72111758	10.01237012
6	0.634365634	6.030695282	9.506655083
7	0.465534466	4.447464396	9.553458927
8	0.785214785	7.437052562	9.471360832
9	0.564435564	5.262195935	9.322934744
10	0.367632368	4.099711426	11.1516607
AVG	0.545954046	5.382962829	9.859736125
STD	0.136420649	1.159489377	0.655334793

ρ = 0.9のケース

λ = 1/10、μ = 1/9、ρ = 0.9のケース。平均トランザクション数と平均待ち行列長の理論値は、L = 9、L_q = 8.1で、これらに対する待ち時間はT = 90、T_w = 81。

トランザクション数に関する計算結果は、理論値よりも大きく出ている。

	L	T	1/λ
1	10.11288711	100.5733569	9.945068678
2	12.03096903	120.0280761	9.97659256
3	15.71128871	162.6168804	10.35032093
4	10.998002	110.2958229	10.02871457
5	18.26373626	178.496846	9.773293013
6	7.716283716	77.4353613	10.03531806
7	6.178821179	62.23838321	10.07285717
8	9.491508492	95.64553268	10.07695803
9	6.951048951	70.34023525	10.11936986
10	6.073926074	63.43794238	10.44430597
AVG	10.35284715	104.1108437	10.05625237
STD	4.076793696	40.26529308	0.192915047

待ち行列長についても傾向は同じ。

	L_q	T_q	1/λ
1	9.204795205	91.66512812	9.95841038
2	11.13286713	110.9692603	9.967716221
3	14.76723277	152.9773707	10.35924422
4	10.07392607	101.1184062	10.03763631
5	17.28271728	169.1669214	9.7882132
6	6.789210789	68.44424425	10.08132556
7	5.254745255	53.24239678	10.13225079
8	8.545454545	86.43775829	10.11505682
9	6.06993007	61.37562417	10.11142195
10	5.220779221	54.59901247	10.4580198
AVG	9.434165834	94.99961227	10.06974161
STD	4.051237304	40.07040651	0.193152208

稼働率をρが1に近づくと、計算結果に乖離がみられる。たとえばN = 10000個のデータについて計算してみても、傾向は変わらない。

待ち行列(M/M/1)

2016-09-17 / tau / コメントする

前提

時刻t～t + Δtの間に以下のいずれかの状態遷移が発生するとする。希少性の仮定から、2つ以上の事象が同時に起こることはなく、いずれか1つが発生するとする。

確率λΔtで1つのトランザクションが到着する
確率μΔtで1つのサービスが完了する
確率(1 – λΔt – μΔt)でトランザクションの到着もなくサービスも完了しない
- 本来は(1 – λΔt)(1 – μΔt)で表されるところ、これを展開してΔt²の項を無視してこの形になる
- あるいは指数分布の密度関数をMaclaurin展開して2時以上の項をo(Δt²)として消していってもよい

なお、M/M/1待ち行列のイベント制御による再現をR言語で試している。

状態方程式

システムの状態を、システム内のトランザクション数nで表す。nには、サービスを受けているトランザクションとサービスを待機しているトランザクションの数の和。

時刻tにおいてトランザクション数がnである状態確率をp_n(t)とすると、状態方程式は以下のようになる。

(1) $\begin{eqnarray*} p_n (t + \Delta t) &=& p_{n-1} \lambda \Delta t + p_n (t) (1 - \lambda \Delta t - \mu \Delta t) + p_{n+1} \mu \Delta t \\ p_{0}(t + \Delta t) &=& p_{0}(1 - \lambda \Delta t) + p_{1} \mu \Delta t \end{eqnarray*}$

まず式(1)の第1式について、

(2) $\begin{eqnarray*} \frac{dp_n (t)}{dt} &=& \lim_{\Delta t \rightarrow 0} \frac{p_n(t + \Delta t) - p_n (t)}{\Delta t} \\ &=& p_{n-1} \lambda - p_n (\lambda + \mu) + p_{n+1} \mu \end{eqnarray*}$

また第2式については、

(3) $\begin{eqnarray*} \frac{dp_0 (t)}{dt} &=& \lim_{\Delta t \rightarrow 0} \frac{p_0(t + \Delta t) - p_0 (t)}{\Delta t} \\ &=& - p_0 \lambda + p_1 \mu \end{eqnarray*}$

式(2)と式(3)を改めてまとめて書くと、

(4) $\begin{eqnarray*} \frac{dp_n (t)}{dt} &=& \lambda p_{n-1} - (\lambda + \mu) p_n + \mu p_{n+1} \\ \frac{dp_0 (t)}{dt} &=& - \lambda p_0 + \mu p_1 \end{eqnarray*}$

定常問題化と状態方程式の解

状態方程式においてt → ∞でトランザクション数の変化がなく一定値に収束するとして、次式を得る。

(5) $\begin{eqnarray*} \lambda p_{n-1} - (\lambda + \mu) p_n + \mu p_{n+1} &=& 0 \quad (n > 0) \\ - \lambda p_0 + \mu p_1 &=& 0 \end{eqnarray*}$

ここでρ = λ/μ < 0とおいて、

(6) $\begin{eqnarray*} \rho p_{n-1} - (1 + \rho) p_n + p_{n+1} &=& 0 \quad (n > 0) \\ - \rho p_0 + p_1 &=& 0 \end{eqnarray*}$

これは階差数列の式に変形できて、

(7) $\begin{eqnarray*} p_n - p_{n-1} &=& \rho (p_n - p_{n-1}) \\ p_1 &=& \rho p_0 \end{eqnarray*}$

上式から順次各項を求めると、

(8) $\begin{eqnarray*} p_1 &=& \rho p_0 \\ p_2 &=& \rho (p_1 - p_0) + p_1 = \rho p_1 = \rho ^2 p_0 \\ p_3 &=& \rho(p_2 - p_1) + p_2 = \rho p_2 = \rho ^3 p_0 \\ &\cdots& \\ p_n &=& \rho ^n p_0 \end{eqnarray*}$

全事象の和が1という条件から、以下の結果を得る。

(9) $\begin{eqnarray*} \sum_{i=0}^\infty p_n &=& p_0 (1 + \rho + \rho ^2 + \cdots ) = p_0 \frac{1}{1 - \rho} = 1 \\ \therefore \quad p_0 &=& 1 - \rho \end{eqnarray*}$

これより、システムの状態がnである確率は以下で表せる。

(10) $\begin{equation*} p _n &=& (1 - \rho) \rho ^n \end{equation*}$

ρの意味

ρ = λ / μは、単位時間当たりのサービス提供数に対する単位時間当たりのトラフィック到達数で、サービスの混み具合を表している。また、どの程度サービスが稼働しているか／利用されているか、とも言えるので、混雑度、平均稼働率／利用率、平均到達率、平均トラフィック密度などと呼ばれている。

平均トランザクション数と平均待ち行列長

システム内の平均トランザクション数Lは、

(11) $\begin{eqnarray*} L &=& \sum_{n=0}^\infty n p_n = (1 - \rho) \sum_{n=0}^\infty n \rho ^n \\ &=& (1 - \rho) \left(0 \cdot \rho^0 + 1 \cdot \rho^1 + 2 \cdot \rho^2 + \cdots \right) \end{eqnarray*}$

これを以下のように解く。

(12) $\begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} \displaystyle \frac{1}{1 - \rho} L_n &= &1 \cdot \rho ^1 &+ &2 \cdot \rho ^2 &+ &\cdots &+ &\n \rho^n \\ \displaystyle \frac{\rho}{1 - \rho} L_n &= & & &1 \cdot \rho^2 &+ &\cdots &+ &(n - 1) \rho^n &+ &n \rho^{n + 1} \\ \hline L_n &= &\rho &+ &\rho^2 &+ &\cdots &+ &\rho^n &- &n \rho^{n+1} \end{array} \\ \\ & &L_n = \rho \frac{1 - \rho^n}{1 - \rho} - n \rho^{n+1} \end{eqnarray*}$

よって、

(13) $\begin{equation*} L = \lim_{n \rightarrow \infty} L_n = \frac{\rho}{1 - \rho} \end{equation*}$

また平均待ち行列長については、サービス中のトランザクションを除いて考えて、

(14) $\begin{eqnarray*} L_q &=& 0 \cdot p_0 + 0 \cdot p_1 + 1 \cdot p_2 + 2 \cdot p_3 + \cdots\\ &=& (1 - \rho) \left( 1 \cdot \rho^2 + 2 \cdot \rho^3 + \cdots \right) \end{eqnarray*}$

これも以下のように解く。

(15) $\begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} \displaystyle \frac{1}{1 - \rho} L_qn &= &1 \cdot \rho ^2 &+ &2 \cdot \rho ^3 &+ &\cdots &+ &\n \rho^{n+1} \\ \displaystyle \frac{\rho}{1 - \rho} L_qn &= & & &1 \cdot \rho^3 &+ &\cdots &+ &(n - 1) \rho^{n + 1} &+ &n \rho^{n + 2} \\ \hline L_n &= &\rho^2 &+ &\rho^3 &+ &\cdots &+ &\rho^{n+1} &- &n \rho^{n+2} \end{array} \\ \\ & &L_n = \rho^2 \frac{1 - \rho^n}{1 - \rho} - n \rho^{n+2} \end{eqnarray*}$

よって、

(16) $\begin{equation*} L_q = \lim_{n \rightarrow \infty} L_qn = \frac{\rho^2}{1 - \rho} \end{equation*}$

リトルの法則(Litter’s law)

定常状態にある待ち行列において、トランザクションがシステムに到着してからサービスを終えるまでの時間の平均(平均応答時間)をTとすると、その間に平均してλTのトランザクションが到着することから、次式が成り立つ。

(17) $\begin{equation*} L = \lambda T \end{equation*}$

また、同じことが待ち行列長L_qと平均待ち時間T_qにも言えるので、

(18) $\begin{equation*} L_q = \lambda T_q \end{equation*}$

リトルの公式を使うと、待ち行列の長さと到着率から、平均待ち時間が計算できる。

(19) $\begin{eqnarray*} T &=& \frac{L}{\lambda} \\ T_q &=& \frac{L_q}{\lambda} \end{eqnarray*}$

たとえば客の列に到着したときの行列の人数を数え、その後到着する客の数や出ていく客の数から到着率を推定することで、待ち時間を推定できる。

R – データフレームの参照・変更

2016-09-15 / tau / コメントする

データフレーム全体の参照

データフレームの名前そのもので、データフレームの内容を参照できる。列名(name, age)や項目名(“1″～”3”)も含めて参照される。

> name.data <- c("John", "Alice", "Dick")
> age.data <- c(35, 28, 42)
> data <- data.frame(name=name.data, age=age.data)
> data$name <- as.character(data$name)
> 
> data
   name age
1  John  35
2 Alice  28
3  Dick  42

> name.data <- c("John", "Alice", "Dick")

> age.data <- c(35, 28, 42)

> data <- data.frame(name=name.data, age=age.data)

> data$name <- as.character(data$name)

> data

name age

1 John 35

2 Alice 28

3 Dick 42

データフレームの行数・列数の参照

nrow()関数、ncol()関数でデータフレームの行数、列数を参照できる。dim()関数は(行数, 列数)のベクトルを返す。

> nrow(data)
[1] 3
> ncol(data)
[1] 2
> dim(data)
[1] 3 2

> nrow(data)

[1] 3

> ncol(data)

[1] 2

> dim(data)

[1] 3 2

データフレームの内容の参照・変更

列名・項目名の参照・変更

列名はnames()関数かcolnames()関数で、項目名はrownames()関数で取得できる。

> name.data <- c("John", "Alice", "Dick")
> age.data <- c(35, 28, 42)
> data <- data.frame(name=name.data, age=age.data)
> data$name <- as.character(data$name)
> 
> data
   name age
1  John  35
2 Alice  28
3  Dick  42
> 
> names(data)
[1] "name" "age" 
> 
> colnames(data)
[1] "name" "age" 
> 
> rownames(data)
[1] "1" "2" "3"

> name.data <- c("John", "Alice", "Dick")

> age.data <- c(35, 28, 42)

> data <- data.frame(name=name.data, age=age.data)

> data$name <- as.character(data$name)

> data

name age

1 John 35

2 Alice 28

3 Dick 42

> names(data)

[1] "name" "age"

> colnames(data)

[1] "name" "age"

> rownames(data)

[1] "1" "2" "3"

列名や項目名は、それぞれの参照関数にベクトルを代入することで変更できる。

> names(data) <- c("NAME", "AGE")
> rownames(data) <- c("a", "b", "c")
> data
   NAME AGE
a  John  35
b Alice  28
c  Dick  42

> names(data) <- c("NAME", "AGE")

> rownames(data) <- c("a", "b", "c")

> data

NAME AGE

a John 35

b Alice 28

c Dick 42

データフレームの要素の参照・変更

行・列を直接指定して参照する場合、列の場合は列名を指定するか列番号で、行の場合は行番号を指定して参照する。行・列の番号を指定して1つのデータを取得することもできる。

行番号を指定する場合は後ろに、列番号を指定する場合は前に”,”をつける必要があり、これは後述の行の抽出の場合に重要になる。

なお、参照した要素の右に代入文を書くことで、その要素や業・列の内容を変更できる。

> name.data <- c("John", "Alice", "Dick")
> age.data <- c(35, 28, 42)
> data <- data.frame(name=name.data, age=age.data)
> data$name <- as.character(data$name)
> 
> data
   name age
1  John  35
2 Alice  28
3  Dick  42
> 
> data$age
[1] 35 28 42
> 
> data[,2]
[1] 35 28 42
> 
> data[1,]
  name age
1 John  35
> 
> data[3,2]
[1] 42

> name.data <- c("John", "Alice", "Dick")

> age.data <- c(35, 28, 42)

> data <- data.frame(name=name.data, age=age.data)

> data$name <- as.character(data$name)

> data

name age

1 John 35

2 Alice 28

3 Dick 42

> data$age

[1] 35 28 42

> data[,2]

[1] 35 28 42

> data[1,]

name age

1 John 35

> data[3,2]

[1] 42

行・列の追加と削除

行・列の追加

行の追加はrbind()関数で、列の追加はcbind()関数で行う。

これらの関数は元のデータフレームを変更せず、新たなデータフレームを結果として返す。

rbindの注意点として、文字型を意図した項目はあらかじめFactor型から文字型に変更しておかないと、文字列を含んだデータを結合しようとするとエラーになる。

cbindの注意点としては、デフォルトでは引数の変数名が項目名にあてられる。直接c(…)と書いたりすると、それがそのまま項目名になってしまう。

【追記】　以下の例ではrbindの引数にベクトルを渡しているが、文字列と数値が混在している下記のような例では、これは危ない→rbindについてを参照

> name.data <- c("John", "Alice", "Dick")
> age.data <- c(35, 28, 42)
> data <- data.frame(name=name.data, age=age.data)
> data$name <- as.character(data$name)
> 
> data
   name age
1  John  35
2 Alice  28
3  Dick  42
> 
> rbind(data, c("Elen", 32))
   name age
1  John  35
2 Alice  28
3  Dick  42
4  Elen  32
> 
> height <- c(180, 162, 172)
> cbind(data, height)
   name age height
1  John  35    180
2 Alice  28    162
3  Dick  42    172

> name.data <- c("John", "Alice", "Dick")

> age.data <- c(35, 28, 42)

> data <- data.frame(name=name.data, age=age.data)

> data$name <- as.character(data$name)

> data

name age

1 John 35

2 Alice 28

3 Dick 42

> rbind(data, c("Elen", 32))

name age

1 John 35

2 Alice 28

3 Dick 42

4 Elen 32

> height <- c(180, 162, 172)

> cbind(data, height)

name age height

1 John 35 180

2 Alice 28 162

3 Dick 42 172

行・列の削除

行や列の番号を指定して削除する場合は、番号にマイナスをつける。範囲指定も可能。

行・列の追加と同じく、これらの操作も元のデータフレームを変更せず、新たなデータフレームを結果として返す。

> name.data <- c("John", "Alice", "Dick")
> age.data <- c(35, 28, 42)
> height.data <- c(180, 162, 172)
> data <- data.frame(name=name.data, age=age.data, height=height.data)
> 
> data
   name age height
1  John  35    180
2 Alice  28    162
3  Dick  42    172
> 
> data[-2,]
  name age height
1 John  35    180
3 Dick  42    172
> 
> data[,-2]
   name height
1  John    180
2 Alice    162
3  Dick    172
> 
> data[-1:-2,]
  name age height
3 Dick  42    172

> name.data <- c("John", "Alice", "Dick")

> age.data <- c(35, 28, 42)

> height.data <- c(180, 162, 172)

> data <- data.frame(name=name.data, age=age.data, height=height.data)

> data

name age height

1 John 35 180

2 Alice 28 162

3 Dick 42 172

> data[-2,]

name age height

1 John 35 180

3 Dick 42 172

> data[,-2]

name height

1 John 180

2 Alice 162

3 Dick 172

> data[-1:-2,]

name age height

3 Dick 42 172

データの抽出

列項目の条件を指定して、要素を抽出することができる。

指定の条件の後に”,”をつけるのを忘れないこと。これは行要素に対して条件指定していることを表している。

> name.data <- c("John", "Gene", "Jack", "Luice", "Elen")
> gender.data <- c("M", "F", "M", "M", "F")
> height.data <- c(165, 160, 170, 178, 157)
> weight.data <- c(62, 56, 75, 82, 58)
> qualified.data <- c(T, F, T, F, T)
> 
> data <- data.frame(
+   name=name.data,
+   gender=gender.data,
+   height=height.data,
+   weight=weight.data,
+   qualified=qualified.data
+ )
> data$name <- as.character(data$name)
> 
> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE
> 
> data[data$name=="Luice",]
   name gender height weight qualified
4 Luice      M    178     82     FALSE
> 
> data[data$gender=="F",]
  name gender height weight qualified
2 Gene      F    160     56     FALSE
5 Elen      F    157     58      TRUE
> 
> data[data$height>160,]
   name gender height weight qualified
1  John      M    165     62      TRUE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
> 
> data[weight>=60 & qualified==T,]
  name gender height weight qualified
1 John      M    165     62      TRUE
3 Jack      M    170     75      TRUE

> name.data <- c("John", "Gene", "Jack", "Luice", "Elen")

> gender.data <- c("M", "F", "M", "M", "F")

> height.data <- c(165, 160, 170, 178, 157)

> weight.data <- c(62, 56, 75, 82, 58)

> qualified.data <- c(T, F, T, F, T)

> data <- data.frame(

+ name=name.data,

+ gender=gender.data,

+ height=height.data,

+ weight=weight.data,

+ qualified=qualified.data

+ )

> data$name <- as.character(data$name)

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

> data[data$name=="Luice",]

name gender height weight qualified

4 Luice M 178 82 FALSE

> data[data$gender=="F",]

name gender height weight qualified

2 Gene F 160 56 FALSE

5 Elen F 157 58 TRUE

> data[data$height>160,]

name gender height weight qualified

1 John M 165 62 TRUE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

> data[weight>=60 & qualified==T,]

name gender height weight qualified

1 John M 165 62 TRUE

3 Jack M 170 75 TRUE

抽出操作はもとのデータフレームに影響を与えず、結果は新たなデータフレームとして返される。

> subdata <- data[data$gender=="F",]
> 
> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE
> 
> subdata
  name gender height weight qualified
2 Gene      F    160     56     FALSE
5 Elen      F    157     58      TRUE

> subdata <- data[data$gender=="F",]

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

> subdata

name gender height weight qualified

2 Gene F 160 56 FALSE

5 Elen F 157 58 TRUE

R – データフレームのソート

2016-09-15 / tau / 2件のコメント

order()関数

以下のデータを準備する。

name.data <- c("John", "Gene", "Jack", "Luice", "Elen")
gender.data <- c("M", "F", "M", "M", "F")
height.data <- c(165, 160, 170, 178, 157)
weight.data <- c(62, 56, 75, 82, 58)
qualified.data <- c(T, F, T, F, T)

data <- data.frame(
  name=name.data,
  gender=gender.data,
  height=height.data,
  weight=weight.data,
  qualified=qualified.data
)

name.data <- c("John", "Gene", "Jack", "Luice", "Elen")

gender.data <- c("M", "F", "M", "M", "F")

height.data <- c(165, 160, 170, 178, 157)

weight.data <- c(62, 56, 75, 82, 58)

qualified.data <- c(T, F, T, F, T)

data <- data.frame(

name=name.data,

gender=gender.data,

height=height.data,

weight=weight.data,

qualified=qualified.data

)

このデータフレームをheightの項目の昇順のオーダーでソートしたいとする。

order()関数というのがあって、引数の項目でソートしたときに元データの項目番号がどういう順番で並ぶかを返してくれる。

> data$height
[1] 165 160 170 178 157
> order(data$height)
[1] 5 2 1 3 4

> data$height

[1] 165 160 170 178 157

> order(data$height)

[1] 5 2 1 3 4

たとえば1番目のデータは1番小さい157で、これは5番目のデータ。2番目のデータは2番目に小さい160で2番目のデータ・・・という風に、heightデータを昇順に並べた時の元データの項目番号の並びを教えてくれる。

rank()関数がデータを昇順に並べた時の、そのデータのソート後の順番を返すのとは違う点に注意。

この結果を元のデータフレームの行部分に使うと、その順番で並べ替えられたデータを返してくれる。

> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE
> 
> data[order(data$height),]
   name gender height weight qualified
5  Elen      F    157     58      TRUE
2  Gene      F    160     56     FALSE
1  John      M    165     62      TRUE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

> data[order(data$height),]

name gender height weight qualified

5 Elen F 157 58 TRUE

2 Gene F 160 56 FALSE

1 John M 165 62 TRUE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

降順ソート

データを降順にソートしたい時は、decreasing=Tで指示する。

> data[order(data$height, decreasing=T),]
   name gender height weight qualified
4 Luice      M    178     82     FALSE
3  Jack      M    170     75      TRUE
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
5  Elen      F    157     58      TRUE

> data[order(data$height, decreasing=T),]

name gender height weight qualified

4 Luice M 178 82 FALSE

3 Jack M 170 75 TRUE

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

5 Elen F 157 58 TRUE

複数列のソートなど

以下の例は、数値以外でもソートできることと、複数のオーダーを組み合わせたソートの例を示している。

> data[order(data$qualified, data$weight),]
   name gender height weight qualified
2  Gene      F    160     56     FALSE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE
1  John      M    165     62      TRUE
3  Jack      M    170     75      TRUE

> data[order(data$qualified, data$weight),]

name gender height weight qualified

2 Gene F 160 56 FALSE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

1 John M 165 62 TRUE

3 Jack M 170 75 TRUE

行番号の変更

ソート後に行ラベルを振り直したい場合は、rownames()の内容を変更する。

> data <- data[order(data$height),]
> data
   name gender height weight qualified
5  Elen      F    157     58      TRUE
2  Gene      F    160     56     FALSE
1  John      M    165     62      TRUE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
> rownames(data) <- 1:nrow(data)
> data
   name gender height weight qualified
1  Elen      F    157     58      TRUE
2  Gene      F    160     56     FALSE
3  John      M    165     62      TRUE
4  Jack      M    170     75      TRUE
5 Luice      M    178     82     FALSE

> data <- data[order(data$height),]

> data

name gender height weight qualified

5 Elen F 157 58 TRUE

2 Gene F 160 56 FALSE

1 John M 165 62 TRUE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

> rownames(data) <- 1:nrow(data)

> data

name gender height weight qualified

1 Elen F 157 58 TRUE

2 Gene F 160 56 FALSE

3 John M 165 62 TRUE

4 Jack M 170 75 TRUE

5 Luice M 178 82 FALSE

R – データフレームの集計

2016-09-15 / tau / コメントする

summary()関数で、データ全体の集計が行える。

> name.data <- c("John", "Gene", "Jack", "Luice", "Elen")
> gender.data <- c("M", "F", "M", "M", "F")
> height.data <- c(165, 160, 170, 178, 157)
> weight.data <- c(62, 56, 75, 82, 58)
> qualified.data <- c(T, F, T, F, T)
> 
> data <- data.frame(
+   name=name.data,
+   gender=gender.data,
+   height=height.data,
+   weight=weight.data,
+   qualified=qualified.data
+ )
> data$name <- as.character(data$name)
> 
> summary(data)
     name           gender     height        weight     qualified      
 Length:5           F:2    Min.   :157   Min.   :56.0   Mode :logical  
 Class :character   M:3    1st Qu.:160   1st Qu.:58.0   FALSE:2        
 Mode  :character          Median :165   Median :62.0   TRUE :3        
                           Mean   :166   Mean   :66.6   NA's :0        
                           3rd Qu.:170   3rd Qu.:75.0                  
                           Max.   :178   Max.   :82.0

> name.data <- c("John", "Gene", "Jack", "Luice", "Elen")

> gender.data <- c("M", "F", "M", "M", "F")

> height.data <- c(165, 160, 170, 178, 157)

> weight.data <- c(62, 56, 75, 82, 58)

> qualified.data <- c(T, F, T, F, T)

> data <- data.frame(

+ name=name.data,

+ gender=gender.data,

+ height=height.data,

+ weight=weight.data,

+ qualified=qualified.data

+ )

> data$name <- as.character(data$name)

> summary(data)

name gender height weight qualified

Length:5 F:2 Min. :157 Min. :56.0 Mode :logical

Class :character M:3 1st Qu.:160 1st Qu.:58.0 FALSE:2

Mode :character Median :165 Median :62.0 TRUE :3

Mean :166 Mean :66.6 NA's :0

3rd Qu.:170 3rd Qu.:75.0

Max. :178 Max. :82.0

by()関数によって、特定のデータの層別に集計することができる。

> by(data, data$gender, summary)
data$gender: F
     name           gender     height          weight     qualified      
 Length:2           F:2    Min.   :157.0   Min.   :56.0   Mode :logical  
 Class :character   M:0    1st Qu.:157.8   1st Qu.:56.5   FALSE:1        
 Mode  :character          Median :158.5   Median :57.0   TRUE :1        
                           Mean   :158.5   Mean   :57.0   NA's :0        
                           3rd Qu.:159.2   3rd Qu.:57.5                  
                           Max.   :160.0   Max.   :58.0                  
--------------------------------------------------------- 
data$gender: M
     name           gender     height          weight     qualified      
 Length:3           F:0    Min.   :165.0   Min.   :62.0   Mode :logical  
 Class :character   M:3    1st Qu.:167.5   1st Qu.:68.5   FALSE:1        
 Mode  :character          Median :170.0   Median :75.0   TRUE :2        
                           Mean   :171.0   Mean   :73.0   NA's :0        
                           3rd Qu.:174.0   3rd Qu.:78.5                  
                           Max.   :178.0   Max.   :82.0

> by(data, data$gender, summary)

data$gender: F

name gender height weight qualified

Length:2 F:2 Min. :157.0 Min. :56.0 Mode :logical

Class :character M:0 1st Qu.:157.8 1st Qu.:56.5 FALSE:1

Mode :character Median :158.5 Median :57.0 TRUE :1

Mean :158.5 Mean :57.0 NA's :0

3rd Qu.:159.2 3rd Qu.:57.5

Max. :160.0 Max. :58.0

---------------------------------------------------------

data$gender: M

name gender height weight qualified

Length:3 F:0 Min. :165.0 Min. :62.0 Mode :logical

Class :character M:3 1st Qu.:167.5 1st Qu.:68.5 FALSE:1

Mode :character Median :170.0 Median :75.0 TRUE :2

Mean :171.0 Mean :73.0 NA's :0

3rd Qu.:174.0 3rd Qu.:78.5

Max. :178.0 Max. :82.0

もちろん、個別の数値データについて各種代表値を計算することもできる。

> max(data$height)
[1] 178
> min(data$height)
[1] 157
> range(data$height)
[1] 157 178
> sum(data$height)
[1] 830
> mean(data$height)
[1] 166
> var(data$height)
[1] 69.5
> sd(data$height)
[1] 8.336666

> max(data$height)

[1] 178

> min(data$height)

[1] 157

> range(data$height)

[1] 157 178

> sum(data$height)

[1] 830

> mean(data$height)

[1] 166

> var(data$height)

[1] 69.5

> sd(data$height)

[1] 8.336666

R – データフレームの列の非因子化

2016-09-15 / tau / コメントする

ベクトルから生成する場合

データフレームを複数のベクトルから生成する場合、文字列のベクトルがFactor型(因子型)になってしまう。

> name <- c("John", "Alice", "Dick")
> age <- c(35, 28, 42)
> data <- data.frame(name=name, age=age)
> str(data)
'data.frame':   3 obs. of  2 variables:
 $ name: Factor w/ 3 levels "Alice","Dick",..: 3 1 2
 $ age : num  35 28 42

> name <- c("John", "Alice", "Dick")

> age <- c(35, 28, 42)

> data <- data.frame(name=name, age=age)

> str(data)

'data.frame': 3 obs. of 2 variables:

$ name: Factor w/ 3 levels "Alice","Dick",..: 3 1 2

$ age : num 35 28 42

これを文字型に直すのに、以下の3つの方法がある。

as.charactor()関数

as.charactor()関数で指定した列がcharacter化されるので、それを元の列に代入。

> data$name <- as.character(data$name)
> str(data$name)
 chr [1:3] "John" "Alice" "Dick"

> data$name <- as.character(data$name)

> str(data$name)

chr [1:3] "John" "Alice" "Dick"

levels()関数

仕組みはよくわかっていない。

> data$name <- levels(data$name)[data$name]
> str(data$name)
 chr [1:3] "John" "Alice" "Dick"

> data$name <- levels(data$name)[data$name]

> str(data$name)

chr [1:3] "John" "Alice" "Dick"

transform()関数

データフレーム全体に適用。

> data <- transform(data, name=levels(name)[name])
> str(data$name)
 chr [1:3] "John" "Alice" "Dick"

> data <- transform(data, name=levels(name)[name])

> str(data$name)

chr [1:3] "John" "Alice" "Dick"

ファイルから読み込む場合

ファイルから読み込んだ後に上記の操作を行ってもよいが、読み込み時にFactor型への変換を抑止するため、引数にstringsAsFactors = Fを指定する方法もある。

個の引数指定は、read.table、read.delim、read.csvの何れでも指定できる。

> data <- read.csv("data/demo-dataframe1.csv", stringsAsFactors=F)
> str(data$name)
 chr [1:5] "John" "Gene" "Jack" "Luice" "Elen"

> data <- read.csv("data/demo-dataframe1.csv", stringsAsFactors=F)

> str(data$name)

chr [1:5] "John" "Gene" "Jack" "Luice" "Elen"

R – データフレームの生成

2016-09-15 / tau / コメントする

ベクトル列から生成する方法

同じ長さのベクトルを各列として、データフレームを生成可能。

name.data <- c("John", "Gene", "Jack", "Luice", "Elen")
gender.data <- c("M", "F", "M", "M", "F")
height.data <- c(165, 160, 170, 178, 157)
weight.data <- c(62, 56, 75, 82, 58)
qualified.data <- c(T, F, T, F, T)

data <- data.frame(
  name=name.data,
  gender=gender.data,
  height=height.data,
  weight=weight.data,
  qualified=qualified.data
)

data

name.data <- c("John", "Gene", "Jack", "Luice", "Elen")

gender.data <- c("M", "F", "M", "M", "F")

height.data <- c(165, 160, 170, 178, 157)

weight.data <- c(62, 56, 75, 82, 58)

qualified.data <- c(T, F, T, F, T)

data <- data.frame(

name=name.data,

gender=gender.data,

height=height.data,

weight=weight.data,

qualified=qualified.data

)

data

上記の結果は以下の通り。

> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

ファイルからの読み込み

通常、作業ディレクトリかその下にあるディレクトリにあるファイルを扱う。扱いやすいのはタブ区切りテキスト、CSV。

read.tableによる方法

TAB区切り／ヘッダなし

John	M	165	62	T
Gene	F	160	56	F
Jack	M	170	75	T
Luice	M	178	82	F
Elen	F	157	58	T

John M 165 62 T

Gene F 160 56 F

Jack M 170 75 T

Luice M 178 82 F

Elen F 157 58 T

read.tableでそのまま読み込む。項目名はRが勝手につけてくれる。

デフォルトでTABが区切り文字になってるが、明示する場合は引数にsep="\t"を追加。

> data <- read.table("data/demo-dataframe0.txt")
> data
     V1 V2  V3 V4    V5
1  John  M 165 62  TRUE
2  Gene  F 160 56 FALSE
3  Jack  M 170 75  TRUE
4 Luice  M 178 82 FALSE
5  Elen  F 157 58  TRUE

> data <- read.table("data/demo-dataframe0.txt")

> data

V1 V2 V3 V4 V5

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

CSV／ヘッダなし

John,M,165,62,T
Gene,F,160,56,F
Jack,M,170,75,T
Luice,M,178,82,F
Elen,F,157,58,T

John,M,165,62,T

Gene,F,160,56,F

Jack,M,170,75,T

Luice,M,178,82,F

Elen,F,157,58,T

read.tableで引数にsep=","を付けて読み込む。

> data <- read.table("data/demo-dataframe0.csv", sep=",")
> data
     V1 V2  V3 V4    V5
1  John  M 165 62  TRUE
2  Gene  F 160 56 FALSE
3  Jack  M 170 75  TRUE
4 Luice  M 178 82 FALSE
5  Elen  F 157 58  TRUE

> data <- read.table("data/demo-dataframe0.csv", sep=",")

> data

V1 V2 V3 V4 V5

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

TAB区切り／ヘッダあり

name	gender	height	weight	qualified
John	M	165	62	T
Gene	F	160	56	F
Jack	M	170	75	T
Luice	M	178	82	F
Elen	F	157	58	T

name gender height weight qualified

John M 165 62 T

Gene F 160 56 F

Jack M 170 75 T

Luice M 178 82 F

Elen F 157 58 T

read.tableでheader=Tを付けて読み込む。sep="\t"を指定してもよい。

> data <- read.table("data/demo-dataframe1.txt", header=T)
> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE

> data <- read.table("data/demo-dataframe1.txt", header=T)

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

この形式の場合、wrapperクラスのread.delimでファイルのみ指定して読み込める。

> data <- read.delim("data/demo-dataframe1.txt")
> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE

> data <- read.delim("data/demo-dataframe1.txt")

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

CSV／ヘッダあり

name,gender,height,weight,qualified
John,M,165,62,T
Gene,F,160,56,F
Jack,M,170,75,T
Luice,M,178,82,F
Elen,F,157,58,T

name,gender,height,weight,qualified

John,M,165,62,T

Gene,F,160,56,F

Jack,M,170,75,T

Luice,M,178,82,F

Elen,F,157,58,T

read.tableでsep=","とheader=Tを指定して読み込む。

> data <- read.table("data/demo-dataframe1.csv", sep=",", header=T)
> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE

> data <- read.table("data/demo-dataframe1.csv", sep=",", header=T)

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

この形式の場合、wrapperクラスのread.csvでファイルのみ指定して読み込める。

> data <- read.csv("data/demo-dataframe1.csv")
> data
   name gender height weight qualified
1  John      M    165     62      TRUE
2  Gene      F    160     56     FALSE
3  Jack      M    170     75      TRUE
4 Luice      M    178     82     FALSE
5  Elen      F    157     58      TRUE

> data <- read.csv("data/demo-dataframe1.csv")

> data

name gender height weight qualified

1 John M 165 62 TRUE

2 Gene F 160 56 FALSE

3 Jack M 170 75 TRUE

4 Luice M 178 82 FALSE

5 Elen F 157 58 TRUE

注意点：Factor型への自動変換

ベクトルからの生成にしても、ファイルからの読み込みにしても、文字列のデータを持ったベクトルをデータフレームに取り込むと、自動的にFactor型(因子型)にされてしまう。

> data <- read.csv("data/demo-dataframe1.csv")
> str(data$name)
 Factor w/ 5 levels "Elen","Gene",..: 4 2 3 5 1

> data <- read.csv("data/demo-dataframe1.csv")

> str(data$name)

Factor w/ 5 levels "Elen","Gene",..: 4 2 3 5 1

これを解決するための方法は列の非因子化を参照。

数列の和と階差数列

2016-09-13 / tau / コメントする

定数数列

定数数列の和は、定数の項数倍。

(1) $\begin{equation*} \sum_{k=1}^{n} a = an \end{equation*}$

等差数列

等差数列 $a_n = a + d(n - 1)$ の和は、初項と末項の和に項数を乗じた数の1/2。

(2) $\begin{equation*} \sum_{k=1}^{n} (a + d(k-1)) = \frac{1}{2}n(a_1 + a_n) \end{equation*}$

特に、

(3) $\begin{equation*} \sum_{k=1}^{n} k = \frac{n (n + 1)}{2} \end{equation*}$

証明1

等差数列の $n$ 項目までの和を $S_n$ とすると、

(4) $\begin{eqnarray*} & & \begin{array}{rcccccccc} S_n &= &a_1 &+ &(a_1 + d) &+ &\cdots & + &a_n \\ S_n &= &a_n &+ &(a_n - d) &+ &\cdots &+ &a_1 \\ \hline 2 S_n &= &(a_1 + a_n) &+ &(a_1 + a_n) &+ &\cdots &+ &(a_1 + a_n) } \end{array} \\ \\ & & \therefore \quad S_n = \frac{1}{2} n (a_1 + a_n) \end{eqnarray*}$

証明2

式(3)を使って、

(5) $\begin{eqnarray*} \sum_{k=1}^n (a + d(k - 1)) &=& an + d \frac{n (n + 1)}{2} - dn \\ &=& \frac{1}{2} n (2a + dn + d - 2d) \\ &=& \frac{1}{2} n (a + a + d(n-1)) \\ &=& \frac{1}{2} n (a_1 + a_n) \end{eqnarray*}$

等比数列

等比数列 $a_n = a r^{n-1}$ の和は以下の通り。

(6) $\begin{equation*} \sum_{k=1}^n a r^{k-1} = a \frac{1 - r^n}{1 - r} \end{equation*}$

特に、

(7) $\begin{equation*} \sum_{k=1}^{n} r^k = r \frac{1 - r^n}{1 - r} \end{equation*}$

証明

等差数列の $n$ 項目までの和を $S_n$ とすると、

(8) $\begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} S_n& = &a &+ &a r &+ &\cdots &+ &a r^{n-1} \\ r S_n &= & & &a r &+ &\cdots &+ &a r^{n-1} &+ &a r^n \\ \hline (1 - r) S_n &= &a & & & & & & &- &a r^n \\ \end{array} \\ \\ & & \therefore \quad S_n = a \frac{1 - r^n}{1 - r} \end{eqnarray*}$

等比・等差の複合数列

等差部分と等比部分の両方を含んだ数列の部分和。

(9) $\begin{equation*} \sum_{k=1}^{n} k r^k = r \frac{1 - (n + 1) r^n + n r^{n + 1}}{(1 - r)^2} \end{equation*}$

証明1

一般的な部分和の差を用いる方法。

(10) $\begin{eqnarray*} & &\begin{array}{rrrrrrrrrrr} S_n& = &1 \cdot r^1 &+ &2 \cdot r^2 &+ &\cdots &+ &n r^n \\ r S_n &= & & &1 \cdot r^2 &+ &\cdots &+ &(n - 1) r^n &+ &n r^{n + 1} \\ \hline (1 - r) S_n &= &r &+ &r^2 &+ &\cdots &+ &r^n &- &n r^{n+1} \end{array} \\ \\ & &(1 - r) S_n = r \frac{1 - r^n}{1 - r} - n r^{n+1}\\ & & \therefore \quad S_n = r \frac{1 - r^n}{(1 - r)^2} - n \frac{r^{n+1}}{1 - r} = r \frac{1 - (n + 1) r^n + n r^{n + 1}}{(1 - r)^2} \end{eqnarray*}$

証明2

微分を用いる方法。等比数列の公式、

(11) $\begin{equation*} \sum_{k=1}^n r^k = \frac{r (1 - r^n)}{1 - r} \end{equation*}$

の両辺を $r$ で微分すると、

(12) $\begin{eqnarray*} \sum_{k=1}^n k r^{k - 1} &=& \frac{(1 - r)(1 - (n + 1) r^n) + r(1 - r^n)}{(1 - r)^2} \\ &=& \frac{1 - (n+1) r^n + n r^{n+1}}{(1 - r)^2} \end{eqnarray*}$

両辺を $r$ 倍して同じ式を得る。

べき乗の数列

∑k²

(13) $\begin{equation*} \sum_{k=1}^{n} k^2 = \frac{n(n+1)(2n+1)}{6} \end{equation*}$

証明

以下の式から出発する。

(14) $\begin{eqnarray*} \sum_{k=1}^{n} \left( (k + 1)^3 - k^3 \right) &=& (n+1)^3 - 1 \\ \sum_{k=1}^{n} \left( (k + 1)^3 - k^3 \right) &=& \sum_{k=1}^{n} (3k^2 + 3k + 1) \end{eqnarray*}$

これより、

(15) $\begin{eqnarray*} \sum_{k=1}^{n} k^2 &=& \frac{(n+1)^3 - 1}{3} - \frac{n(n+1)}{2} - \frac{n}{3} \\ &=& \frac{2n^3 + 6n^2 + 6n - 3n^2 - 3n - 2n}{6} \\ &=& \frac{n(2n^2 + 3n +1)}{6} \\ &=& \frac{n(n+1)(2n+1)}{6} \end{eqnarray*}$

∑k³

(16) $\begin{equation*} \sum_{k=1}^{n} k^3 = \frac{n^2 (n+1)^2}{4} \end{equation*}$

証明

上記と同じように、

(17) $\begin{eqnarray*} \sum_{k=1}^{n} \left( (k + 1)^4 - k^4 \right) &=& (n+1)^4 - 1 \\ \sum_{k=1}^{n} \left( (k + 1)^4 - k^4 \right) &=& \sum_{k=1}^{n} (4k^3 + 6k^2 + 4k + 1) \end{eqnarray*}$

これより、

(18) $\begin{eqnarray*} \sum_{k=1}^{n} k^3 &=& \frac{(n+1)^4 - 1}{4} - \frac{6}{4} \cdot \frac{n(n+1)(2n+1)}{6} -\frac{n(n+1)}{2} - \frac{n}{4} \\ &=& \frac{n^4 + 4n^3 + 6n^2 + 4n - 2n^3 - 3n^2 - n - 2n^2 - 2n - n}{4} \\ &=& \frac{n^4 + 2n^3 + n^2}{4} \\ &=& \frac{n^2 (n+1)^2}{4} \\ \end{eqnarray*}$

階差数列

数列 $a_n$ の階差数列が扱いやすい数列の場合。

(19) $\begin{equation*} a_{n+1} - a_n = b_n \end{equation*}$

$a_n$ の各項は、 $a_1]$ ～ $a_n$ の和をとることで以下のように得られる。

(20) $\begin{equation*} a_n = a_1 + \sum_{k=1}^{n-1} b_i \end{equation*}$

【例】

$a_n$ の階差数列が $a_n - a_{n-1} = 2n - 1$ で $a_1 = 1$ のときの数列 $a_n$ は以下のようになる

$\begin{equation*} 1 \underbrace{\quad}_{1} 2 \underbrace{\quad}_{3} 5 \underbrace{\quad}_{5} 10 \cdots \end{equation*}$

この数列の一般項は、

(21) $\begin{eqnarray*} a_n &=& a_1 + \sum_{k=1}^{n-1} (2i - 1) \\ &=& 1 + 2 \frac{(n - 1) n}{2} - (n - 1) \\ &=& n^2 - 2n + 2 \end{eqnarray*}$

上式は $n = 1$ の時も初期条件 $a_1 = 1$ を満足する。

イベント制御によるポアソン過程のシミュレーション

2016-09-12 / tau / コメントする

イベント制御による分析

時刻制御(time driven)では微小な時間間隔の間において到着イベントを確率的に発生させた。そこでは結果としての到着時間間隔の指数分布や到着数のPoisson分布は前提にはおかれていない。

イベント制御(event driven)の考え方では、ある到着があった後、次の到着までの時間間隔を指数分布に従う乱数を発生させて計算する。計算にはR言語を使う。

イベント制御の考え方の概要やその他の考え方についてはRによるポアソン過程のシミュレーションを参照。

到着イベントの時系列

ここでは、到着率はこれまでと同じλ = 1/10として、時刻t = 0からt ≤ 1000秒の間、到着の時間間隔が確率密度 $e^{- \lambda t}$ の指数分布に従うような乱数を発生させていく。

指数分布に従う乱数を生成するには逆関数法を使う。

指数分布の確率分布関数は以下の通り。

(1) $\begin{equation*} F(T \le t) = 1 - e^{- \lambda t} \end{equation*}$

一様乱数runifを与えて指数分布に従う乱数を得るには、一様乱数を分布関数の逆関数に適用すればよい。

(2) $\begin{equation*} F^{-1}(t) = - \frac{1}{\lambda}\ ln(1 - {\rm runif(1)}) \end{equation*}$

lambda <- 1/ 10

data <- c()
for (i in 1:1000) {
  r <- (1 - log(runif(1))) / lambda
  data <- c(data, r)
}

lambda <- 1/ 10

data <- c()

for (i in 1:1000) {

r <- (1 - log(runif(1))) / lambda

data <- c(data, r)

}

時刻0を起点として、1番目の到着時刻をこの指数乱数で決定し、その次の到着時刻も指数乱数で・・・と繰り返して、時刻が上限を超えるまで時系列として記録する。

interval <- function(lambda) return( (1 - log(runif(1))) / lambda )

lambda <- 1/ 10
t.obs <- 5000
rank.width <- 100

t <- 0
arrivals <- c()
while (t < t.obs) {
  arrivals <- c(arrivals, t)
  t <- t + interval(lambda)
}

hist(arrivals, breaks=seq(0, t.obs, rank.width))

interval <- function(lambda) return( (1 - log(runif(1))) / lambda )

lambda <- 1/ 10

t.obs <- 5000

rank.width <- 100

t <- 0

arrivals <- c()

while (t < t.obs) {

arrivals <- c(arrivals, t)

t <- t + interval(lambda)

}

hist(arrivals, breaks=seq(0, t.obs, rank.width))

一様乱数による場合と同じく、到着率1/10、観測時間5000秒として、階級幅100秒、500秒の場合の時系列を生成したのが下図。階級あたりのデータ数と分布の平滑さの関係は、一様乱数による場合やtime drivenの場合と同じ。

poisson-process-event-driven-arrival100

poisson-process-event-driven-arrival500

到着数の分布

到着数の確率分布は、一様乱数による場合やtime drivenと同じように集計する。

interval <- function(lambda) return( -log(1 - runif(1)) / lambda )

generate <- function(t.obs, lambda) {
  t <- 0
  data <- c()
  while (t < t.obs) {
    data <- c(data, t)
    t <- t + interval(lambda)
  }
  return (length(data))
}

lambda <- 1/ 10
t.obs <- 1000
n.loop <- 100

arrivals <- rep(0, n.loop)
for (i in 1:n.loop) arrivals[i] <- (generate(t.obs, lambda))

hist(arrivals, freq=FALSE)
curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE)

interval <- function(lambda) return( -log(1 - runif(1)) / lambda )

generate <- function(t.obs, lambda) {

t <- 0

data <- c()

while (t < t.obs) {

data <- c(data, t)

t <- t + interval(lambda)

}

return (length(data))

}

lambda <- 1/ 10

t.obs <- 1000

n.loop <- 100

arrivals <- rep(0, n.loop)

for (i in 1:n.loop) arrivals[i] <- (generate(t.obs, lambda))

hist(arrivals, freq=FALSE)

curve((lambda*t.obs)^x/factorial(x)*exp(-lambda*t.obs), add=TRUE)

結果は、Poisson分布の理論式ともよくあっている。

poisson-process-event-driven-poisson

オブジェクトの直接表示

print()～一般的な表示

page()～別ウィンドウでの表示

cat()～文字列の表示

str()～オブジェクト情報付き表示

summary()～データの要約を表示する。

考え方

定数定義

トランザクションの到着時刻の発生

サービス時間の計算

待ち行列長の推移の集計

計算結果の表示

計算結果

ρ = 0.5のケース

ρ = 0.9のケース

前提

状態方程式

定常問題化と状態方程式の解

ρの意味

平均トランザクション数と平均待ち行列長

リトルの法則(Litter’s law)

データフレーム全体の参照

データフレームの行数・列数の参照

データフレームの内容の参照・変更

列名・項目名の参照・変更

データフレームの要素の参照・変更

行・列の追加と削除

行・列の追加

行・列の削除

データの抽出

order()関数

降順ソート

複数列のソートなど

行番号の変更

ベクトルから生成する場合

as.charactor()関数

levels()関数

transform()関数

ファイルから読み込む場合

ベクトル列から生成する方法

ファイルからの読み込み

read.tableによる方法

TAB区切り／ヘッダなし

CSV／ヘッダなし

TAB区切り／ヘッダあり

CSV／ヘッダあり

注意点：Factor型への自動変換

定数数列

等差数列

証明1

証明2

等比数列

証明

等比・等差の複合数列

証明1

証明2

べき乗の数列

∑k2

証明

∑k3

証明

階差数列

イベント制御による分析

到着イベントの時系列

到着数の分布

関連リンク

∑k²

∑k³