Bernoulli試行の成功確率をpとする。この試行をn回繰り返す場合の二項分布に従う確率変数X(成功回数)の平均と分散は以下で表される。
(1) ![]()
試行回数nが大きいとき、中心極限定理より以下の確率変数は標準正規分布に従う。
(2) ![]()
分母・分子をnで割り、サンプルから観測された確率として![]() と置く。
と置く。
(3) 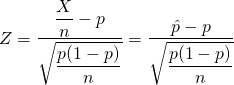
Zが標準正規分布に従うことから、信頼確率αの信頼区間は以下のように表せる。
(4) 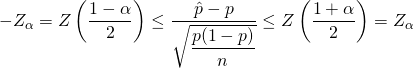
これよりpの信頼区間は以下のように表せる。
(5) ![]()
ここで信頼区間の境界値の計算に母比率pが含まれているが、nが大きいときは![]() として、以下を得る。
として、以下を得る。
(6) ![]()
ここで、母比率0~1.0のBernoulli試行を繰り返し数を変えて試行したときの観測確率について、その平均と標準偏差がどうなるか計算してみた。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
import numpy as np import scipy.stats as stats import pandas as pd def p_trials(n, p, m): sum_p = [] for traial in range(m): x = stats.uniform.rvs(size=n) sum_p.append(len(x[x<p]) / n) return np.mean(sum_p), np.std(sum_p, ddof=1) np.random.seed(0) p_list = np.arange(0, 1.1, 0.1) n_list = [10, 20, 30, 50, 100, 1000] n_trials = 100 mean_results = np.empty((len(p_list), len(n_list))) std_results = np.empty((len(p_list), len(n_list))) for cp, p in enumerate(p_list): for cn, n in enumerate(n_list): mean, std = p_trials(n, p, n_trials) mean_results[cp, cn] = mean std_results[cp, cn] = std pd.options.display.precision = 3 df_mean = pd.DataFrame(mean_results, columns=n_list) df_mean["p"] = p_list columns = ["p"] + n_list df_mean = df_mean.loc[:, columns] df_std = pd.DataFrame(std_results, columns=n_list) df_std["p"] = p_list columns = ["p"] + n_list df_std = df_std.loc[:, columns] print(df_mean) print(df_std) |
まずpの平均についてはn = 10でもそれなりの精度となっていて、あまり試行回数による変化は大きくない。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
p 10 20 30 50 100 1000 0 0.0 0.000 0.000 0.000 0.000 0.000 0.000 1 0.1 0.093 0.102 0.105 0.099 0.097 0.101 2 0.2 0.215 0.194 0.196 0.208 0.206 0.203 3 0.3 0.328 0.287 0.295 0.297 0.299 0.299 4 0.4 0.393 0.384 0.394 0.396 0.407 0.399 5 0.5 0.494 0.491 0.514 0.494 0.497 0.498 6 0.6 0.596 0.609 0.605 0.592 0.598 0.600 7 0.7 0.695 0.714 0.704 0.698 0.694 0.700 8 0.8 0.811 0.807 0.799 0.791 0.793 0.798 9 0.9 0.910 0.904 0.887 0.898 0.903 0.902 10 1.0 1.000 1.000 1.000 1.000 1.000 1.000 |
次にpの標準偏差(不偏分散の平方根)を見てみる。母比率が1/2に近いほどばらつきは大きく、試行回数nが大きいほどばらつきは小さくなっている。実務的にはn = 50~100あたりでそれなりのばらつきで観測確率をを母比率の代わりに用いてよいだろうか。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
p 10 20 30 50 100 1000 0 0.0 0.000 0.000 0.000 0.000 0.000 0.000 1 0.1 0.090 0.067 0.061 0.041 0.029 0.010 2 0.2 0.120 0.092 0.083 0.053 0.038 0.011 3 0.3 0.162 0.103 0.090 0.068 0.043 0.013 4 0.4 0.145 0.110 0.079 0.074 0.049 0.016 5 0.5 0.148 0.105 0.094 0.060 0.048 0.016 6 0.6 0.150 0.124 0.102 0.069 0.047 0.016 7 0.7 0.127 0.106 0.084 0.060 0.042 0.015 8 0.8 0.117 0.098 0.065 0.052 0.036 0.012 9 0.9 0.089 0.060 0.056 0.043 0.030 0.010 10 1.0 0.000 0.000 0.000 0.000 0.000 0.000 |
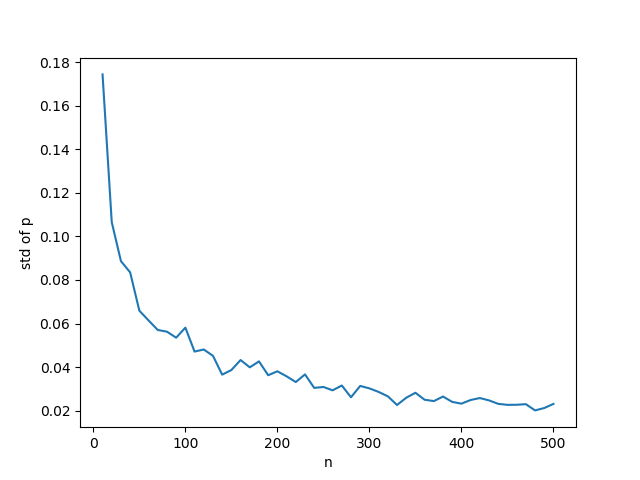
以下はB(n, 0.5)についてnを変化させたときの観測確率のグラフで、やはりn = 50あたりまでにばらつきが急に減っていることがわかる。