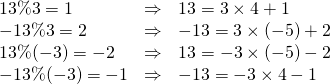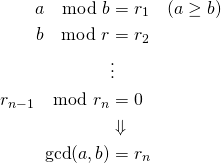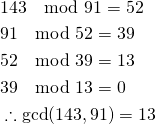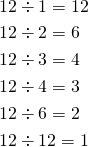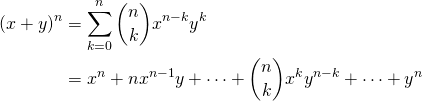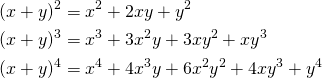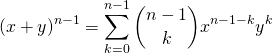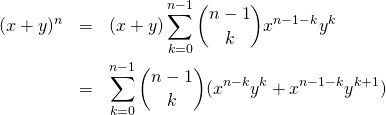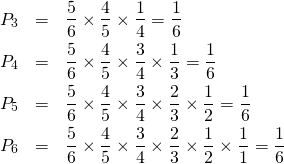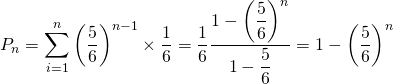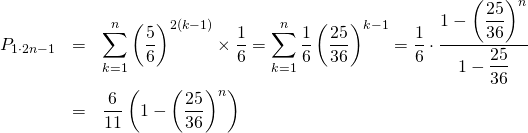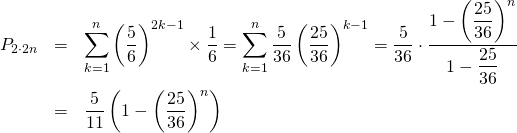Python3 – 書式設定～format

2019-07-27 / tau / コメントする

format関数

一つの数値・文字列の書式を設定する場合、format組み込み関数が使える。引数はリテラルでも変数でもよい。

print("Hexadecimal of 255 is " + format(255, '0x'))
print("1/7 is approximately " + format(1/7, 'e'))


# Hexadecimal of 255 is ff
# 1/7 is approximately 1.428571e-01

print("Hexadecimal of 255 is " + format(255, '0x'))

print("1/7 is approximately " + format(1/7, 'e'))

# Hexadecimal of 255 is ff

# 1/7 is approximately 1.428571e-01

formatメソッド

文字列に対するformatメソッドでも数値・文字列の書式を設定できる（書式設定の書き方は後述）。引数はリテラルでも変数でもよい。

print("Hexadecimal of 255 is {:0x}".format(255))
print("Hexadecimal of 255 is {:e}".format(1/7))

# Hexadecimal of 255 is ff
# Hexadecimal of 255 is 1.428571e-01

print("Hexadecimal of 255 is {:0x}".format(255))

print("Hexadecimal of 255 is {:e}".format(1/7))

# Hexadecimal of 255 is ff

# Hexadecimal of 255 is 1.428571e-01

formatメソッドは複数の数値・文字列を扱える。

print("My name is {} and my age is {}".format("Jane", 38))

# My name is Jane and my age is 38

print("My name is {} and my age is {}".format("Jane", 38))

# My name is Jane and my age is 38

位置引数として整数を指定し、繰り返して利用することが可能。

print("The suits of handed cards were {0}, {1}, {2}, {1}, {3}" \
    .format("Spade", "Club", "Diamond", "Heart".))

# The suits of handed cards were Spade, Club, Diamond, Club, Heart.

print("The suits of handed cards were {0}, {1}, {2}, {1}, {3}" \

.format("Spade", "Club", "Diamond", "Heart".))

# The suits of handed cards were Spade, Club, Diamond, Club, Heart.

キーワード引数として文字列を指定可能。

print("{name} is {age} years old.".format(name="Kark", age=25))

# Kark is 25 years old.

print("{name} is {age} years old.".format(name="Kark", age=25))

# Kark is 25 years old.

リストを引数にするときは整数の位置引数とリスト内の引数で指定する。複数のリストを指定するときは位置引数を0、1…と対応させていく。

result1 = ["Head", "Tail"]
result2 = ["Head", "Head"]
print("First result was {0[0]} and {0[1]}.\nSecond was {1[0]} and {1[1]}.".\
    format(result1, result2))

# First result was Head and Tail.
# Second was Head and Head.

result1 = ["Head", "Tail"]

result2 = ["Head", "Head"]

print("First result was {0[0]} and {0[1]}.\nSecond was {1[0]} and {1[1]}.".\

format(result1, result2))

# First result was Head and Tail.

# Second was Head and Head.

辞書を引数にするときは整数の位置引数とキーで指定する。キーはクォートで囲まない。

person1 = {'name': "John", 'age': 20}
person2 = {'name': "Kate", 'age': 32}
print("{0[name]} is {0[age]} years old) and {1[name]} is {1[age]} years old.".\
    format(person1, person2))

# John is 20 years old) and Kate is 32 years old.

person1 = {'name': "John", 'age': 20}

person2 = {'name': "Kate", 'age': 32}

print("{0[name]} is {0[age]} years old) and {1[name]} is {1[age]} years old.".\

format(person1, person2))

# John is 20 years old) and Kate is 32 years old.

書式設定する場合は、[位置引数]:[書式設定文字列]の形式にする。位置引数を指定しない場合でも':'は必要。

print("1/4 is {0:f} and 1/5 is {1:e}".format(1/4, 1/5))
print("1/4 is {:f} and 1/5 is {:e}".format(1/4, 1/5))

# 1/4 is 0.250000 and 1/5 is 2.000000e-01
# 1/4 is 0.250000 and 1/5 is 2.000000e-01

print("1/4 is {0:f} and 1/5 is {1:e}".format(1/4, 1/5))

print("1/4 is {:f} and 1/5 is {:e}".format(1/4, 1/5))

# 1/4 is 0.250000 and 1/5 is 2.000000e-01

書式設定文字列

formatメソッド

位置引数を省略して書式設定文字列を各場合{:[書式設定文字列]}のように':'を省略することができない。

文字列

{:[</^/>][width]}で左寄せ／中央ぞろえ／右寄せと、全体の幅widthを指定。

str = "Python"

print("left  :{:<10}".format(str))
print("center:{:^10}".format(str))
print("right :{:>10}".format(str))

# left  :Python
# center:  Python
# right :    Python

str = "Python"

print("left :{:<10}".format(str))

print("center:{:^10}".format(str))

print("right :{:>10}".format(str))

# left :Python

# center: Python

# right : Python

{:[char][</^/>][width]}で空白部分をcharの文字でパディング

print("left  :{:*<10}".format(str))
print("center:{:*^10}".format(str))
print("right :{:*>10}".format(str))

# left  :Python****
# center:**Python**
# right :****Python

print("left :{:*<10}".format(str))

print("center:{:*^10}".format(str))

print("right :{:*>10}".format(str))

# left :Python****

# center:**Python**

# right :****Python

整数

整数の書式は幅の値に'd'を続けて書く。

print("{:*<10d}".format(123))
print("{:*^10d}".format(123))
print("{:*>10d}".format(123))

# 123*******
# ***123****
# *******123

print("{:*<10d}".format(123))

print("{:*^10d}".format(123))

print("{:*>10d}".format(123))

# 123*******

# ***123****

# *******123

整数を2進数、8進数、16進数で表現できる。

print("{:d}".format(255))
print("{:b}".format(255))
print("{:o}".format(255))
print("{:x}".format(255))
print("{:X}".format(255))

# 255
# 11111111
# 377
# ff
# FF

print("{:d}".format(255))

print("{:b}".format(255))

print("{:o}".format(255))

print("{:x}".format(255))

print("{:X}".format(255))

# 255

# 11111111

# 377

# ff

# FF

基数を指定するとき、'#'を前置すると0b、0o、0xが前に付加される。以下の例では、同時に幅も指定している。2進数表現の場合は0bを付加すると設定幅を超えるので、そのまま表示されている。

print("{:#8b}".format(255))
print("{:#8o}".format(255))
print("{:#8x}".format(255))
print("{:#8X}".format(255))

# 0b11111111
#    0o377
#     0xff
#     0XFF

print("{:#8b}".format(255))

print("{:#8o}".format(255))

print("{:#8x}".format(255))

print("{:#8X}".format(255))

# 0b11111111

# 0o377

# 0xff

# 0XFF

浮動小数点

浮動小数点形式の実数の書式は、小数部の桁数だけ指定するときは".3f"のように、幅を設定するときは"10.3f"のように指定する。

print("{:*<10.3f}".format(12.3454))
print("{:*^10.3f}".format(12.3455))
print("{:*>10.3f}".format(12.3456))

# 12.345****
# **12.345**
# ****12.346

print("{:*<10.3f}".format(12.3454))

print("{:*^10.3f}".format(12.3455))

print("{:*>10.3f}".format(12.3456))

# 12.345****

# **12.345**

# ****12.346

固定小数点

固定小数点形式の実数の書式は、小数部の桁数だけ指定するときは".5e"のように、幅を指定するときは"15.5e"のように指定する。

# 固定小数点型
print("{:*<15.3e}".format(1.2344e-10))
print("{:*^15.3e}".format(1.2345e-10))
print("{:*>15.3e}".format(1.2346e-10))

# 1.234e-10******
# ***1.234e-10***
# ******1.235e-10

# 固定小数点型

print("{:*<15.3e}".format(1.2344e-10))

print("{:*^15.3e}".format(1.2345e-10))

print("{:*>15.3e}".format(1.2346e-10))

# 1.234e-10******

# ***1.234e-10***

# ******1.235e-10

符号の表示方法

正の数値に対して'+'を表示させるときは、数値書式の前に'+'をつけ、正の時にスペースを表示させるときには' 'をつける。

print("{:*>10d}".format(123))
print("{:*>10d}".format(-123))
print("{:*>+10d}".format(123))
print("{:*>+10d}".format(-123))
print("{:*> 10d}".format(123))
print("{:*> 10d}".format(-123))

# *******123
# ******-123
# ******+123
# ******-123
# ****** 123
# ******-123

print("{:*>10d}".format(123))

print("{:*>10d}".format(-123))

print("{:*>+10d}".format(123))

print("{:*>+10d}".format(-123))

print("{:*> 10d}".format(123))

print("{:*> 10d}".format(-123))

# *******123

# ******-123

# ******+123

# ******-123

# ****** 123

# ******-123

指定した幅の先頭に符号等を表示し、右寄せの数値との間をパディングする方法。

print("{:*=10.3f}".format(12.345))
print("{:*=10.3f}".format(-12.345))
print("{:*=+10.3f}".format(12.345))
print("{:*= 10.3f}".format(12.345))

# ****12.345
# -***12.345
# +***12.345
#  ***12.345

print("{:*=10.3f}".format(12.345))

print("{:*=10.3f}".format(-12.345))

print("{:*=+10.3f}".format(12.345))

print("{:*= 10.3f}".format(12.345))

# ****12.345

# -***12.345

# +***12.345

# ***12.345

format関数

基数表示

数値の基数を指定して、10進数、2進数、8進数、16進数を表示。16進数は英文字の大文字/小文字を選択可能。

print(format(255, 'd')) #255
print(format(255, 'b')) #11111111
print(format(255, 'o')) #377
print(format(255, 'x')) #ff
print(format(255, 'X')) #FF

print(format(255, 'd')) #255

print(format(255, 'b')) #11111111

print(format(255, 'o')) #377

print(format(255, 'x')) #ff

print(format(255, 'X')) #FF

位置揃え

文字列や数値を固定幅の中で左寄せ、センタリング、右寄せ（センタリングで左右幅が異なるときは、左に1桁寄せられる）。

print(format("Python", '<10s')) #Python
print(format("Python", '^10s')) #  Python
print(format("Python", '>10s')) #    Python

print(format(123, '<6d'))   #123
print(format(123, '^6d'))   # 123
print(format(123, '>6d'))   #   123

print(format("Python", '<10s')) #Python

print(format("Python", '^10s')) # Python

print(format("Python", '>10s')) # Python

print(format(123, '<6d')) #123

print(format(123, '^6d')) # 123

print(format(123, '>6d')) # 123

パディング

数値を固定幅で表示した場合のデフォルトは右寄せ。'[任意の文字]=’で空白をパディング。特にゼロで埋める場合は’=’を省略できる。

print(format(123, '6d'))    #   123
print(format(123, '*=6d'))  #***123
print(format(123, '0=6d'))  #000123
print(format(123, '06d'))   #000123

print(format(123, '6d')) # 123

print(format(123, '*=6d')) #***123

print(format(123, '0=6d')) #000123

print(format(123, '06d')) #000123

2、8、16の基数に対して固定幅で0でパディングする例。

print(format(15, '08b'))    #00001111
print(format(15, '04o'))    #0017
print(format(143, '04x'))   #008f
print(format(143, '04X'))   #008F

print(format(15, '08b')) #00001111

print(format(15, '04o')) #0017

print(format(143, '04x')) #008f

print(format(143, '04X')) #008F

+符号

‘+’を指定すると、正の値の時に+記号がつく。

print(format(456, '+6d'))   #  +456
print(format(-456, '+6d'))  #  -456
print(format(-456, '+06d')) #-00456
# '0+6d'はエラー

print(format(456, '+6d')) # +456

print(format(-456, '+6d')) # -456

print(format(-456, '+06d')) #-00456

# '0+6d'はエラー

カンマ区切り

3桁ごとのカンマ区切り指定。

print(format(123456789, ','))   #123,456,789
print(format(123456789, '15,')) #    123,456,789

1 2	print(format(123456789, ',')) #123,456,789 print(format(123456789, '15,')) # 123,456,789

固定小数点実数

固定小数点の小数部の桁数を’.[桁数]f’で指定する。

print(format(123.456789, '.3f'))  #123.457
print(format(123.456789, '.10f')) #123.4567890000

1 2	print(format(123.456789, '.3f')) #123.457 print(format(123.456789, '.10f')) #123.4567890000

浮動小数点実数

浮動小数点の小数部の桁数を’.[桁数]e’で指定する。

print(format(123.456, '.0e'))   #1.e+02
print(format(123.456, '.1e'))   #1.2e+02
print(format(123.456, '.2e'))   #1.23e+02
print(format(123.456, '.3e'))   #1.235e+02

print(format(123.456, '.0e')) #1.e+02

print(format(123.456, '.1e')) #1.2e+02

print(format(123.456, '.2e')) #1.23e+02

print(format(123.456, '.3e')) #1.235e+02

実数全体の桁数

小数部の桁数ではなく全体の桁数を’.[桁数]g’で指定する。全体の桁数が整数部の桁数以上のときは、固定小数点で表示される。

print(format(123.456, '.0g'))   #1e+02
print(format(123.456, '.1g'))   #1e+02
print(format(123.456, '.2g'))   #1.2e+02
print(format(123.456, '.3g'))   #123
print(format(123.456, '.4g'))   #123.5
print(format(123.456, '.5g'))   #123.46

print(format(123.456, '.0g')) #1e+02

print(format(123.456, '.1g')) #1e+02

print(format(123.456, '.2g')) #1.2e+02

print(format(123.456, '.3g')) #123

print(format(123.456, '.4g')) #123.5

print(format(123.456, '.5g')) #123.46

Python3 – 整数除算と剰余（//, %）

2019-07-22 / tau / 1件のコメント

//演算子

//演算子は、切り捨て除算と言われることが多いが、正確には小数部の切り捨てではなく、除算値を超えない最大の整数となる。これは実数の除算結果にfloorを適用した値と同じで、除算結果が負の時に注意を要する。

import math

print(8/3)
print(8//3)
print(math.floor(8/3))

# 2.6666666666666665
# 2
# 2

print(-7/3)
print(-7//3)
print(math.floor(-7/3))

# -2.3333333333333335
# -3
# -3

import math

print(8/3)

print(8//3)

print(math.floor(8/3))

# 2.6666666666666665

# 2

print(-7/3)

print(-7//3)

print(math.floor(-7/3))

# -2.3333333333333335

# -3

なお、被除数・除数の何れがマイナスかは問わず、計算結果がマイナスかどうかだけによる。

%演算子

%演算子は、引数の剰余(mod)を与える。除数の正負によって挙動が異なる点に注意。

print(13%3)     # 1
print(-13%3)    # 2
print(13%(-3))  # -2
print(-13%(-3)) # -1

print(13%3) # 1

print(-13%3) # 2

print(13%(-3)) # -2

print(-13%(-3)) # -1

除数が正のとき剰余は正となり、除数が負のときは剰余は負となる。

$\begin{array}{lcl} 13 \% 3 = 1 & \Rightarrow & 13 = 3 \times 4 + 1 \\ -13 \% 3 = 2 & \Rightarrow & -13 = 3 \times (-5) + 2 \\ 13 \% (-3) = -2 & \Rightarrow & 13 = -3 \times (-5) - 2 \\ -13 \% (-3) = -1 & \Rightarrow & -13 = -3 \times 4 -1 \end{array}$

Python3 – 組み込み関数

2019-07-21 / tau / コメントする

range関数

zip関数

map関数

Python3 – range関数

2019-07-21 / tau / コメントする

概要

Python3のrange関数は引数で指定した範囲の整数列をrangeオブジェクトで返す。rangeオブジェクトを表示するには、list関数でリスト化する必要がある。

>>> range(0, 5)
range(0, 5)
>>> list(range(0, 5))
[0, 1, 2, 3, 4]

>>> range(0, 5)

range(0, 5)

>>> list(range(0, 5))

[0, 1, 2, 3, 4]

書式

range(end): 0から始まり、1ずつ増加してendに達しない範囲の数列
range(start, end): startから始まり、1ずつ増加してendに達しない範囲の数列
range(start, end, step): startから始まり、stepずつ増加してendに達しない範囲の数列

引数は整数である必要があり、そうでなければエラーとなる。

共通なのは、開始値からステップ値ずつ変化させ、終了値に達する直前までの数列を返す、というもので、ステップ値が正の場合にはstart ≤ 値 < endを、ステップ値が負の場合にはstart ≥ 値 > endを要素とする数列となる。

実行例

引数を1つだけ指定した場合は、0から引数未満の整数列となる。

>>> list(range(10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

1 2	>>> list(range(10)) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

引数を2つ指定すると、第1引数以上、第2引数未満の整数列となる。

>>> list(range(3, 10))
[3, 4, 5, 6, 7, 8, 9]

1 2	>>> list(range(3, 10)) [3, 4, 5, 6, 7, 8, 9]

引数を3つ指定すると、第1引数から第3引数ずつ増加して第2引数を超える手前までの整数列となる。

>>> list(range(0, 10, 3))
[0, 3, 6, 9]

1 2	>>> list(range(0, 10, 3)) [0, 3, 6, 9]

第3引数を負の数とすると、降順の数列になる。このとき、第2引数の終了値以下になる前までの数列となっていることに注意。

>>> list(range(10, 0, -1))
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
>>> list(range(10, 0, -4))
[10, 6, 2]

>>> list(range(10, 0, -1))

[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]

>>> list(range(10, 0, -4))

[10, 6, 2]

なお、2つだけ引数を指定して、第1引数＞第2引数としても、降順の数列は得られず、空となる。

>>> list(range(10, 0))
[]

1 2	>>> list(range(10, 0)) []

ユークリッドの互除法

2019-07-15 / tau / コメントする

概要

ユークリッドの互除法(Euclidean Algorithm)は、2つの自然数の最大公約数を求める手順。

2つの自然数 $a, b \; (a \ge b)$ の最大公約数(GCD: greatest common divisor)は、 $b$ と剰余 $r = a \mod b$ の最大公約数に等しいという性質を利用。数を順次割り込んでいき、剰余がゼロとなったときの除数が最大公約数となる。

(1) $}\begin{align*}a \mod b &= r_1 \quad (a \ge b) \\b \mod r &= r_2 \\&\vdots \\r_{n-1} \mod r_n &= 0 \\&\Downarrow \\\gcd(a, b) &= r_n\end{align*}$

証明

以下の余りあり除算を考える。

(2) $\begin{gather*}a \mod b = r \Rightarrow a = bd + r\end{gather*}$

$a, b$ の公約数を $m$ とすると、上式は以下のように変形され、 $m$ は $b$ と $r$ の公約数でもあることがわかる。

(3) $\begin{gather*}a = mp , \quad b = mq \\r = mp - mqd = m(p - qd)\end{gather*}$

一方、 $b, r$ の公約数を $n$ とすると、 $n$ は $a$ と $b$ の公約数であることがわかる。

(4) $\begin{gather*}b = ns , \quad r = nt \\a = nsd + nt = n(sd + t)\end{gather*}$

これより、 $a, b$ の公約数の集合と $b, r$ の公約数の集合は等しく、最大公約数も等しくなる。

(5) $\begin{equation*}a = bd+r \Rightarrow \gcd(a, b) = \gcd(b, r)\end{equation*}$

計算例

143と91の最大公約数を求める。

(6) $\begin{align*}&143 \mod 91 = 52 \\&91 \mod 52 = 39 \\&52 \mod 39 = 13 \\&39 \mod 13 = 0 \\&\therefore \gcd(143, 91) = 13\end{align*}$

再帰関数による実装

PythonとCLispの再帰関数による実装例は以下の通り。ただし、第1引数>第2引数を前提としており、エラー処理はしていない。

Python

def gcd(a, b):
	if a % b == 0:
		return b
	else:
		return gcd(b, a % b)

print( gcd(12, 8) )

def gcd(a, b):

if a % b == 0:

return b

else:

return gcd(b, a % b)

print( gcd(12, 8) )

CLisp

(defun mygcd (a b)
	(if (= (mod a b) 0) b (mygcd b (mod a b)))
)

(print (mygcd 18 12))

(defun mygcd (a b)

(if (= (mod a b) 0) b (mygcd b (mod a b)))

)

(print (mygcd 18 12))

最大公約数・最小公倍数

2019-07-13 / tau / コメントする

約数

約数の定義

整数 $N$ の約数(divisor, factor)とは、Nを割り切る整数(余りが生じない除数)。

整数 $m$ が $N$ の約数であるとき、 $m|N$ と表し、ある整数 $a$ に対して $N=ma$ が成り立つことでもある。一般には自然数あるいは0以上の整数で考える。

通常は $m \ne 0$ の条件を課すが、0も含める場合は、 $N=0$ の時に限り0が約数になる。

例えば12の約数は、以下の6個。

(1) $\begin{align*}&12 \div 1 = 12 \\&12 \div 2 = 6 \\&12 \div 3 = 4 \\&12 \div 4 = 3 \\&12 \div 6 =2 \\&12 \div 12 = 1\end{align*}$

効率的な約数の求め方

$m|N$ であるとき、 $\frac Nm|N$ である。これより $m = \frac Nm$ として、 $\sqrt N$ 以下の約数 $m_i$ を求め、あとは $N/m_i$ を計算すれば、手間が半分で済む。

$N$ が平方数の場合は $\sqrt N$ も約数となり、約数の総数は奇数個、平方数でない場合は偶数異なる。

0、1の約数

0の約数は $0 = ma$ となる整数 $m$ であり、0以上の全ての整数である。

1の約数は $1 = ma$ となる整数 $m$ であり、1のみ。

1は全ての整数の約数。

素数の約数

素数の定義が「1と自身以外に約数を持たない数」なので、約数は2個。

公約数

2つの数の公約数は、それらの最大公約数の約数。

0、1との公約数

$a$ と1の公約数は1のみ。

$a$ と0の公約数は、 $a$ の約数全て(0の約数は0以上の全ての整数)。

公約数と剰余

$a \mod b = r$ のとき、 $a, b$ の公約数は $b, r$ の公約数でもある。

最大公約数

2つの数の最大公約数(greatest common divisor)を、 $\gcd(a, b)$ のように表す。

最大公約数を求める手順として、にユークリッドの互除法がある。

0、1との最大公約数

(2) $\begin{gather*}\gcd(a, 0) = a \\\gcd(a, 1) = 1\end{gather*}$

最大公約数と剰余

被除数と除数の最大公約数は、除数と剰余の最大公約数でもある。

(3) $\begin{equation*}a \mod b = r \Rightarrow \gcd(a, b) = \gcd(b, r)\end{equation*}$

倍数

倍数(multiple)とは、ある数 $a$ (整数に限らない)を整数倍した数である。

(4) $\begin{gather*}\cdots \; -3a,\; -2a,\; -a,\; 0,\; a,\; 2a,\; 3a,\; \cdots\end{gather*}$

0の倍数は0のみ
0はすべての数の倍数
すべての数は自分自身の倍数
すべての整数は1と-1の倍数

最小公倍数

最小公倍数(least common multiple)とは、2つの整数の公倍数のうち、正で最小のもの。

たとえば36と56の最小公倍数は504。

最大公約数と最小公倍数の積

2つの数 $a, b$ の積は、それらの最大公約数と最小公倍数の積に等しい。

(5) $\begin{equation*}ab = \gcd(a, b) \cdot \operatorname{lcm}(a, b)\end{equation*}$

Python3 – mathモジュール

2019-07-13 / tau / コメントする

使い方

数学関数を使うためのモジュールで、importし、各定数・関数について、math.[定数名・関数名]として使う。

>>> import math
>>> math.sqrt(2)
1.4142135623730951

>>> import math

>>> math.sqrt(2)

1.4142135623730951

関数群

主なもの

定数

pi, e: 円周率、自然対数の底
inf: 浮動小数点の正の無限大。負の無限大は-math.inf。
nan: 浮動小数点の非数NaN。

数論関数

ceil(x): xの天井(x以上の最小の整数)。
floor(x): xの床(x以下の最大の整数)。
fabs(x): xの絶対値。
fmod(x, y): $x \mod y$ を返す。浮動小数点の場合はx % yよりこちらを使う。
gcd(x, y): xとyの最大公約数。gcd(0.0, 0.0)は0を返す。
isfinite(x): xが無限でもNaNでもない時にTrueを返す。
ifinf(x): xが正の無限大か負の無限大の時にTrueを返す。
isnan(x): xがNaNの時にTrueを返す。

指数・対数関数

sqrt(n): nの平方根
pow(x, y): xのy乗( $x^y$ )。pow(1.0, x)、pow(x, 0.0)は常に1.0を返す。
exp(x): $e^x$ 。
expm1(n): $e^x - 1$ 。桁落ちに対して最大精度で計算。
log2(x), log10(x), log(x [,b]): それぞれ2、10、bを底とする対数関数。3番目の関数でbを省略した場合は自然対数 $\ln x$
log1p(x): $1+\log x$

を返す。ゼロに近いxに対して正確になるよう計算される。

三角関数

sin(x), cos(x), tan(x): 三角関数。
asin(x), acos(x), atan(x): 逆三角関数
atan2(y, x): [latex]\tan^{^1}を返すが、4つの象限に対する符号から、[latex]-\pi \sim \pi[/lates]の値を返す。
degrees(r), radians(d): ラジアンから度、度からラジアンへの変換。

剰余と合同式

2019-07-10 / tau / コメントする

商と剰余

剰余(余り)について

$a \div b$ の商が $q$ 、余りが $r$ のとき、以下のように表される。d:divisor、q:quotient、r:reminderの意味。

(1) $\begin{eqnarray*} &a = dq + r \\ &a \mod d = r \end{eqnarray*}$

余りの定義を「割る数未満の自然数あるいは0」とすると、

(2) $\begin{eqnarray*} 8 &=& 3 \times 2 + 2 \\ 7 &=& 3 \times 2 + 1 \\ 6 &=& 3 \times 2 + 0 \\ 5 &=& 2 \times 2 + 2 \\ 4 &=& 2 \times 2 + 1 \\ 3 &=& 2 \times 2 + 0 \end{eqnarray*}$

割られる数が負の場合には、

(3) $\begin{eqnarray*} -9 &=& 3 \times (-3) + 0 \\ -8 &=& 3 \times (-3) + 1 \\ -7 &=& 3 \times (-3) + 2 \\ -6 &=& 3 \times (-2) + 0 \\ -5 &=& 3 \times (-2) + 1 \\ -4 &=& 3 \times (-2) + 2 \end{eqnarray*}$

割る数が負の場合には、

(4) $\begin{eqnarray*} 9 &=& -3 \times (-3) + 0 \\ 8 &=& -3 \times (-3) + 1 \\ 7 &=& -3 \times (-3) + 2 \\ 6 &=& -3 \times (-2) + 0 \\ 5 &=& -3 \times (-2) + 1 \\ 4 &=& -3 \times (-2) + 2 \\ \end{eqnarray*}$

負数の余り

余りとして負の数を認めることもできる。ただしその場合、商と余りの組み合わせが1つとは限らない。

(5) $\begin{eqnarray*} 10 &=& -3 \times (-3) + 1 \\ 10 &=& -3 \times (-4) -2 \end{eqnarray*}$

余りの定義(要件)は以下の2通りがあり、いずれを採用するかは任意。

余りを割る数の絶対値より小さい0以上とする $(0 \le r < |d|)$
余りの絶対値が割る数の絶対値より小さい数とする $(0 \le |r| < |d|)$

特別な場合の余り

割る数が1あるいは-1のときは、余りは常に0。

(6) $\begin{eqnarray*} a &=& 1 \times a + 0 \\ a &=& -1 \times (-a) + 0 \end{eqnarray*}$

割られる数が1のときの余りは1、割られる数が-1なら余りは割る数の絶対値から1を現じた値(余りを正と定義した場合)。

(7) $\begin{eqnarray*} 1 &=& b \times 0 + 1 \\ -1 &=& b \times 1 + b - 1 \quad (b > 0) \\ -1 &=& b \times (-1)1 + (-b - 1) \quad (b < 0) \end{eqnarray*}$

合同式

合同式の定義

整数 $a, b$ を正の整数 $d$ で割った余りが等しいとき、以下のように表記し、「 $a, b$ は $d$ を法として合同である」という。

(8) $\begin{eqnarray*} a &\equiv& b \mod{d}\\ a &\equiv& b \pmod d \end{eqnarray*}$

これは次のようにも表現できる。

(9) $\begin{equation*} a - pd = b - qd = r \end{equation*}$

合同式の例

(10) $\begin{eqnarray*} 7 &\equiv& 4 \bmod 3\\ 6 &\equiv& 4 \bmod 2\\ 6 &\equiv& 0 \bmod 2\\ 5 &\equiv& 1 \bmod 2 \\ 5 &\equiv& (-1) \bmod 3 \end{eqnarray*}$

角度の例

以下の例では、330度と−30度が合同となっている。360度回転するたびに元の位置に戻るイメージ。

(11) $\begin{eqnarray*} 1050 &\equiv& 690 \bmod 360 \\ 690 &\equiv& 330 \bmod 360 \\ 330 &\equiv& -30 \bmod 360 \\ -30 &\equiv& -390 \bmod 360 \end{eqnarray*}$

合同式の性質

以下、合同式の $\mod d$ を省略する。

合同式の和

(12) $\begin{equation*} a_1 \equiv b_1 , \; a_2\equiv b_2 \; \Rightarrow \; a_1 + a_2 \equiv b_1 + b_2 \end{equation*}$

【証明】

$\begin{eqnarray} a_1 - p_1 d &=& b_1 - q_1 d \\ a_2 - p_2 d &=& b_2 - q_2 d \\ &\Downarrow& \\ (a_1 + a_2) - (p_1 + p_2)d &=& (b_1 + b_2) - (q_1 + q_2) d$

合同式の積

(13) $\begin{equation*} a_1 \equiv b_1 , \; a_2\equiv b_2 \; \Rightarrow \; a_1 a_2 \equiv b_1 b_2 \end{equation*}$

【証明】

(14) $\begin{eqnarray*} a_1 - p_1 d &=& b_1 - q_1 d \\ a_2 - p_2 d &=& b_2 - q_2 d \\ &\Downarrow& \\ (a_1 - p_1 d)(a_2 - p_2 d) &=& (b_1 - q_1 d)(b_2 - q_2 d) \\ &\Downarrow& \\ a_1 a_2 - (a_1 p_2 + a_2 p_1 + p_1 p_2 d) d &=& b_1 b_2 - (b_1 q_2 + b_2 q_1 + q_1 q_2 d) d \end{eqnarray*}$

合同式の商

$a, \; d$ が互いに素 $(a \perp d)$ のとき、以下が成り立つ。

(15) $\begin{equation*} ab \equiv ac \bmod d \; \Rightarrow \; b \equiv c \bmod d \quad ( {\rm where} \; a \perp d ) \end{equation*}$

【証明】

(16) $\begin{eqnarray*} ab \equiv ac \bmod d \; &\Rightarrow& \; ab = dp + r , \; ac = dq + r \\ &\Rightarrow& a(b - c) = d(p + q) \\ \end{eqnarray*}$

ここで $a, \; b$ は互いに素なので、 $b-c$ が $d$ の倍数となる。

(17) $\begin{eqnarray*} b - c = dk &\Rightarrow& \; b = dm + s , \; ac = dn + s \\ &\Rightarrow& b \equiv c \bmod d \\ \end{eqnarray*}$

合同式の冪乗

(18) $\begin{equation*} a \equiv b \bmod d \; \Rightarrow \; a^n \equiv b^n \bmod d \end{equation*}$

【証明】

(19) $\begin{equation*} a \equiv b \bmod d \quad \Leftrightarrow \quad \left\{ \begin{array}{l} a = pd + r \\ b = qd + r \end{array} \right. \end{equation*}$

(20) $\begin{eqnarray*} a^n &=& (pd + r)^n = \sum_{k=0}^n \dbinom{n-k}{k} (pd)^{n-k} r^k \\ &=& pd \sum_{k=0}^{n-1} \dbinom{n-k}{k} (pd)^{n-k-1} r^k + r^n \\ b^n &=& (qd + r)^n = \sum_{k=0}^n \dbinom{n-k}{k} (qd)^{n-k} r^k \\ &=& qd \sum_{k=0}^{n-1} \dbinom{n-k}{k} (qd)^{n-k-1} r^k + r^n \end{array} \end{eqnarray*}$

二項定理

2019-07-10 / tau / コメントする

二項定理の表現

(1) $\begin{align*} (x + y)^n &= \sum_{k=0}^n \binom{n}{k} x^{n-k} y^k \\ &= x^n + n x^{n-1}y + \cdots + \binom{n}{k} x^k y^{n-k} + \cdots + y^n \end{align*}$

具体例

(2) $\begin{align*} (x + y)^2 &= x^2 + 2xy + y^2 \\ (x + y)^3 &= x^3 + 3x^2 y +3x y^2 + x y^3 \\ (x + y)^4 &= x^4 + 4x^3 y + 6x^2 y^2 + 4x y^3 + y^4 \end{align*}$

証明

数学的帰納法で証明する。

$n = 0$ のとき、

(3) $\begin{equation*} (x + y)^0 = \binom 00 x^0 y^0 = 1 \end{equation*}$

$n = 1$ のとき、

(4) $\begin{equation*} (x + y)^1 = \binom 10 x^1 y^0 + \binom 11 x^0 y^1 = x + y \end{equation*}$

ここで $n-1$ のときに以下が成り立つとする。

(5) $\begin{equation*} (x + y)^{n-1} = \sum_{k=0}^{n-1} \binom{n-1}{k} x^{n-1-k} y^k \end{equation*}$

このとき $n$ に関しては、

(6) $\begin{eqnarray*} (x + y)^n &=& (x + y) \sum_{k=0}^{n-1} \binom {n-1}{k} x^{n-1-k} y^k \\ &=& \sum_{k=0}^{n-1} \binom {n-1}{k} (x^{n-k} y^k + x^{n-1-k} y^{k+1}) \end{eqnarray*}$

これを右辺は以下のように展開できる。

$\begin{array}{rrrrrrrrrrrrrrr} & x^n & + & (n-1) x^{n-1} y & \cdots & \binom{n-1}{k} x^{n-k} y^k & \cdots & x y^{n-1} \\ + &&& x^{n-1} y & \cdots & \binom{n-1}{k-1} x^{n-k} y^k &\cdots & (n-1) x y^{n-1} & + & y^n \\ \hline & x^n & + & n x^{n-1} y & \cdots & \left( \binom{n-1}{k} - \binom{n-1}{k-1}\right) x^{n-k}{k} & \cdots & n x y^{n-1} & + & y^n \\ \end{array} \\$

(7) $\begin{eqnarray*} \binom{n-1}{k} - \binom{n-1}{k-1} &=& \frac{(n-1)!}{(n-k-1)! k!} - \frac{(n-1)!}{(n-k)! (k-1)!} \\ &=& (n-1)! \frac{(n-k) - k}{(n-k)! k!} = \binom nk \end{eqnarray*}$

これより、 $n \ge 0$ に対して(1)が証明された。

パスカルの三角形

数のような数による三角形をパスカルの三角形(Pascal’s triangle)と呼び、n行目の数の列が二項展開のn乗の係数となっている。

各項の計算の仕方は、一つ上の段の左右の数の和として求めていく（左端・右端の外側はゼロと考える）。

pascals-triangle

パスカルの三角形の各項が二項展開の計数となること、すなわちm段目のn項目の数を $a_{m \cdot n}$ とし、これが $\binom{m-1}{n-1}$ となることを、数学的帰納法で証明する。

(8) $\begin{eqnarray*} a_{2 \cdot 1} &=& \binom{1}{0} = 1 \\ a_{2 \cdot 2} &=& \binom{1}{1} = 1 \end{eqnarray*}$

(9) $\begin{eqnarray*} a_{m \cdot n} &=& a_{m-1 \cdot n-1} + a_{m-1 \cdot n} = \binom{m-2}{n-2} + \binom{m-2}{n-1} \\ &=& \frac{(m-2)!}{(m-n)!(n-2)!} + \frac{(m-2)!}{(m-n-1)!(n-1)!} \\ &=& (m-2)! \frac{(n-1) + (m-n)}{(m-n)!(n-1)!} = \frac{(m-1)!}{(m-n)!(n-1)!} \\ &=& \binom{m-1}{n-1} \end{eqnarray*}$

ロシアンルーレットの確率

2019-07-04 / tau / コメントする

基本

ロシアンルーレットは、賭の順番問題や条件付き確率の問題としてよく見かける。まず、一番基本的なルールで考える。

1人の相手とロシアンルーレットで命をかけることになった。6発入りの拳銃に1発だけ弾を込め、最初にシリンダーを高速で回転させる。シリンダーが止まったところで、相手と交互に引き金を引いていくとして、まず自分から始めるのと相手に譲るのと、どちらが生き残る可能性が高いか。

n回目に実弾に当たる確率を $P_n \; (n = 1~6)$ とすると、

1発目で当たる確率は、6つの弾倉のどこかに実弾が入っているので、

(1) $\begin{equation*} P_1 = \frac{1}{6} \end{equation*}$

2発目で当たる確率は、1発目で実弾に当たらず、2発目は残り5つの弾倉のどこかに実弾が入っているので、

(2) $\begin{equation*} P_2 = \frac{5}{6} \times \frac{1}{5} = \frac{1}{6} \end{equation*}$

以下、6発目まで同じように考えて、

(3) $\begin{eqnarray*} P_3 &=& \frac{5}{6} \times \frac{4}{5} \times \frac{1}{4} = \frac{1}{6} \\ P_4 &=& \frac{5}{6} \times \frac{4}{5} \times \frac{3}{4} \times \frac{1}{3} = \frac{1}{6} \\ P_5 &=& \frac{5}{6} \times \frac{4}{5} \times \frac{3}{4} \times \frac{2}{3} \times \frac{1}{2} = \frac{1}{6} \\ P_6 &=& \frac{5}{6} \times \frac{4}{5} \times \frac{3}{4} \times \frac{2}{3} \times \frac{1}{2} \times \frac{1}{1}= \frac{1}{6} \end{eqnarray*}$

すなわち、通常のロシアンルーレットでは、1～6回目のどこで実弾に当たる確率も等しく1/6で、順番の後先に有利性はない。

毎回シリンダーを回転させる場合

1発だけ弾を込めた拳銃で、2人でロシアンルーレットで命をかける。ただし、それぞれが自分の番になる毎にシリンダーを回転させて、ランダムに止まったところで引き金を引く。自分が最初に打つのと、相手から打たせるのと、どちらを選ぶか。

毎回シリンダーを回転させるので、そこまで発砲されていなければ、実弾である確率は毎回1/6。 $n$ 回目に実弾に当たる確率を $p_n$ とすると、 $n-1$ 回は当たらないことを考慮して、

(4) $\begin{equation*} p_n = \left( \frac{5}{6} \right) ^{n-1} \times \frac{1}{6} \end{equation*}$

まず、この確率はnが大きくなるほどゼロに近づく。たとえば1回めで当たる確率は約16.7%、10回目で当たる確率は約3.2%、20回目で当たる確率は0.5%、40回目だと約0.01%程度となる。

次に、 $n$ 回目までに当たる確率を $P_n$ とすると、これは各回の確率を累積していくことで求められるので、等比数列の和より、

(5) $\begin{equation*} P_n = \sum_{i=1}^{n} \left( \frac{5}{6} \right) ^{n-1} \times \frac{1}{6} = \frac{1}{6} \frac{1-\left( \dfrac{5}{6} \right)^n}{1 - \dfrac{5}{6}} = 1-\left( \dfrac{5}{6} \right)^n \end{equation*}$

この累積確率は $n \rightarrow \infty$ のとき1に近づくが、10回目で約83.8%、20回目で約97.4%、30回目で約99.6%、40回目で約99.9%となり、100回も打ってその時点で生き延びている確率はほとんどゼロに近い。

次に交互に打っていく場合を考える。

先攻で打つ方になった場合、1回目、3回目・・・と奇数回に打つことになるので、その累積確率を $P_{1 \cdot n}$ とすると、

(6) $\begin{eqnarray*} P_{1\cdot 2n-1} &=& \sum_{k=1}^{n} \left( \frac{5}{6} \right)^{2(k-1)} \times \frac{1}{6} = \sum_{k=1}^{n} \frac{1}{6} \left( \frac{25}{36} \right)^{k-1} = \frac{1}{6} \cdot \frac{1 - \left( \dfrac{25}{36}\right) ^n }{1 - \dfrac{25}{36}} \\ &=& \frac{6}{11} \left( 1 - \left( \dfrac{25}{36}\right) ^n \right) \end{eqnarray*}$

後攻で打つ方になった場合は、2回目、4回目・・・と偶数回に打つことになるので、その累積確率を $P_{2 \cdot n}$ とすると、

(7) $\begin{eqnarray*} P_{2\cdot 2n} &=& \sum_{k=1}^{n} \left( \frac{5}{6} \right)^{2k-1} \times \frac{1}{6} = \sum_{k=1}^{n} \frac{5}{36} \left( \frac{25}{36} \right)^{k-1} = \frac{5}{36} \cdot \frac{1 - \left( \dfrac{25}{36}\right) ^n }{1 - \dfrac{25}{36}} \\ &=& \frac{5}{11} \left( 1 - \left( \dfrac{25}{36}\right) ^n \right) \end{eqnarray*}$

同じ $n$ に対して常に $P_{1 \cdot n} / P_{2 \cdot n} = 1.2$ となり、先に打つのを選んだほうが実弾に当たる確率は高く、この比率は $n \rightarrow \infty$ としたときの結果と同じ。

したがって、「お先にどうぞ」と相手に最初を譲ったほうが、少しでも生き残る確率が高くなる。また、3人以上で順番に打っていく場合は、できるだけ後の順番で打つ方が実弾に当たる確率が低くなる。

条件付きの問題

2発の弾を並べて込める

ロシアンルーレットと少し違うが、条件付きの問題。

筋悪の金貸しから借りたかなりの借金を返せなくなり、命を取られようとしているが、「チャンスをやる」と言われた。彼は6発入りの拳銃の弾倉に2 発の弾を並べて込め、シリンダーを回す。シリンダーがランダムな位置で止まったところで、彼は言う。「今から空に向かって私が1回引き金を引く。その後にお前のこめかみに銃口を当てて打ってもらうが、そのまま打ってもいいし、もう一度シリンダーを回して止まった位置で打ってもいい」

1発目が空砲の場合

金貸しが銃を空に向けて引き金を引くと空砲だった。そのまま打つか、シリンダーを回転させるか、どちらを選択すべきか。

まず、シリンダーをもう一度回転させてから打つ場合は、6弾倉中2発残っているので、当たる確率は1/3。逆に助かる率は2/3となる。

一方シリンダーを回転させない場合は、手渡された拳銃の弾の状態を、円形に並んだ弾倉を一列で表し、下表のように整理する。ただし、左欄の●は実弾がある場所、○は実弾が入っていない場所で、1番目は金貸しが打ったときの位置、2番目は手渡された時の位置。右欄は2発目が実弾の場合は●、空砲の場合は○とする。

●●○○○○	対象外
○●●○○○	●
○○●●○○	○
○○○●●○	○
○○○○●●	○
●○○○○●	対象外

金貸しが打ったときは空砲だったので、1番目が実弾の事象は対象外。このとき、実弾に当たらない確率は3/4となる。

すなわち、もう一度シリンダーを回転させるよりも、そのまま続けて打った方が助かる可能性が高い。

1発目が実弾の場合

もし、金貸しが最初に空へ向けて打ったときに実弾だった場合はどうか？

この場合に続けて打つと、1発目が実弾である2ケースに対して、空砲で助かる率は1/2。

シリンダーを回転させてから打つと、実弾は残り1発なので、当たらない確率は5/6で、回転させて打った方が生存確率は高くなる。

条件に応じた選択と確率

以上の結果を整理すると下表の通りとなり、1発目が空砲の場合と実弾の場合で、その後の選択による生存確率の高い方が逆転している。

空砲も実弾もその位置が連続しているため、1発目が空砲の場合は続けて空砲の確率が高く、1発目が実弾の場合は次も実弾の確率が高そうだが、1発目が実弾の場合は弾が1つ消費されるので、その影響で結果が逆転している。

1発目	選択	生存確率
空砲	シリンダー回転	1/3 (0.33)
空砲	続けて打つ	3/4 (0.75)
実弾	シリンダー回転	5/6 (0.83)
実弾	続けて打つ	1/2 (0.50)

実弾2発をランダムに込める

上記の金貸しの問題では実弾2発を並べて込めたが、これをランダムな位置に2発込めた場合はどうなるか。

この場合、2発の実弾の装填状況は下表のようになる。

1発目が→	空砲	実弾
●●○○○○	対象外	●
●○●○○○	対象外	○
○●●○○○	●	対象外
●○○●○○	対象外	○
○●○●○○	●	対象外
○○●●○○	○	対象外
●○○○●○	対象外	○
○●○○●○	●	対象外
○○●○●○	○	対象外
○○○●●○	○	対象外
●○○○○●	対象外	○
○●○○○●	●	対象外
○○●○○●	○	対象外
○○○●○●	○	対象外
○○○○●●	○	対象外

1発目が空砲だった場合

シリンダーを回転させた場合の生存確率は、4/6 = 2/3 (0.667)。

続けて打つ場合は、1発目が実弾のケースを除いて2発目が空砲の場合なので、6/10 = 3/5 (0.6)。

1発目が実弾だった場合

シリンダーを回転させた場合の生存確率は、5/6 (0.833)。

続けて打つ場合は、1発目が空砲のケースを除いて2発目が空砲の場合なので、4/5 (0.8)。

1発目が空砲でも実弾でも、シリンダーを回転させた方が生き残る確率が高くなる。