相加相乗平均の不等式
一般系
(1) ![Rendered by QuickLaTeX.com \begin{equation*} a_i \ge 0 \quad \Rightarrow \quad \sum_{i=1}^{n} a_i \ge n \sqrt[n]{\prod_{i=1}^{n} a_i} \end{equation*}](http://taustation.com/wp1/wp-content/ql-cache/quicklatex.com-7316e733b885728513bce2577cd689f4_l3.png)
2項の場合
(2) ![]()
コーシー・シュワルツの不等式
(3) 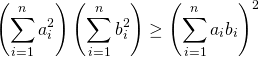
2項の場合
(4) ![]()
直線![]() 、点
、点![]() の距離を考える。直線と各点の記号、座標を以下のように定義する。
の距離を考える。直線と各点の記号、座標を以下のように定義する。
(1) ![]()
まず、ベクトル![]() が直線
が直線![]() に直交することを示す。直線は以下のように媒介変数表示できて、ベクトル
に直交することを示す。直線は以下のように媒介変数表示できて、ベクトル![]() は直線に平行なベクトル。
は直線に平行なベクトル。
(2) ![]()
これを直線の式に代入して、
(3) ![]()
ここで任意の![]() に対して上式が成り立つことから、
に対して上式が成り立つことから、![]() となり、ベクトル
となり、ベクトル![]() は直線に垂直であることが示された。
は直線に垂直であることが示された。
別解:点と直線の距離をパラメーター(媒介変数)によって愚直に求める方法
与えられた点![]() から直線
から直線![]() への垂線の足を
への垂線の足を![]() とすると、
とすると、![]() なので、以下が成り立つ。
なので、以下が成り立つ。
(4) ![]()
ここで![]() は直線
は直線![]() 上にあることを考慮し、上式の左辺を以下のように変形できる。
上にあることを考慮し、上式の左辺を以下のように変形できる。
(5) 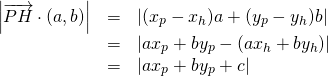
これより
(6) ![]()
3次元空間内の平面は、たとえば以下のように表すことができる。
(7) ![]()
一方、3次元平面上の点と法線ベクトル![]() との直行条件から、以下のようにも表現できる。
との直行条件から、以下のようにも表現できる。
(8) 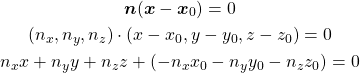
上記2つの式より、ベクトル![]() は平面に対する法線ベクトルであることがわかる。
は平面に対する法線ベクトルであることがわかる。
この法線ベクトルがベクトル![]() と平行であることから、
と平行であることから、
(9) ![]()
上式の左辺は以下のように変形できる。
(10) 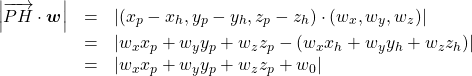
以上のことから、点![]() から三次元平面
から三次元平面![]() への距離については、以下で表される。
への距離については、以下で表される。
(11) ![]()
n次元の超平面を以下の式で与える。
(12) ![]()
このとき、これまでと同様の考え方により、点![]() と上記の超平面との距離は以下で表される。
と上記の超平面との距離は以下で表される。
(13) ![]()
ベクトルはnp.array()で引数にリストを指定して定義。
|
1 2 3 4 |
v = np.array([1, 2, 3]) print(v) # [1 2 3] |
行列は同じくnp.array()で引数に二次元配列のリストを指定して定義。
|
1 2 3 4 5 |
m = np.array([[1, 2, 3], [4, 5, 6]]) print(m) # [[1 2 3] # [4 5 6]] |
numpy.identity(n)でn×nの単位行列を生成。
|
1 2 3 4 5 6 |
print(np.identity(4)) # [[1. 0. 0. 0.] # [0. 1. 0. 0.] # [0. 0. 1. 0.] # [0. 0. 0. 1.]] |
行列の転置にはtranspose()メソッドを使う。代替として.Tとしてもよい。
|
1 2 3 4 5 6 7 8 9 10 |
m = np.array([[1, 2, 3], [4, 5, 6]]) print(m.transpose()) print(m.T) # [[1 4] # [2 5] # [3 6]] # [[1 4] # [2 5] # [3 6]] |
一次元配列で定義したベクトルにはtranspose()は効かない。列ベクトルに変換するにはreshape()メソッドを使う(reshape(行数, 列数))。
|
1 2 3 4 5 6 7 8 |
v = np.array([1, 2, 3]) print(v.T) print(v.reshape(3, 1)) # [1 2 3] # [[1] # [2] # [3]] |
ベクトル・行列の定数倍は、各要素の定数倍。
|
1 2 3 4 5 6 7 8 9 10 |
a = 2 v = np.array([1, 2, 3]) m = np.array([[1, 2, 3], [4, 5, 6]]) print(a*v) print(a*m) # [2 4 6] # [[ 2 4 6] # [ 8 10 12]] |
同じ要素数のベクトル、同じ次元の行列同士の下限は要素同士の加減
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
a = np.array([1, 2, 3]) b = np.array([2, 4, 6]) A = np.array([[1, 2], [3, 4]]) B = np.array([[2, 4], [6, 8]]) print(a + b) print(a - b) print(A + B) print(A - B) # [3 6 9] # [-1 -2 -3] # [[ 3 6] # [ 9 12]] # [[-1 -2] # [-3 -4]] |
同じ要素数のベクトルの内積(ドット積)はnp.dot()で計算。
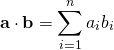
|
1 2 3 4 5 |
a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) print(np.dot(a, b)) # 32 |
*演算子を使うと、要素ごとの積になる。
|
1 2 3 |
print(a*b) # [ 4 10 18] |
行列同士の積もnp.dot()で計算。l×m行列とm×n行列の積はl×n行列になる。
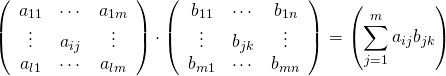
|
1 2 3 4 5 6 7 8 9 |
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4], [5, 6]]) print(np.dot(A, B)) # [[22 28] # [49 64]] |
次元数が整合しないとエラーになる。
|
1 2 3 4 5 6 7 |
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4]]) print(np.dot(A, B)) # ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0) |
行ベクトルと行列の積は、ベクトルを前からかけてok。
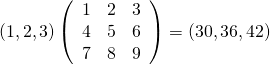
|
1 2 3 4 5 6 7 |
a = np.array([1, 2, 3]) A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(np.dot(a, A)) # [30 36 42] |
行列と列ベクトルの積は、一次元配列のベクトルをreshape()で列ベクトルに変換してから。
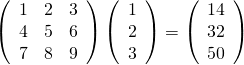
|
1 2 3 4 5 6 7 8 9 |
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) a = np.array([1, 2, 3]).reshape(3, 1) print(np.dot(A, a)) # [[14] # [32] # [50]] |
なお、np.dot()の代わりに演算子@が使える。ベクトル同士なら内積、少なくともいずれか一つが行列なら行列積。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
a = np.array([1, 2]) b = np.array([1, 2, 3]).reshape(3, 1) A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.array([[1, 2], [3, 4], [5, 6]]) print(a @ a) print(a @ A) print(A @ b) print(A @ B) # 5 # [ 9 12 15] # [[14] # [32]] # [[22 28] # [49 64]] |
行列式はnumpy.linalgパッケージのdet()関数で得られる。linalgは”linear algebra”の略で、慣例としてLAという名前で代替される。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy.linalg as LA A = np.array([[1, 2], [3, 4]]) B = np.array([[1, 2, 3], [2, 1, 3], [3, 1, 2]]) print(LA.det(A)) print(LA.det(B)) # -2.0000000000000004 # 6.000000000000001 |
逆行列はnumpy.linalgパッケージのinv()関数で得られる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
A = np.array([[1, 2], [3, 4]]) B = np.array([[1, 2, 3], [2, 1, 3], [3, 1, 2]]) print(LA.inv(A)) print(LA.inv(B)) # [[-2. 1. ] # [ 1.5 -0.5]] # [[-0.16666667 -0.16666667 0.5 ] # [ 0.83333333 -1.16666667 0.5 ] # [-0.16666667 0.83333333 -0.5 ]] |
正方行列の固有値と固有ベクトルを、eig()関数で得ることができる(行列の固有値・固有ベクトルの例題を用いた)。
|
1 2 3 4 5 6 |
A = np.array([[3, 1], [2, 4]]) print(LA.eig(A)) # (array([2., 5.]), array([[-0.70710678, -0.4472136 ], # [ 0.70710678, -0.89442719]])) |
結果は固有値が並んだベクトルと固有ベクトルが並んだ配列で、それぞれを取り出して利用する。なお、固有ベクトルはノルムが1となるように正規化されている。
|
1 2 3 4 5 6 7 |
eigenvalues, eigenvectors = LA.eig(A) print(eigenvalues) print(eigenvectors) # [2. 5.] # [[-0.70710678 -0.4472136 ] # [ 0.70710678 -0.89442719]] |
注意が必要なのは固有ベクトルの方で、各固有ベクトルは配列の列ベクトルとして並んでいる。固有ベクトルを取り出す方法は2通り。
固有値に対応するサフィックスで列ベクトルを取り出す。この方法はnumpyの公式ドキュメントにも以下のように書かれている。
|
1 2 3 |
print(eigenvectors[:,0], eigenvectors[:,1]) # [-0.70710678 0.70710678] [-0.4472136 -0.89442719] |
固有ベクトルの配列を転置して、行ベクトルの並びにする。
|
1 2 3 4 |
eigenvectors = eigenvectors.T print(eigenvectors[0], eigenvectors[1]) # [-0.70710678 0.70710678] [-0.4472136 -0.89442719] |
行列![]() の固有値・固有ベクトルは以下で定義される。
の固有値・固有ベクトルは以下で定義される。
(1) ![]()
これを以下のように変形する。
(2) ![]()
この方程式が解をもつためには、以下の条件が必要。
(3) ![]()
以下の行列に対する固有値、固有ベクトルを求める。
(4) ![]()
この行列に対する固有値方程式は以下の通り。
(5) ![]()
これを解くと、
(6) 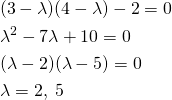
次に、各固有値に対する固有ベクトルを求める。
まず![]() に対しては、
に対しては、
(7) 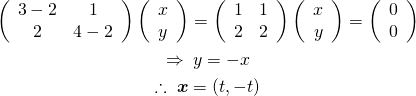
確認してみると、
(8) ![]()
また![]() に対しては、
に対しては、
(9) 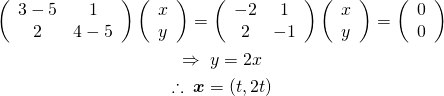
こちらも確認してみると、
(10) ![]()
なお、固有ベクトルを数値で表現する際、ノルムが1となるように正規化することが多い。
(11) ![]()
上の例で固有値ベクトルを正規化すると以下の通り。
(12) 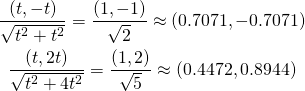
ユークリッドの互除法(Euclidean Algorithm)は、2つの自然数の最大公約数を求める手順。
2つの自然数![]() の最大公約数(GCD: greatest common divisor)は、
の最大公約数(GCD: greatest common divisor)は、![]() と剰余
と剰余![]() の最大公約数に等しいという性質を利用。数を順次割り込んでいき、剰余がゼロとなったときの除数が最大公約数となる。
の最大公約数に等しいという性質を利用。数を順次割り込んでいき、剰余がゼロとなったときの除数が最大公約数となる。
(1) 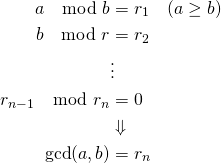
以下の余りあり除算を考える。
(2) ![]()
![]() の公約数を
の公約数を![]() とすると、上式は以下のように変形され、
とすると、上式は以下のように変形され、![]() は
は![]() と
と![]() の公約数でもあることがわかる。
の公約数でもあることがわかる。
(3) ![]()
一方、![]() の公約数を
の公約数を![]() とすると、
とすると、![]() は
は![]() と
と![]() の公約数であることがわかる。
の公約数であることがわかる。
(4) ![]()
これより、![]() の公約数の集合と
の公約数の集合と![]() の公約数の集合は等しく、最大公約数も等しくなる。
の公約数の集合は等しく、最大公約数も等しくなる。
(5) ![]()
143と91の最大公約数を求める。
(6) 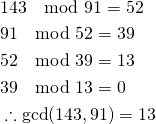
PythonとCLispの再帰関数による実装例は以下の通り。ただし、第1引数>第2引数を前提としており、エラー処理はしていない。
Python
|
1 2 3 4 5 6 7 |
def gcd(a, b): if a % b == 0: return b else: return gcd(b, a % b) print( gcd(12, 8) ) |
CLisp
|
1 2 3 4 5 |
(defun mygcd (a b) (if (= (mod a b) 0) b (mygcd b (mod a b))) ) (print (mygcd 18 12)) |
整数![]() の約数(divisor, factor)とは、Nを割り切る整数(余りが生じない除数)。
の約数(divisor, factor)とは、Nを割り切る整数(余りが生じない除数)。
整数![]() が
が![]() の約数であるとき、
の約数であるとき、![]() と表し、ある整数
と表し、ある整数![]() に対して
に対して![]() が成り立つことでもある。一般には自然数あるいは0以上の整数で考える。
が成り立つことでもある。一般には自然数あるいは0以上の整数で考える。
通常は![]() の条件を課すが、0も含める場合は、
の条件を課すが、0も含める場合は、![]() の時に限り0が約数になる。
の時に限り0が約数になる。
例えば12の約数は、以下の6個。
(1) 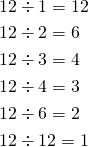
![]() であるとき、
であるとき、![]() である。これより
である。これより![]() として、
として、![]() 以下の約数
以下の約数![]() を求め、あとは
を求め、あとは![]() を計算すれば、手間が半分で済む。
を計算すれば、手間が半分で済む。
![]() が平方数の場合は
が平方数の場合は![]() も約数となり、約数の総数は奇数個、平方数でない場合は偶数異なる。
も約数となり、約数の総数は奇数個、平方数でない場合は偶数異なる。
0の約数は![]() となる整数
となる整数![]() であり、0以上の全ての整数である。
であり、0以上の全ての整数である。
1の約数は![]() となる整数
となる整数![]() であり、1のみ。
であり、1のみ。
1は全ての整数の約数。
素数の定義が「1と自身以外に約数を持たない数」なので、約数は2個。
2つの数の公約数は、それらの最大公約数の約数。
![]() と1の公約数は1のみ。
と1の公約数は1のみ。
![]() と0の公約数は、
と0の公約数は、![]() の約数全て(0の約数は0以上の全ての整数)。
の約数全て(0の約数は0以上の全ての整数)。
![]() のとき、
のとき、![]() の公約数は
の公約数は![]() の公約数でもある。
の公約数でもある。
2つの数の最大公約数(greatest common divisor)を、![]() のように表す。
のように表す。
最大公約数を求める手順として、にユークリッドの互除法がある。
(2) ![]()
被除数と除数の最大公約数は、除数と剰余の最大公約数でもある。
(3) ![]()
倍数(multiple)とは、ある数![]() (整数に限らない)を整数倍した数である。
(整数に限らない)を整数倍した数である。
(4) ![]()
最小公倍数(least common multiple)とは、2つの整数の公倍数のうち、正で最小のもの。
たとえば36と56の最小公倍数は504。
2つの数![]() の積は、それらの最大公約数と最小公倍数の積に等しい。
の積は、それらの最大公約数と最小公倍数の積に等しい。
(5) ![]()
![]() の商が
の商が![]() 、余りが
、余りが![]() のとき、以下のように表される。d:divisor、q:quotient、r:reminderの意味。
のとき、以下のように表される。d:divisor、q:quotient、r:reminderの意味。
(1) ![]()
余りの定義を「割る数未満の自然数あるいは0」とすると、
(2) 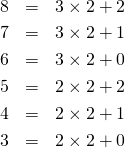
割られる数が負の場合には、
(3) 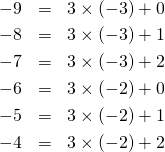
割る数が負の場合には、
(4) 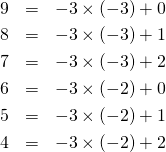
余りとして負の数を認めることもできる。ただしその場合、商と余りの組み合わせが1つとは限らない。
(5) ![]()
余りの定義(要件)は以下の2通りがあり、いずれを採用するかは任意。
割る数が1あるいは-1のときは、余りは常に0。
(6) ![]()
割られる数が1のときの余りは1、割られる数が-1なら余りは割る数の絶対値から1を現じた値(余りを正と定義した場合)。
(7) 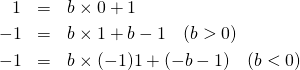
整数![]() を正の整数
を正の整数![]() で割った余りが等しいとき、以下のように表記し、「
で割った余りが等しいとき、以下のように表記し、「![]() は
は![]() を法として合同である」という。
を法として合同である」という。
(8) ![]()
これは次のようにも表現できる。
(9) ![]()
(10) 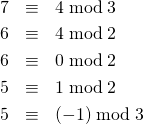
以下の例では、330度と−30度が合同となっている。360度回転するたびに元の位置に戻るイメージ。
(11) 
以下、合同式の![]() を省略する。
を省略する。
(12) ![]()
【証明】
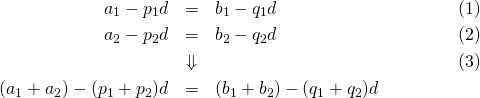
(13) ![]()
【証明】
(14) 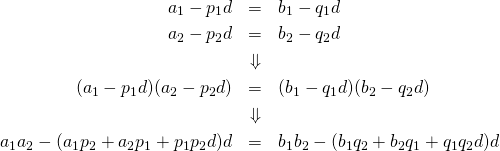
![]() が互いに素
が互いに素![]() のとき、以下が成り立つ。
のとき、以下が成り立つ。
(15) ![]()
【証明】
(16) ![]()
ここで![]() は互いに素なので、
は互いに素なので、![]() が
が![]() の倍数となる。
の倍数となる。
(17) ![]()
(18) ![]()
【証明】
(19) ![]()
(20) 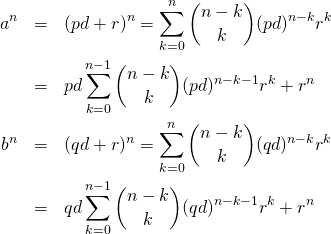
(1) 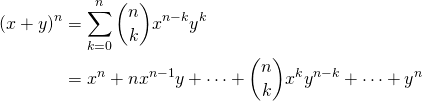
(2) 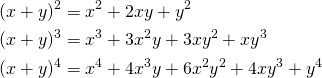
数学的帰納法で証明する。
![]() のとき、
のとき、
(3) ![]()
![]() のとき、
のとき、
(4) ![]()
ここで![]() のときに以下が成り立つとする。
のときに以下が成り立つとする。
(5) 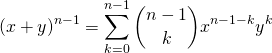
このとき![]() に関しては、
に関しては、
(6) 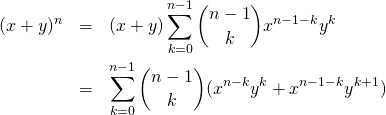
これを右辺は以下のように展開できる。
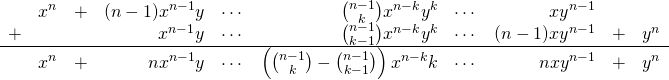
(7) 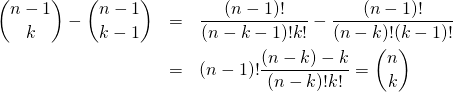
これより、![]() に対して(1)が証明された。
に対して(1)が証明された。
数のような数による三角形をパスカルの三角形(Pascal’s triangle)と呼び、n行目の数の列が二項展開のn乗の係数となっている。
各項の計算の仕方は、一つ上の段の左右の数の和として求めていく(左端・右端の外側はゼロと考える)。

パスカルの三角形の各項が二項展開の計数となること、すなわちm段目のn項目の数を![]() とし、これが
とし、これが![]() となることを、数学的帰納法で証明する。
となることを、数学的帰納法で証明する。
(8) 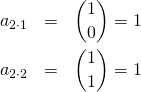
(9) 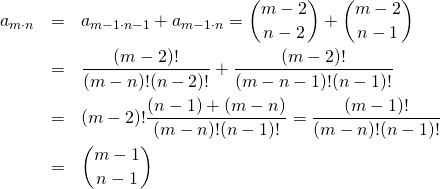
初等的な微分の定義は以下の通り。
(1) ![]()
(2) ![]()
(3) ![]()
ここで
(4) ![]()
したがって、
(5) ![]()
これより以下を得る。
(6) 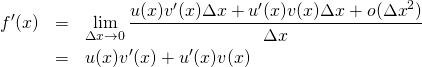
(8) ![]()
(9) ![]()
これより(7)を得る。
(10) 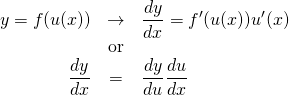
![]() とおくと、
とおくと、
(11) 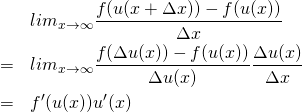
(12) 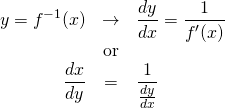
(13) ![]()
とおいて、合成関数の微分より、
(14) 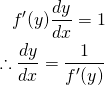
(15) 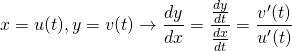
![]() 、
、![]() とおいて、
とおいて、
(16) ![]()
定数数列の和は、定数の項数倍。
(1) 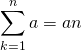
等差数列![]() の和は、初項と末項の和に項数を乗じた数の1/2。
の和は、初項と末項の和に項数を乗じた数の1/2。
(2) 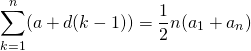
特に、
(3) 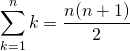
等差数列の![]() 項目までの和を
項目までの和を![]() とすると、
とすると、
(4) 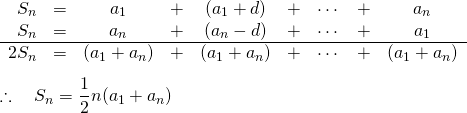
式(3)を使って、
(5) 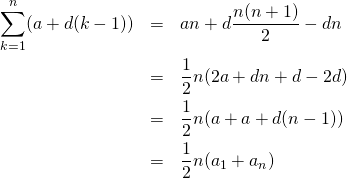
等比数列![]() の和は以下の通り。
の和は以下の通り。
(6) 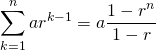
特に、
(7) 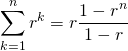
等差数列の![]() 項目までの和を
項目までの和を![]() とすると、
とすると、
(8) 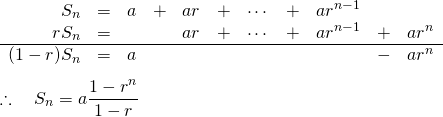
等差部分と等比部分の両方を含んだ数列の部分和。
(9) 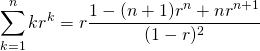
一般的な部分和の差を用いる方法。
(10) 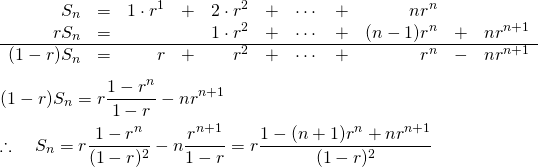
微分を用いる方法。等比数列の公式、
(11) 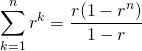
の両辺を![]() で微分すると、
で微分すると、
(12) 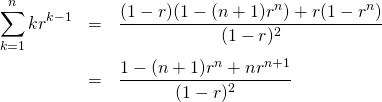
両辺を![]() 倍して同じ式を得る。
倍して同じ式を得る。
(13) 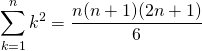
以下の式から出発する。
(14) 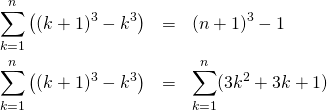
これより、
(15) 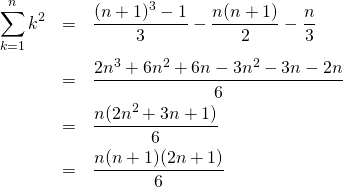
(16) 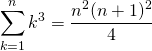
上記と同じように、
(17) 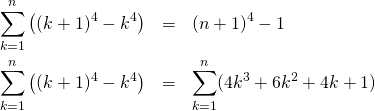
これより、
(18) 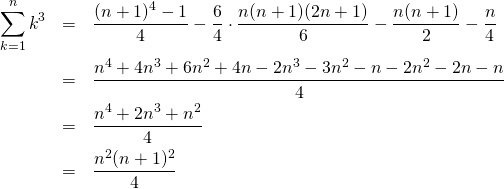
数列![]() の階差数列が扱いやすい数列の場合。
の階差数列が扱いやすい数列の場合。
(19) ![]()
![]() の各項は、
の各項は、![]() ~
~![]() の和をとることで以下のように得られる。
の和をとることで以下のように得られる。
(20) 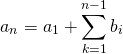
【例】
![]() の階差数列が
の階差数列が![]() で
で![]() のときの数列
のときの数列![]() は以下のようになる
は以下のようになる
![]()
この数列の一般項は、
(21) 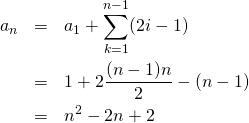
上式は![]() の時も初期条件
の時も初期条件![]() を満足する。
を満足する。