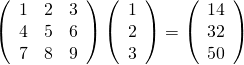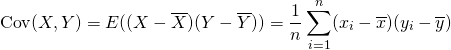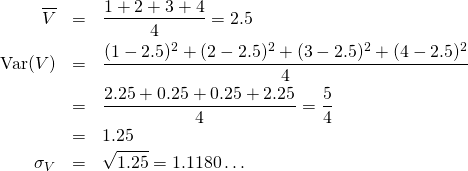Python3 – KMeansClustering

2019-11-10 / tau / 3件のコメント

概要

k平均法(k-means clustering)はクラスタリングの手法の1つで、与えられたデータ群の特徴と初期値に基づいて、データを並列(非階層)のクラスターに分類する。

アルゴリズムはシンプルで、以下の手順。

クラスターの数だけクラスターの代表点の初期値を設定する
代表点の位置が収束するまで以下を繰り返す
1. データの各点から最も近い代表点を選ぶ
2. 同じ代表点の点群から重心を算出し、新しい代表点の位置とする

このクラスは、特徴量が2つのデータ群と代表点の初期値を与えて、k平均法でクラスタリングを行うテストクラス。

2つの特徴量x_data、y_dataを与えてオブジェクトを生成し、代表点の初期値x_means、y_meansを与えてメソッドを実行して結果を得る。

全コード

KMeansClusteringクラスの全コードは以下の通り。

import numpy as np
import sys


class KMeansClustering:
    def __init__(self, x_data, y_data):
        self._x = x_data
        self._y = y_data
        self._x_means = None
        self._y_means = None
        self._num_data = len(self._x)
        self._num_means = 0
        self._groups = np.empty((0, self._num_data), dtype=int)

    def _distance(self, x0, y0, x1, y1):
        return (x0 - x1)**2 + (y0 - y1)**2

    def _point_converged(self, x0, y0, x1, y1):
        return True if x0==x1 and y0==y1 else False

    def _all_points_converged(self, x_old, y_old, x_new, y_new):
        for x0, y0, x1, y1 in zip(x_old, y_old, x_new, y_new):
            if not self._point_converged(x0, y0, x1, y1):
                return False
        return True

    def _set_nearest_mean_point(self):
        groups = np.zeros(self._num_data, int)
        for i, (x, y) in enumerate(zip(self._x, self._y)):
            min_dist = sys.float_info.max
            for j, (xm, ym) in \
                    enumerate(zip(self._x_means[-1], self._y_means[-1])):
                d = self._distance(x, y, xm, ym)
                if d < min_dist:
                    groups[i] = j
                    min_dist = d
        self._groups = np.vstack((self._groups, groups))

    def _revise_mean_points(self):
        x_means_new = np.zeros(self._num_means)
        y_means_new = np.zeros(self._num_means)

        for k in range(self._num_means):
            target = [True if j==k else False for j in self._groups[-1]]
            x_means_new[k] = np.mean(self._x[target])
            y_means_new[k] = np.mean(self._y[target])

        return x_means_new, y_means_new

    def get_result(self, x_means, y_means):
        self._x_means = np.array([x_means.copy()])
        self._y_means = np.array([y_means.copy()])
        self._num_means = len(x_means)

        while True:
            self._set_nearest_mean_point()
            xm, ym = self._revise_mean_points()

            if self._all_points_converged( \
                    self._x_means[-1], self._y_means[-1], xm, ym):
                return self._x_means, self._y_means, self._groups
            else:
                self._x_means = np.vstack((self._x_means, xm))
                self._y_means = np.vstack((self._y_means, ym))

        return self._x_means, self._y_means, self._groups

import numpy as np

import sys

class KMeansClustering:

def __init__(self, x_data, y_data):

self._x = x_data

self._y = y_data

self._x_means = None

self._y_means = None

self._num_data = len(self._x)

self._num_means = 0

self._groups = np.empty((0, self._num_data), dtype=int)

def _distance(self, x0, y0, x1, y1):

return (x0 - x1)**2 + (y0 - y1)**2

def _point_converged(self, x0, y0, x1, y1):

return True if x0==x1 and y0==y1 else False

def _all_points_converged(self, x_old, y_old, x_new, y_new):

for x0, y0, x1, y1 in zip(x_old, y_old, x_new, y_new):

if not self._point_converged(x0, y0, x1, y1):

return False

return True

def _set_nearest_mean_point(self):

groups = np.zeros(self._num_data, int)

for i, (x, y) in enumerate(zip(self._x, self._y)):

min_dist = sys.float_info.max

for j, (xm, ym) in \

enumerate(zip(self._x_means[-1], self._y_means[-1])):

d = self._distance(x, y, xm, ym)

if d < min_dist:

groups[i] = j

min_dist = d

self._groups = np.vstack((self._groups, groups))

def _revise_mean_points(self):

x_means_new = np.zeros(self._num_means)

y_means_new = np.zeros(self._num_means)

for k in range(self._num_means):

target = [True if j==k else False for j in self._groups[-1]]

x_means_new[k] = np.mean(self._x[target])

y_means_new[k] = np.mean(self._y[target])

return x_means_new, y_means_new

def get_result(self, x_means, y_means):

self._x_means = np.array([x_means.copy()])

self._y_means = np.array([y_means.copy()])

self._num_means = len(x_means)

while True:

self._set_nearest_mean_point()

xm, ym = self._revise_mean_points()

if self._all_points_converged( \

self._x_means[-1], self._y_means[-1], xm, ym):

return self._x_means, self._y_means, self._groups

else:

self._x_means = np.vstack((self._x_means, xm))

self._y_means = np.vstack((self._y_means, ym))

return self._x_means, self._y_means, self._groups

利用方法

クラスタリングを行うインスタンスの生成

初期データを与え、KMeansClusteringクラスのインスタンスを生成する。

clustering = KMeansClustering(x_data, y_data)

1	clustering = KMeansClustering(x_data, y_data)

コンストラクターに与える引数は以下の通り。

x_data, y_data: クラスタリングを行うデータの特徴量x、yの配列(1次元のndarray)。

クラスタリングの実行

生成したインスタンスに対して、クラスタリングを行うメソッドを実行して結果を得る。

xm, ym, groups = clustering.get_result(x_means, y_means)

1	xm, ym, groups = clustering.get_result(x_means, y_means)

メソッドに与える引数は以下の通り。

x_means, y_means: k個のクラスターの代表点の初期値(1次元のndarray)。

結果は以下のタプルで与えられる。

x_means, y_means: クラスターの代表点のx、yの配列。収束までの各計算段階の値を記録しており、2次元のndarrayの各行が各計算ステップに相当。
groups: 各データが属するクラスター(代表点)番号のndarray。

実行例

以下のコードでKMeansClusteringクラスをテスト。内容は以下の通り。

2つの円状に散らばるランダムな点群を発生させ、1つのデータとしてまとめる
- random_scatter_dataは指定した中心・半径の円内に指定した数のランダムな点を発生させるモジュールで、別途作成（最後の方にコードを掲載）
クラスターの代表点の数と位置、散布図を描画するパラメーターを設定する
- プロットする図の数は2行3列で固定し、初期状態を除いた5つの図を表示させる
- 予め実行させてコンソールで収束回数を確認し、33行目で表示させる計算ステップを指定している
初期状態の散布図をプロット
クラスタリングを行うKMeansClustringオブジェクトを生成し、結果を得るためのメソッドを実行(53-54行目)
結果をプロット

import numpy as np
import matplotlib.pyplot as plt
import random_scatter_data as rsd
from k_means_clustering import KMeansClustering


##################################################
# generate random points
#
np.random.seed(10)

num_data_1 = 100
num_data_2 = 100

x1, y1 = rsd.scatter_in_circle(15, 15, 10, num=num_data_1)
x2, y2 = rsd.scatter_in_circle(25, 25, 10, num=num_data_2)

x_data = np.hstack((x1, x2))
y_data = np.hstack((y1, y2))

##################################################
# settings
#
k = 2
x_means = np.zeros(k)
y_means = np.zeros(k)
x_means[0], y_means[0] = 15, 15
x_means[1], y_means[1] = 20, 15

x_lim = 40
y_lim = 40

plot_steps = [0, 1, 2, 4, 6]
plot_rows = 2
plot_cols = 3

##################################################
# plot initial state with original cluster
#
fig = plt.figure(figsize=(8, 6))

ax = fig.add_subplot(plot_rows, plot_cols, 1, aspect=1.0)
ax.set_xlim(0, x_lim)
ax.set_ylim(0, y_lim)

ax.scatter(x1, y1, s=5)
ax.scatter(x2, y2, s=5)
ax.scatter(x_means, y_means, c='red', marker='x')

##################################################
# create clustring object and get result
#
clustering = KMeansClustering(x_data, y_data)
xm, ym, groups = clustering.get_result(x_means, y_means)

print("convergion times = {}".format(len(xm)))
for n_mean in range(k):
    print("[{}, {}]".format(xm[-1][n_mean], ym[-1][n_mean]))

##################################################
# plot the states of designated steps
#
for n_plot, n_step in enumerate(plot_steps):
    ax = fig.add_subplot(plot_rows, plot_cols, n_plot + 2, aspect=1.0)
    ax.set_xlim(0, x_lim)
    ax.set_ylim(0, y_lim)
    for j in range(k):
        target = [True if jj==j else False for jj in groups[n_step]]
        ax.scatter(x_data[target], y_data[target], s=5)
        ax.scatter(xm[n_step], ym[n_step], marker='x')

plt.show()

import numpy as np

import matplotlib.pyplot as plt

import random_scatter_data as rsd

from k_means_clustering import KMeansClustering

##################################################

# generate random points

np.random.seed(10)

num_data_1 = 100

num_data_2 = 100

x1, y1 = rsd.scatter_in_circle(15, 15, 10, num=num_data_1)

x2, y2 = rsd.scatter_in_circle(25, 25, 10, num=num_data_2)

x_data = np.hstack((x1, x2))

y_data = np.hstack((y1, y2))

##################################################

# settings

k = 2

x_means = np.zeros(k)

y_means = np.zeros(k)

x_means[0], y_means[0] = 15, 15

x_means[1], y_means[1] = 20, 15

x_lim = 40

y_lim = 40

plot_steps = [0, 1, 2, 4, 6]

plot_rows = 2

plot_cols = 3

##################################################

# plot initial state with original cluster

fig = plt.figure(figsize=(8, 6))

ax = fig.add_subplot(plot_rows, plot_cols, 1, aspect=1.0)

ax.set_xlim(0, x_lim)

ax.set_ylim(0, y_lim)

ax.scatter(x1, y1, s=5)

ax.scatter(x2, y2, s=5)

ax.scatter(x_means, y_means, c='red', marker='x')

##################################################

# create clustring object and get result

clustering = KMeansClustering(x_data, y_data)

xm, ym, groups = clustering.get_result(x_means, y_means)

print("convergion times = {}".format(len(xm)))

for n_mean in range(k):

print("[{}, {}]".format(xm[-1][n_mean], ym[-1][n_mean]))

##################################################

# plot the states of designated steps

for n_plot, n_step in enumerate(plot_steps):

ax = fig.add_subplot(plot_rows, plot_cols, n_plot + 2, aspect=1.0)

ax.set_xlim(0, x_lim)

ax.set_ylim(0, y_lim)

for j in range(k):

target = [True if jj==j else False for jj in groups[n_step]]

ax.scatter(x_data[target], y_data[target], s=5)

ax.scatter(xm[n_step], ym[n_step], marker='x')

plt.show()

このコードの実行結果はコンソールで以下のように表示される。

convergion times = 7
[14.567003574164632, 15.215775486294216]
[25.31190419286806, 25.871321239241027]
[Finished in 3.529s]

convergion times = 7

[14.567003574164632, 15.215775486294216]

[25.31190419286806, 25.871321239241027]

[Finished in 3.529s]

この結果から1、2、3、5、7回目の計算結果を図示するよう上のコードでセットした表示結果は以下の通り。

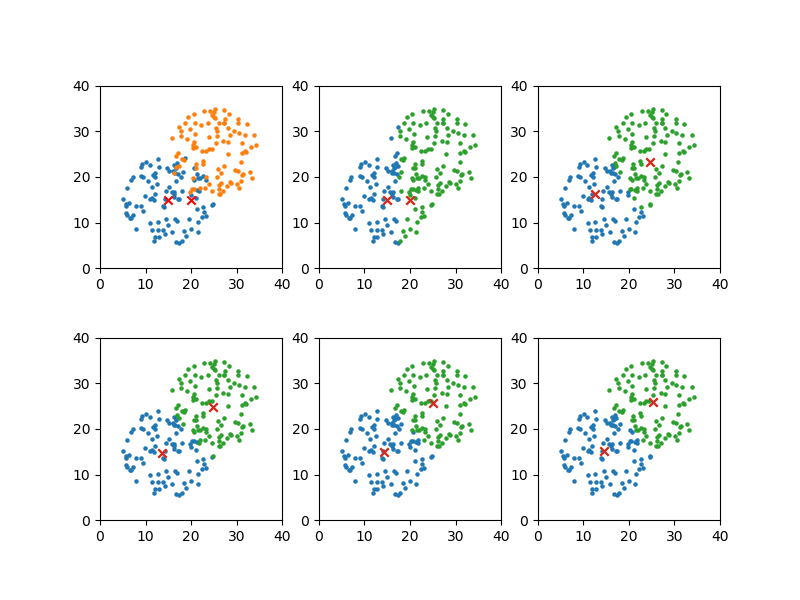
グループが比較的明確なので、早い段階で代表点の位置が定まっている。

クラス説明

`init()`～インスタンス生成

    def __init__(self, x_data, y_data):
        self._x = x_data
        self._y = y_data
        self._x_means = None
        self._y_means = None
        self._num_data = len(self._x)
        self._num_means = 0
        self._groups = np.empty((0, self._num_data), dtype=int)

def __init__(self, x_data, y_data):

self._x = x_data

self._y = y_data

self._x_means = None

self._y_means = None

self._num_data = len(self._x)

self._num_means = 0

self._groups = np.empty((0, self._num_data), dtype=int)

クラスタリングを行うデータの特徴量x_data、y_dataをndarrayで与えてインスタンスを生成。

プライベート・メンバーは以下の通り。

_x, _y: クラスタリングを行うデータの2つの特徴量の配列。計算過程で変更されない。
_x_means, _y_means: 代表点の計算結果を保存していく配列。分析実行時に初期値が与えられるため、初期値はNone。
_num_data: データの個数。
_num_means: 代表点(クラスターの個数)。代表点が分析実行時に与えられるため、初期値は0。
_groups: 各データの属するクラスターを保存していく配列。

`get_result()`～分析の実行

    def get_result(self, x_means, y_means):
        self._x_means = np.array([x_means.copy()])
        self._y_means = np.array([y_means.copy()])
        self._num_means = len(x_means)

        while True:
            self._set_nearest_mean_point()
            xm, ym = self._revise_mean_points()

            if self._all_points_converged( \
                    self._x_means[-1], self._y_means[-1], xm, ym):
                return self._x_means, self._y_means, self._groups
            else:
                self._x_means = np.vstack((self._x_means, xm))
                self._y_means = np.vstack((self._y_means, ym))

        return self._x_means, self._y_means, self._groups

def get_result(self, x_means, y_means):

self._x_means = np.array([x_means.copy()])

self._y_means = np.array([y_means.copy()])

self._num_means = len(x_means)

while True:

self._set_nearest_mean_point()

xm, ym = self._revise_mean_points()

if self._all_points_converged( \

self._x_means[-1], self._y_means[-1], xm, ym):

return self._x_means, self._y_means, self._groups

else:

self._x_means = np.vstack((self._x_means, xm))

self._y_means = np.vstack((self._y_means, ym))

return self._x_means, self._y_means, self._groups

k個の代表点のx、yを引数として渡し、結果を得る。

引数

_x_means, _y_means: k個の代表点の初期値x、yを、それぞれ1次元のndarrayで与える。引数で与えた配列は変更されない。

戻り値

x_means, y_means: 代表点の計算結果が保存された配列。各行は計算ステップに相当。

groups: 各計算ステップにおける、各点のクラスターが保存された配列。各行は計算ステップに相当。

処理内容

代表点の初期値をプライベート・メンバーにコピーし、代表点の個数をセット
全ての代表点の位置が収束するまで、以下を繰り返す
1. 各データについて、最も近い代表点をセット
2. 共通の代表点を持つデータから、新しい代表点の位置を計算
3. 代表点の前回最後の計算値と今回の計算値が収束したならループ終了、でなければ計算結果を追加してループ継続
計算結果を戻り値として終了

プライベートメソッド

`_distance()`～2点間の距離

    def _distance(self, x0, y0, x1, y1):
        return (x0 - x1)**2 + (y0 - y1)**2

1 2	def _distance(self, x0, y0, x1, y1): return (x0 - x1)2 + (y0 - y1)2

2つの点の距離を与える。ここではユークリッド距離の2乗。

`_point_converged()`～収束判定

    def _point_converged(self, x0, y0, x1, y1):
        return True if x0==x1 and y0==y1 else False

1 2	def _point_converged(self, x0, y0, x1, y1): return True if x0==x1 and y0==y1 else False

2つの点の座標から、点の位置が収束したかどうかを判定。

本来、各座標値はfloatなので'=='による判定は危険だが、ここでは収束の速さと確実性を信じて簡易に設定。

`_all_points_converged()`～全ての点の収束判定

    def _all_points_converged(self, x_old, y_old, x_new, y_new):
        for x0, y0, x1, y1 in zip(x_old, y_old, x_new, y_new):
            if not self._point_converged(x0, y0, x1, y1):
                return False
        return True

def _all_points_converged(self, x_old, y_old, x_new, y_new):

for x0, y0, x1, y1 in zip(x_old, y_old, x_new, y_new):

if not self._point_converged(x0, y0, x1, y1):

return False

return True

配列で与えた2組の点がすべて収束条件を満たしているか判定。

`_set_nearest_mean_point()`～各点に最も近い代表点

    def _set_nearest_mean_point(self):
        groups = np.zeros(self._num_data, int)
        for i, (x, y) in enumerate(zip(self._x, self._y)):
            min_dist = sys.float_info.max
            for j, (xm, ym) in \
                    enumerate(zip(self._x_means[-1], self._y_means[-1])):
                d = self._distance(x, y, xm, ym)
                if d < min_dist:
                    groups[i] = j
                    min_dist = d
        self._groups = np.vstack((self._groups, groups))

def _set_nearest_mean_point(self):

groups = np.zeros(self._num_data, int)

for i, (x, y) in enumerate(zip(self._x, self._y)):

min_dist = sys.float_info.max

for j, (xm, ym) in \

enumerate(zip(self._x_means[-1], self._y_means[-1])):

d = self._distance(x, y, xm, ym)

if d < min_dist:

groups[i] = j

min_dist = d

self._groups = np.vstack((self._groups, groups))

処理内容

各データについて、それぞれから最も近い距離にある代表点を探し、その番号を1次元の配列groupsに記録
_groups配列に、今回の分類結果を行として追加

`_revise_mean_points()`～代表点の更新

    def _revise_mean_points(self):
        x_means_new = np.zeros(self._num_means)
        y_means_new = np.zeros(self._num_means)

        for k in range(self._num_means):
            target = [True if j==k else False for j in self._groups[-1]]
            x_means_new[k] = np.mean(self._x[target])
            y_means_new[k] = np.mean(self._y[target])

        return x_means_new, y_means_new

def _revise_mean_points(self):

x_means_new = np.zeros(self._num_means)

y_means_new = np.zeros(self._num_means)

for k in range(self._num_means):

target = [True if j==k else False for j in self._groups[-1]]

x_means_new[k] = np.mean(self._x[target])

y_means_new[k] = np.mean(self._y[target])

return x_means_new, y_means_new

同じ代表点に属するデータからそれらの重心を計算し、新しい代表点として返す。

random_scatter_data.py

今回整理のためにつくったモジュールで、内容は以下の通り。

import numpy as np


def scatter_in_circle(x_org=0, y_org=0, r=1, num=100):
    x = np.zeros(num)
    y = np.zeros(num)

    for i in range(num):
        while True:
            xw = np.random.rand() * 2 * r - r
            yw = np.random.rand() * 2 * r - r
            if xw*xw + yw*yw <= r*r:
                x[i], y[i] = xw + x_org, yw + y_org
                break
    return x, y


def scatter_in_2dnormal(x_org=0, y_org=0, r=1, nsigma=1, num=100):
    x = np.random.randn(num) * r/nsigma + x_org
    y = np.random.randn(num) * r/nsigma + y_org
    return x, y

import numpy as np

def scatter_in_circle(x_org=0, y_org=0, r=1, num=100):

x = np.zeros(num)

y = np.zeros(num)

for i in range(num):

while True:

xw = np.random.rand() * 2 * r - r

yw = np.random.rand() * 2 * r - r

if xw*xw + yw*yw <= r*r:

x[i], y[i] = xw + x_org, yw + y_org

break

return x, y

def scatter_in_2dnormal(x_org=0, y_org=0, r=1, nsigma=1, num=100):

x = np.random.randn(num) * r/nsigma + x_org

y = np.random.randn(num) * r/nsigma + y_org

return x, y

Python3 – 2次元配列への行・列の追加

2019-11-10 / tau / コメントする

概要

2次元配列をデータテーブルのように使っていて、行や列を追加する場合の方法を整理。

リストの場合とndarrayの場合それぞれについて、行の追加、列の追加のためのメソッドや関数と、その使い方の注意を記しておく。

結論として、ndarrayを使う場合はnumpy.vstack()関数、numpy.hstack()関数を用いるのが、配列の2次元化や追加方向のaxis指定がなく紛れがない。

リストの場合

リストの場合はappend()メソッド、insert()メソッドで行や列を追加する。ただし、より現実的な方法をこちらに整理した。

注意点

リストのappend()メソッド、insert()メソッドは元のリストを書き換える
各メソッドは戻り値を持たない(None)
初期データが1行／1列の場合に2次元配列であることを明示する必要がある

初期リストが空の場合は単に1次元の空のリストを準備すればいいので、初期リストがある場合でも、空のリストを準備してからそこに追加するように決めておけばミスは減りそう。

行の追加

`append()`メソッド

append()メソッドは素直に引数のリストをもとのリストに追加する。ただし、下のコードの1行目のように元のリストが2次元配列であることを明示しなければならない。

a = [[0, 1, 2]]
print(a)
b = [3, 4, 5]
a.append(b)
print(a)

# [[0, 1, 2]]
# [[0, 1, 2], [3, 4, 5]]

a = [[0, 1, 2]]

print(a)

b = [3, 4, 5]

a.append(b)

print(a)

# [[0, 1, 2]]

# [[0, 1, 2], [3, 4, 5]]

以下は失敗。元のリストを単なる要素リストで定義してしまうと、追加するリストが要素の一つとして扱われてしまう。

a = [0, 1, 2]
print(a)
b = [3, 4, 5]
a.append(b)
print(a)

# [0, 1, 2]
# [0, 1, 2, [3, 4, 5]]

a = [0, 1, 2]

print(a)

b = [3, 4, 5]

a.append(b)

print(a)

# [0, 1, 2]

# [0, 1, 2, [3, 4, 5]]

空のリストへの追加。

この場合は1次元の空のリストを用意すれば、追加されるリストが要素として順次追加されていく。

a = []
print(a)
b = [0, 1, 2]
a.append(b)
print(a)
b = [3, 4, 5]
a.append(b)
print(a)

# []
# [[0, 1, 2]]
# [[0, 1, 2], [3, 4, 5]]

a = []

print(a)

b = [0, 1, 2]

a.append(b)

print(a)

b = [3, 4, 5]

a.append(b)

print(a)

# []

# [[0, 1, 2]]

# [[0, 1, 2], [3, 4, 5]]

`insert()`メソッド

insert()メソッドも素直にリストを追加してくれるが、追加位置を指定するのに一手間かかる。行の最後に追加するときは、追加位置をlen(元のリスト)で指定する

その他の仕様はappend()メソッドと同じ。

a = [[0, 1, 2]]
print(a)
b = [3, 4, 5]
a.insert(len(a), b)
print(a)

# [[0, 1, 2]]
# [[0, 1, 2], [3, 4, 5]]

a = [[0, 1, 2]]

print(a)

b = [3, 4, 5]

a.insert(len(a), b)

print(a)

# [[0, 1, 2]]

# [[0, 1, 2], [3, 4, 5]]

空のリストへの追加もappend()メソッドと同様。

a = []
print(a)
b = [0, 1, 2]
a.insert(len(a), b)
print(a)
b = [3, 4, 5]
a.insert(len(a), b)
print(a)

# []
# [[0, 1, 2]]
# [[0, 1, 2], [3, 4, 5]]

a = []

print(a)

b = [0, 1, 2]

a.insert(len(a), b)

print(a)

b = [3, 4, 5]

a.insert(len(a), b)

print(a)

# []

# [[0, 1, 2]]

# [[0, 1, 2], [3, 4, 5]]

列の追加

列の追加の場合、各要素が縦に並んだ列ベクトルとしての定義になる。

`append()`メソッド

行の追加と同様。最初の1列から定義する場合、明示的に列ベクトルの2次元配列であることを明示する必要がある。

a = [[[0], [1], [2]]]
print(a)
b = [[3], [4], [5]]
a.append(b)
print(a)

# [[[0], [1], [2]]]
# [[[0], [1], [2]], [[3], [4], [5]]]

a = [[[0], [1], [2]]]

print(a)

b = [[3], [4], [5]]

a.append(b)

print(a)

# [[[0], [1], [2]]]

# [[[0], [1], [2]], [[3], [4], [5]]]

空のリストへの追加の場合は、行の追加と同様シンプル。

a = []
print(a)
b = [[0], [1], [2]]
a.append(b)
print(a)
b = [[3], [4], [5]]
a.append(b)
print(a)

# []
# [[[0], [1], [2]]]
# [[[0], [1], [2]], [[3], [4], [5]]]

a = []

print(a)

b = [[0], [1], [2]]

a.append(b)

print(a)

b = [[3], [4], [5]]

a.append(b)

print(a)

# []

# [[[0], [1], [2]]]

# [[[0], [1], [2]], [[3], [4], [5]]]

`insert()`メソッド

insert()メソッドの場合も行の追加と同様。

a = [[[0], [1], [2]]]
print(a)
b = [[3], [4], [5]]
a.insert(len(a), b)
print(a)

# [[[0], [1], [2]]]
# [[[0], [1], [2]], [[3], [4], [5]]]

a = [[[0], [1], [2]]]

print(a)

b = [[3], [4], [5]]

a.insert(len(a), b)

print(a)

# [[[0], [1], [2]]]

# [[[0], [1], [2]], [[3], [4], [5]]]

空のリストへの追加も行の追加と同様。

a = []
print(a)
b = [[0], [1], [2]]
a.insert(len(a), b)
print(a)
b = [[3], [4], [5]]
a.insert(len(a), b)
print(a)

# []
# [[[0], [1], [2]]]
# [[[0], [1], [2]], [[3], [4], [5]]]

a = []

print(a)

b = [[0], [1], [2]]

a.insert(len(a), b)

print(a)

b = [[3], [4], [5]]

a.insert(len(a), b)

print(a)

# []

# [[[0], [1], [2]]]

# [[[0], [1], [2]], [[3], [4], [5]]]

`ndarray`の場合

ndarrayの場合は、numpyのモジュール関数append()、insert()のほか、hstack()関数、vstack()関数も使える。

注意点

リストのメソッドと異なり、numpyの各モジュール関数は元の配列を変更せず、変更後の新たな配列を戻り値として返す
append()関数、insert()関数では、行の追加／列の追加に応じて引数axisを指定する
append()関数は、行を追加する場合は追加する配列も2次元で明示する必要があるが、列を追加する場合にはそのまま指定する
空の配列はempty()関数で準備し、型を指定しておく
hstack()関数、vstack()関数は、元の配列と追加する配列をタプルで指定する

行の追加

ndarrayで行を追加する場合、numpyモジュールのappend()関数、insert()関数でaxis=0を指定するか、vstack()関数を利用する。

`numpy.append()`関数

初期配列が2次元であることを明示しなければならない点はリストのappend()メソッドと同じだが、追加配列でもこれが必要になる。

numpy.append(元の配列, 追加する配列, axis=0)

追加する配列は、元の配列と次元・列数があっていなければならない
→行ベクトルでもndarrayの2次元配列としなければならない
→下記コード例では4行目のnp.array([b])
→こうしないと”次元が合わない”としてエラーになる
追加する配列を行として追加する場合は、axis=0の指定が必須(これを指定しないと、単に元の要素に続いて追加配列の要素が追加されるだけ)

a = np.array([[0, 1, 2]])
print(a)
b = np.array([3, 4, 5])
print(np.append(a, np.array([b]), axis=0))

# [[0 1 2]]
# [[0 1 2]
#  [3 4 5]]

a = np.array([[0, 1, 2]])

print(a)

b = np.array([3, 4, 5])

print(np.append(a, np.array([b]), axis=0))

# [[0 1 2]]

# [[0 1 2]

# [3 4 5]]

空の配列への追加の場合、numpy.empty(0, n)で空の配列を準備する。

numpy.empty((行数, 列数), dtype=型)

確保する配列の各次元のサイズはタプルで指定
行が空なので行数は0で指定
dtype引数で型を明示しないとデフォルトのfloat型になる

a = np.empty((0, 3), dtype=int)
print(a)
b = np.array([0, 1, 2])
a = np.append(a, np.array([b]), axis=0)
print(a)
b = np.array([3, 4, 5])
a = np.append(a, np.array([b]), axis=0)
print(a)

# []
# [[0 1 2]]
# [[0 1 2]
#  [3 4 5]]

a = np.empty((0, 3), dtype=int)

print(a)

b = np.array([0, 1, 2])

a = np.append(a, np.array([b]), axis=0)

print(a)

b = np.array([3, 4, 5])

a = np.append(a, np.array([b]), axis=0)

print(a)

# []

# [[0 1 2]]

# [[0 1 2]

# [3 4 5]]

`numpy.insert()`関数

リストのinsert()メソッドと同様だが、いくつか注意が必要。

numpy.insert(元の配列, 追加する行位置, 追加する配列, axis=0)

追加する位置は最後の行の次の行番号で、これは元の配列のshapeプロパティーで得られる(shape[0]は配列各次元のサイズで、2次元配列の場合shape[0]は行数、shape[1]は列数を表す)
追加する配列はそのまま指定する(2次元で定義しない)
→追加する配列は2次元化しても同じ結果になる
axis=0の指定が必要

a = np.array([np.array([0, 1, 2])])
print(a)
b = np.array([3, 4, 5])
print(np.insert(a, a.shape[0], b, axis=0))

# [[0 1 2]]
# [[0 1 2]
#  [3 4 5]]

a = np.array([np.array([0, 1, 2])])

print(a)

b = np.array([3, 4, 5])

print(np.insert(a, a.shape[0], b, axis=0))

# [[0 1 2]]

# [[0 1 2]

# [3 4 5]]

空の配列への追加する場合は、元の配列をnumpy.empty(0, n)で生成。

a = np.empty((0, 3), dtype=int)
print(a)
b = np.array([0, 1, 2])
a = np.insert(a, a.shape[0], b, axis=0)
print(a)
b = np.array([3, 4, 5])
a = np.insert(a, a.shape[0], b, axis=0)
print(a)

# []
# [[0 1 2]]
# [[0 1 2]
#  [3 4 5]]

a = np.empty((0, 3), dtype=int)

print(a)

b = np.array([0, 1, 2])

a = np.insert(a, a.shape[0], b, axis=0)

print(a)

b = np.array([3, 4, 5])

a = np.insert(a, a.shape[0], b, axis=0)

print(a)

# []

# [[0 1 2]]

# [[0 1 2]

# [3 4 5]]

`numpy.vstack()`関数

numpy.vstack()関数は引数に2以上の配列を指定し、それらを縦に連結していく。特に2次元配列化や軸の指定の必要はない。

a = np.array([0, 1, 2])
print(a)
b = np.array([3, 4, 5])
print(np.vstack((a, b)))

# [0 1 2]
# [[0 1 2]
#  [3 4 5]]

a = np.array([0, 1, 2])

print(a)

b = np.array([3, 4, 5])

print(np.vstack((a, b)))

# [0 1 2]

# [[0 1 2]

# [3 4 5]]

空の配列への追加の場合は、numpy.empty(0, n)で生成した空の配列を含めて、順次タプルの中に追加したい配列を指定するだけでよい。

a = np.empty((0, 3), int)
print(a)
b = np.array([0, 1, 2])
c = np.array([3, 4, 5])
print(np.vstack((a, b, c)))

# []
# [[0 1 2]
#  [3 4 5]]

a = np.empty((0, 3), int)

print(a)

b = np.array([0, 1, 2])

c = np.array([3, 4, 5])

print(np.vstack((a, b, c)))

# []

# [[0 1 2]

# [3 4 5]]

列の追加

ndarrayを列として追加していく場合、追加する配列も列形式である必要がある。列方向の追加をaxis引数で指定する必要がある。

通常の行形式の1次元配列を列として追加する場合、reshape(列数, 1)で列ベクトル化する
追加するベクトルを[]で囲って2次元化する必要はない
axisi=1で列方向の追加として指定

`numpy.append()`関数

行の追加の時と違って、元の配列も追加する配列も2次元化しない。

a = np.array([0, 1, 2]).reshape(3, 1)
print(a)
b = np.array([3, 4, 5]).reshape(3, 1)
print(np.append(a, b, axis=1))

# [[0]
#  [1]
#  [2]]
# [[0 3]
#  [1 4]
#  [2 5]]

a = np.array([0, 1, 2]).reshape(3, 1)

print(a)

b = np.array([3, 4, 5]).reshape(3, 1)

print(np.append(a, b, axis=1))

# [[0]

# [1]

# [2]]

# [[0 3]

# [1 4]

# [2 5]]

空の配列への追加は、列数をゼロとしてnumpy.empty(n, 0)で指定する。

a = np.empty((3, 0), dtype=int)
print(a)
b = np.array([0, 1, 2]).reshape(3, 1)
a = np.append(a, b, axis=1)
print(a)
b = np.array([3, 4, 5]).reshape(3, 1)
a = np.append(a, b, axis=1)
print(a)

# []
# [[0]
#  [1]
#  [2]]
# [[0 3]
#  [1 4]
#  [2 5]]

a = np.empty((3, 0), dtype=int)

print(a)

b = np.array([0, 1, 2]).reshape(3, 1)

a = np.append(a, b, axis=1)

print(a)

b = np.array([3, 4, 5]).reshape(3, 1)

a = np.append(a, b, axis=1)

print(a)

# []

# [[0]

# [1]

# [2]]

# [[0 3]

# [1 4]

# [2 5]]

`numpy.insert()`関数

numpy.insert()関数も行の追加と同じだが、以下の点に注意。

列の追加位置(最後の列の次)は元の変数のshapeプロパティーの2つ目shape[1]で指定する
追加する配列は2次元化せずそのまま指定
列方向の追加なのでaxis=1を指定する

a = np.array([0, 1, 2]).reshape(3, 1)
print(a)
b = np.array([3, 4, 5])
print(np.insert(a, a.shape[1], b, axis=1))

# [[0]
#  [1]
#  [2]]
# [[0 3]
#  [1 4]
#  [2 5]]

a = np.array([0, 1, 2]).reshape(3, 1)

print(a)

b = np.array([3, 4, 5])

print(np.insert(a, a.shape[1], b, axis=1))

# [[0]

# [1]

# [2]]

# [[0 3]

# [1 4]

# [2 5]]

空の配列への追加はこれまでと同様。

a = np.empty((3, 0), dtype=int)
print(a)
b = np.array([0, 1, 2])
a = np.insert(a, a.shape[1], b, axis=1)
print(a)
b = np.array([3, 4, 5])
a = np.insert(a, a.shape[1], b, axis=1)
print(a)

# []
# [[0]
#  [1]
#  [2]]
# [[0 3]
#  [1 4]
#  [2 5]]

a = np.empty((3, 0), dtype=int)

print(a)

b = np.array([0, 1, 2])

a = np.insert(a, a.shape[1], b, axis=1)

print(a)

b = np.array([3, 4, 5])

a = np.insert(a, a.shape[1], b, axis=1)

print(a)

# []

# [[0]

# [1]

# [2]]

# [[0 3]

# [1 4]

# [2 5]]

`numpy.hstack()`関数

numpy.hstack()関数はvstack()と同様、引数に2以上の配列を指定し、それらを横に連結していく。1次元配列はreshape(-1, 1)などで列ベクトル化する必要がある。

a = np.array([0, 1, 2]).reshape(3, 1)
print(a)
b = np.array([3, 4, 5]).reshape(3, 1)
print(np.hstack((a, b)))
# [[0]
#  [1]
#  [2]]
# [[0 3]
#  [1 4]
#  [2 5]]

a = np.array([0, 1, 2]).reshape(3, 1)

print(a)

b = np.array([3, 4, 5]).reshape(3, 1)

print(np.hstack((a, b)))

# [[0]

# [1]

# [2]]

# [[0 3]

# [1 4]

# [2 5]]

空の配列への追加の場合は、numpy.empty(n, 0)で生成した空の配列から始めて、順次タプルの中に追加したい配列を指定するだけでよい。

a = np.empty((3, 0), int)
print(a)
b = np.array([0, 1, 2]).reshape(3, 1)
c = np.array([3, 4, 5]).reshape(3, 1)
print(np.hstack((a, b, c)))

# []
# [[0 3]
#  [1 4]
#  [2 5]]

a = np.empty((3, 0), int)

print(a)

b = np.array([0, 1, 2]).reshape(3, 1)

c = np.array([3, 4, 5]).reshape(3, 1)

print(np.hstack((a, b, c)))

# []

# [[0 3]

# [1 4]

# [2 5]]

Python3 – 2次元配列からの要素の取り出し

2019-11-07 / tau / 2件のコメント

概要

リスト、ndarrayの2次元配列について、いろいろな要素の取り出し方を整理する。

リストについては、以下の配列を準備する。

a = [[0, 1, 2, 3],
     [10, 11, 12, 13],
     [20, 21, 22, 23],
     [30, 31, 32, 33]]

print(a)

# [[0, 1, 2, 3], [10, 11, 12, 13], [20, 21, 22, 23], [30, 31, 32, 33]]

a = [[0, 1, 2, 3],

[10, 11, 12, 13],

[20, 21, 22, 23],

[30, 31, 32, 33]]

print(a)

# [[0, 1, 2, 3], [10, 11, 12, 13], [20, 21, 22, 23], [30, 31, 32, 33]]

ndarrayについては、以下の配列を準備する。

b = np.array([[0, 1, 2, 3],
              [10, 11, 12, 13],
              [20, 21, 22, 23],
              [30, 31, 32, 33]])

print(b)

# [[ 0  1  2  3]
#  [10 11 12 13]
#  [20 21 22 23]
#  [30 31 32 33]]

b = np.array([[0, 1, 2, 3],

[10, 11, 12, 13],

[20, 21, 22, 23],

[30, 31, 32, 33]])

print(b)

# [[ 0 1 2 3]

# [10 11 12 13]

# [20 21 22 23]

# [30 31 32 33]]

各要素の10の位が行を、1の位が列を表している。

特定要素の取り出し

リストの場合は[行番号][列番号]で取り出す。

print(a[1][2])

# 12

print(a[1][2])

# 12

ndarrayの場合もリストと同じ。

print(b[1][2])

# 12

print(b[1][2])

# 12

ただしndarrayにはもう一つの方法があって、[行番号, 列番号]でも指定できる。

print(b[1, 2])

# 12

print(b[1, 2])

# 12

行の取り出し

リストの場合[行番号]で該当する行を取り出せる。

print(a[1])

# [10, 11, 12, 13]

print(a[1])

# [10, 11, 12, 13]

スライスを使って複数行を取り出すこともできる。

print(a[1:3])

# [[10, 11, 12, 13], [20, 21, 22, 23]]

print(a[1:3])

# [[10, 11, 12, 13], [20, 21, 22, 23]]

ndarrayの場合もリストと同じ。

print(b[1])

# [10 11 12 13]

print(b[1])

# [10 11 12 13]

スライスの場合も同じ。

print(b[1:3])

# [[10 11 12 13]
#  [20 21 22 23]]

print(b[1:3])

# [[10 11 12 13]

# [20 21 22 23]]

ndarray用の指定の場合、列番号を省略。

print(b[1,])

# [10 11 12 13]

print(b[1,])

# [10 11 12 13]

行をスライス指定する場合。

print(b[1:3,])

# [[10 11 12 13]
#  [20 21 22 23]]

print(b[1:3,])

# [[10 11 12 13]

# [20 21 22 23]]

列の取り出し

ndarrayでの列の取り出し方は以下の通り。ただし、取り出された列は行方向の配列に変更される点に注意。

print(b[:, 1])

# [ 1 11 21 31]

print(b[:, 1])

# [ 1 11 21 31]

スライスを使って複数列を取り出せる。

print(b[:, 1:3])

# [[ 1  2]
#  [11 12]
#  [21 22]
#  [31 32]]

print(b[:, 1:3])

# [[ 1 2]

# [11 12]

# [21 22]

# [31 32]]

スライスを使うと、単一の列を列ベクトルとして取り出せる。

print(b[:, 1:2])

# [[ 1]
#  [11]
#  [21]
#  [31]]

print(b[:, 1:2])

# [[ 1]

# [11]

# [21]

# [31]]

reshape()で行ベクトルを列ベクトルに変換してもよい。

print(b[:, 1].reshape(4, 1))

# [[ 1]
#  [11]
#  [21]
#  [31]]

print(b[:, 1].reshape(4, 1))

# [[ 1]

# [11]

# [21]

# [31]]

なお、リスト、ndarrayとも、以下の指定方法では意図した列の抽出にならず、行の抽出になってしまう。

print(b[:][1])
print(b[:][1:3])

# [10 11 12 13]
# [[10 11 12 13]
#  [20 21 22 23]]

print(b[:][1])

print(b[:][1:3])

# [10 11 12 13]

# [[10 11 12 13]

# [20 21 22 23]]

内包表記による列指定

リスト、ndarrayとも、内包表記を使って列を取り出せる。ただし結果は行ベクトルとなる。

print([row[1] for row in b])
print(np.array([row[1] for row in b]))

# [1, 11, 21, 31]
# [ 1 11 21 31]

print([row[1] for row in b])

print(np.array([row[1] for row in b]))

# [1, 11, 21, 31]

# [ 1 11 21 31]

複数列の取り出しは以下の通り。

リストの場合、表現が少し違うが、[行番号][列番号]で要素が取り出せる。

print([row[1:3] for row in b])
print(np.array([row[1:3] for row in b]))

# [array([1, 2]), array([11, 12]), array([21, 22]), array([31, 32])]
# [[ 1  2]
#  [11 12]
#  [21 22]
#  [31 32]]

print([row[1:3] for row in b])

print(np.array([row[1:3] for row in b]))

# [array([1, 2]), array([11, 12]), array([21, 22]), array([31, 32])]

# [[ 1 2]

# [11 12]

# [21 22]

# [31 32]]

ndarray – 要素・行・列の挿入・追加

2019-11-05 / tau / コメントする

1次元配列

要素の挿入

ndarrayの1次元配列への要素の挿入にはnumpy.insert()関数を使う。第1引数に対象となる配列、第2引数に挿入位置、第3引数に挿入する値を指定。

指定された位置に値が挿入され、それ以降の要素は一つずつ後ろにずれる。

import numpy as np

a = np.array([0, 1, 2, 3])
print(np.insert(a, 2, 10))

# [ 0  1 10  2  3]

import numpy as np

a = np.array([0, 1, 2, 3])

print(np.insert(a, 2, 10))

# [ 0 1 10 2 3]

要素の追加

配列の最後に要素を追加するには、以下の方法がある。

numpy.append()
numpy.insert()
numpy.hstack()

`numpy.append()`

第1引数に配列、第2に引数に追加する要素を指定。メソッドではなく、モジュール関数。1次元配列に1次元配列を追加すると、単に要素が追加される。

print(np.append(a, 4))
print(np.append(a, np.array([4, 5, 6])))

# [0 1 2 3 4]
# [0 1 2 3 4 5 6]

print(np.append(a, 4))

print(np.append(a, np.array([4, 5, 6])))

# [0 1 2 3 4]

# [0 1 2 3 4 5 6]

`numpy.insert()`

挿入位置として最後の要素の次の位置を指定する。この値は配列のサイズと等しい。

print(np.insert(a, len(a), 20))

# [ 0  1  2  3 20]

print(np.insert(a, len(a), 20))

# [ 0 1 2 3 20]

`numpy.hstack()`

注意点として、引数として指定するのはタプルで、そのタプルの要素をつなげた結果が返される点で、追加される要素を配列としなければならない。

print(np.hstack( (a, [40]) ))

# [ 0  1  2  3 40]

print(np.hstack( (a, [40]) ))

# [ 0 1 2 3 40]

2次元配列

numpy.insert()で単純に位置指定だけすると、1次元配列として扱われてしまう。

print(np.insert(a, 2, np.array([9, 9, 9])))
print(np.insert(a, 4, np.array([9, 9, 9])))

# [0 1 9 9 9 2 3 4 5 6 7 8]
# [0 1 2 3 9 9 9 4 5 6 7 8]

print(np.insert(a, 2, np.array([9, 9, 9])))

print(np.insert(a, 4, np.array([9, 9, 9])))

# [0 1 9 9 9 2 3 4 5 6 7 8]

# [0 1 2 3 9 9 9 4 5 6 7 8]

行の挿入・追加

1次元配列を行として挿入するには、numpy.insert()で第4引数にaxis=0を指定する。

print(np.insert(a, 2, np.array([9, 9, 9]), axis=0))

# [[0 1 2]
#  [3 4 5]
#  [9 9 9]
#  [6 7 8]]

print(np.insert(a, 2, np.array([9, 9, 9]), axis=0))

# [[0 1 2]

# [3 4 5]

# [9 9 9]

# [6 7 8]]

配列の最後に行を追加するには、numpy.insert()で最終行の次の位置＝行数を指定する。

shapeプロパティーで各次元のサイズの配列が得られるので、行数として第0要素の値を使う。

print(np.insert(a, a.shape[0], np.array([9, 9, 9]), axis=0))

# [[0 1 2]
#  [3 4 5]
#  [6 7 8]
#  [9 9 9]]

print(np.insert(a, a.shape[0], np.array([9, 9, 9]), axis=0))

# [[0 1 2]

# [3 4 5]

# [6 7 8]

# [9 9 9]]

numpy.vstack()を使ってもよい。vstack()は複数の配列を縦方向につなげていく関数で、つなげる関数群を要素とするタプルを引数とする点に注意。

print(np.vstack((a, np.array([9, 9, 9]))))

# [[0 1 2]
#  [3 4 5]
#  [6 7 8]
#  [9 9 9]]

print(np.vstack((a, np.array([9, 9, 9]))))

# [[0 1 2]

# [3 4 5]

# [6 7 8]

# [9 9 9]]

列の挿入・追加

numpy.insert()で列を挿入する場合、axis=1を指定する。列の追加の場合でも、追加する配列は行形式の1次元配列で指定。

print(np.insert(a, 2, np.array([9, 9, 9]), axis=1))

# [[0 1 9 2]
#  [3 4 9 5]
#  [6 7 9 8]]

print(np.insert(a, 2, np.array([9, 9, 9]), axis=1))

# [[0 1 9 2]

# [3 4 9 5]

# [6 7 9 8]]

numpy.insert()で配列に列を追加する場合、指定位置はshapeの第1要素の値。

print(np.insert(a, a.shape[1], np.array([9, 9, 9]), axis=1))

# [[0 1 2 9]
#  [3 4 5 9]
#  [6 7 8 9]]

print(np.insert(a, a.shape[1], np.array([9, 9, 9]), axis=1))

# [[0 1 2 9]

# [3 4 5 9]

# [6 7 8 9]]

numpy.hstack()を使ってもよい。hstack()の注意点は以下の通り。

引数をタプルとすること
追加する配列は列形式とする必要があり、1次元の配列を列形式に変換すること

print(np.hstack((a, np.array([9, 9, 9]).reshape(3, 1))))

# [[0 1 2 9]
#  [3 4 5 9]
#  [6 7 8 9]]

print(np.hstack((a, np.array([9, 9, 9]).reshape(3, 1))))

# [[0 1 2 9]

# [3 4 5 9]

# [6 7 8 9]]

numpy – 連立方程式

2019-10-21 / tau / コメントする

導入

以下のように行列表示された連立方程式を考える。

$\begin{equation*} \left( \begin{array}{ccc} 1 & 2 & -3 \\ 2 & -1 & 3 \\ -3 & 2 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 5 \\ 4 \\ 1 \end{array} \right) \end{equation*}$

この方程式の解は、 $(x, y, z) = (2, 3, 1)$ 。

逆行列による方法

係数行列、未知数ベクトル、定数ベクトルをそれぞれ $\boldsymbol{A},\boldsymbol{x}, \boldsymbol{b}$ と表す。

$\begin{equation*} \boldsymbol{A} \boldsymbol{x} = \boldsymbol{b} \end{equation*}$

このとき係数行列に逆行列が存在するなら、未知数ベクトルは以下で解ける。

$\begin{gather*} \boldsymbol{A}^{-1} \boldsymbol{A} \boldsymbol{x} = \boldsymbol{A}^{-1} \boldsymbol{b} \\ \boldsymbol{x} = \boldsymbol{A}^{-1} \boldsymbol{b} \\ \end{gather*}$

これをnumpy.linalgパッケージの行列操作で解いてみる。

行列にベクトルを掛けるのに、reshape()で行ベクトルから列ベクトルに変換している点に注意。

A = np.array([[1, 2, -3],
              [2, -1, 3],
              [-3, 2, 1]])

b = np.array([5, 4, 1])
print(LA.inv(A) @ b.reshape(3, 1))

# [[2.]
#  [3.]
#  [1.]]

A = np.array([[1, 2, -3],

[2, -1, 3],

[-3, 2, 1]])

b = np.array([5, 4, 1])

print(LA.inv(A) @ b.reshape(3, 1))

# [[2.]

# [3.]

# [1.]]

numpy.linalg.solve()による方法

solve(A, b)関数は、第1引数に係数行列、第2引数に定数ベクトルを与えて、連立方程式の解のベクトルを得ることができる。

A = np.array([[1, 2, -3],
              [2, -1, 3],
              [-3, 2, 1]])

b = np.array([5, 4, 1])
print(LA.solve(A, b))

# [2. 3. 1.]

A = np.array([[1, 2, -3],

[2, -1, 3],

[-3, 2, 1]])

b = np.array([5, 4, 1])

print(LA.solve(A, b))

# [2. 3. 1.]

非正則行列の場合

以下のような、明らかな非正則行列の場合（連立方程式が不定の場合）、逆行列を計算しようとする時点でsingular matrixのエラーになる。

A = np.array([[1, 1], [2, 2]])
b = np.array([2, 4])
print(LA.inv(A))

# numpy.linalg.LinAlgError: Singular matrix

A = np.array([[1, 1], [2, 2]])

b = np.array([2, 4])

print(LA.inv(A))

# numpy.linalg.LinAlgError: Singular matrix

このようなケースでは、linalg.solve()関数でも同様のエラーとなる。

A = np.array([[1, 1], [2, 2]])
b = np.array([2, 4])
print(LA.solve(A, b))

# numpy.linalg.LinAlgError: Singular matrix

A = np.array([[1, 1], [2, 2]])

b = np.array([2, 4])

print(LA.solve(A, b))

# numpy.linalg.LinAlgError: Singular matrix

以下のようなケースはややこしい。同じ係数行列と定数ベクトルに対して、逆行列による解とsolve()による解の値が異なっている。

A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])
b = np.array([1, 2, 3])
print(LA.det(A))
print(LA.inv(A) @ b.reshape(3, 1))
print(LA.solve(A, b))

# 6.66133814775094e-16
# [[ 2.]
#  [-4.]
#  [ 0.]]
# [-0.33333333  0.66666667  0.        ]

A = np.array([[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

b = np.array([1, 2, 3])

print(LA.det(A))

print(LA.inv(A) @ b.reshape(3, 1))

print(LA.solve(A, b))

# 6.66133814775094e-16

# [[ 2.]

# [-4.]

# [ 0.]]

# [-0.33333333 0.66666667 0. ]

行列Aの行列式は理論上はゼロであることが確認できる。

$\begin{eqnarray*} \left| \begin{array}{ccc} 1 & 2 &3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right| &=& 1 \cdot (5 \cdot 9 - 6 \cdot 8) - 2 \cdot (4 \cdot 9 - 6 \cdot 7) + 3 \cdot(4 \cdot 8 - 5 \cdot 7) \\ &=& 45 - 48 -2(36 - 42) + 3(32 - 35) \\ &=& -3 +12 + 9 = 0 \end{eqnaray*}$

この方程式を掃き出し法で解いていくと以下の通り。

$\begin{equation*} \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right) \end{equation*}$

$\begin{equation*} \left( \begin{array}{ccc} 1 & 2 & 3 \\0 & -3 & -6 \\ 0 & -6 & -12 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 1 & -2 & -4 \end{array} \right) \end{equation*}$

$\begin{equation*} \left( \begin{array}{ccc} 1 & 2 & 3 \\0 & -3 & -6 \\ 0 & 0 & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} 1 & -2 & 0 \end{array} \right) \end{equation*}$

途中省略するが、ここでzを消去すると、 $y = -2x$ となり、先の計算結果と符合するが、zは0である必要はない。

不定連立方程式において、逆行列やsolve()関数を使って解く場合には注意が必要。

numpy – 行列（ndarray)

2019-10-20 / tau / コメントする

ベクトルと行列の定義

リテラル

ベクトルはnp.array()で引数にリストを指定して定義。

v = np.array([1, 2, 3])
print(v)

# [1 2 3]

v = np.array([1, 2, 3])

print(v)

# [1 2 3]

行列は同じくnp.array()で引数に二次元配列のリストを指定して定義。

m = np.array([[1, 2, 3], [4, 5, 6]])
print(m)

# [[1 2 3]
#  [4 5 6]]

m = np.array([[1, 2, 3], [4, 5, 6]])

print(m)

# [[1 2 3]

# [4 5 6]]

単位行列

numpy.identity(n)でn×nの単位行列を生成。

print(np.identity(4))

# [[1. 0. 0. 0.]
#  [0. 1. 0. 0.]
#  [0. 0. 1. 0.]
#  [0. 0. 0. 1.]]

print(np.identity(4))

# [[1. 0. 0. 0.]

# [0. 1. 0. 0.]

# [0. 0. 1. 0.]

# [0. 0. 0. 1.]]

転置

行列の転置にはtranspose()メソッドを使う。代替として.Tとしてもよい。

m = np.array([[1, 2, 3], [4, 5, 6]])
print(m.transpose())
print(m.T)

# [[1 4]
#  [2 5]
#  [3 6]]
# [[1 4]
#  [2 5]
#  [3 6]]

m = np.array([[1, 2, 3], [4, 5, 6]])

print(m.transpose())

print(m.T)

# [[1 4]

# [2 5]

# [3 6]]

# [[1 4]

# [2 5]

# [3 6]]

一次元配列で定義したベクトルにはtranspose()は効かない。列ベクトルに変換するにはreshape()メソッドを使う（reshape(行数, 列数)）。

v = np.array([1, 2, 3])
print(v.T)
print(v.reshape(3, 1))

# [1 2 3]
# [[1]
#  [2]
#  [3]]

v = np.array([1, 2, 3])

print(v.T)

print(v.reshape(3, 1))

# [1 2 3]

# [[1]

# [2]

# [3]]

演算

定数倍

ベクトル・行列の定数倍は、各要素の定数倍。

a = 2
v = np.array([1, 2, 3])
m = np.array([[1, 2, 3], [4, 5, 6]])

print(a*v)
print(a*m)

# [2 4 6]
# [[ 2  4  6]
#  [ 8 10 12]]

a = 2

v = np.array([1, 2, 3])

m = np.array([[1, 2, 3], [4, 5, 6]])

print(a*v)

print(a*m)

# [2 4 6]

# [[ 2 4 6]

# [ 8 10 12]]

加減

同じ要素数のベクトル、同じ次元の行列同士の下限は要素同士の加減

a = np.array([1, 2, 3])
b = np.array([2, 4, 6])
A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 4], [6, 8]])

print(a + b)
print(a - b)
print(A + B)
print(A - B)

# [3 6 9]
# [-1 -2 -3]
# [[ 3  6]
#  [ 9 12]]
# [[-1 -2]
#  [-3 -4]]

a = np.array([1, 2, 3])

b = np.array([2, 4, 6])

A = np.array([[1, 2], [3, 4]])

B = np.array([[2, 4], [6, 8]])

print(a + b)

print(a - b)

print(A + B)

print(A - B)

# [3 6 9]

# [-1 -2 -3]

# [[ 3 6]

# [ 9 12]]

# [[-1 -2]

# [-3 -4]]

ベクトルの内積

同じ要素数のベクトルの内積（ドット積）はnp.dot()で計算。

$\begin{equation*} {\bf a} \cdot {\bf b} = \sum_{i=1}^n a_i b_i \end{equation*}$

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print(np.dot(a, b))

# 32

a = np.array([1, 2, 3])

b = np.array([4, 5, 6])

print(np.dot(a, b))

# 32

*演算子を使うと、要素ごとの積になる。

print(a*b)

# [ 4 10 18]

print(a*b)

# [ 4 10 18]

行列の積

行列同士の積もnp.dot()で計算。l×m行列とm×n行列の積はl×n行列になる。

$\begin{equation*} \left( \begin{array}{ccc} a_{11} & \cdots & a_{1m} \\ \vdots & a_{ij} & \vdots \\ a_{l1} & \cdots & a_{lm} \\ \end{array} \right) \cdot \left( \begin{array}{ccc} b_{11} & \cdots & b_{1n} \\ \vdots & b_{jk} & \vdots \\ b_{m1} & \cdots & b_{mn} \\ \end{array} \right) = \left( \sum_{j=1}^m a_{ij} b_{jk} \right) \end{equation*}$

A = np.array([[1, 2, 3],
              [4, 5, 6]])
B = np.array([[1, 2],
              [3, 4],
              [5, 6]])
print(np.dot(A, B))

# [[22 28]
#  [49 64]]

A = np.array([[1, 2, 3],

[4, 5, 6]])

B = np.array([[1, 2],

[3, 4],

[5, 6]])

print(np.dot(A, B))

# [[22 28]

# [49 64]]

次元数が整合しないとエラーになる。

A = np.array([[1, 2, 3],
              [4, 5, 6]])
B = np.array([[1, 2],
              [3, 4]])
print(np.dot(A, B))

# ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)

A = np.array([[1, 2, 3],

[4, 5, 6]])

B = np.array([[1, 2],

[3, 4]])

print(np.dot(A, B))

# ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)

行ベクトルと行列の積は、ベクトルを前からかけてok。

$\begin{equation*} (1, 2, 3) \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) = (30, 36, 42) \end{equation*}$

a = np.array([1, 2, 3])
A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])
print(np.dot(a, A))

# [30 36 42]

a = np.array([1, 2, 3])

A = np.array([[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.dot(a, A))

# [30 36 42]

行列と列ベクトルの積は、一次元配列のベクトルをreshape()で列ベクトルに変換してから。

$\begin{equation*} \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) \left( \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right) = \left( \begin{array}{c} 14 \\ 32 \\ 50 \end{array} \right) \end{equation*}$

A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])
a = np.array([1, 2, 3]).reshape(3, 1)
print(np.dot(A, a))

# [[14]
#  [32]
#  [50]]

A = np.array([[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

a = np.array([1, 2, 3]).reshape(3, 1)

print(np.dot(A, a))

# [[14]

# [32]

# [50]]

なお、np.dot()の代わりに演算子@が使える。ベクトル同士なら内積、少なくともいずれか一つが行列なら行列積。

a = np.array([1, 2])
b = np.array([1, 2, 3]).reshape(3, 1)
A = np.array([[1, 2, 3],
              [4, 5, 6]])
B = np.array([[1, 2],
              [3, 4],
              [5, 6]])
print(a @ a)
print(a @ A)
print(A @ b)
print(A @ B)

# 5
# [ 9 12 15]
# [[14]
#  [32]]
# [[22 28]
#  [49 64]]

a = np.array([1, 2])

b = np.array([1, 2, 3]).reshape(3, 1)

A = np.array([[1, 2, 3],

[4, 5, 6]])

B = np.array([[1, 2],

[3, 4],

[5, 6]])

print(a @ a)

print(a @ A)

print(A @ b)

print(A @ B)

# 5

# [ 9 12 15]

# [[14]

# [32]]

# [[22 28]

# [49 64]]

numpy.linalgパッケージ

行列式

行列式はnumpy.linalgパッケージのdet()関数で得られる。linalgは”linear algebra”の略で、慣例としてLAという名前で代替される。

import numpy.linalg as LA

A = np.array([[1, 2],
              [3, 4]])
B = np.array([[1, 2, 3],
              [2, 1, 3],
              [3, 1, 2]])

print(LA.det(A))
print(LA.det(B))

# -2.0000000000000004
# 6.000000000000001

import numpy.linalg as LA

A = np.array([[1, 2],

[3, 4]])

B = np.array([[1, 2, 3],

[2, 1, 3],

[3, 1, 2]])

print(LA.det(A))

print(LA.det(B))

# -2.0000000000000004

# 6.000000000000001

逆行列

逆行列はnumpy.linalgパッケージのinv()関数で得られる。

A = np.array([[1, 2],
              [3, 4]])
B = np.array([[1, 2, 3],
              [2, 1, 3],
              [3, 1, 2]])

print(LA.inv(A))
print(LA.inv(B))

# [[-2.   1. ]
#  [ 1.5 -0.5]]
# [[-0.16666667 -0.16666667  0.5       ]
#  [ 0.83333333 -1.16666667  0.5       ]
#  [-0.16666667  0.83333333 -0.5       ]]

A = np.array([[1, 2],

[3, 4]])

B = np.array([[1, 2, 3],

[2, 1, 3],

[3, 1, 2]])

print(LA.inv(A))

print(LA.inv(B))

# [[-2. 1. ]

# [ 1.5 -0.5]]

# [[-0.16666667 -0.16666667 0.5 ]

# [ 0.83333333 -1.16666667 0.5 ]

# [-0.16666667 0.83333333 -0.5 ]]

固有値・固有ベクトル

正方行列の固有値と固有ベクトルを、eig()関数で得ることができる(行列の固有値・固有ベクトルの例題を用いた)。

A = np.array([[3, 1],
              [2, 4]])
print(LA.eig(A))

# (array([2., 5.]), array([[-0.70710678, -0.4472136 ],
#        [ 0.70710678, -0.89442719]]))

A = np.array([[3, 1],

[2, 4]])

print(LA.eig(A))

# (array([2., 5.]), array([[-0.70710678, -0.4472136 ],

# [ 0.70710678, -0.89442719]]))

結果は固有値が並んだベクトルと固有ベクトルが並んだ配列で、それぞれを取り出して利用する。なお、固有ベクトルはノルムが1となるように正規化されている。

eigenvalues, eigenvectors = LA.eig(A)
print(eigenvalues)
print(eigenvectors)

# [2. 5.]
# [[-0.70710678 -0.4472136 ]
#  [ 0.70710678 -0.89442719]]

eigenvalues, eigenvectors = LA.eig(A)

print(eigenvalues)

print(eigenvectors)

# [2. 5.]

# [[-0.70710678 -0.4472136 ]

# [ 0.70710678 -0.89442719]]

注意が必要なのは固有ベクトルの方で、各固有ベクトルは配列の列ベクトルとして並んでいる。固有ベクトルを取り出す方法は2通り。

固有値に対応するサフィックスで列ベクトルを取り出す。この方法はnumpyの公式ドキュメントにも以下のように書かれている。

v(…, M, M) array: The normalized (unit “length”) eigenvectors, such that the column v[:,i] is the eigenvector corresponding to the eigenvalue w[i].

print(eigenvectors[:,0], eigenvectors[:,1])

# [-0.70710678  0.70710678] [-0.4472136  -0.89442719]

print(eigenvectors[:,0], eigenvectors[:,1])

# [-0.70710678 0.70710678] [-0.4472136 -0.89442719]

固有ベクトルの配列を転置して、行ベクトルの並びにする。

eigenvectors = eigenvectors.T
print(eigenvectors[0], eigenvectors[1])

# [-0.70710678 0.70710678] [-0.4472136 -0.89442719]

eigenvectors = eigenvectors.T

print(eigenvectors[0], eigenvectors[1])

# [-0.70710678 0.70710678] [-0.4472136 -0.89442719]

Python3 – numpy

2019-09-23 / tau / コメントする

全般

numpyのインストール

randomモジュール

基本機能

配列・ndarray

Tips

配列の応用

集計・確率・統計

各種関数

`where()関数`

Numpy.where()は、配列中の要素を検索してそのインデックスを得たり、配列の条件によって指定した配列から要素を選び出すことができる。

numpy – 統計量と組み込み関数の注意点

2019-09-22 / tau / コメントする

概要

Pythonのnumpyで統計量を扱う場合、分散・共分散で注意を要する点がある。Excelの関数でも同様だが、分散・共分散が標本値からそのまま計算した値か、不偏推定量として計算した値か、ということを意識する必要がある。

ここでは、ndarrayから律義に計算した値と、numpyの組み込み関数から計算した値を比較してみる。

標本数・総和・平均

標本として与えた配列の要素数、全要素の和、総和を要素数で除した値で、そのまま母集団の不偏推定量。

import numpy as np

x = np.array([1, 2, 3, 4, 5])
n = len(x)
sum_x = x.sum()
mean_x = sum_x / n
print(n)
print(sum_x)
print(mean_x, x.mean())

# 5
# 15
# 3.0 3.0

import numpy as np

x = np.array([1, 2, 3, 4, 5])

n = len(x)

sum_x = x.sum()

mean_x = sum_x / n

print(n)

print(sum_x)

print(mean_x, x.mean())

# 5

# 15

# 3.0 3.0

分散・標準偏差の食い違い

`var()`、`std()`は標本の分散・標準偏差

分散・共分散については、提供されたメソッドvar()、std()は標本数で除した標本分散・共分散となる。

x = np.array([1, 2, 3, 4, 5])
n = len(x)
var_x = np.sum((x - x.mean())**2) / n
std_x = np.sqrt(var_x)
print(var_x, x.var())
print(std_x, x.std())

# 2.0 2.0
# 1.4142135623730951 1.4142135623730951

x = np.array([1, 2, 3, 4, 5])

n = len(x)

var_x = np.sum((x - x.mean())**2) / n

std_x = np.sqrt(var_x)

print(var_x, x.var())

print(std_x, x.std())

# 2.0 2.0

# 1.4142135623730951 1.4142135623730951

不偏分散やその平方根を求める場合は、var()、std()の引数でddof=1とする。

`cov()`で与えられるのは不偏推定量

numpy.cov()で二つの一次元配列の分散・共分散行列を得ることができる。分散共分散行列は

$\begin{equation*} \left[ \begin{array}{ll} {\rm Var}(X) & {\rm Cov}(XY) \\ {\rm Cov}(XY) & {\rm Var}(Y) \end{array} \right] \end{equation*}$

で定義されるが、以下の計算結果の対角要素は、先の分散の計算結果(2.0)と異なっている。

x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 2, 3, 4, 5])
print(np.cov(x, y))

# [[2.5 2.5]
#  [2.5 2.5]]

x = np.array([1, 2, 3, 4, 5])

y = np.array([1, 2, 3, 4, 5])

print(np.cov(x, y))

# [[2.5 2.5]

# [2.5 2.5]]

これらの値は、分散を標本分散ではなく不偏推定量で計算しているためで、試しに先の計算を不偏分散で計算してみると結果は整合する。

ちなみに標本分散は偏差の二乗和を標本数nで割り、不偏分散はn-1で割る。

x = np.array([1, 2, 3, 4, 5])
n = len(x)
var_x = np.sum((x - x.mean())**2) / (n - 1)
print(var_x)

# 2.5

x = np.array([1, 2, 3, 4, 5])

n = len(x)

var_x = np.sum((x - x.mean())**2) / (n - 1)

print(var_x)

# 2.5

共分散にも注意

上記では分散について確認したが、共分散についても注意が必要。

共分散は一般に以下で定義される。

$\begin{equation*} {\rm Cov}(X, Y) = E((X - \overline{X}) (Y - \overline{Y})) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \overline{x}) (y_i - \overline{y}) \end{equation*}$

これに従って計算した結果。

x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 2, 3, 4, 5])
n = len(x)
cov_xy = np.sum((x - x.mean())*(y - y.mean())) / n
print(cov_xy)

# 2.0

x = np.array([1, 2, 3, 4, 5])

y = np.array([1, 2, 3, 4, 5])

n = len(x)

cov_xy = np.sum((x - x.mean())*(y - y.mean())) / n

print(cov_xy)

# 2.0

この結果は、numpy.cov()で計算した非対角要素2.5と食い違う。

ここでn→n-1として計算しなおすと結果は2.5となり同じ値となる。

共分散用は、たとえば回帰分析の残差変動を計算するときに利用するが、その時には標本の共分散を使うので、注意が必要。

numpyで統計計算をする際、特に共分散については、律義に定義式から計算するのがよさそう。

numpy – 配列の統計計算（二次元配列）

2019-09-22 / tau / コメントする

概要

二次元配列についても、一次元配列と同様な統計関係のメソッド群がある。

二次元についても、同じ機能のメソッドがnumpy、ndarrayのメソッドとして準備されている。

二次元配列の場合は、最小・総和・平均などの計算を全要素／列単位／行単位のいずれで行うかを区別する。具体例として、以下の3×3配列の最小値min()を全要素、列単位、行単位で計算した例を示す。

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(np.min(m))
print(np.min(m, axis=0))
print(np.min(m, axis=1))

# 1
# [1 2 3]
# [1 4 7]

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(np.min(m))

print(np.min(m, axis=0))

print(np.min(m, axis=1))

# 1

# [1 2 3]

# [1 4 7]

引数axisを指定しないと全要素が対象となり、axis=0を指定すると列ごとの計算結果を一次元の配列に、axis=1を指定すると行ごとの計算結果を一次元の配列にして返す。

axis=1の場合、計算は行ごとに行われるが、結果は列ベクトルではなく行ベクトルの配列となる。

また、numpyのメソッドではなくndarrayのメソッドでも同じように使える。

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(m.min())
print(m.min(axis=0))
print(m.min(axis=1))

# 1
# [1 2 3]
# [1 4 7]

m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

print(m.min())

print(m.min(axis=0))

print(m.min(axis=1))

# 1

# [1 2 3]

# [1 4 7]

最小値・最大値

最小値／最大値を返す。

numpy.min(m, axis=0/1)
numpy.max(m, axis=0/1)
m.min(axis=0/1)
m.max(axis=0/1)

結果は同じなので、numpyのメソッドについて実行例を示す。

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.min(m))         # 1
print(np.min(m, axis=0)) # [1 2 3]
print(np.min(m, axis=1)) # [1 4 7]
print(np.max(m))         # 9
print(np.max(m, axis=0)) # [7 8 9]
print(np.max(m, axis=1)) # [3 6 9]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.min(m)) # 1

print(np.min(m, axis=0)) # [1 2 3]

print(np.min(m, axis=1)) # [1 4 7]

print(np.max(m)) # 9

print(np.max(m, axis=0)) # [7 8 9]

print(np.max(m, axis=1)) # [3 6 9]

総和・総積

一次元配列の全要素の和・積を返す。

numpy.sum(m, axis=0/1)
numpy.prod(m, axis=0/1)
m.sum(axis=0/1)
m.prod(axis=0/1)

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.sum(m))          # 45
print(np.sum(m, axis=0))  # [12 15 18]
print(np.sum(m, axis=1))  # [ 6 15 24]
print(np.prod(m))         # 362880
print(np.prod(m, axis=0)) # [ 28  80 162]
print(np.prod(m, axis=1)) # [  6 120 504]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.sum(m)) # 45

print(np.sum(m, axis=0)) # [12 15 18]

print(np.sum(m, axis=1)) # [ 6 15 24]

print(np.prod(m)) # 362880

print(np.prod(m, axis=0)) # [ 28 80 162]

print(np.prod(m, axis=1)) # [ 6 120 504]

平均・分散・標準偏差

一次元配列の要素の平均、分散、標準偏差を返す。分散は標本分散なので、不偏分散が必要な場合はvar()*n/(n-1)とする（ただしn=len(v)）。

numpy.mean(m, axis=0/1)
numpy.var(m, axis=0/1)
numpy.std(m, axis=0/1)
m.mean(axis=0/1)
m.var(axis=0/1)
m.std(axis=0/1)

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.mean(m))         # 5.0
print(np.mean(m, axis=0)) # [4. 5. 6.]
print(np.mean(m, axis=1)) # [2. 5. 8.]
print(np.var(m))          # 6.666666666666667
print(np.var(m, axis=0))  # [6. 6. 6.]
print(np.var(m, axis=1))  # [0.66666667 0.66666667 0.66666667]
print(np.std(m))          # 2.581988897471611
print(np.std(m, axis=0))  # [2.44948974 2.44948974 2.44948974]
print(np.std(m, axis=1))  # [0.81649658 0.81649658 0.81649658]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.mean(m)) # 5.0

print(np.mean(m, axis=0)) # [4. 5. 6.]

print(np.mean(m, axis=1)) # [2. 5. 8.]

print(np.var(m)) # 6.666666666666667

print(np.var(m, axis=0)) # [6. 6. 6.]

print(np.var(m, axis=1)) # [0.66666667 0.66666667 0.66666667]

print(np.std(m)) # 2.581988897471611

print(np.std(m, axis=0)) # [2.44948974 2.44948974 2.44948974]

print(np.std(m, axis=1)) # [0.81649658 0.81649658 0.81649658]

累積和・累積積

一次元配列の要素について先頭から累積して積・和を計算し、それらを要素とする配列を返す。

二次元配列でaxis=0を指定した場合、列ごとに行方向に累積した値が並べられた二次元配列となり、axis=1を指定した場合は行ごとに列方向に累積した値が並べられた二次元配列となる。

numpy.cumsum(m)
numpy.cumprod(m)
m.cumsum()
m.cumprod()

m = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])
print(np.cumsum(m))
print(np.cumsum(m, axis=0))
print(np.cumsum(m, axis=1))
print(np.cumprod(m))
print(np.cumprod(m, axis=0))
print(np.cumprod(m, axis=1))

# [ 1  3  6 10 15 21 28 36 45]
# [[ 1  2  3]
#  [ 5  7  9]
#  [12 15 18]]
# [[ 1  3  6]
#  [ 4  9 15]
#  [ 7 15 24]]

# [     1      2      6     24    120    720   5040  40320 362880]
# [[  1   2   3]
#  [  4  10  18]
#  [ 28  80 162]]
# [[  1   2   6]
#  [  4  20 120]
#  [  7  56 504]]

m = np.array([

[1, 2, 3],

[4, 5, 6],

[7, 8, 9]])

print(np.cumsum(m))

print(np.cumsum(m, axis=0))

print(np.cumsum(m, axis=1))

print(np.cumprod(m))

print(np.cumprod(m, axis=0))

print(np.cumprod(m, axis=1))

# [ 1 3 6 10 15 21 28 36 45]

# [[ 1 2 3]

# [ 5 7 9]

# [12 15 18]]

# [[ 1 3 6]

# [ 4 9 15]

# [ 7 15 24]]

# [ 1 2 6 24 120 720 5040 40320 362880]

# [[ 1 2 3]

# [ 4 10 18]

# [ 28 80 162]]

# [[ 1 2 6]

# [ 4 20 120]

# [ 7 56 504]]

numpy – 配列の統計計算（一次元配列）

2019-09-22 / tau / コメントする

概要

一次元配列について、様々な統計関係の計算をするメソッド群。

同じ機能のメソッドがnumpy、ndarrayのメソッドとして準備されている。例えば一次元配列vについて最小値を求めるメソッドは、numpy.min(v)とv.min()のいずれも同じ結果を返す。

最小値・最大値

一次元配列の要素のうち最小値／最大値を返す。

numpy.min(v)
numpy.max(v)
v.min()
v.max()

結果は同じなので、numpyのメソッドについて実行例を示す。

v = np.array([1, 2, 3, 4])
print(np.min(v))
print(np.max(v))

# 1
# 4

v = np.array([1, 2, 3, 4])

print(np.min(v))

print(np.max(v))

# 1

# 4

総和・総積

一次元配列の全要素の和・積を返す。

numpy.sum(v)
numpy.prod(v)
v.sum()
v.prod()

v = np.array([1, 2, 3, 4])
print(np.sum(v))
print(np.prod(v))

# 10
# 24

v = np.array([1, 2, 3, 4])

print(np.sum(v))

print(np.prod(v))

# 10

# 24

平均・分散・標準偏差

一次元配列の要素の平均、分散、標準偏差を返す。分散は標本分散なので、不偏分散が必要な場合はvar()*n/(n-1)とする（ただしn=len(v)）。

numpy.mean(v)
numpy.var(v)
numpy.std(v)
v.mean()
v.var()
v.std()

v = np.array([1, 2, 3, 4])
print(np.mean(v))
print(np.var(v))
print(np.std(v))

# 2.5
# 1.25
# 1.118033988749895

v = np.array([1, 2, 3, 4])

print(np.mean(v))

print(np.var(v))

print(np.std(v))

# 2.5

# 1.25

# 1.118033988749895

$\begin{eqnarray*} \overline{V} &=& \frac{1 + 2 + 3 + 4}{4} = 2.5 \\ {\rm Var}(V) &=& \frac{(1-2.5)^2+(2-2.5)^2+(3-2.5)^2+(4-2.5)^2}{4} \\ &=& \frac{2.25+0.25+0.25+2.25}{4} = \frac{5}{4} \\ &=& 1.25 \\ \sigma_V &=& \sqrt{1.25} = 1.1180 \ldots \end{eqnarray*}$

累積和・累積積

一次元配列の要素について先頭から累積して積・和を計算し、それらを要素とする配列を返す。

numpy.cumsum(v)
numpy.cumprod(v)
v.cumsum()
v.cumprod()

v = np.array([1, 2, 3, 4])
print(np.cumsum(v))
print(np.cumprod(v))

# [ 1  3  6 10]
# [ 1  2  6 24]

概要

全コード

利用方法

クラスタリングを行うインスタンスの生成

クラスタリングの実行

実行例

クラス説明

__init__()～インスタンス生成

get_result()～分析の実行

プライベートメソッド

_distance()～2点間の距離

_point_converged()～収束判定

_all_points_converged()～全ての点の収束判定

_set_nearest_mean_point()～各点に最も近い代表点

_revise_mean_points()～代表点の更新

random_scatter_data.py

概要

リストの場合

行の追加

append()メソッド

insert()メソッド

列の追加

append()メソッド

insert()メソッド

ndarrayの場合

行の追加

numpy.append()関数

numpy.insert()関数

numpy.vstack()関数

列の追加

numpy.append()関数

numpy.insert()関数

numpy.hstack()関数

概要

特定要素の取り出し

行の取り出し

列の取り出し

内包表記による列指定

1次元配列

要素の挿入

要素の追加

numpy.append()

numpy.insert()

numpy.hstack()

2次元配列

行の挿入・追加

列の挿入・追加

導入

逆行列による方法

numpy.linalg.solve()による方法

非正則行列の場合

ベクトルと行列の定義

リテラル

単位行列

転置

演算

定数倍

加減

ベクトルの内積

行列の積

numpy.linalgパッケージ

行列式

逆行列

固有値・固有ベクトル

全般

基本機能

配列・ndarray

集計・確率・統計

各種関数

where()関数

概要

標本数・総和・平均

分散・標準偏差の食い違い

var()、std()は標本の分散・標準偏差

cov()で与えられるのは不偏推定量

共分散にも注意

概要

最小値・最大値

総和・総積

平均・分散・標準偏差

`init()`～インスタンス生成

`get_result()`～分析の実行

`_distance()`～2点間の距離

`_point_converged()`～収束判定

`_all_points_converged()`～全ての点の収束判定

`_set_nearest_mean_point()`～各点に最も近い代表点

`_revise_mean_points()`～代表点の更新

`append()`メソッド

`insert()`メソッド

`append()`メソッド

`insert()`メソッド

`ndarray`の場合

`numpy.append()`関数

`numpy.insert()`関数

`numpy.vstack()`関数

`numpy.append()`関数

`numpy.insert()`関数

`numpy.hstack()`関数

`numpy.append()`

`numpy.insert()`

`numpy.hstack()`

`where()関数`

`var()`、`std()`は標本の分散・標準偏差

`cov()`で与えられるのは不偏推定量